Measurement of Interfacial Tension between Liquid Pb and a Molten LiCl-NaCl-KCl Mixture via a Floating Drop Method
Abstract
:1. Introduction
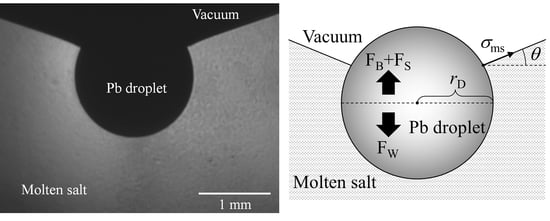
2. Determination of Interfacial Tension
3. Experiment
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bera, A.; Ojha, K.; Mandal, A.; Kumar, T. Interfacial tension and phase behavior of surfactant-brine–oil system. Colloids Surf. A Physicochem. Eng. Asp. 2011, 383, 114–119. [Google Scholar] [CrossRef]
- Cong, Y.; Zhang, W.; Liu, C.; Huang, F. Composition and Oil-Water Interfacial Tension Studies in Different Vegetable Oils. Food Biophys. 2020, 15, 229–239. [Google Scholar] [CrossRef]
- Ogino, K. Chemistry of Interface at High Temperatures; AGNE Gijutsu Center Inc.: Tokyo, Japan, 2008; Volume 1. [Google Scholar]
- Nakamoto, M.; Tanaka, T.; Yamamoto, T. Measurement of Interfacial Tension Based on a Floating Droplet Profile on a Liquid. In Proceedings of the 6th International Symposium on Advanced Science Technology In Experiment Mechanics (ISEM 2011), Osaka, Japan, 5 November 2011. [Google Scholar]
- Nakamoto, M.; Tanaka, T.; Yamamoto, T. Measurement of interfacial tension between oil and an aqueous solution via a floating drop method. Colloids Surf. A Physicochem. Eng. Asp. 2017, 529, 985–989. [Google Scholar] [CrossRef]
- Nakamoto, M.; Kasai, Y.; Tanaka, T.; Yamamoto, T. Measurement of liquid/liquid interfacial tension with water on liquid paraffin by the floating drop method. Colloids Surf. A Physicochem. Eng. Asp. 2020, 603, 125250. [Google Scholar] [CrossRef]
- Han, Z.; Holappa, L. Characteristics of Iron Entrainment into Slag Due to Rising Gas Bubbles. ISIJ Int. 2003, 43, 1698–1704. [Google Scholar] [CrossRef]
- Taniguchi, Y.; Seethraman, S. Interfacial Phenomena among Liquid Iron-Carbon Alloy, Liquid Slag, and Solid CaO. Metall. Trans. B 2012, 43, 587–597. [Google Scholar] [CrossRef]
- Terashima, H.; Nakamura, T.; Noguchi, F.; Ueda, Y. Floating Behavior of Molten Copper and Copper Matte Drops on Slag Surface—Study on interfacial phenomena in phase separation of copper smelting (3rd Report). J. Min. Metall. Inst. Jpn. 1990, 106, 881–885. [Google Scholar] [CrossRef] [Green Version]
- Utigard, T.; Toguri, J.M.; Nakamura, T. Interfacial Tension and Flotation Characteristics of Liquid Metal-Sodium Flux Systems. Metall. Trans. B 1986, 17, 339–346. [Google Scholar] [CrossRef]
- Poggi, D.; Minto, R.; Davenport, W.G. Mechanisms of Metal Entrapment in Slags. J. Met. 1969, 21, 40–45. [Google Scholar] [CrossRef]
- Ishii, K.; Kitamura, S.; Shibata, H.; Maruoka, N.; Song, D.-Y. Measurement of interfacial tension between Pb/Al-Cu alloy and molten KCl-LiCl-NaCl salt. In Proceedings of the 32nd Japan Symposium on Thermophysical Properties, Yokohama, Japan, 21–23 November 2011. [Google Scholar]
- Lin, P.-L.; Pelton, A.D.; Bale, C.W. Computation of Ternary Molten Salt Phase Diagrams. J. Am. Ceram. Soc. 1979, 62, 414–422. [Google Scholar] [CrossRef]
- Krylov, A.S.; Vvedensky, A.V.; Katsnelson, A.M.; Tugovikov, A.E. Software package for determination of surface tension of liquid metals. Non-Cryst. Solids 1993, 156–158, 845–848. [Google Scholar] [CrossRef]
- Iida, T.; Guthrie, R.I.L. The Physical Properties of Liquid Metals; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- NIST Molten Salt Database; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1987.
- Ooi, C.H.; Plackowski, C.; Nguyen, A.V.; Vadivelu, R.K.; St. John, J.A.; Dao, D.V.; Nguyen, N.-T. Floating mechanism of a small liquid marble. Sci. Rep. 2016, 6, 21777. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanaka, T.; Kitamura, T.; Back, I.A. Evaluation of Surface Tension of Molten Ionic Mixtures. ISIJ Int. 2006, 46, 400–406. [Google Scholar] [CrossRef] [Green Version]
- Nakamoto, M.; Kiyose, A.; Tanaka, T.; Holappa, L.; Hämäläinen, M. Evaluation of the Surface Tension of Ternary Silicate Melts Containing Al2O3, CaO, FeO, MgO or MnO. ISIJ Int. 2007, 47, 38–43. [Google Scholar] [CrossRef] [Green Version]
- Nakamoto, M.; Tanaka, T.; Holappa, L.; Hämäläinen, M. Surface Tension Evaluation of Molten Silicates Containing Surface-active Components (B2O3, CaF2 or Na2O). ISIJ Int. 2007, 47, 211–216. [Google Scholar] [CrossRef] [Green Version]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]







| Substance | Density (g/cm3) | Surface Tension (mN/m) |
|---|---|---|
| LiCl | 1.8842–4.3280 × 10−4T | 187.6507–0.0617810T |
| NaCl | 2.1390–5.444 × 10−4T | 187.0–0.068T |
| KCl | 2.1359–5.831 × 10−4T | 176.8–0.075T |
| Li+ | 0.68 |
| Na+ | 0.97 |
| K+ | 1.33 |
| Cl− | 1.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakamoto, M.; Tanaka, T.; Yamamoto, T. Measurement of Interfacial Tension between Liquid Pb and a Molten LiCl-NaCl-KCl Mixture via a Floating Drop Method. Metals 2022, 12, 1198. https://doi.org/10.3390/met12071198
Nakamoto M, Tanaka T, Yamamoto T. Measurement of Interfacial Tension between Liquid Pb and a Molten LiCl-NaCl-KCl Mixture via a Floating Drop Method. Metals. 2022; 12(7):1198. https://doi.org/10.3390/met12071198
Chicago/Turabian StyleNakamoto, Masashi, Toshihiro Tanaka, and Takaiku Yamamoto. 2022. "Measurement of Interfacial Tension between Liquid Pb and a Molten LiCl-NaCl-KCl Mixture via a Floating Drop Method" Metals 12, no. 7: 1198. https://doi.org/10.3390/met12071198
APA StyleNakamoto, M., Tanaka, T., & Yamamoto, T. (2022). Measurement of Interfacial Tension between Liquid Pb and a Molten LiCl-NaCl-KCl Mixture via a Floating Drop Method. Metals, 12(7), 1198. https://doi.org/10.3390/met12071198