4. Discussion
This paper was mainly aimed to investigate the effects of different microchemistries (constituents, solid solution levels and dispersoids) on the substructure evolution during rolling to different strains and the subsequent softening behavior during back-annealing. Particular focus has been given to the influence of different dispersoid structures, whether pre-existing or mainly formed during back-annealing, in terms of the number density and size, on softening kinetics and final recrystallized grain size.
At low to medium temperatures of homogenization, the precipitation of dispersoids is controlled by nucleation and growth due to the relatively low diffusion rate of Mn in Al. At a homogenization temperature of 450 °C, the number density of dispersoids can reach a maximum and the spatial distance of dispersoids reaches a minimum. When increasing the temperature further, the diffusion speed of Mn in the matrix is increased significantly, and for annealing at 600 °C, dissolution of small and coarsening of large dispersoids as well as constituent particles becomes the prominent process due to the increased solubility and the fact that long distance diffusion becomes possible. This explains the difference in solid solution level and dispersoid structures of the two conditions C2-1 and C2-2. The slow and elaborate cooling procedure of condition C2-3 ensures additional precipitation of Mn into constituents and dispersoids while preserving a fairly coarse dispersoid structure and bringing the solid solution level even below the one in C2-2 (
cf. Table 1).
In terms of constituents both the C2-1 and C2-3 conditions contain fewer and larger particles, than the non-homogenized condition, due to coarsening during homogenization. The C2-2 material, which was homogenized at a relatively low holding temperature (450 °C), contains smaller, but considerably more particles, due to less coarsening. Moreover, in the C2-2 material the constituent particles are mainly thin plates which can break up more easily during deformation, which increases the number density and decreases the size of constituent particles during rolling. On the other side, both C2-1 and C2-3 contains more particles with sizes larger than 1 µm, which is typically a critical size for successful PSN in aluminum alloys. The microchemistry states observed here are in accordance with earlier work on the evolution of particles during homogenization of similar alloys [
26,
27].
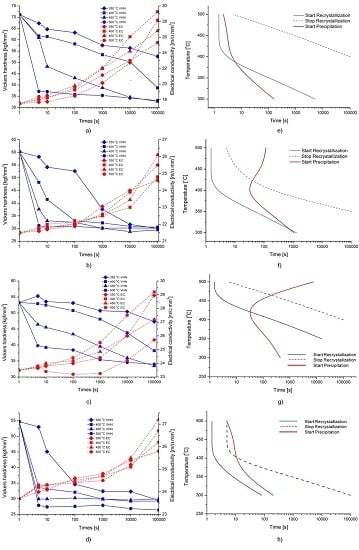
The present work has clearly confirmed that the different microchemistries following the different homogenization procedures have a profound effect on the back-annealing behavior, in line with previous findings in similar alloys (e.g., [
13,
18,
19,
20]). Generally, conditions which are mainly unaffected by dispersoid effects give a fairly fine grained structure. This applies for conditions without dispersoids or when the dispersoids are coarse and/or with a low number density and in condition with no or limited concurrent precipitation. Faster kinetics and slightly refined grain structures are generally obtained with increased annealing temperature and a larger cold rolling strain. On the other hand, in conditions with either a considerable density of fine pre-existing dispersoids and/or significant concurrent precipitation of fine dispersoids, the influence can be quite pronounced with much slower kinetics and strongly modified, generally much coarser, grain structures. In some cases of low stored energy and/or low annealing temperatures recrystallization can be completely prevented and only extended recovery takes place. Although only indicative with respect to start and stop of precipitation and recrystallization, respectively, the respective TTT-diagrams are quite useful in discussing the interaction of these two reactions and in particular the influence of concurrent precipitation on the recrystallization behavior. Nonetheless, the present work have also shown that a high density of fine dispersoids whether pre-existing or formed during annealing (concurrent precipitation), both have a strong and comparable effect on kinetics and recrystallized microstructure, the latter in the form of large and highly elongated grains. The recrystallization textures for most of the conditions considered here have been reported elsewhere [
18,
19,
20]. In the absence of dispersoids the texture is found to be generally weak, indicating that PSN plays a prominent role as nucleation mechanism for recrystallization in these alloys. In the presence of dispersoids, on the other, the textures become dominated by a distinct P-texture and a ND-rotated cube component [
13,
14,
18,
19,
20]. The two latter are also generally associated with large particles, which indicates that PSN also plays a dominant role in these conditions.
The effect of rolling strain, increasing from ε = 1.6 to 3.0, on the softening behavior, is in general much less pronounced than the microchemistry effects. Higher strain gives a higher stored energy (and thus larger driving force) for recrystallization, consistent with slightly higher as-deformed hardness at the higher strain (compare
Figure 6a–d and
Figure S1). Accordingly the kinetics is consistently faster for all material conditions. In principle this should also promote nucleation of recrystallization, and then a smaller grain size, which is not obvious from the present experimental results (
cf. Table 5), where even some counter-intuitive results are observed with increasing grain size with increasing strain. As mentioned above these results may be the result of different concurrent precipitation behavior and/or an artifact due to poor statistics/measurement uncertainties in the measured results. Moreover, the directional homogeneities introduced by the rolling process where characteristic length scales (between e.g., dispersoid layers and constituents (PSN sites) are shortened along ND and extended along RD with increasing strain may also play a role.
Although the shape effect discussed above cannot be completely accounted for, a rough estimate of grain size in selected cases can now be made, assuming PSN to be the dominating nucleation mechanism for recrystallization for all conditions. In doing so we make use of ideas from the ALSOFT model [
29], and the available experimental data for the deformation sub-structure, constituent particles and dispersoids (
cf. Table 3,
Table 4 and
Table 6). Following Vatne
et al. [
29], it is assumed that the critical step for nucleation from large constituent particles is growth out the deformation zone around these particles,
i.e., the critical particle size for a successful PSN event is given by the Gibbs-Thompson equation,
i.e., η* = 4γ
GB/
Peff where γ
GB is the particle-matrix interfacial energy between the nucleus and the deformed aluminum matrix. Here, it is assumed that the size of the deformation zone scales with the size of the particle itself.
The quantity
Peff is effective driving force for recrystallization and is given by the following expression:
Here,
PD is the driving pressure for recrystallization/stored energy in terms of sub-grain size δ (mean diameter) and the cell interior dislocation density ρ
i.
PZ (last term in Equation (2)) is the Zener pinning pressure due to a particle volume fraction
Fv of radius
r [
4,
15], and γ
SB and γ
GB are the boundary energies for sub-grains and high angle grain boundaries, respectively.
G is shear modulus and
b is Burgers vector. It should be noted that the Zener-pressure expression in Equation (2) is based on the assumption of spherical equi-axed particles with a random spatial distribution. The latter assumption is generally not valid in our case, as the dispersoids tend to be located at the grain boundaries where they may more effectively pin the boundaries (a higher effective Zener drag [
2,
4,
10,
31]). However, for qualitative purposes Equation (2) may still be used.
Making use of Equation (1) for the size distribution of constituent particles, the following relationship for the number density of PSN nuclei can then be derived [
29]:
where
N0 and
L are defined from Equation (1)
f, and
CPSN and
CPE are model constants of the order ~1. On the assumption that site-saturation nucleation kinetics applies, the recrystallized grain size then becomes:
In estimating
PD and
PZ, respectively, according to Equation (2), we use γ
GB = 0.3 Jm
−2 [
32] and
= 0.15 Jm
−2 (assuming an average misorientation angle of θ~4° and θ
c~15°),
G = 26.5 GPa,
b = 2.86 Å together with relevant data from
Table 4 and
Table 6 with
, where
d3D is the equivalent spherical particle diameter (3D) derived from the mean cross sectional diameter in
Table 6. Moreover the equivalent circle diameter (CED) is used for the sub-grain size. Following [
32], the contribution from cell interior dislocations can be ignored as it represents only a small contribution to the stored energy at the onset of recrystallization (typically 1%–2% [
32]). The results are presented in
Table 7, where values marked with an asterisk refer to artificially changed input parameter values to highlight how the stored energy and the Zener drag may influence the result.
Ignoring the shape effect and that some of the experimentally measured grain sizes are counter-intuitive (in view of the strain dependence), the calculated results are grossly in agreement with the experimental results (
cf. Table 5). This result supports the assumption of PSN being the dominant nucleation mechanism. For the C2-3 alloy the results actually compares quite well with the experiments, although the variation with strain is not consistent with the experiments. For some conditions a better agreement, is obtained by changing either the stored energy or the Zener drag values (data marked with *). Concerning the stored energy, the results clearly indicate that for some conditions the stored energy is underestimated,
i.e., the respective measured sub-grain size is too large and/or neglecting the dislocation contribution may have contributed to the underestimation in these cases. Especially for the C2-1 alloy this seems reasonable as the measured sub-grain size seems somewhat high. The indicated underestimations of the Zener drag is supported by more recent comprehensive model predictions with the ALSOFT model [
33]. Both for the C2-0 alloy after a strain of ε = 3, and the C2-2 material, the grain sizes obtained with nominal input for the Zener drag, is much too low, indicating that the actual Zener drag effect on nucleation (determining the grain size), as estimated from the classical Zener expression, Equation (3), is much too low. In fact, increasing the nominal Zener drag with a factor of 2, gives results which are more in line with the experiments. It should also be noted that the actual Zener drag also increases during annealing, due to (additional) concurrent precipitation (
cf. Table 6; [
18]). With a long incubation for onset of recrystallization (possible slow time-dependent nucleation), and possibly also boundary-dispersoid correlations the increased Zener drag may actually be closer to reality, also during nucleation, than the lower nominal one.