Residual Stresses with Time-Independent Cyclic Plasticity in Finite Element Analysis of Welded Joints
Abstract
:1. Introduction
2. Generation of Residual Stresses in Welded Joints
3. Time-Independent Cyclic Plasticity: The Chaboche Model
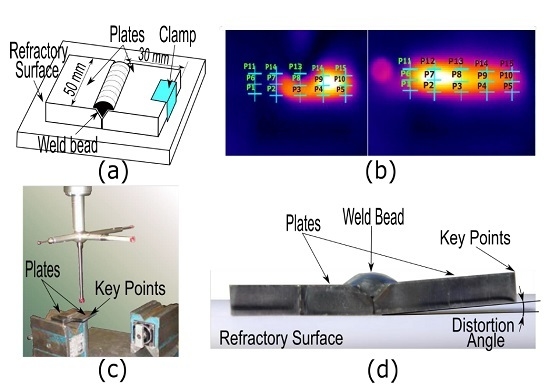
4. Manufacturing Procedure and Welding Configuration
5. Temperature Field, Angular Distortion, and Residual Stress Measurement
6. FE Model Proposed
6.1. The Proposed Thermal FE Model
6.2. Angular Distortion and Residual Stresses of the Proposed FE Model
7. Results
7.1. Results Obtained from the Thermal Field
7.2. Results of the Angular Distortion and Residual Stresses
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Radaj, D. Heat Effects of Welding: Temperature Field, Residual Stress, Distortion, 1st ed.; Springer: Heidelberg/Berlin, Germany, 1992. [Google Scholar]
- Radaj, D. Welding Residual Stresses and Distortion: Calculation and Measurement, 1st ed.; DVS-Verlag: Dusseldorf, Germany, 2003. [Google Scholar]
- Macherauch, E.; Kloos, K.H. Origin, measurements and evaluation of residual stresses. In Residual Stress in Science and Technology, 1st ed.; DGM Verlag: Oberursel, Germany, 1987. [Google Scholar]
- Totten, G.E.; Howes, M.; Inoue, T. Handbook of Residual Stress and Deformation of Steel, 1st ed.; ASM International: Kinsman Road, OH, USA, 2002. [Google Scholar]
- Zambon, A.; Ferro, P.; Bonollo, F. Microstructural, compositional and residual stress evaluation of CO2 laser welded superaustenitic AISI 904L stainless steel. Mater. Sci. Eng. A Struct. 2006, 424, 117–127. [Google Scholar] [CrossRef]
- Thibault, D.; Bocher, P.; Thomas, M.; Gharghouri, M.; Côté, M. Residual stress characterization in low transformation temperature 13%Cr–4%Ni stainless steel weld by neutron diffraction and the contour method. Mater. Sci. Eng. A Struct. 2010, 527, 6205–6210. [Google Scholar] [CrossRef]
- Paradowska, A.; Price, J.W.H.; Ibrahim, R.; Finlayson, T. A neutron diffraction study of residual stress due to welding. J. Mater. Process. Technol. 2005, 164–165, 1099–1105. [Google Scholar] [CrossRef]
- Olabi, A.G.; Hashmi, M.S.J. Effects of the stress-relief conditions on a martensite stainless-steel welded component. J. Mater. Process Technol. 1998, 77, 216–225. [Google Scholar] [CrossRef]
- Lostado, R.; Escribano, R.; Martínez, M.Á.; Múgica, R. Improvement in the Design of Welded Joints of EN 235JR Low Carbon Steel by Multiple Response Surface Methodology. Metals 2016, 6, 205. [Google Scholar] [CrossRef]
- Berge, S. On the effect of plate thickness in fatigue of welds. Eng. Fract. Mech. 1985, 21, 423–435. [Google Scholar] [CrossRef]
- Ferreira, J.M.; Branco, C.M. Influence of the radius of curvature at the weld toe in the fatigue strength of fillet welded joints. Int. J. Fatigue 1989, 11, 29–36. [Google Scholar]
- Teng, T.L.; Fung, C.P.; Chang, P.H. Effect of weld geometry and residual stresses on fatigue in butt-welded joints. Int. J. Press. Vessels Pip. 2002, 79, 467–482. [Google Scholar] [CrossRef]
- Citarella, R.; Carlone, P.; Sepe, R.; Lepore, M. DBEM crack propagation in friction stir welded aluminum joints. Adv. Eng. Softw. 2016, 101, 50–59. [Google Scholar] [CrossRef]
- Citarella, R.; Carlone, P.; Lepore, M.; Sepe, R. Hybrid technique to assess the fatigue performance of multiple cracked FSW joints. Eng. Fract. Mech. 2016, 162, 38–50. [Google Scholar] [CrossRef]
- Carlone, P.; Citarella, R.; Sonne, M.R.; Hattel, J.H. Multiple crack growth prediction in AA2024-T3 friction stir welded joints, including manufacturing effects. Int. J. Fatigue 2016, 90, 69–77. [Google Scholar] [CrossRef]
- Lostado, R.; Fernandez, R.; Mac Donald, B.J.; Villanueva, P.M. Combining soft computing techniques and the finite element method to design and optimize complex welded products. Integr. Comput.-Aided Eng. 2015, 22, 153–170. [Google Scholar]
- Chaboche, J.L. Time-independent constitutive theories for cyclic plasticity. Int. J. Plast. 1986, 2, 149–188. [Google Scholar] [CrossRef]
- Lostado, R.; Martínez-de-Pisón, F.J.; Fernández, R.; Fernández, J. Using genetic algorithms to optimize the material behaviour model in finite element models of processes with cyclic loads. J. Strain Anal. Eng. 2011, 46, 143–159. [Google Scholar] [CrossRef]
- Mandal, N.K.; Dhanasekar, M. Sub-modelling for the ratchetting failure of insulated rail joints. Int. J. Mech. Sci. 2013, 75, 110–122. [Google Scholar] [CrossRef]
- Chatti, S.; Chtioui, N. Sheet metal forming simulation using finite elastoplasticity with mixed isotropic/kinematic hardening. Eur. J. Comput. Mech. 2011, 20, 427–453. [Google Scholar] [CrossRef]
- Pilipenko, A. Computer Simulation of Residual Stress and Distortion of Thick Plates in Multielectrode Submerged Arc Welding: Their Mitigation Techniques. Ph.D. Thesis, Department of Machine Design and Materials Technology Norwegian University of Science and Technology Trondheim, Trondheim, Norway, 2001. [Google Scholar]
- Goldak, J.A.; Akhlaghi, M. Computational Welding Mechanics, 1st ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Armstrong, P.J.; Frederick, C.O. A Mathematical Representation of the Multiaxial Bauschinger Effect; Central Electricity Generating Board and Berkeley Nuclear Laboratories, Research & Development Department: Berkely, UK, 1966. [Google Scholar]
- Petersson, N.; Popov, E.P. Constitutive relations for generalized loadings. J. Eng. Mech. Div. 1977, 103, 611–627. [Google Scholar]
- Krieg, R.D. A practical two surface plasticity theory. Acta Mech. 1975, 42, 641–647. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Popov, E.P. A model of nonlinearly hardening material for complex loading. Acta Mech. 1975, 21, 173–192. [Google Scholar] [CrossRef]
- Chaboche, J.L.; Dang Van, K.; Cordier, G.; Boley, B.A. Modelization of the Strain Memory Effect on the Cyclic Hardening of 316 Stainless Steel; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Ohno, N. A constitutive model of cyclic plasticity with a non-hardening strain region. J. Appl. Mech. 1982, 49, 721–727. [Google Scholar] [CrossRef]
- Chaboche, J.L. On some modifications of kinematic hardening to improve the description of ratcheting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Kourousis, K.I.; Saridis, G.J. Multiplicative AF kinematic hardening in plasticity. Int. J. Solids Struct. 2008, 45, 2861–2880. [Google Scholar] [CrossRef]
- Minnick, H.M. Gas Metal Arc Welding Handbook Textbook, 1st ed.; Goodheart–Willcox: Tinley Park, IL, USA, 2007. [Google Scholar]
- Murray, P.E. Selecting parameters for GMAW using dimensional analysis. Weld. J. 2002, 81, 125–131. [Google Scholar]
- Ozcelik, S.; Moore, K. Modeling, Sensing and Control of Gas Metal Arc Welding, 1st ed.; Elsevier Science Ltd.: Oxford, UK, 2003. [Google Scholar]
- Grong, O. Metallurgical Modelling of Welding. Institute of Materials, 1st ed.; Carlton House Terrace: London, UK, 1997. [Google Scholar]
- Liang, G.; Yuan, S. Study on the temperature measurement of AZ31B magnesium alloy in gas tungsten arc welding. Mater. Lett. 2008, 62, 2282–2284. [Google Scholar] [CrossRef]
- Bzymek, A.; Czuprýnski, A.; Fidali, M.; Jamrozik, W.; Timofiejczuk, A. Analysis of images recorded during welding processes. In Proceedings of the 9th International Conference on Quantitative InfraRed Thermography, Krakow, Poland, 2–5 July 2018. [Google Scholar]
- Tonković, Z.; Perić, M.; Surjak, M.; Garašić, I.; Boras, I.; Rodić, A.; Švaić, S. Numerical and experimental modeling of a T-joint fillet welding process. In Proceedings of the 11th International Conference on Quantitative InfraRed Thermography, Naples, Italy, 11–14 June 2012. [Google Scholar]
- Olabi, A.G.; Lostado, R.; Benyounis, K.Y. Review of Microstructures, Mechanical Properties, and Residual Stresses of Ferritic and Martensitic Stainless-Steel Welded. In Comprehensive Materials Processing; Welding and Bonding Technologies, Elsevier: Oxford, UK, 2014. [Google Scholar]
- ASTM E837-13a, Standard Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gage Method. Available online: https://www.astm.org/Standards/E837.htm (accessed on 20 December 2016).
- Vishay Precision Group. Measurement of Residual Stresses by the Hole-Drilling Strain Gage Method. Technical Note TN-503. 2010. Available online: http://www.vishaypg.com/docs/11053/tn503.pdf (accessed on 20 December 2016).
- ASTM E407-07 Standard Practice for Microetching Metals and Alloys. Available online: https://zh.scribd.com/document/259609551/ASTM-E407–07-StandardPractice-for-Microetching-Metals-and-Alloys (accessed on 20 December 2016).
- Schajer, G.S. Application of finite element calculations to residual stress measurements. ASME J. Eng. Mater. Technol. 1981, 103, 157–163. [Google Scholar] [CrossRef]
- ASTM E92-16, Standard Test Methods for Vickers Hardness and Knoop Hardness of Metallic Materials. Available online: http://www.astm.org/Standards/E92 (accessed on 20 December 2016).
- Barsoum, Z. Residual stress prediction and relaxation in welded tubular joint. Weld. World 2007, 51, 23–30. [Google Scholar] [CrossRef]
- Friedman, E. Thermomechanical analysis of the welding process using the finite element method. J. Press. Vessel-Technol. ASME 1975, 97, 206–213. [Google Scholar] [CrossRef]
- Muraki, T.; Bryan, J.; Masubuchi, K. Analysis of thermal stresses and metal movement during welding. J. Eng. Mater.-Technol. ASME 1975, 96, 81–84. [Google Scholar] [CrossRef]
- Karlsson, C.T. Finite element analysis of temperatures and stresses in a single-pass butt-welded pipe—Influence of mesh density and material modelling. Eng. Comput. 1989, 6, 133–141. [Google Scholar] [CrossRef]
- Karlsson, R.I.; Josefson, B.L. Three-dimensional finite element analysis of temperatures and stresses in a single-pass butt-welded pipe. J. Press. Vessel-Technol. ASME 1990, 112, 76–84. [Google Scholar] [CrossRef]
- Pardo, E.; Weckman, D.C. Prediction of weld pool and reinforcement dimensions of GMA welds using a finite-element model. Metall. Trans. B 1989, 20, 937–947. [Google Scholar] [CrossRef]
- Aarbogh, H.M.; Hamide, M.; Fjaer, H.G.; Mo, A.; Bellet, M. Experimental validation of finite element codes for welding deformations. J. Mater. Process. Technol. 2010, 210, 1681–1689. [Google Scholar] [CrossRef]
- Goldak, J.; Chakravarti, A.; Bibby, M. A new finite element model for welding heat sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Attarha, M.J.; Sattari-Far, I. Study on welding temperature distribution in thin welded plates through experimental measurements and finite element simulation. J. Mater. Process. Technol. 2011, 211, 688–694. [Google Scholar] [CrossRef]
- Bachorski, A.; Painter, M.J.; Smailes, A.J.; Wahab, M.A. Finite-element prediction of distortion during gas metal arc welding using the shrinkage volume approach. J. Mater. Process. Technol. 1999, 92, 405–409. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, G.; Cai, C.; Gao, H.; Wu, L. Fundamental studies on in process controlling angular distortion in asymmetrical double-sided double arc welding. J. Mater. Process. Technol. 2008, 205, 214–223. [Google Scholar] [CrossRef]
- Josefson, B.L. Prediction of residual stresses and distortions in welded structures. J. Offshore Mech. Arct. 1993, 115, 52–57. [Google Scholar] [CrossRef]
- Murthy, Y.V.; Rao, G.V.; Iyer, P.K. Numerical simulation of welding and quenching processes using transient thermal and thermo-elastic-plastic formulations. Comput. Struct. 1996, 60, 131–154. [Google Scholar] [CrossRef]
- Brickstad, B.; Josefson, B.L. A parametric study of residual stresses in multi-pass butt-welded stainless steel pipes. Int. J. Press. Vessels Pip. 1998, 75, 11–25. [Google Scholar] [CrossRef]
- Wen, S.W.; Farrugia, D.C. Finite element modelling of residual stress in pipe welds. Strain 2001, 37, 15–18. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H. Numerical simulation of temperature field and residual stress in multi-pass welds in stainless steel pipe and comparison with experimental measurements. Comput. Mater. Sci. 2006, 37, 269–277. [Google Scholar] [CrossRef]
- Armentani, E.; Esposito, R.; Sepe, R. The influence of thermal properties and preheating on residual stresses in welding. Int. J. Comput. Mater. Sci. Surf. Eng. 2007, 1, 146–162. [Google Scholar] [CrossRef]
- Sepe, R.; Armentani, E.; Lamanna, G.; Caputo, F. Evaluation by FEM of the influence of the preheating and postheating treatments on residual stresses in welding. Key Eng. Mater. 2015, 627, 93–96. [Google Scholar] [CrossRef]
- MARC User Guide, Version 2010; MSC Software Corporation: Santa Ana, CA, USA, 2010.
- Bag, S.; De, A. Development of a three-dimensional heat transfer model for the gas tungsten arc welding process using the finite element method coupled with a genetic algorithm based identification of uncertain input parameters. Metall. Mater. Trans. A 2008, 39, 2698–2710. [Google Scholar] [CrossRef]
- Lee, J.; Um, K. A comparison in a back-bead pre-diction of gas metal arc welding using multiple regression analysis and artificial neural network. Opt. Laser Eng. 2000, 4, 149–158. [Google Scholar] [CrossRef]
- Lindgren, L.E. Computational Welding Mechanics: Thermomechanical and Microstructural Simulations, 1st ed.; Woodhead Publishing: Cambridge, UK, 2007. [Google Scholar]
- Friedman, E. Numerical simulation of the gas tungsten-arc welding process. In Proceedings of the Numerical Modeling of Manufacturing Processes, ASME Winter Annual Meeting, Atlanta, GA, USA, 27 November–2 December 1977. [Google Scholar]
- Hibbitt, H.D.; Marcal, P.V. A numerical, thermo-mechanical model for the welding and subsequent loading of a fabricated structure. Comput. Struct. 1973, 3, 1145–1174. [Google Scholar] [CrossRef]
- Benzley, S.E.; Perry, E.; Merkley, K.; Clark, B.; Sjaardama, G. A comparison of all hexagonal and all tetrahedral finite element meshes for elastic and elasto-plastic analysis. In Proceedings of the 4th International Meshing Roundtable, Sandia National Laboratories, Albuquerque, NM, USA, 16–17 October 1995. [Google Scholar]
- Cifuentes, A.O.; Kalbag, A. A performance study of tetrahedral and hexahedral elements in 3-D finite element structural analysis. Finite Elem. Anal. Des. 1992, 12, 313–318. [Google Scholar] [CrossRef]
- Da Nóbrega, J.A.; Diniz, D.D.; Silva, A.A.; Maciel, T.M.; de Albuquerque, V.H.C.; Tavares, J.M.R. Numerical evaluation of temperature field and residual stresses in an API 5L X80 steel welded joint using the finite element method. Metals 2016, 6, 28. [Google Scholar] [CrossRef]
- Apostol, G.; Solomon, G.; Iordchescu, D. Input parameters influence on the residual stress and distortions at laser welding using finite element analysis. Ser. D Mech. Eng. 2012, 74, 153–164. [Google Scholar]









| Inputs | Specimen 01 | Specimen 02 | Specimen 03 |
|---|---|---|---|
| Current (amps) | 140.0 | 210.0 | 260.0 |
| Voltage (volts) | 26.0 | 28.0 | 35.0 |
| Speed (mm/s) | 6.0 | 6.0 | 6.0 |
| Heat Flux (KJ/mm) | 0.424 | 0.686 | 1.061 |
| Weld bead dimensions | |||
| Height (mm) | 1.3 | 1.5 | 2.5 |
| Width (mm) | 9.5 | 8.7 | 12.0 |
| Specimen | Melting Point (°C) | Contact_P_Init (N/s/K) | Contact_P_Center (N/s/K) | Contact_P_End (N/s/K) | Contact_P1_P2 (N/s/K) | Contact_P_G (N/s/K) | Face_Film (N/s/K/mm) |
| 01 | 1427 | 17 | 10 | 19 | 193 | 66 | 0.00052 |
| 02 | 1425 | 257 | 65 | 189 | 195 | 176 | 0.00071 |
| 03 | 1429 | 203 | 662 | 247 | 159 | 182 | 0.00093 |
| Specimen | Face_Film 2 (N/s/K/mm) | Face_Film 3 (N/s/K/mm) | Forward Length (mm) | Rear Length (mm) | Width (mm) | Depth (mm) | |
| 01 | 0.00039 | 0.00041 | 1.0 | 7.8 | 24.9 | 4.3 | 1.988 |
| 02 | 0.00039 | 0.00033 | 1.8 | 7.4 | 23.8 | 4.3 | 3.028 |
| 03 | 0.0008 | 0.00068 | 1.6 | 5.2 | 23.1 | 5.4 | 6.349 |
| Specimen | FEM (°) | Experimental (°) | Error (%) |
|---|---|---|---|
| 1 | 4.98 | 4.64 | 7.3 |
| 2 | 5.12 | 4.723 | 8.4 |
| 3 | 5.31 | 4.934 | 7.6 |
| Sp. | Res. Str. (MPa) | Rosette 1 | Rosette 2 | Rosette 3 | Rosette 4 | Rosette 5 | Rosette 6 |
|---|---|---|---|---|---|---|---|
| 1 | σx | 481.9 | 477.2 | 513.1 | 514.9 | 477.4 | 477.5 |
| σy | 200.0 | 201.6 | 219.0 | 222.1 | 201.5 | 203.8 | |
| 2 | σx | 517.0 | 512.1 | 541.0 | 540.7 | 506.2 | 503.5 |
| σy | 221.8 | 223.5 | 246.5 | 238.8 | 230.6 | 224.5 | |
| 3 | σx | 575.9 | 567.9 | 600.9 | 596.8 | 582.5 | 581.2 |
| σy | 259.9 | 249.5 | 294.4 | 293.5 | 264.0 | 255.1 |
| Depth (mm) | Rosette 1 | Rosette 2 | Rosette 3 |
| ε1/ε2/ε3/α | ε1/ε2/ε3/α | ε1/ε2/ε3/α | |
| 0.127 | −31/−7/−18/−34.8 | −30/−7/−19/−36.3 | −33/−8/−20/−35.3 |
| 0.254 | −40/−11/−24/−34.5 | −39/−11/−25/−35.8 | −41/−11/−25/−35.0 |
| 0.508 | −43/−14/−27/−34.5 | −42/−14/−28/−35.8 | −43/−14/−28/−35.4 |
| 0.762 | −46/−17/−30/−34.5 | −45/−18/−31/−35.4 | −47/−18/−31/−34.6 |
| 1.016 | −48/−18/−32/−35.0 | −48/−18/−32/−35.0 | −49/−18/−32/−34.6 |
| 1.27 | −50/−19/−33/−34.6 | −50/−19/−34/−35.4 | −52/−19/−34−34.7 |
| Depth (mm) | Rosette 4 | Rosette 5 | Rosette 6 |
| ε1/ε2/ε3/α | ε1/ε2/ε3/α | ε1/ε2/ε3/α | |
| 0.127 | −32/−8/−21/−36.7 | −30/−7/−19/−36.3 | −29/−7/−20/−37.7 |
| 0.254 | −40/−11/−26/−36.2 | −37/−10/−26/−37.8 | −38/−10/−25/−26.6 |
| 0.508 | −42/−14/−29/−36.6 | −40/−13/−29/−37.8 | −41/−14/−29/−37.0 |
| 0.762 | −46/−19/−32/−35.4 | −43/−17/−32/−37.4 | −43/−16/−31/−37.0 |
| 1.016 | −49/−20/−32/−33.7 | −46/−17/−33/−37.0 | −46/−17/−33/−36.9 |
| 1.27 | −52/−21/−34/−33.9 | −50/−18/−34/−35.8 | −50/−18/−34/−35.8 |
| Depth (mm) | Rosette 1 | Rosette 2 | Rosette 3 |
| ε1/ε2/ε3/α | ε1/ε2/ε3/α | ε1/ε2/ε3/α | |
| 0.127 | −33/−8/−20/−35.3 | −32/−8/−21/−36.7 | −35/−10/−22/−35.3 |
| 0.254 | −42/−13/−27/−35.3 | −41/−13/−27/−35.8 | −43/−11/−27−35.8 |
| 0.508 | −44/−15/−29/−35.4 | −43/−14/−28/−35.4 | −45/−14/−31−36.8 |
| 0.762 | −47/−17/−31/−35.0 | −46/−16/−30/−35.0 | −47/−16/−32/−36.2 |
| 1.016 | −48/−19/−33/−35.4 | −48/−18/−33/−35.8 | −50/−18/−35/−36.5 |
| 1.27 | −50/−20/−34/−35.0 | −50/−20/−34/−35.0 | −51/−19/−36/−36.5 |
| Depth (mm) | Rosette 4 | Rosette 5 | Rosette 6 |
| ε1/ε2/ε3/α | ε1/ε2/ε3/α | ε1/ε2/ε3/α | |
| 0.127 | −34/−9/−22/−36.2 | −32/−9/−21/−36.3 | −32/−8/−21/−36.7 |
| 0.254 | −43/−12/−28/−36.2 | −42/−13/−28/−36.1 | −41/−13/−28/−36.6 |
| 0.508 | −46/−15/−31/−36.2 | −44/−15/−29/−35.4 | −43/−14/−29/−36.2 |
| 0.762 | −49/−19/−33/−35.0 | −45/−17/−30/−34.9 | −45/−16/−31/−36.2 |
| 1.016 | −50/−20/−34/−35.0 | −47/−19/−31/−34.1 | −47/−18/−33−36.2 |
| 1.27 | −52/−19/−34/−34.7 | −50/−21/−33/−33.7 | −50/−19/−34−35.4 |
| Depth (mm) | Rosette 1 | Rosette 2 | Rosette 3 |
| ε1/ε2/ε3/α | ε1/ε2/ε3/α | ε1/ε2/ε3/α | |
| 0.127 | −36/−10/−24/−36.6 | −35/−9/−24/−37.4 | −39/−13/−26/−35.7 |
| 0.254 | −46/−16/−32/−36.5 | −44/−15/−31/−36.9 | −51/−17/−35/−36.4 |
| 0.508 | −48/−19/−34/−36.1 | −47/−17/−33/−36.5 | −54/−21/−39/−36.8 |
| 0.762 | −52/−21/−38/−36.8 | −51/−20/−36/−36.1 | −61/−24/−43/−36.0 |
| 1.016 | −57/−24/−42/−36.8 | −55/−24/−43/−38.2 | −63/−26/−44/−35.4 |
| 1.27 | −61/−27/−45/−36.4 | −60/−25/−44/−36.7 | −61/−27/−46/−37.1 |
| Depth (mm) | Rosette 4 | Rosette 5 | Rosette 6 |
| ε1/ε2/ε3/α | ε1/ε2/ε3/α | ε1/ε2/ε3/α | |
| 0.127 | −38/−13/−26/−36.2 | −36/−10/−25/−37.4 | −35/−9/−25/−38.3 |
| 0.254 | −50/−18/−35/−36.4 | −44/−16/−33/−38.1 | −45/−15/−33/−37.9 |
| 0.508 | −55/−22/−39/−36.1 | −46/−19/−34/−37.0 | −47/−18/−34/−36.9 |
| 0.762 | −62/−25/−43/−35.4 | −50/−21/−37/−36.9 | −51/−20/−37/−36.8 |
| 1.016 | −64/−27/−45/−35.4 | −56/−22/−42/−37.7 | −56/−23/−41/−36.8 |
| 1.27 | −62/−28/−47/−37.1 | −61/−25/−43/−35.7 | −60/−26/−44/−36.4 |
| Principal Stresses | Depth (mm) | Rosette 1 | Rosette 2 | Rosette 3 | Rosette 4 | Rosette 5 | Rosette 6 |
|---|---|---|---|---|---|---|---|
| FEM/Exp. | FEM/Exp. | FEM/Exp. | FEM/Exp. | FEM/Exp. | FEM/Exp. | ||
| σI (MPa) | 0.127 | 467.9/461.9 | 465.6/460.4 | 501.6/496.3 | 499.4/494.1 | 465.5/460.4 | 463.6/458.4 |
| 0.254 | 226.4/252.1 | 225.0/250.4 | 234.4/260.0 | 233.5/259.0 | 222.9/247.7 | 223.4/248.5 | |
| 0.508 | 144.1/128.8 | 143.3/135.5 | 146.3/137.9 | 145.5/137.4 | 141.4/134.1 | 142.2/135.1 | |
| 0.762 | 108.4/92.7 | 108.1/83.0 | 110.1/85.8 | 109.1/84.6 | 106.9/82.2 | 107.4/81.9 | |
| 1.016 | 79.7/76.8 | 79.7/75.6 | 81.6/76.8 | 80.4/75.4 | 79.4/74.9 | 79.5/74.9 | |
| 1.27 | 52.9/68.3 | 53.4/70.3 | 55.3/72.4 | 53.9/71.2 | 53.9/70.9 | 53.6/70.9 | |
| MAE | 13.86 | 14.09 | 14.23 | 14.27 | 11.93 | 14.13 | |
| σII (MPa) | 0.127 | 194.7/197.0 | 196.9/199.1 | 214.5/217.0 | 216.5/219.2 | 196.7/199.1 | 198.4/201.0 |
| 0.254 | 120.7/114.2 | 122.0/115.2 | 126.1/117.1 | 127.7/118.0 | 120.0/112.2 | 120.3/111.4 | |
| 0.508 | 68.6/66.2 | 69.3/72.4 | 69.1/73.0 | 70.1/73.4 | 67.4/70.8 | 67.3/72.8 | |
| 0.762 | 47.9/49.8 | 48.4/43.8 | 47.6/44.3 | 48.3/45.5 | 46.9/42.9 | 46.7/41.5 | |
| 1.016 | 36.8/42.2 | 37.2/40.8 | 36.3/41.1 | 36.9/42.4 | 35.9/40.1 | 35.8/40.1 | |
| 1.27 | 29.9/38.6 | 30.2/39.1 | 29.3/39.6 | 29.8/40.8 | 29.1/38.5 | 29.0/38.5 | |
| MAE | 5.00 | 4.87 | 5.63 | 5.85 | 4.44 | 6.01 |
| Principal Stresses | Depth (mm) | Rosette 1 | Rosette 2 | Rosette 3 | Rosette 4 | Rosette 5 | Rosette 6 |
|---|---|---|---|---|---|---|---|
| FEM/Exp. | FEM/Exp. | FEM/Exp. | FEM/Exp. | FEM/Exp. | FEM/Exp. | ||
| σI (MPa) | 0.127 | 501.9/496.3 | 499.6/494.1 | 528.8/523.3 | 524.4/518.8 | 493.6/487.3 | 488.8/494.1 |
| 0.254 | 239.5/266.6 | 235.5/261.8 | 250.1/277.2 | 250.9/278.1 | 253.4/270.4 | 281.4/265.7 | |
| 0.508 | 150.3/140.9 | 147.1/137.9 | 156.3/148.5 | 157.5/149.5 | 151.2/140.8 | 130.5/139.8 | |
| 0.762 | 111.8/86.8 | 109.9/85.0 | 116.5/88.7 | 116.9/90.0 | 111.2/82.7 | 56.2/84.7 | |
| 1.016 | 80.7/75.9 | 80.3/76.6 | 84.7/80.9 | 84.1/78.6 | 78.5/72.8 | 69.6/75.4 | |
| 1.27 | 51.9/69.7 | 52.9/69.7 | 55.1/73.0 | 53.5/72.5 | 47.9/68.2 | 90.7/70.3 | |
| MAE | 14.97 | 14.39 | 15.00 | 15.35 | 14.71 | 14.17 | |
| σII (MPa) | 0.127 | 216.0/217.0 | 218.3/219.2 | 241.4/243.9 | 232.7/234.9 | 225.1/226.0 | 218.6/219.2 |
| 0.254 | 130.9/127.6 | 129.5/126.7 | 127.1/122.7 | 135.9/127.5 | 132.7/129.5 | 130.4/128.5 | |
| 0.508 | 73.2/76.0 | 71.4/73.0 | 72.2/77.3 | 74.2/79.2 | 72.84/76.0 | 72.2/74.0 | |
| 0.762 | 50.8/43.7 | 49.3/41.8 | 45.1/43.1 | 51.0/46.8 | 50.2/42.4 | 49.9/42.1 | |
| 1.016 | 38.9/42.0 | 37.6/41.3 | 36.3/42.8 | 38.8/43.8 | 38.2/40.7 | 38.1/41.1 | |
| 1.27 | 31.5/39.7 | 30.4/39.7 | 29.2/40.3 | 31.4/39.6 | 30.9/39.8 | 30.9/39.1 | |
| MAE | 4.30 | 4.31 | 5.27 | 5.50 | 4.40 | 3.90 |
| Principal Stresses | Depth (mm) | Rosette 1 | Rosette 2 | Rosette 3 | Rosette 4 | Rosette 5 | Rosette 6 |
|---|---|---|---|---|---|---|---|
| FEM/Exp. | FEM/Exp. | FEM/Exp. | FEM/Exp. | FEM/Exp. | FEM/Exp. | ||
| σI (MPa) | 0.127 | 559.1/552.5 | 554.0/548.2 | 587.4/583.8 | 578.9/572.6 | 568.0/561.7 | 564.3/557.5 |
| 0.254 | 278.68/296.2 | 257.6/285.8 | 301.0/328.7 | 302.3/321.0 | 272.5/290.7 | 291.5/298.3 | |
| 0.508 | 166.9/154.7 | 161.7/153.1 | 188.3/176.0 | 188.7/177.0 | 161.4/149.9 | 166.6/153.7 | |
| 0.762 | 127.1/98.2 | 123.7/95.4 | 136.5/113.9 | 142.7/114.5 | 123.4/94.2 | 126.2/96.5 | |
| 1.016 | 95.8/91.9 | 94.3/90.5 | 103.7/99.5 | 104.9/101.0 | 94.2/92.1 | 94.3/90.4 | |
| 1.27 | 66.9/86.5 | 67.3/85.8 | 67.0/87.3 | 69.5/88.6 | 67.7/85.9 | 65.0/85.1 | |
| MAE | 15.80 | 15.54 | 15.10 | 14.66 | 14.26 | 13.38 | |
| σII (MPa) | 0.127 | 253.1/255.1 | 243.7/245.9 | 288.3/291.0 | 286.1/288.8 | 257.7/259.3 | 248.4/250.0 |
| 0.254 | 155.1/149.5 | 148.9/142.8 | 169.6/162.6 | 166.3/164.6 | 153.6/149.29 | 150.5/147.3 | |
| 0.508 | 86.1/88.9 | 83.8/84.6 | 95.2/100.3 | 97.3/102.2 | 85.8/87.74 | 85.6/86.9 | |
| 0.762 | 60.8/52.0 | 58.3/49.8 | 62.4/59.6 | 67.6/60.7 | 56.4/50.97 | 56.9/50.3 | |
| 1.016 | 45.9/52.3 | 44.7/52.3 | 50.3/56.3 | 51.8/57.7 | 45.4/50.64 | 45.6/50.8 | |
| 1.27 | 37.8/51.7 | 36.2/49.7 | 49.3/52.0 | 41.97/53.3 | 36.7/49.55 | 37.0/50.3 | |
| MAE | 6.56 | 6.44 | 4.36 | 5.60 | 5.22 | 5.20 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lostado Lorza, R.; Corral Bobadilla, M.; Martínez Calvo, M.Á.; Villanueva Roldán, P.M. Residual Stresses with Time-Independent Cyclic Plasticity in Finite Element Analysis of Welded Joints. Metals 2017, 7, 136. https://doi.org/10.3390/met7040136
Lostado Lorza R, Corral Bobadilla M, Martínez Calvo MÁ, Villanueva Roldán PM. Residual Stresses with Time-Independent Cyclic Plasticity in Finite Element Analysis of Welded Joints. Metals. 2017; 7(4):136. https://doi.org/10.3390/met7040136
Chicago/Turabian StyleLostado Lorza, Ruben, Marina Corral Bobadilla, María Ángeles Martínez Calvo, and Pedro María Villanueva Roldán. 2017. "Residual Stresses with Time-Independent Cyclic Plasticity in Finite Element Analysis of Welded Joints" Metals 7, no. 4: 136. https://doi.org/10.3390/met7040136
APA StyleLostado Lorza, R., Corral Bobadilla, M., Martínez Calvo, M. Á., & Villanueva Roldán, P. M. (2017). Residual Stresses with Time-Independent Cyclic Plasticity in Finite Element Analysis of Welded Joints. Metals, 7(4), 136. https://doi.org/10.3390/met7040136