FEM Simulation of Dissimilar Aluminum Titanium Fiber Laser Welding Using 2D and 3D Gaussian Heat Sources
Abstract
:1. Introduction
2. Experimental Setup
3. Numerical Model
3.1. Model for the Plates
3.2. 2D Heat Source
3.3. 3D Heat Source
4. Results and Discussion
4.1. Metallurgical Characterization of Weld
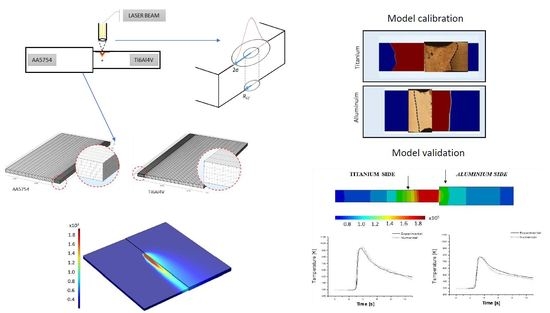
4.2. Calibration of the Model
4.3. Validation of the Model
5. Conclusions
- (1)
- The calculations for the fusion zone dimensions were accurate both for the 2D and the 3D heat source. By using that 2D heat source, a better matching of numeric and experimental results was obtained at the three levels at which the molten zone sizes were taken.
- (2)
- In the longitudinal section, the numerical results were not as accurate for both of the heat sources. For the 2D one, a teardrop shape of the molten weld pool formed while the 3D heat source produced an elliptical one. It is possible to conclude that the 3D heat source can better approximate the heat flux during laser welding and the maximum temperature gradients, which determined the change in the grain growth direction in the titanium side.
- (3)
- The overall thermal cycle accuracy was good for 2D and 3D heat sources. However, the 3D heat source provided better results for the cooling rate simulation.
Author Contributions
Conflicts of Interest
References
- Oliveira, J.P.; Zeng, Z.; Andrei, C.; Braz Fernandes, F.M.; Miranda, R.M.; Ramirez, A.J.; Omori, T.; Zhou, N. Dissimilar laser welding of superelastic NiTi and CuAlMn shape memory alloys. Mater. Des. 2017, 128, 166–175. [Google Scholar] [CrossRef]
- Casalino, G.; Guglielmi, P.; Lorusso, V.D.; Mortello, M.; Peyre, P.; Sorgente, D. Laser offset welding of AZ31B magnesium alloy to 316 stainless steel. J. Mater. Process. Technol. 2017, 242, 49–59. [Google Scholar] [CrossRef]
- Zeng, X.; Oliveira, J.P.; Yang, M.; Song, D.; Peng, B. Functional fatigue behavior of NiTi-Cu dissimilar laser welds. Mater. Des. 2017, 114, 282–287. [Google Scholar] [CrossRef]
- Katayama, S. Handbook of Laser Welding Technologies; Woodhead Publishing Limited: Sawston, UK, 2013. [Google Scholar]
- Casalino, G.; Mortello, M.; Peyre, P. Yb–YAG laser offset welding of AA5754 and T40 butt joint. J. Mater. Process. Technol. 2015, 223, 139–149. [Google Scholar] [CrossRef]
- Rosenthal, D. Mathematical theory of heat distribution during welding and cutting. Weld. J. 1941, 20, 220–234. [Google Scholar]
- Zeng, Z.; Li, X.; Miao, Y.; Wu, G.; Zhao, Z. Numerical and experiment analysis of residual stress on magnesium alloy and steel butt joint by hybrid laser-TIG welding. Comput. Mater. Sci. 2011, 50, 1763–1769. [Google Scholar] [CrossRef]
- Pham, S.M.; Tran, V.P. Study on the Structure Deformation in the Process of Gas Metal Arc Welding (GMAW). Am. J. Mech. Eng. 2014, 2, 120–124. [Google Scholar]
- Dhinakaran, V.; Suraj Khope, N.S.S.; Sankaranarayanasamy, K. Numerical Prediction of Weld Bead Geometry in Plasma Arc Welding of Titanium Sheets Using COMSOL. In Proceedings of the 2014 COMSOL Conference in Bangalore, Bangalore, India, 13–14 October 2014. [Google Scholar]
- Casalino, G.; Hu, S.J.; Hou, W. Deformation prediction and quality evaluation of the gas metal arc welding butt weld. Proc. Inst. Mech. Eng. Part B 2003, 217, 1615–1622. [Google Scholar] [CrossRef]
- Zeng, Z.; Wang, L.; Wang, Y.; Zhang, H. Numerical and experimental investigation on temperature distribution of the discontinuous welding. Comput. Mater. Sci. 2009, 44, 1153–1162. [Google Scholar] [CrossRef]
- Casalino, G.; Michelangelo, M. A FEM model to study the fiber laser welding of Ti6Al4V thin sheets. Int. J. Adv. Manuf. Technol. 2016, 86, 1339–1346. [Google Scholar] [CrossRef]
- Azizpour, M.; Ghoreishi, M.; Khorram, A. Numerical simulation of laser beam welding of Ti6Al4V sheet. J. Comput. Appl. Res. Mech. Eng. 2015, 4, 145–154. [Google Scholar]
- Falk, N.; Flaviu, S.; Benjamin, K.; Jean, P.B.; Jorg, H. Optimization strategies for laser welding high alloy steel sheets. Phys. Proced. 2014, 56, 1242–1251. [Google Scholar]
- Comsol Multiphysics, version 5.2a; Software for Multiphysics Modeling; COMSOL: Stockholm, Sweden, 2016.
- Contuzzi, N.; Campanelli, S.L.; Casalino, G.; Ludovico, A.D. On the role of the Thermal Contact Conductance during the Friction Stir Welding of an AA5754-H111 butt joint. Appl. Therm. Eng. 2016, 104, 263–273. [Google Scholar] [CrossRef]
- Casalino, G.; Mortello, M.; Peyre, P. FEM Analysis of Fiber Laser Welding of Titanium and Aluminum. Procedia CIRP 2016, 41, 992–997. [Google Scholar] [CrossRef]
- Teixeira, P.R.D.F.; Araújo, D.B.D.; Cunda, L.A.B.D. Study of the gaussian distribution heat source model applied to numerical thermal simulations of tig welding processes. Ciênc. Eng. 2014, 23, 115–122. [Google Scholar] [CrossRef]
- Steen, W.M.; Mazumder, J. Laser Material Processing; Springer: Berlin, Germany, 2010. [Google Scholar]
- Goldak, J.; Akhlagi, M. Computational Welding Mechanics; Springer: Ottawa, ON, Canada, 2005; pp. 26–27. [Google Scholar]
- Lv, S.X.; Jing, X.J.; Huang, Y.X.; Xu, Y.Q.; Zheng, C.Q.; Yang, S.Q. Investigation on TIG arc welding–brazing of Ti/Al dissimilar alloys with Al based fillers. Sci. Technol. Weld. Join. 2012, 17, 519–524. [Google Scholar] [CrossRef]
- Lutjering, G.; Williams, J.C. Titanium (Engineering Materials and Processes), 2nd ed.; Springer: Berlin, Germany; New York, NY, USA, 2007. [Google Scholar]
- Akman, E.; Demir, A.; Canel, T.; Sınmazcelik, T. Laser welding of Ti6Al4V titanium alloys. J. Mater. Process. Technol. 2009, 209, 3705–3713. [Google Scholar] [CrossRef]
- Xu, P.; Li, L.; Zhang, C. Microstructure characterization of laser welded Ti-6Al-4V fusion zones. Mater. Charact. 2014, 87, 179–185. [Google Scholar] [CrossRef]
- Kumar, S.; Nadendla, H.B.; Scamans, G.M.; Eskin, D.G.; Fan, Z. Solidification behavior of an AA5754 alloy ingot cast with high impurity content. Int. J. Mater. Res. 2012, 103, E1–E7. [Google Scholar] [CrossRef]
- Raghavan, V. Phase Diagram Evaluations: Section II. J. Ph. Equilib. Diffus. 2005, 26, 171–172. [Google Scholar] [CrossRef]
- ASM Specialty Handbook: Aluminum and Aluminum Alloys; Davis, J.R. (Ed.) ASM International: Novelty, OH, USA, 1993. [Google Scholar]
- Porter, D.A.; Easterling, K.E. Phase Transformations in Metals and Alloys; Chapman & Hall: London, UK, 1992. [Google Scholar]
- Verhoeven, J.D. Fundamentals of Physical Metallurgy; Wiley: Hoboken, NJ, USA, 1975. [Google Scholar]
- Leo, P.; D’Ostuni, S.; Casalino, G. Hybrid welding of AA5754 annealed alloy: Role of post weld heat treatment on microstructure and mechanical properties. Mater. Des. 2016, 90, 777–786. [Google Scholar] [CrossRef]
- Bailey, N. Welding Dissimilar Metals; The Welding Institute: Cambridge, UK, 1986. [Google Scholar]
- Gao, M.; Chen, C.; Gu, Y.; Zeng, X. Microstructure and tensile behavior of laser arc hybrid welded dissimilar Al and Ti alloys. Materials 2014, 7, 1590–1602. [Google Scholar] [CrossRef]
- Sorensen, M.B. Simulation of Welding Distortion in Ship Section. Ph.D. Thesis, University of Denmark, Lyngby, Denmark, 1999. [Google Scholar]
- Messler, R.W. Principles of Welding; Wiley-VCH, John Wiley & Sons, Inc.: Singapore, 2004. [Google Scholar]
















| AA5754 | ||||||||
| Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti | Al |
| 0.40 | 0.40 | 0.10 | 0.50 | 2.6–3.6 | 0.30 | 0.20 | <0.15 | balance |
| Ti6Al4V | ||||||||
| C | Fe | N2 | O2 | Al | V | H2 | Ti | C |
| <0.08 | <0.25 | <0.05 | <0.2 | 5.5 | 3.5 | <0.0375 | balance | <0.08 |
| Property | AA5754 | Ti6Al4V |
|---|---|---|
| Young modulus [GPa] | 70 | 114 |
| Poisson ratio | 0.3 | 0.3 |
| Density [g/cm3] | 2.7 | 4.4 |
| Liquidus Temperature [K] | 870 | 1923 |
| Solidus Temperature [K] | 856 | 1880 |
| AA5754 | |
|---|---|
| Temperature | Thermal Conductivity [W/mK] |
| 293 | 138 |
| 373 | 147.2 |
| 473 | 152.7 |
| 573 | 162.7 |
| 673 | 152.7 |
| 773 | 158.75 |
| 873 | 138 |
| 1773 | 138 |
| Ti6Al4V | |
|---|---|
| Temperature | Thermal Conductivity [W/mK] |
| 293 | 6.01 |
| 773.15 | 14.78 |
| 793.15 | 15 |
| 823.15 | 15.15 |
| 953.15 | 17.20 |
| 993.15 | 17.80 |
| 1013.15 | 18.30 |
| 1053.15 | 18.80 |
| 1093.15 | 19.50 |
| 1113.15 | 20 |
| 1133.15 | 20.50 |
| 1153.15 | 21 |
| 1173.15 | 21.60 |
| 1273.15 | 23.91 |
| 1933.15 | 34.3 |
| Aluminum Fusion Zone | 2D Heat Source | 3D Heat Source | Experimental Data |
|---|---|---|---|
| Top | 118 | 136 | 116 |
| Middle | 120 | 135 | 112 |
| Bottom | 114 | 135 | 108 |
| Titanium Fusion Zone | 2D Heat Source | 3D Heat Source | Experimental Data |
|---|---|---|---|
| Top | 232 | 204 | 225 |
| Middle | 207 | 196 | 198 |
| Bottom | 226 | 187 | 196 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Ostuni, S.; Leo, P.; Casalino, G. FEM Simulation of Dissimilar Aluminum Titanium Fiber Laser Welding Using 2D and 3D Gaussian Heat Sources. Metals 2017, 7, 307. https://doi.org/10.3390/met7080307
D’Ostuni S, Leo P, Casalino G. FEM Simulation of Dissimilar Aluminum Titanium Fiber Laser Welding Using 2D and 3D Gaussian Heat Sources. Metals. 2017; 7(8):307. https://doi.org/10.3390/met7080307
Chicago/Turabian StyleD’Ostuni, Sonia, Paola Leo, and Giuseppe Casalino. 2017. "FEM Simulation of Dissimilar Aluminum Titanium Fiber Laser Welding Using 2D and 3D Gaussian Heat Sources" Metals 7, no. 8: 307. https://doi.org/10.3390/met7080307
APA StyleD’Ostuni, S., Leo, P., & Casalino, G. (2017). FEM Simulation of Dissimilar Aluminum Titanium Fiber Laser Welding Using 2D and 3D Gaussian Heat Sources. Metals, 7(8), 307. https://doi.org/10.3390/met7080307