Physically-Based Modeling and Characterization of Hot Flow Behavior in an Interphase-Precipitated Ti-Mo Microalloyed Steel
Abstract
:1. Introduction
2. Experimental Procedures
3. Results and Discussion
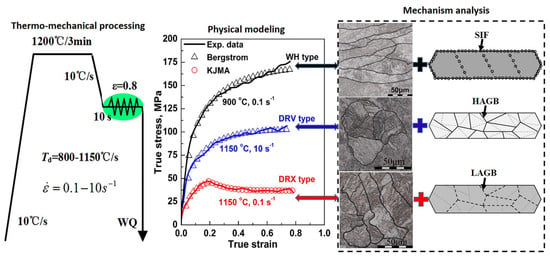
3.1. Hot Flow Behaviors
3.2. Peak Stress Analysis
3.3. Physically-Based Constitutive Analysis
3.4. Experimental Verification and Mechanism Analysis
4. Conclusions
- (1)
- The peak stress as a function of deformation temperature and strain rate was determined as:
- (2)
- Under conditions where DRV or WH was dominant, the hot flow behavior could be modeled using the Bergstrom equation; once DRX was initiated, the coupling of the Bergstrom and KJMA’s models was capable of predicting the flow behaviors in the whole hot deformation.
- (3)
- The values of U and ρp exhibited an approximately positive linear relationship with the lnZ parameter, while the Ω dropped with increasing Z value. Meanwhile, the nA value varied between 1.2 and 2.1 with lnZ, indicating the variation in the mechanisms of DRX with deformation conditions.
- (4)
- After the microstructure deformed at 900 °C and 0.1 s−1, the severely pancaked prior austenitic grains remained; with increasing deformation temperature above 950 °C and 0.1 s−1, the fully-equiaxed DRX grains formed through rearrangement or annihilation of dislocations. However, as the strain rate increased to 10 s−1 for different deformation temperatures, WH and DRV were dominant, resulting in some deformation bands and substructures in the large pancaked prior austenite grains.
- (5)
- With increasing the temperature from 900–1150 °C at 0.1 s−1, the fraction of LAGBs of 2–5° dropped by ~33.6%, with greatly increased high angle austenitic grain boundaries (~46.2%) due to a pronounced DRX phenomenon. With increasing strain rate to 10 s−1 at 1150 °C, the fraction of LAGBs of 2–5° increased to ~37.5%, which was associated with inhibition of DRX.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mukherjee, S.; Timokhina, I.B.; Zhu, C.; Ringer, S.P.; Hodgson, P.D. Three-dimensional atom probe microscopy study of interphase precipitation and nanoclusters in thermomechanically treated titanium–molybdenum steels. Acta Mater. 2013, 61, 2521–2530. [Google Scholar] [CrossRef]
- Cai, M.H.; Ding, H.; Lee, Y.K.; Tang, Z.Y.; Zhang, J.S. Effects of Si on Microstructural Evolution and Mechanical Properties of Hot-rolled Ferrite and Bainite Dual-phase Steels. ISIJ Int. 2011, 51, 476–481. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.J.; De Cooman, B.C. Effect of micro-alloying elements on the stretch-flangeability of dual phase steel. Mater. Sci. Eng. A 2012, 536, 231–238. [Google Scholar] [CrossRef]
- Kamikawa, N.; Abe, Y.; Miyamoto, G.; Funakawa, Y.; Furuhara, T. Tensile behavior of Ti,Mo-added low carbon steels with interphase precipitation. ISIJ Int. 2014, 54, 212–221. [Google Scholar] [CrossRef]
- Rahnama, A.; Clark, S.; Janik, V.; Sridhar, S. A phase-field model investigating the role of elastic strain energy during the growth of closely spaced neighbouring interphase precipitates. Comput. Mater. Sci. 2018, 142, 437–443. [Google Scholar] [CrossRef]
- Funakawa, Y.; Shiozaki, T.; Tomita, K.; Yamamoto, T.; Maeda, E. Development of high strength hot-rolled sheet steel consisting of ferrite and nanometer-sized carbides. ISIJ Int. 2004, 44, 1945–1951. [Google Scholar] [CrossRef]
- Yen, H.W.; Huang, C.Y.; Yang, J.R. Characterization of interphase-precipitated nanometer-sized carbides in a Ti–Mo-bearing steel. Scr. Mater. 2009, 61, 616–619. [Google Scholar] [CrossRef]
- Wang, J.; Hodgson, P.D.; Bikmukhametov, I.; Miller, M.K.; Timokhina, I. Effects of hot-deformation on grain boundary precipitation and segregation in Ti-Mo microalloyed steels. Mater. Des. 2018, 141, 48–56. [Google Scholar] [CrossRef]
- Kim, Y.W.; Kim, J.H.; Hong, S.G.; Lee, C.S. Effects of rolling temperature on the microstructure and mechanical properties of Ti–Mo microalloyed hot-rolled high strength steel. Mater. Sci. Eng. A 2014, 605, 244–252. [Google Scholar] [CrossRef]
- Yong, W.K.; Hong, S.G.; Huh, Y.H.; Chong, S.L. Role of rolling temperature in the precipitation hardening characteristics of Ti–Mo microalloyed hot-rolled high strength steel. Mater. Sci. Eng. A 2014, 615, 255–261. [Google Scholar] [CrossRef]
- Hamada, A.; Khosravifard, A.; Porter, D.; Pentti Karjalainen, L. Physically based modeling and characterization of hot deformation behavior of twinning-induced plasticity steels bearing vanadium and niobium. Mater. Sci. Eng. A 2017, 703, 85–96. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Cabrera, J.M.; Najafizadeh, A. Constitutive relationships for hot deformation of austenite. Acta Mater. 2011, 59, 6441–6448. [Google Scholar] [CrossRef]
- Feng, H.; Jiang, Z.H.; Li, H.B.; Jiao, W.C.; Li, X.X.; Zhu, H.C.; Zhang, S.C.; Zhang, B.B.; Cai, M.H. Hot deformation behavior and microstructural evolution of high nitrogen martensitic stainless steel 30Cr15Mo1N. Steel Res. Int. 2017, 88, 1700149. [Google Scholar] [CrossRef]
- Cram, D.G.; Fang, X.Y.; Zurob, H.S.; Bréchet, Y.J.M.; Hutchinson, C.R. The effect of solute on discontinuous dynamic recrystallization. Acta Mater. 2012, 60, 6390–6404. [Google Scholar] [CrossRef]
- Marandi, A.; Zarei-Hanzaki, R.; Zarei-Hanzaki, A.; Abedi, H.R. Dynamic recrystallization behavior of new transformation–twinning induced plasticity steel. Mater. Sci. Eng. A 2014, 607, 397–408. [Google Scholar] [CrossRef]
- Zangeneh Najafi, S.; Momeni, A.; Jafarian, H.R.; Ghadar, S. Recrystallization, precipitation and flow behavior of D3 tool steel under hot working condition. Mater. Charact. 2017, 132, 437–447. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- McQueen, H.J.; Ryan, N.D. Constitutive analysis in hot working. Mater. Sci. Eng. A 2002, 322, 43–63. [Google Scholar] [CrossRef]
- McQueen, H.J.; Yue, S.; Ryan, N.D.; Fry, E. Hot working characteristics of steels in austenitic state. J. Mater. Process. Technol. 1995, 53, 293–310. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Bergstrom, Y. A Dislocation Model for the Stress-strain behaviour of polycrystalline a-fe with special emphasis on the variation of the densities of mobile and immobile dislocations. Mater. Sci. Eng. 1969, 5, 193–200. [Google Scholar] [CrossRef]
- Bergitrom, Y. The Plastic Deformation of Metals—A dislocation model and its applicability. Rev. Powder Metall. Phys. Ceram. 1983, 2, 79–265. [Google Scholar]
- Hamada, A.S.; Khosravifard, A.; Kisko, A.P.; Ahmed, E.; Porter, D.A. High temperature deformation behavior of a stainless steel fiber-reinforced copper matrix composite. Mater. Sci. Eng. A 2016, 669, 469–479. [Google Scholar] [CrossRef]
- Jonas, J.J.; Quelennec, X.; Jiang, L.; Martin, É. The Avrami kinetics of dynamic recrystallization. Acta Mater. 2009, 57, 2748–2756. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, L.; Xu, Q.; Xia, Y.; Shen, W. The kinetics and cellular automaton modeling of dynamic recrystallization behavior of a medium carbon Cr-Ni-Mo alloyed steel in hot working process. Mater. Sci. Eng. A 2016, 678, 33–43. [Google Scholar] [CrossRef]
- Haghdadi, N.; Martin, D.; Hodgson, P. Physically-based constitutive modelling of hot deformation behavior in a LDX 2101 duplex stainless steel. Mater. Des. 2016, 106, 420–427. [Google Scholar] [CrossRef]
- El Wahabi, M.; Cabrera, J.M.; Prado, J.M. Hot working of two AISI 304 steels: A comparative study. Mater. Sci. Eng. A 2003, 343, 116–125. [Google Scholar] [CrossRef]
- Dong, J.; Li, C.; Liu, C.; Huang, Y.; Yu, L.; Li, H.; Liu, Y. Hot deformation behavior and microstructural evolution of Nb–V–Ti microalloyed ultra-high strength steel. J. Mater. Res. 2017, 32, 3777–3787. [Google Scholar] [CrossRef]
- Qin, F.; Zhu, H.; Wang, Z.; Zhao, X.; He, W.; Chen, H. Dislocation and twinning mechanisms for dynamic recrystallization of as-cast Mn18Cr18N steel. Mater. Sci. Eng. A 2017, 684, 634–644. [Google Scholar] [CrossRef]
- Sun, H.; Sun, Y.; Zhang, R.; Wang, M.; Tang, R.; Zhou, Z. Hot deformation behavior and microstructural evolution of a modified 310 austenitic steel. Mater. Des. 2014, 64, 374–380. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, M.; Wu, H.; Yang, B. Study on the dynamic recrystallization model and mechanism of nuclear grade 316LN austenitic stainless steel. Mater. Charact. 2016, 118, 92–101. [Google Scholar] [CrossRef]
- Parthiban, R.; Ghosh Chowdhury, S.; Harikumar, K.C.; Sankaran, S. Evolution of microstructure and its influence on tensile properties in thermo-mechanically controlled processed (TMCP) quench and partition (Q&P) steel. Mater. Sci. Eng. A 2017, 705, 376–384. [Google Scholar] [CrossRef]










| Symbols | Parameters |
|---|---|
| A | Material constant () |
| AARE | Average absolute relative error |
| k | Material constant |
| M | Dislocation strengthening constant |
| n | Stress exponent |
| nA | Avrami’s exponent |
| Q | Activation energy for hot deformation () |
| R | Universal gas constant () |
| T | Absolute deformation temperature () |
| U | Hardening parameter () |
| X | Recrystallized volume fraction |
| Z | Zener–Hollomon parameter () |
| Stress multiplier () | |
| Austenite phase | |
| True strain | |
| Strain rate () | |
| μ | Shear modulus () |
| ρ | Dislocation density () |
| True stress () | |
| Lattice friction stress () | |
| Peak stress () | |
| Steady state stress after dynamic recrystallization () | |
| Ω | Softening parameter |
| Sample | Q, kJ/mol | n | A, s−1 | , MPa−1 |
|---|---|---|---|---|
| Ti-Mo | 428.5 | 5.00 | 1.69 × 1016 | 0.009876 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Cai, M.; Yang, P.; Su, J.; Guo, X. Physically-Based Modeling and Characterization of Hot Flow Behavior in an Interphase-Precipitated Ti-Mo Microalloyed Steel. Metals 2018, 8, 243. https://doi.org/10.3390/met8040243
Wu C, Cai M, Yang P, Su J, Guo X. Physically-Based Modeling and Characterization of Hot Flow Behavior in an Interphase-Precipitated Ti-Mo Microalloyed Steel. Metals. 2018; 8(4):243. https://doi.org/10.3390/met8040243
Chicago/Turabian StyleWu, Chuanfeng, Minghui Cai, Peiru Yang, Junhua Su, and Xiaopeng Guo. 2018. "Physically-Based Modeling and Characterization of Hot Flow Behavior in an Interphase-Precipitated Ti-Mo Microalloyed Steel" Metals 8, no. 4: 243. https://doi.org/10.3390/met8040243
APA StyleWu, C., Cai, M., Yang, P., Su, J., & Guo, X. (2018). Physically-Based Modeling and Characterization of Hot Flow Behavior in an Interphase-Precipitated Ti-Mo Microalloyed Steel. Metals, 8(4), 243. https://doi.org/10.3390/met8040243