Growth Morphologies and Primary Solidification Modes in a Dissimilar Weld between a Low-Alloy Steel and an Austenitic Stainless Steel
Abstract
:1. Introduction
- (1)
- to investigate the evolutions of composition, morphology, microstructure, and solidification mode near the fusion boundary of a single-pass weld produced by SAW between the 18MND5 low-alloy steel (similar to ASTM A533 grade B or DIN 1.6308) and the 309L stainless steel;
- (2)
- to evaluate from these data the local values of the solidification parameters (G, V);
- (3)
- to discuss the mechanisms responsible for the selection of the primary solidification phase observed at the fusion line by questioning the melting behavior of the base metal;
- (4)
- to use thermokinetic computations and the solidification model for explaining the transitions in solidification mode and predict their location in the welded joint.
2. Materials and Methods
2.1. Base Materials and Weld Production
2.2. Characterization of Composition and Microstructure
2.3. Thermodynamic Calculations
3. Results
3.1. Evolution of Composition and Microstructure through the Weld
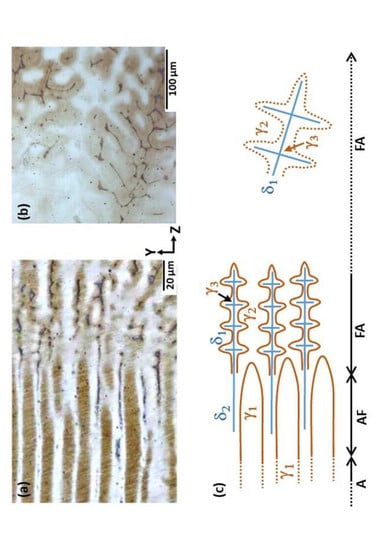
3.2. Morphological Evolution and Change in the Solidification Mode
- (1)
- A mode: Liquid→γ1
- (2)
- AF mode: Liquid→γ1, followed by Liquid→γ1 + δ2
- (3)
- FA mode: Liquid→δ1, followed by Liquid→γ2 and by δ1→γ3 during cooling.
3.3. Orientation Relationship between Base and Weld Metals
4. Discussion
4.1. Solidification Conditions at the Plane Front to Cell Transition
4.2. Origin of the Purely Austenitic Zone
- (1)
- Liquid→δ
- (2)
- Liquid + δ→γ until ferrite disappears
- (3)
- Liquid→γ
4.3. Formation of Ferrite in the Inter-Cellular Space
4.4. Growth Competition between Ferrite and Austenite
5. Conclusions
- Transitions between planar, cellular, and dendritic morphologies were observed as predicted by the increasing growth rate when moving away from the fusion line.
- Close to the fusion boundary the order of magnitude of the growth rate (~175 µm·s−1) and thermal gradient (~4 × 106 K·m−1) were estimated at the plane front to cells transition. The present approach combining microstructural observations, thermodynamic and kinetic data, and the constitutional supercooling criterion can be successfully used for determining those important pieces of data useful for the validation of numerical modelling of welding processes.
- The selection of non-equilibrium austenite as primary phase during the initial transient period of plane front growth was assigned to its epitaxial growth on the entirely austenitic structure of the 18MND5 substrate at the fusion line resulting from an incipient melting mechanism. This interpretation is supported both by (i) the clear correspondence between the corrugated shape of the fusion line and the observed phantom of the dendritic network of the cast 18MND5 ingot and (ii) by thermodynamic computations considering the segregation of solutes during solidification of the 18MND5 ingot.
- The first change in the solidification mode (A→AF) with ferrite forming in between the austenite cells was accurately predicted by computations of non-equilibrium solidification paths considering the evolution of the liquid composition in the partially mixed zone.
- The last transition (AF→FA) was assigned to the faster growth of ferrite (once nucleated) compared to austenite, as confirmed by use of a classical model of columnar dendritic growth.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ornath, F.; Soudry, J.; Weiss, B. Weld pool segregation during the welding of low alloy steels with austenitic electrodes. Weld. J. Weld. Res. Suppl. 1981, 60, 227s–230s. [Google Scholar]
- Nelson, T.W.; Lippold, J.C.; Mills, M.J. Investigation of boundaries and structures in dissimilar metal welds. Sci. Technol. Weld. Join. 1998, 3, 249–255. [Google Scholar] [CrossRef]
- Nelson, T.W.; Lippold, J.C.; Mills, M.J. Nature and evolution of the fusion boundary in ferritic-austenitic dissimilar metal welds. Part 1—Nucleation and growth. Weld. J. Weld. Res. Suppl. 1999, 78, 329s–337s. [Google Scholar]
- Nelson, T.W.; Lippold, J.C.; Mills, M.J. Nature and evolution of the fusion boundary in ferritic-austenitic dissimilar metal welds. Part 2—On-cooling transformations. Weld. J. Weld. Res. Suppl. 2000, 79, 267s–277s. [Google Scholar]
- Rowe, M.D.; Nelson, T.W.; Lippold, J.C. Hydrogen-induced cracking along the fusion boundary of dissimilar metal welds. Weld. J. Weld. Res. Suppl. 1999, 78, 31s–37s. [Google Scholar]
- Arivazhagan, N.; Singh, S.; Prakash, S.; Reddy, G.M. Investigation on AISI 304 austenitic stainless steel to AISI 4140 low alloy steel dissimilar joints by gas tungsten arc, electron beam and friction welding. Mater. Des. 2011, 32, 3036–3050. [Google Scholar] [CrossRef]
- Brentrup, G.J.; DuPont, J.N. Fabrication and characterization of graded transition joints for welding dissimilar alloys. Weld. J. Weld. Res. Suppl. 2013, 92, 72s–79s. [Google Scholar]
- Hajiannia, I.; Shamanian, M.; Kasiri, M. Microstructure and mechanical properties of AISI 347 stainless steel/A335 low alloy steel dissimilar joint produced by gas tungsten arc welding. Mater. Des. 2013, 50, 566–573. [Google Scholar] [CrossRef]
- Ahmad, H.W.; Hwang, J.H.; Lee, J.H.; Bae, D.H. An assessment of the mechanical properties and microstructural analysis of dissimilar material welded joint between alloy 617 and 12Cr steel. Metals 2016, 6, 242. [Google Scholar] [CrossRef]
- DuPont, J.N.; Mizia, R.E. Review of Dissimilar Metal Welding for the NGNP Helical-Coil Steam Generator; INL Report; EXT-10-18459; Idaho National Laboratory: Idaho Falls, ID, USA, 2010; pp. 1–68.
- Babu, S.S.; Elmer, J.W.; Vitek, J.M.; David, S.A. Time-resolved X-ray diffraction investigation of primary weld solidification in Fe-C-Al-Mn steel welds. Acta Mater. 2002, 50, 4763–4781. [Google Scholar] [CrossRef]
- Cui, Y.; Xu, C.; Han, Q. Effect of ultrasonic vibration on unmixed zone formation. Scr. Mater. 2006, 55, 975–978. [Google Scholar] [CrossRef]
- Joarder, A.; Saha, S.C.; Ghose, A.K. Study of submerged arc weld metal and heat-affected zone microstructures of a plain carbon steel. Weld. J. Weld. Res. Suppl. 1991, 70, 141s–146s. [Google Scholar]
- McPherson, N.A.; Baker, T.N.; Millar, D.W. A study of the structure of dissimilar submerged arc welds. Metall. Mater. Trans. A 1998, 29, 823–832. [Google Scholar] [CrossRef]
- McPherson, N.A.; Chi, K.; McLean, M.S.; Baker, T.N. Structure and properties of carbon steel to duplex stainless steel submerged arc welds. Mater. Sci. Technol. 2003, 19, 219–226. [Google Scholar] [CrossRef]
- Taban, E.; Deleu, E.; Dhooge, A.; Kaluc, E. Evaluation of Dissimilar Welds between Ferritic Stainless Steel Modified 12% Cr and Carbon Steel S355. Weld. J. Weld. Res. Suppl. 2008, 87, 291s–297s. [Google Scholar]
- Sirin, K.; Sirin, S.Y.; Kaluc, E. Influence of the chemical composition of weld electrode on the mechanical properties of submerged arc welded pipe. Int. J. Adv. Manuf. Technol. 2016, 87, 1941–1950. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, M.; Liu, W.; Wei, X.; Xu, J.; Chen, J.; Lu, H.; Yu, C. Study of type-II boundary behavior during SA508-3/EQ309L overlay weld interfacial failure process. J. Mater. Proc. Technol. 2017, 247, 64–72. [Google Scholar] [CrossRef]
- Savage, W.; Nippes, E.; Szekeres, E. A study of weld interface phenomena in a low-alloy steel. Weld. J. Weld. Res. Suppl. 1976, 55, 260s–268s. [Google Scholar]
- Ishida, T. Formation of stainless steel layer on mild steel by welding arc cladding. J. Mater. Sci. 1991, 26, 6431–6435. [Google Scholar] [CrossRef]
- Doody, T. Intermediate mixed zone in dissimilar metal welds for sour service. Weld. J. Weld. Res. Suppl. 1992, 55, 55s–60s. [Google Scholar]
- Kou, S.; Yang, Y. Fusion-boundary macrosegregation in dissimilar-filler welds. Weld. J. Weld. Res. Suppl. 2007, 86, 303s–312s. [Google Scholar]
- DuPont, J.; Kusko, C. Technical note: Martensite formation in austenitic/ferritic dissimilar alloy welds. Weld. J. Weld. Res. Suppl. 2007, 86, 51s–54s. [Google Scholar]
- David, S.; Vitek, J. Correlation between solidification parameters and weld microstructures. Int. Mater. Rev. 1989, 34, 213–245. [Google Scholar] [CrossRef]
- Kou, S. Welding Metallurgy, 2nd ed.; John Wiley & Sons: Hobken, NJ, USA, 2003; pp. 226–231. ISBN 0-471-43491-4. [Google Scholar]
- DuPont, J.N. Fundamentals of weld solidification. In ASM Handbook 6A, Welding Fundamentals and Processes; ASM International: Metals Park, OH, USA, 2011; pp. 96–114. [Google Scholar]
- Elmer, J.W. A new path forward for understanding microstructural evolution during welding. Weld. J. Weld. Res. Suppl. 2008, 87, 149s–166s. [Google Scholar]
- Pan, C.; Wang, R.; Gui, J.; Shi, Y. Direct TEM observation of microstructures of the austenitic/carbon steels welded joint. J. Mater. Sci. 1990, 25, 3281–3285. [Google Scholar] [CrossRef]
- Gauzzi, F.; Missori, S. Microstructural transformations in austenitic-ferritic transition joints. J. Mater. Sci. 1988, 23, 782–789. [Google Scholar] [CrossRef]
- Huang, M.L.; Wang, D.L. Carbon migration in 5Cr-0.5 Mo/21Cr-12Ni dissimilar metal welds. Metall. Mater. Trans. A 1998, 29, 3037–3046. [Google Scholar] [CrossRef]
- Mas, F.; Tassin, C.; Valle, N.; Robaut, F.; Charlot, F.; Yescas, M.; Roch, F.; Todeschini, P.; Bréchet, Y. Metallurgical characterization of coupled carbon diffusion and precipitation in dissimilar steel welds. J. Mater. Sci. 2016, 51, 4864–4879. [Google Scholar] [CrossRef]
- Mas, F.; Martin, G.; Lhuissier, P.; Bréchet, Y.; Tassin, C.; Roch, F.; Todeschini, P.; Simar, A. Heterogeneities in local plastic flow behavior in a dissimilar weld between low-alloy steel and stainless steel. Mater. Sci. Eng. A 2016, 667, 156–170. [Google Scholar] [CrossRef]
- Wu, Y.; Patchett, B.M. Formation of crack-susceptible structures of weld overlay of corrosion resistant alloys. Mater. Perform. Sulphur Energy 1992, 283–295. [Google Scholar]
- Murugan, N.; Gunaraj, V. Prediction and control of weld bead geometry and shape relationships in submerged arc welding of pipes. J. Mater. Proc. Technol. 2005, 168, 478–487. [Google Scholar] [CrossRef]
- Cho, D.W.; Song, W.H.; Cho, M.H.; Na, S.J. Analysis of submerged arc welding process by three-dimensional computational fluid dynamics simulations. J. Mater. Proc. Technol. 2013, 213, 2278–2291. [Google Scholar] [CrossRef]
- Winczek, J.; Gawronska, E. The modeling of heat affected zone (HAZ) in submerged arc welding (SAW) surfacing steel element. Metabk 2016, 55, 225–228. [Google Scholar]
- Cayron, C.; Artaud, B.; Briottet, L. Reconstruction of Parent Grains from EBSD Data. Mater. Charact. 2006, 57, 386–401. [Google Scholar] [CrossRef]
- Cayron, C. ARPGE: A computer program to automatically reconstruct the parent grains from electron backscatter diffraction data. J. Appl. Cryst. 2007, 40, 1183–1188. [Google Scholar] [CrossRef]
- Andersson, J.O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc and DICTRA, Computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar] [CrossRef]
- Anderson, T.D.; Perricone, M.J.; Dupont, J.N.; Marder, A.R. The influence of molybdenum on stainless steel weld microstructures. Weld. J. Weld. Res. Suppl. 2007, 86, 281s–292s. [Google Scholar]
- Cayron, C. GenOVa: A computer program to generate orientational variants. J. Appl. Cryst. 2007, 40, 1179–1182. [Google Scholar] [CrossRef]
- Greninger, A.B.; Troiano, A.R. The mechanism of martensite formation. Metall. Trans. 1949, 1, 590–598. [Google Scholar] [CrossRef]
- Kurdjumov, G.; Sachs, G. Über den Mechanismus der Stahlhärtung. Z. Für Phys. 1930, 64, 325–343. [Google Scholar] [CrossRef]
- Nishiyama, Z. X-ray investigation of the mechanism of transformation from face-centered-cubic lattice to body-centered cubic. Sci. Rep. Tohoku. Univ. 1934, 23, 637–664. [Google Scholar]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification, 3rd ed.; Trans Tech Publications: Zürich, Switzerland, 1989; pp. 45–61. ISBN 0-87849-522-3. [Google Scholar]
- Dantzig, J.A.; Rappaz, M. Solidification, 1st ed.; EPFL Press: Lausanne, Switzerland, 2009; pp. 451–452. ISBN 978-2-940222-17-9. [Google Scholar]
- Tiller, W.A.; Jackson, K.A.; Rutter, J.W.; Chalmers, B. The redistribution of solute atoms during the solidification of metals. Acta. Metall. 1953, 1, 428–437. [Google Scholar] [CrossRef]
- Coates, D.E.; Subramanian, S.V.; Purdy, G.R. Solid-liquid interface stability during solidification of dilute ternary alloys. Trans. AIME 1968, 242, 800–809. [Google Scholar]
- Katayama, S.; Matsunawa, A. Solidification microstructure of laser welded stainless steels. In Proceedings of the International Congress on Applications of Lasers & Electro-Optics (ICALEO), Boston, MA, USA, 12–15 November 1968; Publ. Laser Institute of America: Orlando, FL, USA, 1968; pp. 60–67. [Google Scholar]
- Elmer, J.W.; Allen, S.M.; Eager, T.W. Microstructural development during solidification of stainless steel alloys. Metall. Trans. A 1989, 20, 2117–2131. [Google Scholar] [CrossRef]
- Ikawa, H.; Shin, S.; Inui, M.; Takeda, Y.; Nakano, A. On the martensitic-like structure at weld bond and the macroscopic segregation in weld metal in the welded dissimilar metals of α−steels and γ−steels. IIW Database 1972, IIW Doc IX-785-72, 1–32. [Google Scholar]
- Kurz, W.; Giovanola, B.; Trivedi, R. Theory of microstructural development during rapid solidification. Acta. Metall. 1986, 34, 823–830. [Google Scholar] [CrossRef]
- Ha, H.P.; Hunt, J.D. An experimental and theoretical study of the peritectic reaction. In Proceedings of the 4th Decennial International Conference on Solidification Processing, Sheffield, UK, 7–10 July 1997; Beech, J., Jones, H., Eds.; pp. 444–448. [Google Scholar]
- Vandyoussefi, M.; Kerr, H.W.; Kurz, W. Solidification microstructure selection map for Fe-Ni peritectic alloys. In Proceedings of the 4th Decennial International Conference on Solidification Processing, Sheffield, UK, 7–10 July 1997; Beech, J., Jones, H., Eds.; pp. 564–567. [Google Scholar]
- Hunziker, O.; Vandyoussefi, M.; Kurz, W. Phase and microstructure selection in peritectic alloys close to the limit of constitutional undercooling. Acta Mater. 1998, 46, 6325–6336. [Google Scholar] [CrossRef]
- Fukumoto, S.; Okane, T.; Umeda, T.; Kurz, W. Crystallographic relationships between δ-ferrite and γ-austenite during unidirectional solidification of Fe-Cr-Ni alloys. ISIJ Int. 2000, 40, 677–684. [Google Scholar] [CrossRef]
- Rettenmayr, M. Melting and remelting phenomena. Int. Mater. Rev. 2009, 54, 1–17. [Google Scholar] [CrossRef]
- Han, Q.; Hellawell, H. Primary particle melting rates and equiaxed solidification. Metall. Mater. Trans. B 1997, 28, 169–173. [Google Scholar] [CrossRef]
- Bobadilla, M.; Lacaze, J.; Lesoult, G. Influence des conditions de solidification sur le déroulement de la solidification des aciers inoxydables austénitiques. J. Cryst. Growth. 1988, 89, 531–544. [Google Scholar] [CrossRef]
- Fukumoto, S.; Kurz, W. The δ to γ transition in Fe-Cr-Ni alloys during laser treatment. ISIJ Int. 1997, 7, 677–684. [Google Scholar] [CrossRef]
- Fukumoto, S.; Kurz, W. Prediction of the δ to γ transition in austenitic stainless steels during laser treatment. ISIJ Int. 1998, 38, 71–77. [Google Scholar] [CrossRef]
- Babu, S.S.; Vitek, J.M.; Elmer, J.W.; Palmer, T.A.; David, S.A. Nonequilibrium phase selection during weld solidification of Fe-C-Mn-Al. In Solidification Processes and Microstructures: A Symposium in Honor of Wilfried Kurz; Wiley: New York, NY, USA, 2004; pp. 339–344. [Google Scholar]
- Hashimoto, T.; Terasaki, H.; Komizo, Y. Effect of solidification velocity on weld solidification process of alloy tool steel. Sci. Technol. Weld. Join. 2008, 13, 409–414. [Google Scholar] [CrossRef]
- Rappaz, M.; David, S.A.; Vitek, J.M.; Boatner, L.A. Analysis of solidification microstructures in Fe-Ni-Cr single-crystal welds. Metall. Trans. A 1990, 21, 1767–1782. [Google Scholar] [CrossRef]
- Siredey, N.; Lacaze, J. Growth conditions at the solidification front of multicomponent alloys. Scr. Metall. Mater. 1993, 29, 759–764. [Google Scholar] [CrossRef]
- Ivantsov, G.P. Temperature field around a spherical, cylindrical, and needle-shaped crystal, growing in a pre-cooled melt. Dokl. Akad. Nauk. SSSR 1947, 58, 567–569. [Google Scholar]
- Mullins, W.W.; Sekerka, R.F. Stability of a planar interface during solidification of a dilute binary alloy. J. Appl. Phys. 1964, 35, 444–451. [Google Scholar] [CrossRef]













| Materials | C | Cr | Mn | Mo | N | Ni | Si | Fe |
|---|---|---|---|---|---|---|---|---|
| 18MND5 Base metal | 0.18 | 0.2 | 1.4 | 0.3 | 0.009 | 0.7 | 0.4 | bal. |
| 309L Filler metal | 0.021 | 23.7 | 1.7 | 0.07 | 0.039 | 12.6 | 0.36 | bal. |
| Welding Parameters | Data |
|---|---|
| Polarity | + at the strip electrode |
| Voltage (V) | 27 |
| Intensity (A) | 750 ± 20 |
| Travel speed (cm·min−1) | 13.5–14.5 |
| Stick-out (mm) | 28 |
| Strip angle (°) | 90 |
| Pre-heating temperature (°C) | 130 |
| Z (mm) | 0 | 20 | 50 | 100 | 300 |
|---|---|---|---|---|---|
| VZ (µm·s−1) | 0 | 175 | 440 | 560 | 650 |
| Primary Phase | k (Cr) | k (Ni) | Liquidus (°C) |
|---|---|---|---|
| FCC (face-centered cubic) austenite | 0.86 | 1.0 | 1440 |
| BCC (body-centered cubic) ferrite | 1.03 | 0.76 | 1452 |
| Thermo-Kinetic Parameters | Symbols | Data |
|---|---|---|
| Inter-diffusion coefficient of Cr in the liquid | D11 | 1.5 × 10−9 m2·s−1 |
| Inter-diffusion coefficient of Ni in the liquid | D22 | 1.5 × 10−9 m2·s−1 |
| Nominal composition in Cr | 6.1 wt. % | |
| Nominal composition in Ni | 3.3 wt. % | |
| Liquidus slope for Cr | m1 | −300 K (wt. %)−1 |
| Liquidus slope for Ni | m2 | −155 K (wt. %)−1 |
| Liquidus temperature | TL | 1780 K |
| Mass partition coefficient of Cr | k1 | 0.87 |
| Mass partition coefficient of Ni | k2 | 0.93 |
| Thermo-Kinetic Parameters | Symbols | Ferrite (Φ = δ) | Austenite (Φ = γ) |
|---|---|---|---|
| Liquidus temperature (K) | TLΦ | 1745 | 1736 |
| Liquidus slope for Cr (K/wt. %) | mΦCr | −0.75 | −4.18 |
| Liquidus slope for Ni (K/wt. %) | mΦNi | −5.8 | −0.78 |
| Liquidus slope for C (K/wt. %) | mΦC | −108.5 | −58.5 |
| Partition coefficient of Cr | kCr | 1 | 0.85 |
| Partition coefficient of Ni | kNi | 0.78 | 1 |
| Partition coefficient of C | kC | 0.12 | 0.34 |
| Interdiffusion coefficient in the liquid (m2·s−1) | D | 1.5 × 10−9 | 1.5 × 10−9 |
| Solid/liquid interfacial energy (J·m−2) | 0.260 | 0.358 | |
| Molar volume at liquidus temperature (m3·mol−1) | Vm | 7.52 × 10−6 | 9.03 × 10−6 |
| Molar entropy of fusion (J·mol−1·K−1) | 5.79 | 6.63 | |
| Thermal conductivity (J·s−1·m−1·K−1) | κ | 30 | 27 |
| Gibbs Thomson coefficient (m·K) | Γ | 3.39 × 10−7 | 4.87 × 10−7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mas, F.; Tassin, C.; Roch, F.; Yescas, M.; Todeschini, P.; Bréchet, Y. Growth Morphologies and Primary Solidification Modes in a Dissimilar Weld between a Low-Alloy Steel and an Austenitic Stainless Steel. Metals 2018, 8, 284. https://doi.org/10.3390/met8040284
Mas F, Tassin C, Roch F, Yescas M, Todeschini P, Bréchet Y. Growth Morphologies and Primary Solidification Modes in a Dissimilar Weld between a Low-Alloy Steel and an Austenitic Stainless Steel. Metals. 2018; 8(4):284. https://doi.org/10.3390/met8040284
Chicago/Turabian StyleMas, Fanny, Catherine Tassin, François Roch, Miguel Yescas, Patrick Todeschini, and Yves Bréchet. 2018. "Growth Morphologies and Primary Solidification Modes in a Dissimilar Weld between a Low-Alloy Steel and an Austenitic Stainless Steel" Metals 8, no. 4: 284. https://doi.org/10.3390/met8040284
APA StyleMas, F., Tassin, C., Roch, F., Yescas, M., Todeschini, P., & Bréchet, Y. (2018). Growth Morphologies and Primary Solidification Modes in a Dissimilar Weld between a Low-Alloy Steel and an Austenitic Stainless Steel. Metals, 8(4), 284. https://doi.org/10.3390/met8040284