Evaluating the Effect of External Horizontal Fixed Shading Devices’ Geometry on Internal Air Temperature, Daylighting and Energy Demand in Hot Dry Climate. Case Study of Ghardaïa, Algeria

Abstract

The present study investigates the effect of fixed external shading devices’ geometry on thermal comfort, daylighting and energy demand for cooling and heating in the hot and dry climate of the city of Ghardaïa (Algeria). A parametric analysis was performed by using three software: RADIANCE 2.0 and DAYSIM 3.1 for daylighting simulation and TRNSYS.17 for thermal dynamic simulation. Three shading device parameters were assessed: the spacing between slats, the tilted angle and the slats installation. The vertical shading angle “VSA” is fixed; it is equal to the optimum shading angle measured for Ghardaïa. The simulation results indicate that fixed external shading devices have a significant impact on decreasing the energy demand for cooling; however, they are unable to reduce the total energy demand since they significantly increase heating loads. It was found that fixed external shading devices remove all risks associated with glare in summer by decreasing illuminance close to the window; however, they do not improve daylighting performance in winter because of glare. We note that even if the vertical shading angle “VSA” was the same for all cases, these did not present the same thermal and luminous behavior. This is mainly due to the amount and the way that the solar radiation penetrates space.

1. Introduction

Solar protection is a passive strategy that directly influences thermal and visual comfort as well as heating, cooling and lighting energy consumption. Using shading devices can produce some conflicts such as contradiction between winter requirements, summer comfort and luminous comfort [1]. This is why the shading device choice is a necessary issue for building design, especially in a hot and dry climate. An optimal solar protection must provide a maximum protection during the overheating period, while permitting solar radiation penetration during the winter [2].

Many researchers have studied the effect of shading devices on thermal comfort, especially in a cold climate; Datta conducted a study for four different cities in Italy [3] and Tzempelikos et al. [4,5,6] performed an experimental study of the indoor thermal environment with different types of shading devices under Montreal climatic conditions in winter. Other studies were carried out in hot climate regions to evaluate fixed shading devices [7,8,9] and dynamic ones [10].

Certain studies focused on shading devices’ effect on indoor factors; Dubois evaluated the daylight quality of shading devices [11]. Wong et al. studied the effect of external shading devices on daylighting penetration [12]. Freewan et al. [13] investigated the impact of ceiling geometries on the performance of louvers using two performance indicators: the illuminance level and its distribution uniformity. Datta [3] and Bessoudo et al. [6] evaluated the shading devices’ effect on the thermal performance of building.

Several studies focused on energy consumption. Kim et al. [14] studied the external shading device effect in terms of energy savings for heating and cooling. Al Touma and Ouahrani [9,15] conducted a study on shading and daylighting controls energy savings in offices with fully glazed façades in hot climates. Ossen et al. [8] studied the impact of solar shading geometry on building energy use in hot humid climates. Palmero-Marrero and Oliveira [16] studied the effect of louver shading devices on building energy requirements. Cillari et al. [17] analyzed the effects of the integration of different passive systems’ energy demand for cooling and heating and showed that fixed shadings led only to 1.28% energy saving in cooling and an increase in energy demand for heating by 0.46%. Hammad [10] demonstrated that the optimal static angle is −20° (i.e., 70° to the vertical) that resulted in a 31.36% reduction in energy consumption, which is about 34.02 for the dynamic facade.

Other studies explored both the luminous and thermal effect [1,7,18,19]. Alzoubi et al. [20] assessed vertical and horizontal shading devices’ performance in terms of daylighting and consumption; Vera et al. [21] focused on the optimization process of a shading device composed of curved and perforated fixed louvers, considering the visual comfort and energy consumption criteria. Kim [22] performed a series of simulations and measurements to evaluate the daylighting, energy and view performance of shading devices. Nielsen et al. [23] studied the daylight and energy saving potential of automated dynamic solar shading in office buildings.

Settino et al. [24] performed a multi-objective analysis of fixed external solar shading systems with the aim of minimizing the energy consumption for heating, cooling and artificial lighting, while ensuring the visual comfort of the occupants, showing that the use of an optimal shading configuration allows a reduction in the annual energy consumption of up to 42%. The impact of several design parameters was studied, such as:

• The ratio between slats vertical distance and their width $\frac{s}{l}$: Datta [6] studied three values of $\frac{s}{l}$ (1, 2 and 0.92). Ouahrani and Al Touma [15] found that, for south orientation, a slat separation-to-width ratio of less than one ($\frac{s}{l}<1$) saves between 27.6% and 35.0% of the space total energy demand, eliminates glare visual discomfort and reduces CO₂ emissions.
• The spacing between the slats: Oliveira [16] conducted a study of shading devices with a spacing of 0.23 m and 0.26 m depending on latitude. Hammad [10] from the United Arab Emirates set the spacing at 0.3 m and Alzoubi [20] from Jordan studied the case of spacing of 0.5 m; in both studies, the ratio s/l was equal to one, i.e., the vertical shading angle was 45°. In the United Kingdom, Freewan [13] fixed the $\frac{s}{l}$ ratio to the same value and spacing between the slats was fixed at 0.05 m.
• The tilted angle: In a previous study [1], the effect of three tilted angles (60°, 90° and 120°) on luminous and thermal conditions within spaces in hot climates was investigated. Hammad [10] and Alzoubi [20] both show that the total annual energy consumption and lighting level changes in correlation with the tilted angle of slats. Al Touma and Ouahrani [9] studied the impact of two tilted angles (45° and 90°) for north and south orientations. It was found that a tilted angle of 45° reduces energy demand by 7.7% and 18.6% for south and north-oriented offices, respectively; however, a tilted angle of 90° leads to 9.1% and 20.6% energy savings.
• Freewan [7] also carried out a comparative study on different types of shading devices (vertical fins, diagonal fins and an egg crate) where he varied several parameters: width of fins, spacing and tilted angle. Ossen et al. [8] studied the impact of solar shading geometry on building energy use in a hot humid climate.

Studies on shading devices used different tools, such as the dynamic computer simulation program eQUEST-3 (DOE 2.2) developed by James J. Hirsch & Associates (JJH) in collaboration with Lawrence Berkeley National Laboratory (LBNL) [8], Desktop Radiance software developed by the Building Technologies Department of the Environmental Energy Technologies Division at the Berkeley Lab [7], TRNSYS software developed by Thermal Energy System Specialists [3,13] IES/SunCast and the IES Virtual Environment (IES VE) programs developed by Integrated Environmental Solutions Ltd. [14,25].

Previous studies have shown that shading devices could significantly reduce energy used for cooling and lighting by reducing air temperature and controlling illuminance without glare. However, they have a negative impact on heating loads because they reduce useful solar gains during the winter [26,27].

Most studies considered the Vertical Shading Angle (VSA) as a variable parameter, which changes according to the spacing between slats and their width, which means that shading either is not optimal during the overheating period or there is no sunshine in cold periods. This paper resumes a part of our PhD research on luminous and thermal performance of shading devices, where we fixed the VSA that is equal to the optimum shading angle measured from the latitude and the climatic data of our case study (the city of Ghardaïa). Shading device design parameters considered are the vertical spacing between slats, tilted angle and their installation.

We aim to evaluate, through a parametric study, the thermal and luminous effects of these variables. The objective is to verify the fixed shading devices’ effect on thermal, daylight and energy performance. We investigate the performance of fixed external shading devices in the dry and hot climate of Ghardaïa, a southern Algerian city. In this paper, only results for the south orientation are presented.

2. Methodology

2.1. Study Area

The simulations were performed for Ghardaïa, Algeria (Latitude: 32.23° N, Longitude: 3.49° E, Altitude: 450 m), according to the Köppen–Geiger climate classification; Ghardaïa is characterized by a hot desert climate (Bwh) [28]. Recorded average temperatures ranged from 6 °C in January to 40 °C in July. Humidity values, ranging between 25% and 60%, were inversely proportional to air temperatures: maximum in winter (January–December), minimal in summer (August–July) [29]. Average daily global solar irradiation varied between 3500 Wh/m² and 7900 Wh/m², with the highest value recorded in July [30]. In sunniest month (July), the average daily direct irradiation was about 6.1 kWh/m² and less than 30% of the radiation was diffuse. In December, the average daily direct irradiation was around 2.2 kWh/m² and about 40% was diffuse radiation (Figure 1).

Prevailing winds were of north and northwest direction in winter (14.53% and 10.44%, respectively) and northeast in summer (12.44%). Strong, cold and relatively humid in winter, they were hot and dry in summer. The mean speed was 3.9 m/s [29].

2.2. Case Study Description

Simulation work was carried out on the room shown in Figure 2 with dimensions 6 m × 4 m × 3 m. South-facing façade was selected for simulation. Fenestration area was 3.6 m², i.e., 30% window-to-wall ratio and 15% window-to-floor ratio. The room was modeled as a separate zone and no external obstructions were taken into account. The surface reflectance was 80%, 60% and 40% for ceiling, vertical walls and floor were 80%, 60% and 40%, respectively. Building envelope characteristics are presented in Section 2.4. Simulation Tools and Conditions.

2.3. Sizing of Shading Devices and Geometries

Optimal shading devices depends on the location (latitude) and air temperature in which they had to be used. It also depended on the size and orientation of the window to protect. Figure 3 shows Ghardaïa overheating period, which corresponded to air temperatures above 27 °C. This period was from May to September. Then, the overheating period was reported on the solar diagram corresponding to the latitude of Ghardaïa (32.23° N).

The optimal upper and lower shading angles were calculated using the shadow angle protractor; these angles defined the upper and lower limits of shading devices. For the south orientation, the optimal upper and lower vertical shading angles were, respectively, equal to 82° and 57° (Figure 4). Alternatively, the vertical shading angle could be calculated using the following equations [31]:

$$\mathrm{VSA}={\tan }^{-1}\left[\left(\tan ALT\right)/\cos HSA\right]$$

(1)

HSA = AZ − θ

(2)

where:

• ALT: Altitude angle.
• VSA: Vertical shading angle.
• HSA: Horizontal shading angle.
• AZ: Azimuth.
• θ: Facade orientation.

Design parameters for external shading devices are graphically presented in Figure 5, and using the optimal lower vertical shading angles, VSA = 57°, slats width was calculated as described in Equation (3):

$$W=\frac{e}{tan\alpha sin\beta +cos\beta }$$

(3)

where:

• W: Slats width (m).
• α: Optimal lower vertical shading angle VSA = 57°.
• β: Tilted angle of the slats.
• e: Spacing between slats (m) = H/slats number.
• H: High of window (m) = 1.80.

In this research, the impact of three solar protection design parameters was analyzed:

• Vertical distance between slats “e”: H, H/2, H/4, H/8 and H/16;
• Slats tilted angles: 90° (horizontal), 60° and 120°; for this group of cases “e” was fixed to H/8. Additionally, installations of slats: vertical installation and horizontal installation with two tilted angles of slat (45° and 135°).

To differentiate the simulated cases we used an identification system which was an alphanumeric code A.XX.YY with (

Table 1. Geometrical configurations of external shading devices for simulation study.

	Reference Case	V.1.90	V.2.90	V.4.90	V.8.90
Installation	/	Vertical	Vertical	Vertical	Vertical
Slat spacing	/	H = 1.8 m	H/2 = 0.90 m	H/4 = 0.45	H/8 = 0.22 m
Tilted angle	/	90°	90°	90°	90°
Width (m)	/	1.2	0.6	0.3	0.15
	V.16.90	V.8.60	V.8.120	H.8.45	H.8.135
Installation	Vertical	Vertical	Vertical	Horizontal	Horizontal
Slat spacing	H/16 = 0.11 m	H/8 = 0.22 m	H/8 = 0.22 m	L/8 = 0.125 m	L/8 = 0.125 m
Tilted angle	90°	60°	120°	45°	135°
Width (m)	0.07	0.12	0.27	0.18	0.27

):

• A: Slats installation; V vertical, H horizontal.
• XX: Spacing between slats; 1-H, 2-H/2, 4-H/4, 8-H/8 and 16-H/16.
• YY: Tilted angle; 60–60°, 90–90°, 120–120°.

2.4. Simulation Tools and Conditions

2.4.1. Thermal Analysis

TRNSYS.17 simulation software was used to calculate air temperatures, solar gains and energy demand for cooling and heating for each external shading device. Thermal simulation was realized for the whole year. For air temperature, were the only results presented were for the coolest and the hottest months, respectively, January and July. Simulation results were compared with the reference case without shading.

Table 2. Simulation settings for the room model used in TRNSYS 17.

Climate and Geometry
Climatic data	Ghardaïa
Room area	24 m2
Room volume	72 m3
Time Settings
Time	January to December
Total operation hours	8760 h
Set-Point Temperature
Heating set-point	20 °C
Cooling set-point	26 °C
Wall
Thickness (cm)	30
Heat transfer coefficient (W/m2K)	0.962
Heat capacity (kJ/kg_K)	0.79
Density (kg/m3)	720
Surface area exposed to the outside (m2)	84
Roof
Thickness (cm)	20
Heat capacity (kJ/kg_K)	0.65
Density (kg/m3)	2500
Ground Roof
Thickness (cm)	20
Heat capacity (kJ/kg_K)	0.79
Density (kg/m3)	2500
Window
Window orientation	South
Window to wall ratio	30%
Length	2 m
Height	1.8 m
U value glass (W/m2K)	5.74
G value	87%

summarizes simulation settings.

2.4.2. Daylighting Analysis

The proposed geometrical configurations were evaluated using daylighting analysis simulation through two advanced software tools, Desktop Radiance 2.0 [32] and DAYSIM 3.1, which are effective in simulating daylighting performance [33].

In this research, the daylight analysis was carried out for two types of metrics for measuring daylighting:

• Static daylight metrics, measured at a single point in time, using RADIANCE 2.0 to calculate illuminance level and DAYSIM 3.1 to calculate Daylight Factor (DF).
• Additionally, annual dynamic daylighting metrics using DAYSIM 3.1 to calculate daylight autonomy (DA), spatial daylight autonomy (sDA_500lx,50%) and uniformity daylight factor (UDF).

Based on the BS 8206-2:2008 standards [34], the threshold lighting levels were 500 lx in a minimum of 75% of the plan area, and to minimize the glare issues, the minimum percentage of the plan area with natural light levels exceeding 3000 lux were searched [35].

Daylight Autonomy (DA) is a dynamic daylight metric proposed by the Association Suisse des Electriciens in 1989 and improved by Christoph Reinhart between 2001 and 2004 [36]. Daylight Autonomy (DA) is defined as the percentage of occupied time during the year when a minimum work plane illuminance threshold of 500 lx can be maintained by daylight alone [37], while spatial Daylight Autonomy (sDA) describes the percentage of area that is above 500 lx for 50% of the occupied hours [38]. According to LEED v4 [39], accepted sDA is 55% and preferred sDA is 75%.

Daylight Factor (DF) is a static indicator of daylight performance and the ratio of the internal horizontal illuminance at a point to the external horizontal illuminance under an overcast CIE sky [40]. According to BS 8206-2:2008 standards [34], for average daylight factor, a minimum value of 2% is required for workspaces in a minimum of 75% of the plan areas. However, uniformity daylight factor (UDF) expresses the degree of homogeneity in lighting distribution, defined as the ratio of the minimum DF to the average DF value of the entire plan (UDF = DF min/DF average). The threshold of 0.40 was fixed by the assessment method for sustainable buildings BREEAM 2.08 to achieve an efficient working environment [41].

The daylighting simulations were conducted during both winter and summer solstices (21 December and 21 June) and during the summer solstice at 08:00 h, 12:00 h and 16:00 h for measuring static daylight metrics using Desktop Radiance 2.0 and during the whole year for annual dynamic daylighting metrics using DAYSIM 3.1. Simulation settings are presented in

Table 3. Simulation settings for the room model used in RADIANCE 2.0 and DAYSIM 3.1.

Climate and Geometry
Sky and weather	CIE Clear
Location	Ghardaïa
Latitude	32.23° N
Longitude	3.49° E
Altitude	450 m
Turbidity	3
Room Dimensions
Area	24 m2
Volume	72 m3
Time Settings for RADIANCE 2.0
Time	21 June 21 December
Hours	8 h, 12 h, 16 h
Time Settings for DAYSIM 3.1
Time	Annual
Hours	8 h to 18 h
Surfaces Properties
Wall reflectance	60%
Floor reflectance	40%
Ceiling reflectance	80%
Window
Window orientation	South
Length	2 m
Height	1.8 m
Work plan level	0.8 m
Grid
Size	24 × 16
Spacing	0.25 m
Glass Properties
Type	Clear glass
Transmittance	86%
Reflectance	5%
Shading Devices Properties
Color	white
Size	See Table 1
Material	Aluminum
Solar reflectance	85%
Solar absorption	15%
Solar transmission	00%

.

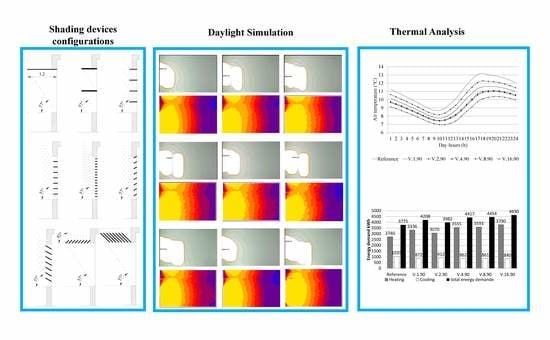
3. Results

3.1. Daylight Simulation

3.1.1. Spacing between Slats

Results presented in

Table 4. Daylight autonomy and illuminance calculated on 21 December and 21 June for cases with different spacing between slats.

Case		Illuminance		Daylight Autonomy DA500
		21 December—12h00	21 June—12h00
Reference case
		921 lx–29,420 lx	412 lx–23,565 lx		sDA500lx 50% = 80.92%
V.1.90
		572 lx–28,667 lx	366 lx–2140 lx		sDA500lx 50% = 57.62%
V.2.90
		663 lx–29,497 lx	373 lx–2331 lx		sDA500lx 50% = 63.12%
V.4.90
		663 lx–28,644 lx	370 lx–2597 lx		sDA500lx 50% = 65.17%
V.8.90
		637 lx–27,292 lx	357 lx–2283 lx		sDA500lx 50% = 66.62%
V.16.90
		615 lx–28,465 lx	356 lx–2191 lx		sDA500lx 50% = 67.21%

show that all cases decreased the maximum and minimum illuminance levels in both December and June compared to the base case.

In December, the “V.1.90” case recorded the lowest minimum illuminance (572 lx) that was reduced by up to 38% compared to the base case; however, the “V.2.90” and “V.4.90” cases recorded the highest values, and they reduced the minimum illuminance by up to 28%. For maximum illuminance, the impact was insignificant; the “V.2.90” case recorded almost the same value as the reference case, and the other cases reduced the maximum illuminance by only 3%. Even though all cases reduced the illuminance level in December compared to the base case, it was still up to the required task level (500lx) in a 100% of the plan area.

In June, the “V.8.90” and “V.16.90” cases recorded the lowest minimum illuminance, which was reduced by up to 13% compared to the base case. The “V.2.90” case recorded the highest value; it reduced the minimum illuminance by up to 9%. It is to be highlight that the minimum illuminance in all cases was below the target illuminance (500 lx) even for the base case. The use of shading devices with different spacing between slats had a significant impact on the maximum illuminance; thus, reducing illuminance by more than 89% and removing all risks associated with glare.

The analysis of DA₅₀₀ showed that, according to the reference case, no case improved the DA₅₀₀. Case V.1.90 produced the lowest value. It decreased sDA₅₀₀ by up to 28%; however, the “V.16.90” case produced the highest value of sDA₅₀₀. It was about 67.21%. However, it has to be highlighted that sDA₅₀₀ was above the acceptance value (55%) for all cases.

Regarding the reference case, the percentage of the plan area exceeding 2% DF was 79%, and although the uniformity daylight factor did not reach the threshold of 0.40 UDF, it was about 0.32. Even though all cases, with different spacing between slats, increased the uniformity daylight factor satisfying the threshold of 0.40 UDF except the “V.2.90” case, the percentage of the plan area exceeding 2% did not exceed 75% (

Table 5. Daylight factor (DF) and uniformity daylight factor (UDF) calculated for cases with different spacing between slats. The values satisfying the international lighting standards are in bold.

Case	Minimum DF	Maximum DF	Average DF	DF > 2 %	Uniformity Daylight Factor DF min/DF Average
Reference case	1.43	25.13	4.44	79	0.32
V.1.90	1.33	15.2	3	59.17	0.44
V.2.90	1.29	20.76	3.51	65.42	0.37
V.4.90	1.29	11.8	3.26	70.21	0.40
V.8.90	1.35	9.19	2.98	67.25	0.45
V.16.90	1.42	9.84	3.01	68.88	0.47

. Daylight factor (DF) and uniformity daylight factor (UDF) calculated for cases with different spacing between slats).

3.1.2. Tilted Angle of the Slats

Simulation results in

Table 6. Daylight autonomy and illuminance calculated on 21 December and 21 June for cases with different tilted angle of slats.

Case		Illuminance		Daylight Autonomy DA500
		21 December—12h00	21 June—12h00
Reference case
		921 lx–29,420 lx	412 lx–23,565 lx		sDA500lx 50% = 80.92%
V.8.90
		637 lx–27,292 lx	357 lx–2283 lx		sDA500lx 50% = 66.62%
V.8.60
		534 lx–27,084 lx	350 lx–1938 lx		sDA500lx 50% = 58.46%
V.8.120
		668 lx–28,578 lx	256 lx–1665 lx		sDA500lx 50% = 62.33%

show that the use of shading devices with different tilted angles, i.e., 60°, 90 and 120°, decreased the minimum and maximum illuminance levels compared to the reference case.

In December, the case “V.8.120” recorded the highest minimum and maximum illuminance, which were reduced by up to 27% and 3%, respectively, compared to the base case. The lowest maximum and minimum illuminance were recorded for case “V.8.60”, and they were reduced by up to 42% and 8%, respectively, compared to the base case. The case “V.8.90” reduced the minimum illuminance by up to 30% and the maximum illuminance by up to 7%. It has to be highlighted that, in December, the illuminance was still up to the required task level (500 lx) in 100% of the plan area for all cases.

In June, contrary to December, case “V.8.120” recorded the lowest minimum and maximum illuminance, which were reduced by up to 38% and 92%, respectively. The case “V.8.90” recorded the highest minimum and maximum illuminance, which was reduced by up to 13% and 90%, respectively, compared to the base case. Case “V.8.60” reduced the minimum and maximum illuminance by up to 15% and 91%, respectively. It is to highlight that all cases removed any risk associated with glare in June.

All cases with a different tilted angle decreased sDA in the space. The case “V.8.90” recorded the highest value of sDA—it was about 66.62%—followed by V.8.120 which recorded an sDA of 62.33%. However, case V.8.60 recorded the lowest value of about 58.46 %. Even though all cases reduced the sDA compared to the base case, it was still above the acceptance value (55%).

Results for the Uniformity Daylight Factor (UDF) (

Table 7. Daylight factor (DF) and uniformity daylight factor (UDF) calculated for cases with different tilted angle of slats. The values satisfying the international lighting standards are in bold.

Case	Minimum DF	Maximum DF	Average DF	DF > 2 %	Uniformity Daylight Factor DF min/DF Average
Reference case	1.43	25.13	4.44	79	0.32
V.8.90	1.35	9.19	2.98	67.25	0.45
V.8.60	1.35	7.31	2.59	57.00	0.52
V.8.120	1.32	11.4	3.3	67.12	0.40

) show that all cases, with different tilted angles, improved the uniformity daylight factor, satisfying the threshold of 0.40 UDF; we recorded 0.45, 0.52 and 0.4 corresponding to “V.8.60”, “V.8.120” and “V.8.90”, respectively. Nevertheless, the percentage of the plan area above 2% did not exceed 75%. It was 67.25%, 57% and 67.12% corresponding to “V.8.90”, “V.8.60” and “V.8.120”, respectively.

3.1.3. Slats Installation

Simulation results presented in

Table 8. Daylight autonomy and illuminance calculated on 21 December and 21 June for case with different slat installation.

Case		Illuminance		Daylight Autonomy DA500
		21 December—12h00	21 June 21st—12h00
V.8.90
		637 lx–27,292 lx	357 lx–2283 lx		sDA500lx 50% = 66.62%
H.8.45
		587 lx–28,950 lx	373 lx–2649 lx		sDA500lx 50% = 58.50%
H.8.135
		706 lx–28,930 lx	358 Lx–2239 lx		sDA500lx 50% = 62.33%

show that both horizontal and vertical installation of slats decreased the maximum and minimum illuminance levels compared to the reference case. In December, case “H.8.135” recorded the highest minimum illuminance; it was about 709 lx and reduced by up to 23%. Case “V.8.90” reduced the minimum illuminance by up to 31% and case “H.8.45” reduced the minimum illuminance by up to 36%, recording the lowest value. The two cases “H.8.135” and “H.8.45”, i.e., with a horizontal installation of slats, recorded the highest maximum illuminance that was almost equal to the value recorded by the reference case. Case “V.8.90” reduced the maximum illuminance by up to 7%. We note that, in December, the illuminance was still up to the required task level (500lx) for the three cases. In June, cases “V.8.90” and “H.8.135” almost recorded the same maximum and minimum illuminance. They reduced the minimum illuminance by 13% and the maximum illuminance by 90%. Case “H.8.45” recorded the highest minimum and maximum illuminance, which were reduced by 9% and 88%, respectively. In June, the maximum illuminance recorded by the three cases did not exceed 3000 lx in 100% of the plan area, which minimized the glare issues. However, the percentage of the plan area exceeding 500 lx was below the threshold of 75.0% of the plan.

The analysis of DA₅₀₀ shows that, according to the reference case, the use of shading devices with different installation caused a noticeable reduction in DA. Case “H.8.45” produced the lowest sDA₅₀₀ of about 58.50%, which was reduced by 28%; however, case “V.8.90” produced the highest value of sDA₅₀₀—it was about 66.62%—while case “H.8.135” recorded an sDA₅₀₀ of about 62.33%. It has to be highlighted that sDA₅₀₀ was above the acceptance value (55%) for all cases.

Simulation results presented in

Table 9. Daylight factor (DF) and uniformity daylight factor (UDF) calculated for cases with different installation. The values satisfying the international lighting standards are in bold.

Case	Minimum DF	Maximum DF	Average DF	DF > 2 %	Uniformity Daylight Factor DF min/DF Average
V.8.90	1.35	9.19	2.98	67.25	0.45
H.8.45	1.22	20.47	3.44	56.38	0.35
H.8.135	1.21	16.02	3.12	57.00	0.39

indicate that, for the two cases with a horizontal installation, i.e., cases “H.8.45” and “H.8.135”, the Uniformity Daylight Factor did not reach the threshold of 0.40 UDF—it was about 0.35 and 0.39, respectively. The percentage of the plan area exceeding 2% DF was also below the threshold of 75%. However, the case with a vertical installation, i.e., “V.8.90”, improved the UDF that was about 0.45, but the percentage of the plan area exceeding 2% DF was about 67% and remained below the threshold of 75%.

3.2. Thermal Analysis

This section presents and discusses the results of thermal analysis, i.e., the air temperature and energy demand for cooling and heating. The results allowed for a comparative evaluation of the different geometrical configurations of shading devices under study.

3.2.1. Air Temperature

We present and discuss, in this section, the results in terms of indoor air temperature calculated for a different geometrical configuration of shading devices compared to the reference case. We present the result for January and July corresponding, respectively, to the coolest and the hottest month.

Spacing between Slats

We measured and compared the air temperature in cases with different spacing with the reference case, i.e., without shading devices. Figure 6 shows air temperatures in January and July. We note that using shading devices reduced the interior temperature compared to the reference case.

• In January, in the afternoon the air temperature was reduced by up to 1 °C for the “V.2.90” case, 1.8 °C for the “V.1.90” case, 2.3 °C for both cases “V.4.90” and “V.8.90” and 3 °C for the “V.16.90” case. In the morning, the difference was less important; it was about 0.5 °C for case “V.2.90”, 0.9 °C for case “V.1.90”, 0.3 °C for both cases “V.4.90” and “V.8.90” and 1.7 °C for case “V.16.90”.
• However, in July, the difference of air temperature did not exceed 0.6 °C for all cases. Cases with different spacing between slats presented a similar behavior; they reduced the air temperature by approximately the same rate.

Tilted Angle of the Slats

Simulation results presented in Figure 7 show the air temperature within the space, allowing the comparative evaluation of the effect of the slats tilted angle.

• In January, the use of shading devices considerably reduced the indoor air temperature according to the reference case; we recorded a difference of 2.8 °C, 2.3 °C and 1.2 °C for cases “V.8.60”, “V.8.90” and “V.8.120”, respectively.
• However, the three cases presented almost the same air temperatures in July, with a difference of 0.5 °C compared to the reference case.

Slats Installation

Simulation results presented in Figure 8 show that:

• In January, in the afternoon the air temperature was reduced by up to 1.7 °C for case “H.8.135” and 2.5 °C for both cases “H.8.45” and “V.8.90”. In the morning, these differences were less important; they were about 1 °C for case “H.8.135” and 1.5 °C for cases “H.8.45” and V.8.90”.
• In July, the three cases presented a similar behavior, and the difference in air temperature did not exceed 0.4 °C.

3.2.2. Cooling and Heating Energy Demand

This section presents and discusses the results of heating, cooling and the total annual energy demand calculated for the different geometrical configuration of shading devices. For comparative evaluation purposes, bar charts also show the energy demand calculated for the reference case.

Vertical Distance between Slats

Heating, cooling and the total annual energy demand resulting from the use of different spacing between slats in comparison with the base case are summarized in Figure 9. Results show that:

• The cooling energy saving results for cases “V.1.90”, “V.2.90”, “V.4.90”, “V.8.90” and “V.16.90” reached 16%, 12%, 17%, 17% and 19%, respectively. However, the use of shading devices with different slat spacing produced a negative effect on the heating energy demand, where energy saving was negative in all cases.
• The energy use for heating, compared to the reference case, increased by 21%, 12%, 29%, 31% and 38% for cases “V.1.90”, “V.2.90”, “V.4.90” and “V.8.90”, respectively.
• The total energy demand increased for all cases compared to the reference case, i.e., without shading devices. Case “V.2.90” presented the lowest value; it increased the total energy demand by only 5.5%. However, case “V.16.90” recorded the highest value; it increased the total energy demand by 22.6%. Cases “V.1.90”, “V.4.90” and “V.8.90” were, respectively, up by 11.5%, 17% and 18%.

Tilted Angle of the Slats

Simulation results presented in Figure 10 show that the shading devices with different tilted angles, i.e., 60°, 90 and 120°, recorded almost the same cooling energy demand.

• The cooling energy saving was about 17% compared to the reference case. However, the use of shading devices with different tilted angles increased the heating energy demand that was reduced by 36%, 31% and 21% corresponding to cases “V.8.60”, “V.8.90” and “V.8.120”, respectively.
• We note that the heating energy demand increased by reducing the slat tilted angle. This was mainly due to the direct solar radiation that decreased by the reducing slat tilted angle.
• The total energy demand also increased by using shading devices with different tilted angles; we recorded an increase of about 10,5%, 18% and 21% corresponding to cases “V.8.120”, “V.8.90” and “V.8.60”, respectively.

Slats Installation

Simulation results presented in Figure 11 show that:

• All cases decreased the cooling energy demand compared to the reference case. We note that the two cases with a horizontal installation, i.e., cases “H.8.45” and “H.8.135”, recorded a cooling energy demand less than the case with a vertical installation, although the difference between the three cases was insignificant, since the energy saving was about 17% compared to the reference case.
• Nevertheless, the three cases increased the heating energy demand. The “H.8.135” case presented the lowest value that was increased by 26% compared to the reference case. Cases “V.8.90” and “H.8.45” increased the heating energy demand by 31% and 32% similarly.
• The total energy demand increased in all cases; case “H.8.135” recorded the lowest value that was up by 14% compared to the reference case. The other two cases almost recorded the same total energy demand. The increase was about 18% for case “V.8.90” and 19% for case “H.8.45”.

4. Discussion

The analysis of the simulation results allowed for the comparative evaluation of external shading devices, indicating the appropriate geometrical configurations for the improvement of daylight and thermal performances.

In this section, we discuss the relationship between the shading device performance and design parameters. We note that, in spite of the fact that the vertical shading angle (VSA) calculated for the overheating period was fixed, cases under study did not have the same thermal and luminous behavior. This might be explained by indicators depending on design parameters (spacing between slat, slat tilted angle and installation). Those indicators are:

• The amount of direct solar radiation: it is the ratio between the sunny window area and the window area (Figure 12)
• Shading coefficient: it is the ratio between the shading window area and the window area. It is equal to 100- Direct solar radiation (Figure 13)
• Reflected radiation from slats: it is the ratio between the amount of solar radiation reflected by slats arriving to the window (m²) and the window area (Figure 14)
• Reflected radiation from soil: it is the ratio between the amount of solar radiation reflected by soil arriving to the window (m²) and the window area (Figure 15)
• Penetration of solar radiation, defined by the ratio of distance, measured from the facade, reached by the direct solar radiation to the space depth (Figure 16). And the visual permeability that depends only on shading devices configuration i.e., spacing between slats, slat tilted angle and slat installation. It is the ratio between projected open area and window area. In other words, visual permeability is the difference between the window area and the projected shaded area (Figure 17).

The first five indicators depended on the solar position as well as the design parameters. However, the last one, i.e., the visual permeability, depended only on the design parameters and did not change by changing the solar position. These indicators were graphically presented, for each case, and measured for different geometrical configurations in December and June.

We note that the sDA, air temperature, heating and total energy demand increased by decreasing the spacing between slats, while the cooling energy demand and illuminance decreased. This was due to the fact that, in December, the direct solar radiation and reflected radiation from soil (Figure 12 and Figure 15) reduced by decreasing the spacing between slats; however, the shading coefficient increased (Figure 13).

The uniformity daylight factor (UDF) increased by decreasing the spacing between slats; this may be explained by the fact that the penetration of the solar radiation and reflected radiation from slats increased (Figure 15 and Figure 16).

In December, the maximum and minimum illuminance decreased by reducing the slat tilted angle; this was mainly due to the amount of the direct solar radiation and solar penetration, which reduced by reducing the slat tilted angle (Figure 12 and Figure 16). However, in June the maximum and minimum illuminance were not in correlation with the tilted angle, since the direct solar radiation and solar penetration were zero in June for cases with a different tilted angle (Figure 12 and Figure 16), but depending on the visual permeability which was the highest in the case with horizontal slats (Figure 17). We note that the heating and total energy demand reduced by decreasing the tilted angle of slats. However, the cooling energy demand depended on the visual permeability.

The uniformity daylight factor (UDF) increased by decreasing the tilted angle of slats, this may be explained by the fact that the direct solar radiation and penetration increased (Figure 12 and Figure 16). We note here that, according to [10,20], the total annual energy consumption and lighting level changed in correlation with the tilted angle of slats. In these studies, the slat width was fixed which means that the VSA changed by changing the tilted angle; however, in our research, the slat width changed by changing the tilted angle in order to have the same VSA, so there was no correlation in the overheating period; this was mainly due to the shading coefficient that was 100% for all cases (Figure 13).

The two cases with a horizontal installation, i.e., cases H.8.45 and H.8.135, reduced sDA compared to cases with a vertical installation and slat angle of 90°, except for case V.1.90, i.e., the overhang. We note that case H.8.135 recorded the same sDA as case V.8.120, while case H.8.45 recorded the same sDA as case V.8.120. This may be explained by the fact that each two similar cases had the same amount of direct solar radiation and penetration (Figure 12 and Figure 16).

We note that the sDA and air temperature in December and the heating energy demand were more important when the tilted angle was 135°, i.e., greater than 90°. However, the cooling and total energy demand were less important. This may be explained by the fact that this case allowed for the penetration of direct solar radiation between slats when the solar altitude was lower than VSA, i.e., in winter, contrary to cases when the tilted angle was less than 90° (Figure 16).

Reducing the spacing between slats and the tilted angle improved the uniformity and, thus, minimized the glare issues. However, cases with a horizontal installation had a low daylight uniformity, which increased the possibilities of glare issues.

Generally, in June the changing parameter values had an insignificant impact, particularly on the air temperature and cooling energy demand. This was mainly due to the vertical shading angle that was calculated to have a 100% shading coefficient in the overheating period; thus, eliminating the direct solar radiation (Figure 12 and Figure 13)

5. Conclusions

In this paper, we evaluated, through simulations, the external shading devices performance in a hot climate. More specifically, we analyzed the effect of three design parameters: the spacing between slats, tilted angle of slats and their installation. Our objective was to define parameters affecting the external shading devices’ behavior, and study their impact on the energy demand, daylighting and thermal conditions within spaces. We used three software: RADIANCE 2.0 and DAYSIM 3.1 for the daylighting simulation and TRNSYS.17 for the thermal dynamic simulation.

The analysis of the simulation results, based on a comparative evaluation of the different external shading devices under study, allowed for indicating the appropriate geometrical configurations able to reduce the energy demand and to improve the luminous and thermal conditions.

The daylight simulation analysis showed that all the geometrical configurations of shading devices under study reduced the maximum and minimum illuminance in both December and June compared to the base case, i.e., without shading devices. In December, the illuminance was still up to the required level (500 lx) in 100% of the plan area. In June, the percentage of the plan area exceeding 500 lx was less of 75%. On the other hand, the illuminance recorded in June for all cases did not exceed 3000 lx in 100% of the plan area and, thus, removed all risks associated with glare; whereas, in December, shading devices were not able to mitigate the glare when the solar altitude was low and, thereby, the direct solar radiation was increased.

Regarding the daylight autonomy (DA), the analysis showed that all cases reduced sDA₅₀₀, but it was above the acceptance value (55%) for all cases. In most cases, the uniformity daylight factor exceeded the threshold of 0.40 UDF, satisfying the international lighting standards; however, the percentage of the plan area exceeding 2% DF was above 75% for all cases.

The thermal simulation analysis showed that the use of shading devices reduced the air temperature in both January and July. Their impact was more important in January, where the difference of air temperature was up to 3 °C compared to the reference case; however, this difference did not exceed 0.6 °C in July.

The simulations showed that external shading devices were effective in reducing building cooling loads in summer, providing up to 19% energy savings. However, the energy demand for heating and the total annual energy demand increased significantly; the difference was up by 38% and 22%, respectively.

We note that, in spite of the fact that the vertical shading angle (VSA) calculated for the overheating period was fixed for all cases, the differences between the geometrical configurations under study were recorded. The difference between cases was mainly due to the amount of direct and indirect solar radiation entering space, i.e., the direct solar radiation, shading coefficient, reflected radiation from slats and soil, and penetration, which was the percentage of the plan area reached by the solar radiation. Another parameter that did not depend on the solar position was the visual permeability that depended only on the shading devices configuration, i.e., spacing between slats, slat tilted angle and slat installation.

Finally, it has to be highlighted that no case was able to improve both the thermal and daylight performance; cases recording the highest illuminance and sDA, the highest air temperature in winter and the lowest heating energy demand recorded the highest air temperature in summer and the highest cooling energy demand, and the opposite too. Therefore, the choice of the appropriate shading devices configuration should be based on a multi-criteria analysis.

This study only focused on the flat slats for the south-oriented facade in a hot dry climate. Future research should investigate the impact of slats’ shape and shading materials for different orientations as well as for different climatic conditions. In addition, we must give importance to the dynamic solar shading, the combination of internal and external shading and the integration of photovoltaic cells on the slats that contributed positively to the overall energy balance of the building by increasing the solar energy production.