Modelling and Forecasting Temporal PM2.5 Concentration Using Ensemble Machine Learning Methods
Abstract
:1. Introduction
Significance of PM2.5
2. Methods
2.1. Study Area and Data
2.2. Modeling Techniques
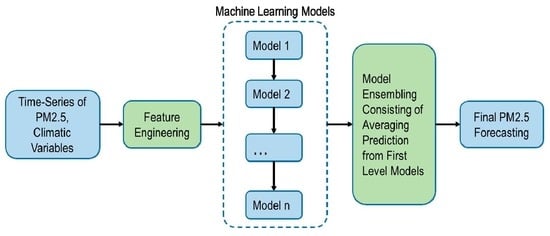
2.3. Modeling Process
2.4. Forecast Accuracy
3. Results
3.1. Exploratory Data Analysis
3.2. Univariate Models
3.3. Multivariate Models
3.4. Ensemble Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations. 68% of the World Population Projected to Live in Urban Areas by 2050, Says UN. Available online: https://www.un.org/development/desa/en/news/population/2018-revision-of-world-urbanization-prospects.html (accessed on 10 April 2021).
- Okunlola, P. The Power and the Heartbeat of West Africa’s Biggest Urban Jungle; UN-HABITAT: Nairobi, Kenya, 2010. [Google Scholar]
- Arshad, M.; Khedher, K.M.; Eid, E.M.; Aina, Y.A. Evaluation of the urban heat island over Abha-Khamis Mushait tourist resort due to rapid urbanisation in Asir, Saudi Arabia. Urban Clim. 2021, 36, 100772. [Google Scholar] [CrossRef]
- Rodríguez, M.C.; Dupont-Courtade, L.; Oueslati, W. Air pollution and urban structure linkages: Evidence from European cities. Renew. Sustain. Energy Rev. 2016, 53, 1–9. [Google Scholar] [CrossRef]
- Birnbaum, H.G.; Carley, C.D.; Desai, U.; Ou, S.; Zuckerman, P.R. Measuring the Impact of Air Pollution on Health Care Costs: Study examines the impact of air pollution on health care costs. Health Aff. 2020, 39, 2113–2119. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Park, T.-W.; Deng, Y. Quantifying the relationship between extreme air pollution events and extreme weather events. Atmos. Res. 2017, 188, 64–79. [Google Scholar] [CrossRef]
- Drye, E.E.; Özkaynak, H.; Burbank, B.; Billick, I.H.; Spengler, J.D.; Ryan, P.B.; Baker, P.E.; Colome, S.D. Development of Models for Predicting the Distribution of Indoor Nitrogen Dioxide Concentrations. JAPCA 1989, 39, 1169–1177. [Google Scholar] [CrossRef] [Green Version]
- Feng, X.; Li, Q.; Zhu, Y.; Hou, J.; Jin, L.; Wang, J. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation. Atmos. Environ. 2015, 107, 118–128. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, Y.; Vanos, J.K.; Cao, G. Day-of-week and seasonal patterns of PM2.5 concentrations over the United States: Time-series analyses using the Prophet procedure. Atmos. Environ. 2018, 192, 116–127. [Google Scholar] [CrossRef]
- Zhou, Y.; Chang, F.-J.; Chang, L.-C.; Kao, I.-F.; Wang, Y.-S.; Kang, C.-C. Multi-output support vector machine for regional multi-step-ahead PM2.5 forecasting. Sci. Total Environ. 2019, 651, 230–240. [Google Scholar] [CrossRef]
- Oshodi, O.; Edwards, D.J.; Lam, K.C.; Olanipekun, A.O.; Aigbavboa, C.O. Construction output modelling: A systematic review. Eng. Constr. Arch. Manag. 2020, 27, 2959–2991. [Google Scholar] [CrossRef]
- McKendry, I.G. Evaluation of Artificial Neural Networks for Fine Particulate Pollution (PM10 and PM2.5) Forecasting. J. Air Waste Manag. Assoc. 2002, 52, 1096–1101. [Google Scholar] [CrossRef] [Green Version]
- Rocha, M.; Cortez, P.; Neves, J. Evolution of neural networks for classification and regression. Neurocomputing 2007, 70, 2809–2816. [Google Scholar] [CrossRef] [Green Version]
- Luo, S.-T.; Cheng, B.-W. Diagnosing Breast Masses in Digital Mammography Using Feature Selection and Ensemble Methods. J. Med. Syst. 2010, 36, 569–577. [Google Scholar] [CrossRef]
- Shishegaran, A.; Saeedi, M.; Kumar, A.; Ghiasinejad, H. Prediction of air quality in Tehran by developing the nonlinear ensemble model. J. Clean. Prod. 2020, 259, 120825. [Google Scholar] [CrossRef]
- Franceschi, F.; Cobo, M.; Figueredo, M. Discovering relationships and forecasting PM10 and PM2.5 concentrations in Bogotá, Colombia, using Artificial Neural Networks, Principal Component Analysis, and k-means clustering. Atmos. Pollut. Res. 2018, 9, 912–922. [Google Scholar] [CrossRef]
- Lu, F.; Xu, D.; Cheng, Y.; Dong, S.; Guo, C.; Jiang, X.; Zheng, X. Systematic review and meta-analysis of the adverse health effects of ambient PM2.5 and PM10 pollution in the Chinese population. Environ. Res. 2015, 136, 196–204. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Li, S.; Fan, C.; Bai, Z.; Yang, K. The impact of PM2.5 on asthma emergency department visits: A systematic review and meta-analysis. Environ. Sci. Pollut. Res. 2016, 23, 843–850. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, R.W.; Kang, S.; Anderson, H.R.; Mills, I.C.; Walton, H. Epidemiological time series studies of PM2.5and daily mortality and hospital admissions: A systematic review and meta-analysis. Thorax 2014, 69, 660–665. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lagos State Ministry of Economic Planning and Budget. Lagos State Development Plan 2012–2025. 2013. Available online: https://www.proshareng.com/admin/upload/report/11627-271150413-proshare.pdf (accessed on 13 November 2021).
- Oluseyi, T.; Akinyemi, M. Monitoring of concentration of air pollutants from vehicular emission along major highways and bypass within Kosofe Local Government Area, Lagos State. Unilag J. Med. Sci. Technol. 2017, 5, 104–115. [Google Scholar]
- Adenikinju, A.F. Electric infrastructure failures in Nigeria: A survey-based analysis of the costs and adjustment responses. Energy Policy 2003, 31, 1519–1530. [Google Scholar] [CrossRef]
- Zeng, L.; Offor, F.; Zhan, L.; Lyu, X.; Liang, Z.; Zhang, L.; Wang, J.; Cheng, H.; Guo, H. Comparison of PM2.5 pollution between an African city and an Asian metropolis. Sci. Total Environ. 2019, 696, 134069. [Google Scholar] [CrossRef]
- Liao, K.; Huang, X.; Dang, H.; Ren, Y.; Zuo, S.; Duan, C. Statistical Approaches for Forecasting Primary Air Pollutants: A Review. Atmosphere 2021, 12, 686. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 3rd ed.; OTexts: Melbourne, Australia, 2021. [Google Scholar]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The forecast Package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Brown, R.G. Statistical Forecasting for Inventory Control; McGraw/Hill: New York, NY, USA, 1959. [Google Scholar]
- Holt, C.C. Forecasting Seasonals and Trends by Exponentially Weighted Averages (ONR Memorandum No. 52); Carnegie Institute of Technology: Pittsburgh, OR, USA, 1957. [Google Scholar]
- Winters, P.R. Forecasting Sales by Exponentially Weighted Moving Averages. Manag. Sci. 1960, 6, 324–342. [Google Scholar] [CrossRef]
- Araz, O.M.; Bentley, D.; Muelleman, R.L. Using Google Flu Trends data in forecasting influenza-like–illness related ED visits in Omaha, Nebraska. Am. J. Emerg. Med. 2014, 32, 1016–1023. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Wu, X.; Gong, Y.; Yu, W.; Zhong, X. Holt–Winters smoothing enhanced by fruit fly optimization algorithm to forecast monthly electricity consumption. Energy 2020, 193, 116779. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Aguilera, H.; Guardiola-Albert, C.; Naranjo-Fernández, N.; Kohfahl, C. Towards flexible groundwater-level prediction for adaptive water management: Using Facebook’s Prophet forecasting approach. Hydrol. Sci. J. 2019, 64, 1504–1518. [Google Scholar] [CrossRef]
- Tadjer, A.; Hong, A.; Bratvold, R.B. Machine learning based decline curve analysis for short-term oil production forecast. Energy Explor. Exploit. 2021, 39, 1747–1769. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Cekim, H.O. Forecasting PM 10 concentrations using time series models: A case of the most polluted cities in Turkey. Environ. Sci. Pollut. Res. 2020, 27, 25612–25624. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Dancho, M. Working with the Time Series Index Using Timetk. 2017. Available online: https://mran.microsoft.com/snapshot/2017-12-11/web/packages/timetk/vignettes/TK01_Working_With_Time_Series_Index.html#tk_get_timeseries_signature-and-tk_augment_timeseries_signature (accessed on 14 August 2021).
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.D.A.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the Tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Kuhn, M.; Wickham, H. Tidymodels: A Collection of Packages for Modeling and Machine Learning Using Tidyverse Principles. 2020. Available online: https://www.tidymodels.org/ (accessed on 13 November 2021).
- Ben Taieb, S.; Bontempi, G.; Atiya, A.F.; Sorjamaa, A. A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition. Expert Syst. Appl. 2012, 39, 7067–7083. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Li, Z. Hourly PM2.5 concentration forecasting based on feature extraction and stacking-driven ensemble model for the winter of the Beijing-Tianjin-Hebei area. Atmos. Pollut. Res. 2020, 11, 110–121. [Google Scholar] [CrossRef]
- Tsai, C.-L.; Chen, W.T.; Chang, C.-S. Polynomial-Fourier series model for analyzing and predicting electricity consumption in buildings. Energy Build. 2016, 127, 301–312. [Google Scholar] [CrossRef]
- Hyndman, R.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef] [Green Version]
- Zhai, B.; Chen, J. Development of a stacked ensemble model for forecasting and analyzing daily average PM2.5 concentrations in Beijing, China. Sci. Total Environ. 2018, 635, 644–658. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Giuliano, G.; Habre, R. Estimating hourly PM2.5 concentrations at the neighborhood scale using a low-cost air sensor network: A Los Angeles case study. Environ. Res. 2021, 195, 110653. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Jiang, H.; Wang, J.; Zhou, J. A hybrid model for PM 2.5 forecasting based on ensemble empirical mode decomposition and a general regression neural network. Sci. Total Environ. 2014, 496, 264–274. [Google Scholar] [CrossRef]
- Wang, P.; Guo, H.; Hu, J.; Kota, S.H.; Ying, Q.; Zhang, H. Responses of PM2.5 and O3 concentrations to changes of meteorology and emissions in China. Sci. Total Environ. 2019, 662, 297–306. [Google Scholar] [CrossRef]
- Zhang, B. Real-time inflation forecast combination for time-varying coefficient models. J. Forecast. 2019, 38, 175–191. [Google Scholar] [CrossRef]
- Medeiros, M.C.; Vasconcelos, G.F.; Veiga, Á.; Zilberman, E. Forecasting inflation in a data-rich environment: The benefits of machine learning methods. J. Bus. Econ. Stat. 2021, 39, 98–119. [Google Scholar] [CrossRef]






| Variable | Unit | Before Data Cleaning | After Data Cleaning | ||||
|---|---|---|---|---|---|---|---|
| Range | Mean | SD | Range | Mean | SD | ||
| PM2.5 | µg/m3 | (1.73, 165.3) | 22.4 | 11.9 | (3.39, 65.96) | 21.9 | 9.8 |
| RH | (13.1, 90.7) | 66.7 | 14.3 | (14.65, 89.4) | 66.7 | 14.2 | |
| Temp | °C | (23.0, 43.0) | 32.2 | 4.2 | (24, 42.4) | 32.2 | 4.1 |
| S/N | Model | MAE | MASE | RMSE |
|---|---|---|---|---|
| 1 | ARIMA | 1.82 | 0.83 | 2.3518 |
| 2 | Prophet | 1.96 | 0.89 | 2.4895 |
| 3 | Exponential smoothing | 2.08 | 0.95 | 2.4839 |
| 4 | NNAR | 2.29 | 1.04 | 2.7129 |
| Name | Type | Description |
|---|---|---|
| Index.num | Numeric | Time is converted into seconds (Base = 1970-01-01 00:00:00) |
| Month | Categorical (01–12) | Month of each air quality measurement (e.g., December = 12) |
| Month.lbl | Dummy | Month of the year for each air quality measurement |
| Day | Categorical | Day of each air quality measurement (13 December 2020 = 13) |
| Hour | Categorical (0–23) | Hour of each air quality measurement |
| Hour12 | Categorical (0–11) | Hour of the day on a 12 h scale |
| am.pm | Categorical (1–2) | Morning = 1 and Afternoon = 2 |
| Wday | Categorical (1–7) | Day of the week (Sunday = 1, Monday = 2, …, Saturday = 7) |
| Wday.lbl | Dummy | Day of the week |
| Qday | Categorical | Day of the quarter |
| Yday | Categorical (1–365) | Day of the year |
| Mweek | Categorical | Week of the month |
| Week | Categorical | Week number of the year |
| Week2 | Categorical | The modulus for biweekly frequency |
| Week3 | Categorical | The modulus for triweekly frequency. |
| Week4 | Categorical | The modulus for quadweekly frequency |
| Mday7 | Categorical (1, 2, …, 5) | The integer division of day of the month by seven (e.g., the first Saturday of the month has mday7 = 1 |
| S/N | Input Variables | Description of Models |
|---|---|---|
| 1 | Calendar-related features | Prophet_time, XGBoost_time, SVM_time, NN_time, RF_time |
| 2 | 24th Lag of PM2.5, and 24 h, 48 h, and 72 h moving averages of PM2.5 + calendar-related features | Prophet_lag, XGBoost_lag, SVM_lag, NN_lag, RF_lag |
| 3 | Relative humidity + calendar-related features + lag features | Prophet_RH, XGBoost_RH, SVM_RH, NN_RH, RF_RH |
| 4 | Temperature + calendar-related features + lag features | Prophet_Temp, XGBoost_Temp, SVM_Temp, NN_Temp, RF_Temp |
| 5 | Relative humidity + temperature + calendar-related features + lag features | Prophet_All, XGBoost_All, SVM_All, NN_All, RF_All |
| Model_id | Model Description | MAE | MASE | RMSE |
|---|---|---|---|---|
| 1 | XGBoost_All | 1.69 | 0.77 | 2.3809 |
| 2 | RF_All | 1.81 | 0.82 | 2.3730 |
| 3 | RF_Temp | 1.82 | 0.83 | 2.3582 |
| 4 | RF_RH | 1.83 | 0.83 | 2.4226 |
| 5 | RF_Lag | 2.02 | 0.92 | 2.4825 |
| 6 | XGBoost_Lag | 2.02 | 0.92 | 2.5920 |
| 7 | XGBoost_Temp | 2.10 | 0.96 | 2.5971 |
| 8 | Prophet_Temp | 2.16 | 0.98 | 2.6942 |
| 9 | RF_Time | 2.26 | 1.03 | 2.7664 |
| 10 | Prophet_Time | 2.30 | 1.04 | 2.9765 |
| 11 | NN_Lag | 2.31 | 1.05 | 2.7369 |
| 12 | Prophet_All | 2.34 | 1.06 | 2.8370 |
| 13 | SVM_Lag | 2.35 | 1.07 | 3.0027 |
| 14 | SVM_Temp | 2.45 | 1.11 | 3.1188 |
| 15 | Prophet_RH | 2.64 | 1.20 | 3.2143 |
| 16 | Prophet_Lag | 2.65 | 1.21 | 3.2254 |
| 17 | SVM_Time | 2.66 | 1.21 | 3.26243 |
| 18 | XGBoost_RH | 2.90 | 1.32 | 3.7129 |
| 19 | SVM_RH | 2.95 | 1.34 | 3.5400 |
| 20 | SVM_All | 2.95 | 1.34 | 3.5315 |
| 21 | NN_RH | 3.35 | 1.52 | 4.6193 |
| 22 | NN_All | 3.73 | 1.70 | 4.3048 |
| 23 | XGBoost_Time | 5.19 | 2.36 | 6.0694 |
| 24 | NN_Temp | 6.07 | 2.76 | 6.6457 |
| 25 | NN_Time | 7.53 | 3.42 | 8.0063 |
| S/N | Model | MAE | MASE | RMSE |
|---|---|---|---|---|
| 1 | Ensemble (weighted) | 1.57 | 0.71 | 2.1876 |
| 2 | Ensemble (mean) | 1.60 | 0.73 | 2.1985 |
| 3 | Ensemble (median) | 1.61 | 0.73 | 2.1830 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ejohwomu, O.A.; Shamsideen Oshodi, O.; Oladokun, M.; Bukoye, O.T.; Emekwuru, N.; Sotunbo, A.; Adenuga, O. Modelling and Forecasting Temporal PM2.5 Concentration Using Ensemble Machine Learning Methods. Buildings 2022, 12, 46. https://doi.org/10.3390/buildings12010046
Ejohwomu OA, Shamsideen Oshodi O, Oladokun M, Bukoye OT, Emekwuru N, Sotunbo A, Adenuga O. Modelling and Forecasting Temporal PM2.5 Concentration Using Ensemble Machine Learning Methods. Buildings. 2022; 12(1):46. https://doi.org/10.3390/buildings12010046
Chicago/Turabian StyleEjohwomu, Obuks Augustine, Olakekan Shamsideen Oshodi, Majeed Oladokun, Oyegoke Teslim Bukoye, Nwabueze Emekwuru, Adegboyega Sotunbo, and Olumide Adenuga. 2022. "Modelling and Forecasting Temporal PM2.5 Concentration Using Ensemble Machine Learning Methods" Buildings 12, no. 1: 46. https://doi.org/10.3390/buildings12010046
APA StyleEjohwomu, O. A., Shamsideen Oshodi, O., Oladokun, M., Bukoye, O. T., Emekwuru, N., Sotunbo, A., & Adenuga, O. (2022). Modelling and Forecasting Temporal PM2.5 Concentration Using Ensemble Machine Learning Methods. Buildings, 12(1), 46. https://doi.org/10.3390/buildings12010046