Research on the Simplified Method of Nonlinear Finite Element Analysis for CFS-SPR Connections
Abstract
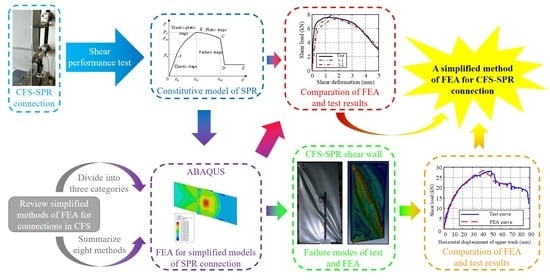
:1. Introduction
2. Shear Performance Test of the CFS-SPR Connection
2.1. Specimen Design
2.2. Test Set-Up and Loading Protocols
2.3. Test Results
2.3.1. Failure Modes and Mechanical Parameters
2.3.2. Failure Mechanism of the CFS-SPR Connection
3. Simplified Methods of Nonlinear FEA Applied to the CFS-SPR Connection
3.1. Boundary Conditions
3.2. Material Properties
3.3. Shear Constitutive Model of the CFS-SPR Connection
3.4. Simplified Methods of FEA
4. Simplified Analysis Results and Verification of Nonlinear FEA Model for the CFS-SPR Connection
4.1. Simplified Analysis Results
- (1)
- The first type of finite element models that used the coupling of the equivalent surface area to simplify the simulation could accurately simulate the failure characteristics of the SPR connection. The shear load–deformation curves in the elastic stage were highly similar to the test results, but its calculations in the plastic and failure stage are difficult to converge. In addition, the load–deformation curve of model 1-1 indicated that the hard contact between the sheets had a more obvious plastic stage.
- (2)
- The second type of three finite element models that used a constraint element to simplify modeling had a poor simulation effect on the failure characteristics of the SPR connection. There were large differences in the shear load–deformation curves of the three models, especially model 2-2 with the MPC-beam element. The shear load–deformation curve of the MPC-Pin element model was similar to the test results in the elastic, elastic–plastic and plastic stage, but that was quite different from the test results in the failure stage. For model 2-3 of the Fastener element, the shear load–deformation curve was similar to the test results in the elastic and plastic stage, but that was quite different from the test results in the elastic–plastic and failure stage.
- (3)
- The third type of two finite element models that used a link element to simplify modeling could simulate the failure characteristics of the SPR connection very accurately. The shear load–deformation curves of the numerical simulation were in good agreement with the test results in the elastic, elastic–plastic, plastic, and failure stages.
4.2. Verification of Analysis Results
5. Feasibility Verification of the Simplified Analysis Method of SPR Connection in the CFS Shear Wall
5.1. Shear Performance Test of the CFS Shear Wall with SPR
5.2. Finite Element Models of CFS Shear Wall with SPR
5.3. Comparison of Test and FEA Results
5.3.1. Comparison of Failure Modes
5.3.2. Comparison of Load–Displacement Curves
5.3.3. Comparison of Eigenvalue
6. Conclusions
- (1)
- The main failure modes of the CFS-SPR connection under shear loading were the pull-out of the rivet tail from the bottom sheet and the pull-over of the rivet head from the top sheet.
- (2)
- According to the different transmitting methods of shear force, the nonlinear simplified FEA methods applied to the CFS-SPR connection could be divided into three types: the shearing force was transmitted through the equivalent surface coupling, the shearing force was transmitted by the constraint element between the nodes, and the shearing force was transmitted through the link element between the nodes in the connection area.
- (3)
- The simplified analysis method of the equivalent surface coupling was only suitable for studying the local mechanical performance and failure characteristics of the SPR joint. The constraint element Pin and Fastener were suitable for simulating the mechanical properties of the SPR connection that had not reached the failure stage, while the constraint element Beam was not suitable for the nonlinear simplified FEA of the SPR. The link element Cartesian connector and the spring element Spring2 were suitable for simulating the mechanical performance of overall members with the SPR connection, and the Cartesian connector had higher calculation efficiency and accuracy than Spring2.
- (4)
- The SPR connection in the CFS frame could be simplified by the constraint element Pin or the fastener element Fastener, while the SPR connection between the CFS frame and steel sheathing could be simplified by using the link element Cartesian connector and the spring element Spring2.
- (5)
- Based on the nonlinear simplified analysis method of the CFS-SPR connection, the finite element model of the shear wall had high reliability and was satisfied to the calculation accuracy required in the field of civil engineering. Therefore, the simplified method of nonlinear FEA for CFS-SPR connection proposed in this paper could provide an effective reference for the simulation of the SPR connection in thin-walled steel structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guan, Y.; Zhou, X.H.; Yao, X.M.; Shi, Y. Seismic performance of prefabricated sheathed cold-formed thin-walled steel buildings: Shake table test and numerical analyses. J. Constr. Steel Res. 2020, 167, 105837. [Google Scholar] [CrossRef]
- Wu, J.L.; Chen, C.; Ouyang, Y.W.; Qin, D.L.; Li, H.J. Recent development of the novel riveting processes. Int. J. Adv. Manuf. Technol. 2021, 117, 19–47. [Google Scholar]
- Xie, Z.Q.; Zhang, A.L.; Yan, W.M.; Zhang, Y.X.; Mu, T.T.; Yu, C. Study on shear performance and calculation method for self-pierce riveted joints in galvanized steel sheet. Thin Walled Struct. 2021, 161, 107490. [Google Scholar] [CrossRef]
- Zhang, A.L.; Xie, Z.Q.; Yan, W.M.; Zhang, Y.X.; Zhou, D.X. Experimental investigation of CFS steel sheathed shear walls with openings using self-piercing rivets. Thin Walled Struct. 2019, 138, 313–325. [Google Scholar] [CrossRef]
- Atzeni, E.; Ippolito, R.; Settineri, L. Experimental and numerical appraisal of self-piercing riveting. CIRP Ann. Manuf. Technol. 2009, 58, 17–20. [Google Scholar] [CrossRef]
- Coppieters, S.; Lava, P.; Baes, S.; Sol, H.; Houtte, P.V.; Debruyne, D. Analytical method to predict the pull-out strength of clinched connections. Thin Walled Struct. 2012, 52, 42–52. [Google Scholar]
- Mucha, J. The failure mechanics analysis of the solid self-piercing riveting joints. Eng. Fail. Anal. 2015, 47, 77–88. [Google Scholar] [CrossRef]
- He, X.C.; Gu, F.S.; Ball, A.; Wahab, M.A. Fatigue behaviour of fastening joints of sheet materials and finite element analysis. Adv. Mech. Eng. 2013, 5, 658219. [Google Scholar] [CrossRef]
- Acharya, S.R.; Sivakumaran, K.S. Finite element models for thin-walled steel member connections. Int. Sch. Res. Not. 2012, 2012, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Atsushi, K.; Toshiyuki, K.; Kanda, A. A simplified finite element model of riveted joints for structural analyses with consideration of nonlinear load-transfer characteristics. Aerospace 2021, 8, 196. [Google Scholar]
- Bier, M.; Sommer, S. Advanced investigations on a simplified modeling method of self-piercing riveted joints for crash simulation. In Proceedings of the 11th LS-DYNA Forum, Ulm, Germany, 8–10 October 2012. Available online: https://www.dynamore.de/de/download/papers/ls-dyna-forum-2012 (accessed on 8 October 2022).
- Hanssen, A.G.; Olovsson, L.; Porcaro, R.; Langseth, M. A large-scale finite element point-connector model for self-piercing rivet connections. Eur. J. Mech. A Solids 2010, 29, 484–495. [Google Scholar] [CrossRef]
- Dourado, M.D.M.; Meireles, J.F.B. A simplified finite element riveted lap joint model in structural dynamic analysis. Adv. Mater. Res. 2014, 1016, 185–191. [Google Scholar]
- Dubina, D. Behavior and performance of cold-formed steel-framed houses under seismic action. J. Constr. Steel Res. 2008, 64, 896–913. [Google Scholar] [CrossRef]
- Fülöp, L.A.; Dubina, D. Design criteria for seam and sheeting-to-framing connections of cold-formed steel shear panels. J. Struct. Eng. 2006, 132, 582–590. [Google Scholar] [CrossRef]
- Shi, Y.L.; Jin, Y.; Zhang, P.P.; Wang, W.D. Research on shear resistance of cold-formed steel stud composite walls. Adv. Mater. Res. 2011, 1269, 243–249. [Google Scholar] [CrossRef]
- Derveni, F.; Gerasimidis, S.; Schafer, B.W.; Peterman, K.D. High-fidelity finite element modeling of wood-sheathed cold-formed steel shear walls. J. Struct. Eng. 2021, 147, 04020316. [Google Scholar] [CrossRef]
- Muthuraman, M.; Anuradha, R.; Awoyera, P.O.; Gobinath, R. Numerical simulation and specification provisions for buckling characteristics of a built-up steel column section subjected to axial loading. Eng. Struct. 2020, 207, 110256. [Google Scholar] [CrossRef]
- Ngo, H.H. Numerical and experimental studies of wood sheathed cold-formed steel framed shear walls. Johns Hopkins Univ. 2014. Available online: http://jhir.library.jhu.edu/handle/1774.2/37082 (accessed on 8 October 2022).
- Šedek, J.; Růžek, R. Magna-Lok rivet joint and the stiffness-equivalent FE model. Aircr. Eng. Aerosp. Technol. 2019, 91, 834–842. [Google Scholar] [CrossRef]
- Niari, S.E.; Rafezy, B.; Abedi, K. Seismic behavior of steel sheathed cold-formed steel shear wall: Experimental investigation and numerical modeling. Thin Walled Struct. 2015, 96, 337–347. [Google Scholar] [CrossRef]
- Attari, N.K.A.; Alizadeh, S.; Hadidi, S. Investigation of CFS shear walls with one and two-sided steel sheeting. J. Constr. Steel Res. 2016, 122, 292–307. [Google Scholar] [CrossRef]
- Borzoo, S.; Ghaderi, S.R.M.; Mohebi, S.; Rahimzadeh, A. Nonlinear finite element modeling of steel-sheathed cold-formed steel shear walls. Steel Compos. Struct. 2016, 22, 70–89. [Google Scholar]
- JGJ 227-2011; China Industry Standard, Technical Specification for Low-Rise Cold-Formed Thin-Walled Steel Buildings. Architecture & Industry Press of China: Beijing, China, 2011.
- GB/T 228.1-2010; China National Standard, Metallic Materials-Tensile Testing—Part 1: Method of Test at Room Temperature. Standardization Administration of China: Beijing, China, 2011.
- Tan, J.; Gu, C.W.; Su, M.N.; Wang, Y.H.; Wang, K.; Shi, Y.; Lan, Y.S.; Luo, W.; Deng, X.W.; Bai, Y.T.; et al. Finite element modelling and design of steel plate shear wall buckling-restrained by hat-section cold-formed steel members. J. Constr. Steel Res. 2020, 174, 106274. [Google Scholar]
- Xie, Z.Q.; Yan, W.M.; Yu, C.; Mu, T.T.; Song, L.L. Experimental investigation of cold-formed steel shear walls with self-piercing riveted connections. Thin Walled Struct. 2018, 131, 1–15. [Google Scholar]





















| Steel Sheet Combination | Length of Rivet | Inner Diameter of Die | Depth of Die | Height of Die Pip |
|---|---|---|---|---|
| l/(mm) | D/(mm) | h/(mm) | H/(mm) | |
| S0.8 + 0.8 | 4.0 | 7.0 | 1.70 | 1.70 |
| S1.0 + 1.0 | 4.5 | 7.0 | 1.70 | 1.70 |
| S1.2 + 1.2 | 5.0 | 9.0 | 1.85 | 0.55 |
| S1.5 + 1.5 | 6.0 | 9.0 | 1.85 | 0.55 |
| S0.8 + 1.5 | 4.5 | 9.0 | 1.85 | 0.55 |
| S1.0 + 1.5 | 5.0 | 9.0 | 1.85 | 0.55 |
| Specimen Number | Mean Maximum Shear Load | Mean Maximum Displacement | Failure Modes |
|---|---|---|---|
| Pu/(kN) | /(mm) | ||
| S0.8 + 0.8 | 3.544 | 1.023 | I |
| S1.0 + 1.0 | 4.570 | 1.063 | I |
| S1.2 + 1.2 | 6.344 | 1.121 | I |
| S1.5 + 1.5 | 7.348 | 1.151 | I |
| S0.8 + 1.5 | 4.338 | 1.180 | II |
| S1.0 + 1.5 | 5.457 | 1.722 | II |
| Steel Sheet | fy | fu | fu/fy | E | S |
|---|---|---|---|---|---|
| (t = 1.5 mm) | (MPa) | (MPa) | (GPa) | (%) | |
| Sample 1 | 255.81 | 354.84 | 1.39 | 2.06 | 30.9 |
| Sample 2 | 237.53 | 347.85 | 1.46 | 2.00 | 31.2 |
| Sample 3 | 280.64 | 361.29 | 1.29 | 2.15 | 32.1 |
| Average | 258.00 | 354.66 | 1.38 | 2.07 | 31.4 |
| Steel Sheet | fy | fu | fu/fy | E | S |
|---|---|---|---|---|---|
| (t = 0.8 mm) | (MPa) | (MPa) | (GPa) | (%) | |
| Average | 267.68 | 361.96 | 1.35 | 2.03 | 26.6 |
| Number | Simplified Sketch | Simplified Methods of Finite Element Model |
|---|---|---|
| 1-1 |  | The shearing behavior is equivalent to the shearing force between two rigid connecting surfaces (Area binding Tie), and assuming there is no relative movement and deformation in the binding area. The frictionless hard contact between two steel sheets is considered. |
| 1-2 |  | The modeling method is the same as model 1-1, but the contact between the two steel sheets is ignored. |
| 1-3 |  | The shearing behavior is equivalent to the shearing force between two coupling surfaces (Area Coupling), and the shear area between the two steel sheets is coupled to the same reference point. It is assumed that relative movement and deformation can occur in the coupling area, and the contact between the two steel sheets is ignored. The remaining parameters are the same as model 1-1. |
| Number | Simplified Sketch | Simplified Methods of Finite Element Model |
|---|---|---|
| 2-1 |  | The rivet is simplified into a multipoint constraint element (MPC-pin), and its shear behavior is equivalent to the shearing force of the constraint element between two points [17]. The connection between the two reference points is assumed to be hinged, and the contact between the two steel sheets is ignored. |
| 2-2 |  | The rivet is simplified into a multipoint constraint element (MPC-Beam), assuming that the connection between the two reference points is rigid [18]. The remaining parameters are the same as model 2-1. |
| 2-3 |  | The rivet is simplified into a fastener element (Fastener), assuming that the connection between the two reference points is rigid [21]. The remaining parameters are the same as model 2-1. |
| Number | Simplified Sketch | Simplified Methods of Finite Element Model |
|---|---|---|
| 3-1 |  | The rivet is simplified into a Cartesian connector element, and its shearing behavior is equivalent to the shearing force of the connector element between two points [22]. The connector element can set the relative relationship of three translational and three rotational degrees of freedom between two points [23]. The contact between the two steel sheets is ignored. |
| 3-2 |  | The rivet is simplified into a spring element (Spring2). The shearing area is simplified into two nodes, and its shear behavior is equivalent to the shearing force of the spring between the two points [10]. The Spring2 element can set parameters for the three orthogonal directions by setting up a local coordinate system. The remaining parameters are the same as for model 3-1. |
| Number | Complexity Degree of Model | Complexity Degree of Mesh | Similarity Degree of Failure Modes | Calculation Time (s) |
|---|---|---|---|---|
| 1-1 | ★★★★ | ★★★★ | ★★★★ | 127 |
| 1-2 | ★★★ | ★★★★ | ★★★★ | 71 |
| 1-3 | ★★★ | ★★★★ | ★★★ | 58 |
| 2-1 | ★ | ★ | ★ | 23 |
| 2-2 | ★ | ★ | ★★ | 25 |
| 2-3 | ★★ | ★ | ★★★ | 43 |
| 3-1 | ★ | ★ | ★ | 10 |
| 3-2 | ★★ | ★ | ★ | 18 |
| Number | Ke/Ktest | Pu/Ptest | εm/εtest | εc (mm) |
|---|---|---|---|---|
| 1-1 | 0.79 | 1.14 | 1.08 | 3.42 |
| 1-2 | 0.61 | 1.05 | 0.80 | 2.00 |
| 1-3 | 0.46 | 0.95 | 1.17 | 2.22 |
| 2-1 | 0.90 | 1.09 | 3.38 | 4.32 |
| 2-2 | 0.92 | 1.80 | 1.02 | 1.53 |
| 2-3 | 0.43 | 1.19 | 0.98 | 4.42 |
| 3-1 | 0.86 | 1.04 | 1.14 | 5.00 |
| 3-2 | 0.74 | 0.97 | 1.58 | 5.00 |
| Specimen Number | Results | Yield Displacement Δy | Yield Load Py | Maximum Displacement Δmax | Maximum Load Pmax | Shear Stiffness Ke | Shear Capacity Ps |
|---|---|---|---|---|---|---|---|
| (mm) | (kN) | (mm) | (kN) | (kN/m) | (kN/m) | ||
| W-1 | FEA | 13.10 | 24.03 | 42.49 | 28.37 | 1.84 | 23.64 |
| Test results | 14.66 | 24.11 | 48.41 | 27.98 | 1.64 | 23.32 | |
| Error (%) | 10.64 | 0.33 | 12.23 | 1.39 | 12.20 | 1.39 | |
| W-2 | FEA | 8.54 | 17.96 | 22.54 | 20.74 | 1.82 | 17.28 |
| Test results | 7.95 | 17.43 | 26.19 | 20.63 | 1.85 | 17.19 | |
| Error (%) | 7.42 | 3.04 | 13.94 | 0.53 | 1.62 | 0.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, A.; Xie, Z.; Shi, L.; Zhang, Y.; Zhou, D.; Zhang, X. Research on the Simplified Method of Nonlinear Finite Element Analysis for CFS-SPR Connections. Buildings 2022, 12, 1925. https://doi.org/10.3390/buildings12111925
Zhang A, Xie Z, Shi L, Zhang Y, Zhou D, Zhang X. Research on the Simplified Method of Nonlinear Finite Element Analysis for CFS-SPR Connections. Buildings. 2022; 12(11):1925. https://doi.org/10.3390/buildings12111925
Chicago/Turabian StyleZhang, Ailin, Zhiqiang Xie, Leilei Shi, Yanxia Zhang, Daxing Zhou, and Xiangdong Zhang. 2022. "Research on the Simplified Method of Nonlinear Finite Element Analysis for CFS-SPR Connections" Buildings 12, no. 11: 1925. https://doi.org/10.3390/buildings12111925
APA StyleZhang, A., Xie, Z., Shi, L., Zhang, Y., Zhou, D., & Zhang, X. (2022). Research on the Simplified Method of Nonlinear Finite Element Analysis for CFS-SPR Connections. Buildings, 12(11), 1925. https://doi.org/10.3390/buildings12111925