Interpretation of Machine-Learning-Based (Black-box) Wind Pressure Predictions for Low-Rise Gable-Roofed Buildings Using Shapley Additive Explanations (SHAP)

Abstract

Conventional methods of estimating pressure coefficients of buildings retain time and cost constraints. Recently, machine learning (ML) has been successfully established to predict wind pressure coefficients. However, regardless of the accuracy, ML models are incompetent in providing end-users’ confidence as a result of the black-box nature of predictions. In this study, we employed tree-based regression models (Decision Tree, XGBoost, Extra-tree, LightGBM) to predict surface-averaged mean pressure coefficient (C_p,mean), fluctuation pressure coefficient (C_p,rms), and peak pressure coefficient (C_p,peak) of low-rise gable-roofed buildings. The accuracy of models was verified using Tokyo Polytechnic University (TPU) wind tunnel data. Subsequently, we used Shapley Additive Explanations (SHAP) to explain the black-box nature of the ML predictions. The comparison revealed that tree-based models are efficient and accurate in wind-predicting pressure coefficients. Interestingly, SHAP provided human-comprehensible explanations for the interaction of variables, the importance of features towards the outcome, and the underlying reasoning behind the predictions. Moreover, SHAP confirmed that tree-based predictions adhere to the flow physics of wind engineering, advancing the fidelity of ML-based predictions.

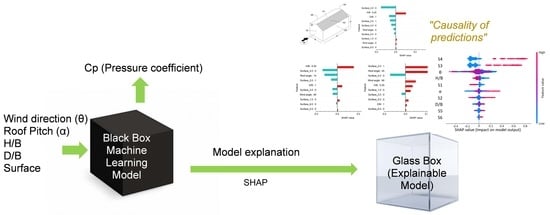
1. Introduction

Low-rise buildings are popular all over the world as they serve many sectors (e.g., residential, industrial, and commercial). Despite the ubiquitous presence, these buildings are constructed in various terrain profiles with numerous geometric configurations. From the wind engineering viewpoint, these buildings are located in the ABL with high turbulence intensities and steep velocity gradients. As a result, external wind pressure on low buildings is spatially and temporally heterogeneous. Either physical experiments (full scale or wind tunnel) or CFD simulations are often employed to investigate external pressure characteristics of low buildings. In the experiments, external pressure coefficients are recorded to investigate the external wind pressure on the building envelope. These pressure coefficients are required to estimate design loads and for natural ventilation calculations. External pressure coefficients indicate the building components that are subjected to large suction loads. However, these methods are resource-intensive and require time and significant expertise. Despite being computationally expensive, numerical simulations such as CFD are widely used for ABL modeling [1,2,3,4,5].

Alternatively, secondary methods including analytical models and parametric equations were developed in numerous ways. For example, DAD methods were introduced to ensure that structural designs are economical and safe [6,7,8]. Swami and Chandra [9] established a parametric equation to estimate C_p,mean on walls of low-rise buildings. Subsequently, Muehleisen and Patrizi [10] developed a novel equation to improve the accuracy of the same predictions. However, both equations are permitted only for rectangular-shaped buildings and failed to predict the pressure coefficients of the roof. In consequence, the research community explored advanced data-driven methods and algorithms as an alternative.

Accordingly, a noticeable surge in ML-based modeling is observed in engineering applications. Foremost, these approaches can be categorized into supervised, semi-supervised, and unsupervised ML, based on data-labeling [11,12]. Regardless of the complexity of the approach, various ML algorithms are successively employed in structural engineering applications as evident from the comprehensive review provided by Sun et al. [13]. In addition, many recent studies combined ML techniques with building engineering [14,15,16,17,18,19,20,21,22,23,24,25,26]. For example, Wu et al. [27] used tree-based ensemble classifiers to predict hazardous materials in buildings. Fan and Ding [28] developed a scorecard for sick building syndrome using ML. Ji et al. [29] used ML to investigate life cycle cost and life cycle assessment of buildings. In their proposed work, deep learning models showed superior performance. Overall models achieved an R² between 0.932 and 0.955. Yang et al. [30] reported that supervised classification methods can be effectively used for building climate zoning. Olu-Ajyal et al. [31] argued that deep neural networks perform better compared to remaining machine learning models (Artificial Neural Network, Gradient Boosting, Decision Tree, Random Forest, Support Vector Machine, Stacking, K-Nearest Neighbour, and Linear Regression) in predicting building energy consumption in residential buildings.

Given its ability to find non-linear and complex functions, Kareem [32] stated that ML algorithms are competent with physical experiments and numerical simulations when predicting wind loads on buildings. Numerous studies have been conducted over the years on investigating ML applications in wind engineering [14,33,34,35,36,37,38,39,40,41,42,43,44]. For example, Bre et al. [33] and Chen et al. [35] developed ANN models to predict wind pressure coefficients of low-rise buildings. Lin et al. [45] suggested an ML-based method to estimate the cross-wind effect of tall buildings. They used lightGBM regression to predict crosswind spectrum, and it achieved an acceptable accuracy, complying with experimental results. Kim et al. [46] proposed clustering algorithms to identify wind pressure patterns. They noticed that the clustering algorithm reasonably captures the pressure patterns better than independent component analysis or principal component analysis. Dongmei et al. [36], and Duan et al. [37] used ANNs to predict wind loads and wind speeds, respectively. Hu and Kwok [40] proposed data-driven (tree-based) models to predict wind pressure around circular cylinders. Accordingly, all tree-based models achieved R² > 0.96 for predicting mean pressure coefficients and R² > 0.97 for predicting fluctuation (rms) pressure coefficients. Hu et al. [47] investigated the applicability of machine learning models (Decision Tree, Random Forest, XGBoost, GAN) to predict wind pressure of tall buildings in the presence of interference-effect. The proposed GAN showcased superior performance in contrast to the remaining models. The GAN achieved R² = 0.988 for mean pressure coefficient predictions and R² = 0.924 for rms pressure coefficient predictions. Wang et al. [48] integrated LSTM, Random Forests, and gaussian process regression to predict short-term wind gusts. They argued that the proposed ensemble method is more accurate than employing individual models. Tian et al. [49] introduced a novel approach using deep neural networks (DNN) to predict wind pressure coefficients of low-rise gable-roofed buildings. The method achieved R = 0.9993 for mean pressure predictions and R = 0.9964 for peak pressure predictions. In addition, Mallick et al. [50] extended experiments from regular-shaped buildings to unconventional configurations while combining gene expression programming and ANNs. The proposed equation was intended to predict surface average pressure coefficients of a C-shaped building. Na and Son [51] predicted the atmospheric motion vector around typhoons using GAN, and the model achieved acceptable accuracy (R² > 0.97). Lamberti and Gorle [44] reported that ML can balance computation cost and accuracy in predicting complex turbulent flow quantities. Recent work done by Arul et al. [52] proposed that shapelet transformation is an effective way to represent the time series of wind. They observed that shapelet transformation is useful in identifying a wide variety of thunderstorms that cannot be detected using conventional gust factor-based methods. Interestingly, these ML models were precise and less time-consuming in contrast to conventional methods.

However, all related studies failed to explain the black-box nature of ML predictions and their underlying reasoning. ML models estimate complex functions while no insights on its inner-working methodology are provided to the end-user. Regardless of its superior performance, model transparency is inferior compared to traditional approaches. The absence of such knowledge makes implementing ML in wind engineering more difficult. For instance, end-users are confident in physical and CFD modeling as a result of the transparency of the process. Hence, ML models should be explainable in order to obtain the trust of domain experts and end-users.

As an emerging branch, explainable artificial intelligence expects to overcome the black-box nature of ML predictions. It provides insights into how an ML model performs the prediction and the causality of prediction. It works as the human agent of the ML model. Therefore, it is highly recommended among multi-stakeholders [53]. Explainable ML makes regular ML predictions interpretable to the end-user. In addition, end-users become aware of the form of relationship that exists between features. Hence, it is convenient for the user to understand the importance of the features, and the dependency among various features as a model in whole or instances [54,55,56]. With such advanced features, explainable ML turns black-box models into glass-box models. One such attempt has been recently given to predict the external pressure coefficients of a low-rise flat-roofed building surrounded by similar buildings by using explainable machine learning [57]. They argued that explainable models advance the ML models by revealing the causality of predictions. However, that study focused on the effect of surrounding buildings, whereas the present study focused on isolated gable-roofed low-rise buildings and the effect of its geometric parameters.

Therefore, the main objective is to predict surface-averaged pressure coefficients of low-rise gable-roofed buildings using explainable ML. We argue that explainable ML improves the transparency of the pressure coefficient predictions while exposing the inner-working of the model. On the other hand, the explainable ML is imperative to cross-validate the predictions using theoretical/experimental knowledge on low-rise gable-roofed buildings. Finally, the study demonstrates that using explainable ML to predict wind pressure coefficient does not affect model complexity or accuracy but rather enhances the fidelity by improving end users’ trust in predictions.

Because the wind engineering community is new to explainable ML, Section 2 provides a brief on the concept and the explanation we used (Shapley additive explanations (SHAP) [58]). Section 3 provides the background of tree-based ML models used in this study. Section 4 and Section 5 provide the performance analysis and the methodology of the study, respectively. Results and discussion are provided in Section 6 and Section 7 concludes the paper. Section 8 discusses the limitations and future work of the research study.

2. Explainable ML

Explainable ML does not own a standard definition. Explainable methods can be categorized into unique approaches namely, intrinsic and post hoc. For example, models whose structure is simple are self-explainable (intrinsic) (e.g., linear regression, Decision Trees at lower tree depths). However, when an ML model is complex, a post hoc explanation (explainable ML) is required to elucidate the predictions

Several models are already available that provide post hoc explanations. These include models such as DeepLIFT [59], LIME [60], RISE [61], and SHAP [58]. LIME and SHAP have been widely used in ML applications. However, Moradi and Samwald [62] state LIME creates dummy instances considering the neighborhood of an instance by approximating a linear behavior. Therefore, LIME interpretations do not reflect actual feature values. In this study, we used SHAP to investigate the influence of each parameter on respective prediction, its quantification, and convince underlying reasoning behind instances.

Shapley Additive Explanations (SHAP)

SHAP provides both local and global explanations of an ML model [63]. The value assigned by SHAP can be used as a unified measure of feature importance. SHAP follows core concepts in game theory when computing the feature importance. For instance, “games” can be referred to as model predictions, and features inside the ML model are represented by “players”. Simply, SHAP quantifies the contribution of each player to the game [58]. Global interpretation provided by SHAP measures how a patient attribute contributes to a prediction. Liang et al. [54] provided a detailed classification of explanation models, in which SHAP is a data-driven and perturbation-based method. Therefore, it relies on input parameters and does not require understanding the operation sequence of the ML model.

Perturbation works by masking several regions of the data samples to create disturbances. Subsequently, a disordered sample will result in another set of predictions that can be compared with the original predictions. Lundberg and Lee [58] introduced unique SHAP versions (e.g., DeepSHAP, Kernel SHAP, LinearSHAP, and TreeSHAP) for specific ML model categories. For example, the current study employed TreeSHAP for ML predictions. There, a linear explanatory model is used and the corresponding Shapley value is calculated using Equation (1),

$$\mathrm{f}\left({\mathrm{y}}^{\prime }\right)={ф}_{\mathrm{o}}+{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{ф}_{\mathrm{i}}{{\mathrm{y}}^{\prime }}_{\mathrm{i}}$$

(1)

where f denotes the explanation model whereas ${\mathrm{y}}^{\prime }\in {\{0,1\}}^{\mathrm{N}}$ denotes the simplified features of the coalition vector. N and $ф\in ℝ$ denote the maximum size of the coalition and the feature attribution, respectively. Lundberg and Lee [58] specified Equations (2) and (3) to compute feature attribution,

$${ф}_{\mathrm{i}}={\displaystyle \sum }_{\mathrm{S} \left\{1,\dots ,\mathrm{p}\right\}\backslash \left\{\mathrm{i}\right\}}\frac{\left|\mathrm{S}\right|!\left(\mathrm{p}-\left|\mathrm{S}\right|-1\right)!}{\mathrm{p}!}\left[{\mathrm{g}}_{\mathrm{x}}\left(\mathrm{S}{\displaystyle \cup }\left\{\mathrm{i}\right\}\right)-{\mathrm{g}}_{\mathrm{x}}\left(\mathrm{S}\right)\right]$$

(2)

$$\mathrm{where}; {\mathrm{g}}_{\mathrm{x}}\left(\mathrm{S}\right)=\mathrm{E}\left[\mathrm{g}\left(\mathrm{x}\right)│{\mathrm{x}}_{\mathrm{S}}\right]$$

(3)

In Equation (2), S represents a subset of the features (input) and x is the vector of feature values of the instance to be interpreted. Thus, the Shapley value is denoted through a value function $({\mathrm{g}}_{\mathrm{x}}$). Here, p symbolizes the number of features and ${\mathrm{g}}_{\mathrm{x}}\left(\mathrm{S}\right)$ is the prediction obtained from features in S. $\mathrm{E}[\mathrm{g}\left(\mathrm{x}\right)│{\mathrm{x}}_{\mathrm{K}}]$ represents the expected value of the function on subset S. In addition, this study employs Scikit-learn (Sklearn), NumPy, matplot, pandas, and Shap libraries for the implementation.

Sklearn is the most efficient and robust library that is used for machine learning applications in python. Sklearn allows using numerous machine learning tools, including regression, classification, clustering, and dimensionality reduction. In addition, this library was written mostly using python over Numpy, Scipy, and Matplotlib.

3. Tree-Based ML Algorithms

We proposed four tree-based ML models for the present study. All four models are Decision Tree-based models. Tree-based models follow a deterministic process in decision-making. Patel and Prajapati [64] reported that a Decision Tree mimics the human thinking process. Despite the complexity that grows with tree-depth, the decision-tree structure is self-explainable. Moreover, tree-based models work efficiently for structured data.

3.1. Decision Tree Regressor

Decision Trees serve for both regression and classification problems [65,66,67]. The working principle of a Decision Tree is to split a comprehensive task into several simplified versions. Evolved structure of the Decision Tree is hierarchical from roots to end leaves and generates a model based on logical postulations that can be subsequently employed to predict new data.

Recursive breakdown and multiple regression are performed to train a decision-tree regression model. Until end criteria are met, splitting takes place at each interior node, starting from the root node of a Decision Tree. Primarily, each leaf node of the tree represents a simple regression model. Trimming low information gain branches (pruning) is applied to enhance the generalization of the model. Furthermore, the Decision Tree compacts each possible alternative toward the conclusion.

Per each partition, the response variable y is separated into two sets, namely, S₁ and S₂. Subsequently, the Decision Tree examines a predictor variable x concerning the split threshold,

$$SSE={\displaystyle \sum }_{i\in S_1}{\left(y_i-\overline{y_1}\right)}^2+{\displaystyle \sum }_{i\in S_2}{\left(y_i-\overline{y_2}\right)}^2$$

(4)

$\mathrm{where} \overline{y_1}$ and $\overline{y_2}$ are the average values of the response for each set. The tree generally intends to minimize the sum of squared error (SSE) (refer to Equation (4)) for each split. The tree starts growing with recursive splits and split thresholds. The terminal node represents the average of y values of samples collected within the node.

3.2. XGBoost Regressor

XGBoost is a gradient boosting implementation that boosts weak learners. It is more often preferred due to its fast execution process [68]. Chakraborty and Elzarka [69], Mo et al. [70], and Xia et al. [69,70,71] have successfully used XGBoost in their respective studies. The regressor itself can handle overfitting or underfitting issues, and regularizations are better than Decision Tree and Random Forest algorithms.

The regularization function of XGBoost assists to control the complexity of the model and to select predictive functions. The objective function is defined as a regularization term together with a loss function and it is optimized using gradient descent. XGBoost provides column subsampling compared to conventional Gradient Boosting [72]. At each level, the tree structure is formed by estimating leaf score, objective function, and regularization. Hence, it is difficult to evaluate all possible combinations at the same time. Subsequently, the tree structure will be re-employed in an iterative manner that helps to reduce computational expense. Information gain at each node is estimated during the splitting process and seeks the best splitting node until it reaches maximum depth. Later, the pruning process is executed in bottom-up order. The objective function in terms of loss and regularization can be expressed as given in Equation (5),

$$\mathrm{objective}={\displaystyle \sum }_{j=1}^{N}l(y_j,{\widehat{y}}_j)+{\displaystyle \sum }_{j=1}^K\Omega \left(f_j\right)$$

(5)

The summation (${\displaystyle {\displaystyle \sum }_{j=1}^N}l(y_j,\widehat{y_j})$) is the loss function that represents the difference between predicted $({\widehat{y}}_j)$ and actual values $(y_j)$. The summation (${\displaystyle {\displaystyle \sum }_{j=1}^K}\Omega \left(f_j\right)$) is the regularization term that decides the complexity of XGBoost model.

3.3. Extra-Tree Regressor

Extra-tree regressor is classified under ensemble methods of supervised learning [73,74,75]. It builds random trees whose primary structure is independent of the outcome of the learning sample. Okoro et al. [74] stated randomized trees are adopted for numerical inputs that improve precision and substantial reduction in computational burden.

Extra-tree regressor follows the classical top-down approach to fit disarrayed Decision Trees on subsamples of learning data. Random split points make the extra-tree regressor unique from other tree-based ensembles. Afterward, the tree grows using the whole learning sample. In particular, final predictions are done using a voting process in classification and regression. John et al. [76] and Seyyedattar et al. [77] described random subset features and detailed structure and their importance, respectively. Interestingly, explicit randomization can reduce similarities in contrast to weaker randomization of other methods.

For regression, relative variance reduction is used, and the score is expressed in Equation (6). The terms U_i and U_j represent subsets of cases from U that correspond to the outcome of a splits,

$${\mathrm{Score}}_{\mathrm{R}}\left(\mathrm{s}, \mathrm{U}\right)=\frac{\mathrm{var}\left\{\mathrm{y}|\mathrm{U}\right\}-\frac{\left|{\mathrm{U}}_{\mathrm{i}}\right|}{\left|\mathrm{U}\right|}\mathrm{var}\left\{{\mathrm{y}|\mathrm{U}}_{\mathrm{i}}\right\}-\frac{\left|{\mathrm{U}}_{\mathrm{j}}\right|}{\left|\mathrm{U}\right|}\mathrm{var}\left\{{\mathrm{y}|\mathrm{U}}_{\mathrm{j}}\right\}}{\mathrm{var}\left\{\mathrm{y}|\mathrm{U}\right\}}$$

(6)

3.4. LightGBM Regressor

LightGBM is an efficient gradient boosting structure formed on boosting and Decision Trees [78,79,80]. It uses histogram-based algorithms in contrast to XGBoost, to accelerate the training process, reducing memory consumption. Given that Decision Tree itself is a weak model, the accuracy of the segmentation point is not important. A coarse segmentation process can influence the regularization effect that avoids over-fitting. Leaf orientation at the downside can grow deeper Decision Trees leading to over-fitting situations. Hence, LightGBM tackles this issue by constricting maximum depth to the top of leaves. The model not only enables a higher efficiency but also handles non-linear relationships, ensuring a higher precision.

4. Model Performance

The following analysis was carried out to evaluate the performance of predictions obtained from machine learning models.

Performance Evaluation

Ebtehaj et al. [81] specified several indices to compare model efficiencies in terms of predictions. Hyperparameter optimization and model training were performed based on R². For validation predictions, we proposed R, MAE, and RMSE. R² expresses how well predictions fit actual data. R closer to +1 or −1 indicates a strong positive or negative correlation, respectively. MAE evaluates direct residual between wind tunnel and ML predictions while RMSE considers standard deviation of residuals, indicating how far predictions lie from experimental values. These four indices are mathematically formulated as shown in Equations (7)–(10),

$${\mathrm{R}}^2=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\left({\mathrm{C}}_{\mathrm{p},\mathrm{ML}}-{ \overline{\mathrm{C}}}_{\mathrm{p},\mathrm{WT}}\right)}^2}{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\left({\mathrm{C}}_{\mathrm{p},\mathrm{WT}}-{ \overline{\mathrm{C}}}_{\mathrm{p},\mathrm{WT}}\right)}^2}=\frac{\mathrm{Model} \mathrm{Sum} \mathrm{of} \mathrm{Squares} \left(\mathrm{MSS}\right)}{\mathrm{Total} \mathrm{Sum} \mathrm{of} \mathrm{Squares} \left(\mathrm{TSS}\right)}$$

(7)

$$\mathrm{R}=\frac{\mathrm{N}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}\left({\mathrm{C}}_{\mathrm{p},\mathrm{WT}}.{\mathrm{C}}_{\mathrm{p},\mathrm{ML}}\right)-({{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{C}}_{\mathrm{p},\mathrm{WT}}.{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{C}}_{\mathrm{p},\mathrm{ML}})}{\sqrt{(\mathrm{N}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{C}}_{\mathrm{p},\mathrm{WT}}{}^2-{({{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{C}}_{\mathrm{p},\mathrm{WT}})}^2)}.\sqrt{\mathrm{N}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{C}}_{\mathrm{p},\mathrm{ML}}{}^2-{({{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{C}}_{\mathrm{p},\mathrm{ML}})}^2)}}$$

(8)

$$\mathrm{MAE}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}\left|{\mathrm{C}}_{\mathrm{p},\mathrm{WT}}-{\mathrm{C}}_{\mathrm{p},\mathrm{ML}}\right|}{\mathrm{N}}$$

(9)

$$\mathrm{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{({\mathrm{C}}_{\mathrm{p},\mathrm{WT}}-{\mathrm{C}}_{\mathrm{p},\mathrm{ML}})}^2}{\mathrm{N}}}$$

(10)

N denotes the number of data samples and subscripts WT and ML refer to “Wind Tunnel” and “ML” predictions, respectively. C_p represents all three predicting variables, including mean, fluctuating (rms), and peak (minimum) components. ${ \overline{\mathrm{C}}}_{\mathrm{P}}$ refers to the average value of the dependent variable in the validation data set.

5. Methodology

For each ML application, the quality and reliability of training data are very crucial. In terms of wind engineering applications, data sets should consist of a wide range of geometric configurations with multi parameters to obtain a generalized solution. The explanation becomes more comprehensible with a wide range of parameters.

Several wind tunnel databases are freely available for reference. NIST [82] and TPU [83] databases are well-known as reliable databases, especially for bluff body aerodynamics related to buildings. Both databases provide time histories of wind pressure including various geometric configurations of buildings. However, TPU provides wind tunnel data of gable-roofed low-buildings involving a wide range of roof pitches. Therefore, the TPU data set was selected for the application purpose.

Mean, fluctuating, and peak pressure coefficients on the corresponding surface were averaged and denoted as surface averaged pressure coefficients. Equations (11)–(14) were used to calculate the pressure coefficients from the time histories. It is noteworthy that the experiments had been conducted under fixed wind velocity. Therefore, the study cannot assess the effect of approaching wind velocity.

$${\mathrm{C}}_{\mathrm{p},\mathrm{mean}}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{C}}_{\mathrm{p},\mathrm{i}}}{\mathrm{n}}$$

(11)

$${\mathrm{C}}_{\mathrm{p},\mathrm{rms}}=\sqrt{\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{({\mathrm{C}}_{\mathrm{p},\mathrm{i}}-{\mathrm{C}}_{\mathrm{p},\mathrm{mean}})}^2}{\mathrm{n}}}$$

(12)

$${\mathrm{C}}_{\mathrm{p},\mathrm{peak}}=\min \left\{{\mathrm{C}}_{\mathrm{p},\mathrm{i}}\right\} ; \left(\sin \mathrm{gle} \mathrm{worst} \mathrm{minimum}\right)$$

(13)

$${\mathrm{Surface} \mathrm{avaraged} \mathrm{C}}_{\mathrm{P}}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{C}}_{\mathrm{P}}{\mathrm{A}}_{\mathrm{i}}}{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{A}}_{\mathrm{i}}}; \mathrm{for} \mathrm{mean}, \mathrm{rms}, \mathrm{and} \mathrm{peak}$$

(14)

where ${\mathrm{C}}_{\mathrm{p},\mathrm{i}}$ represents instantaneous external wind pressure, u_h denotes wind velocity at roof-mid height and ρ air density. A_i refers to the tributary area of a pressure tap and n is the total number of time steps).

Each model consists of four H/B ratios (0.25, 0.5, 0.75, and 1), three D/B ratios (1, 1.5, 2.5) and seven distinct wind directions (0°, 15°, 30°, 45°, 60°, 75°, 90°). Next, the roof pitch (α) of each model was altered eight times (5°, 10°, 14°, 18°, 22°, 27°, 30°, 45°). The last independent variable of the data set is surface, including walls and building roof (S1 to S6), marked in Figure 1. In addition, C_p,mean, C_p,rms, and C_p,peak are prediction variables.

Table 1. Descriptive statistics of the dataset.

Type	Variable	Details
Independent	Wind direction (θ)	0°, 15°, 30°, 45°, 60°, 75°, 90°
	Roof Pitch (α)	5°, 10°, 14°, 18°, 22°, 27°, 30°, 45°
	H/B	0.25, 0.5, 0.75, 1
	D/B	1, 1.5, 2.5
	S1	One-hot encoding is active. A value of “1” is used when a particular surface is referred whereas remaining surfaces hold “0”.
	S2
	S3
	S4
	S5
	S6
Dependant	Cp,mean	Ranges from −1.39 to 0.74
	Cp,rms	Ranges from 0.09 to 0.57
	Cp,peak [Single worst minimum]	Ranges from −4.91 to −0.13

provides a summary of the input and output variables of the present study. Since surface 1 to surface 6 is categorical, we used one-hot encoding. For occasions where an ordinary relationship does not exist, one-hot encoding is a better option compared to integer encoding. All independent and predicting variables were tabulated and 60% of data samples (2420 out of 4032 total samples) were fed into the training sequence while the remaining 40% is employed for the validation (out-of-bag data) process. All variables were provided to four tree-based algorithms through the sci-kit learn library in python [84].

In addition, hyperparameters are required to optimize all four models. All required hyperparameters of four tree-based models were chosen based on a grid search. Optimized model predictions were compared using performance indices. Subsequently, we followed the model explanatory process to elucidate the causality of predictions. Figure 2 summarizes the workflow of this study. The methodology shows the existing research gap in the wind engineering field. Therefore, the authors strongly believe the novelty-explainable ML- would advance the wind engineering research community.

6. Results and Discussion

6.1. Hyperparameter Optimization

The grid search method was used to optimize the hyperparameters for all four tree-based models. Grid search considers different combinations of parameters and evaluated their respective output to obtain optimum values.

Table 2. Optimized hyperparameters for tree-based ML models.

	Decision Tree		Extra Tree		XGBoost		LightGBM
	Hyperparameter	Value	Hyperparameter	Value	Hyperparameter	Value	Hyperparameter	Value
CP,mean	criterion	MSE	criterion	MSE	Maximum depth	4	Learning rate	0.1
	splitter	Best	Maximum depth	10	Gamma	0.0002	Maximum depth	4
	Maximum depth	10	Minimum samples leaf	2	Learning rate	0.3	Random state	5464
	Minimum samples leaf	2	Minimum sample split	2	Number of Estimators	50	Number of jobs	none
	Minimum sample split	2	Number of Estimators	50	Random state	154	Reg_Alpha	1 × 10−4
	Maximum Features	5	Bootstrap	FALSE	Reg_Alpha	0.0001
	Minimum impurity decrease	0	Minimum impurity decrease	0	Base score	0.5
	Random state	5464	Random state	5464
	CC alpha	0	Number of jobs	none
Cp,rms	criterion	MSE	criterion	MSE	Maximum depth	5	Learning rate	0.1
	splitter	Best	Maximum depth	10	Gamma	0.0001	Maximum depth	5
	Maximum depth	10	Minimum samples leaf	2	Learning rate	0.4	Random state	5464
	Minimum samples leaf	2	Minimum sample split	2	Number of Estimators	400	Number of jobs	none
	Minimum sample split	2	Number of Estimators	100	Random state	154	Reg_Alpha	1 × 10−4
	Maximum Features	5	Bootstrap	True	Reg_Alpha	0.0001
	Minimum impurity decrease	0	Minimum impurity decrease	0	Base score	0.5
	Random state	5464	Random state	4745
	CC alpha	0	Number of jobs	100
Cp,peak	criterion	MSE	criterion	MSE	Maximum depth	4	Learning rate	0.1
	splitter	Best	Maximum depth	10	Gamma	0.0001	Maximum depth	5
	Maximum depth	10	Minimum samples leaf	2	Learning rate	0.053	Random state	5464
	Minimum samples leaf	2	Minimum sample split	2	Number of Estimators	400	Number of jobs	none
	Minimum sample split	2	Number of Estimators	100	Random state	154	Reg_Alpha	1 × 10−4
	Maximum Features	5	Bootstrap	True	Reg_Alpha	0.0001
	Minimum impurity decrease	0	Minimum impurity decrease	0	Base score	0.5
	Random state	5464	Random state	4745
	CC alpha	0	Number of jobs	100

presents the optimized hyperparameters for each model. Their definitions are presented in Appendix A. Interestingly, tree-depth held a greater significance compared to the remaining hyperparameters. Figure 3 depicts how the accuracy of training and validation depends on tree-depth.

6.2. Training and Validation of Tree-Based Models

Figure 3 depicts the performance of tree-based regressors in terms of training and validation. Both XGBoost and LightGBM achieve an R² > 0.8 at a depth of 3, showing greater adaptability to wind pressure data. The Decision Tree regressor comprises enhanced predictions at depths between 5 and 10, though it is considered a weak learner compared to the remaining models. Both the Decision Tree and the Extra Tree slowly increase prediction accuracy with respect to remaining tree-based models. Compared to the training process of C_p,mean, Decision Tree, Extra Tree, and LightGBM decelerated training phase of C_p,rms, and C_p,peak as shown in Figure 3. However, the same performance was maintained by the XGBoost regressor throughout the entire training process. Despite different forms of pressure coefficients, all models exceed R² beyond 0.95 and become stalled between depths of 5 to 10. It is noteworthy that the stalled R² values beyond depths of 10 can lead to overfit the model.

6.3. Prediction of Surface-Averaged Pressure Coefficients

According to Figure 4, all models provide accurate predictions to the validation set of C_p,mean compared to wind tunnel data. XGBoost and Extra-Tree exhibit improved predictions with moderately higher R² values of 0.992 and 0.985, respectively. The Extra-Tree and XGBoost maintain the consistency of validation predictions for both negative and positive values within a 20% margin, most of the time. Slight inconsistencies can be observed for negative predictions obtained from the Decision Tree regressor. The accuracy of LightGBM is also satisfactory for C_p,mean predictions.

The coefficient C_p,rms represents turbulent fluctuations. C_p,rms is important, especially along perimeter regions where high turbulence is present. However, such localization was not feasible with the available data set due to the distinct pressure tap arrangement of each geometry configuration. Hence, for the present study, we had to employ (area-averaged) C_p,rms coefficient, which may not reflect localized effects. Nevertheless, the accuracy of validation predictions remains within a 20% error margin except for the Decision Tree regressor (see Figure 5). Both the XGBoost and LightGBM validation predictions are consistent, achieving relatively higher R² values.

For C_p,peak predictions, negative peaks were only considered as they induce large uplift forces on the external envelope [84]. Generally, the external pressure on roofs is more important than the pressure on walls as the roof is subjected to relatively larger negative pressure compared to walls. Especially negative pressure on the roof surface is critical to assess vulnerability for progressive failures [85]. Even with surface averaging, values closer to −5 (See Figure 6) have been obtained. Compared to mean and fluctuation predictions, peak pressure predictions (validation) have deviations beyond the 20% error limit for all tree-based models. In the case of the Decision Tree model, substantial deviations are visible for lower C_p,peak values, compared to wind tunnel data. Repeatedly, the XGBoost model showcased superior performance (R² = 0.955) with respect to the remaining models.

6.4. Performance Evaluation of Tree-Based Models

Figure 4, Figure 5 and Figure 6 provide insights into the applicability of tree-based models to predict wind pressure coefficients. However, models require performance analysis to explain the uncertainty associated with each model. The summary of model performance indices (validation predictions) is shown in

Table 3. Performance indices of optimized tree-based models.

Cp	Performance Indicators	Decision Tree	Extra Tree	LightGBM	XGBoost
Cp,mean	Correlation (R)	0.990	0.993	0.977	0.996
	MAE	0.049	0.043	0.051	0.033
	RMSE	0.067	0.055	0.07	0.043
Cp,rms	Correlation (R)	0.955	0.966	0.969	0.977
	MAE	0.018	0.016	0.015	0.013
	RMSE	0.023	0.020	0.019	0.017
Cp,peak	Correlation (R)	0.957	0.970	0.970	0.974
	MAE	0.177	0.150	0.149	0.143
	RMSE	0.246	0.206	0.205	0.192

.

Based on lower tree depth, XGBoost and LightGBM perform better than the remaining two models. In terms of validation predictions, XGBoost achieved the highest correlation. All models are adaptable to C_p,rms predictions as observed from lower MAE and RMSE values. Among four models, the Decision Tree showcased the lowest accuracy for C_p,rms, and C_p,peak whereas lightGBM showcased the lowest accuracy for C_p,mean predictions.

Bre et al. [33] obtained an R of 0.9995 for C_p,mean predictions of gable-roofed low-rise buildings using an ANN. According to Table 3, the same task is performed using tree-based ML models (R > 0.98) while expanding predictions to C_p,peak, and C_p,rms. In this study, we have separately provided training and validation accuracies because reliability is a measure in terms of the accuracy of training and validation (refer to Figure 7). For example, if training accuracy is considerably higher than validation, it leads to over-fitting. Lower accuracies of both imply under-fitting occasions. Therefore, obtaining similar accuracies in training and validation is more important (see Figure 3). Based upon R, RMSE, and MAE values, the XGBoost model was selected as the superior model and continued to the explanatory process.

7. Model Explanations

7.1. Model-Based (Intrinsic) Explanations

All tree-based algorithms used in this study are based on the Decision Tree structure. A simple Decision Tree is explainable without a post hoc agent. Figure 8 provides a Decision Tree regressor formed at a depth of three for the current study. X[number] denotes the number assigned to a variable in the selected order. (0—wind angle (θ); 1—D/B; 2—H/B; 3—Roof angle (α); 4—Surface 1 (S1); 5—Surface 2 (S2); 6—Surface 3 (S3); 7—Surface 4 (S4); 8—Surface 5 (S5); 9—Surface 6 (S6)). Value in the box refers to the mean value of the predictor variable of the samples passing through each box.

Splitting takes place at each node based on MSE. The selection criteria are followed by “IF-THEN” and “ELSE” statements. For instance, at the root node of the Decision Tree, variables are clustered based on whether it is surface 4 (X [7]) or not. After confirming value does not belong to surface 4, the tree decides wind direction (X [0]) should be examined. There it leads to initiate clustering depending on whether the θ < 37.5°. Subsequently, (θ < 37.5°) is clustered farther towards the left whereas the remaining will be clustered to the right. Interestingly, layer-wise splitting is performed by separating large deviations into a single group, gradually reducing MSE.

Though XGBoost, Extra-tree, and LightGBM are Decision Tree-based architectures, within those tree-based models, various methods such as bagging and boosting are implemented, which lead to perceive different outcomes. For example, XGBoost forms numerous Decision Trees at a particular point and conducts voting criteria to obtain a suitable one.

7.2. SHAP Explanations

As previously highlighted, a post hoc component is required to explain complex models. The authors used SHAP for this purpose. The explanatory process is divided into two stages. First, the global explanation is provided using SHAP explanations. Secondly, instance SHAP values are explained to compare the causality of predictions with respect to experimental behavior. Figure 9 depicts SHAP explanation on C_p,mean prediction of XGBoost.

The horizontal axis determines whether the impact is negative or positive. Feature values are denoted using red and blue color, whereas the former indicates higher feature values and the latter represents lower values. For example, wind angle contains several distinct values. Therefore, SHAP identifies values closer to 90° as higher feature values and values closer to 0° as lower feature values. Further, all surfaces are binary variables such that “1” (Higher feature value) means that the instance belongs to a particular surface and “0” (Lower feature value) indicates that the instance does not belong to the corresponding surface. SHAP identified that if instances belong to surface 4, there is a higher possibility to make a positive impact on the model whereas “not being surface 4” influences a low negative impact on the model. Generally, surface 3 and surface 4 experience positive C_p,mean values when it is facing a windward direction. Therefore, a considerable positive effect can be expected on the model output as identified by SHAP. Subsequently, concatenated blue-colored values explicate that there are more instances where a low negative impact occurs due to lower feature values.

When the wind angle (θ) is considered, the concatenated portion is observed towards the middle of the horizontal axis. That explains more instances exist where a neutral effect is observed regardless of feature values. Nevertheless, higher wind angles (closer to 90°) have influenced a moderately higher negative effect on model output. Fascinatingly, SHAP recognizes that higher roof pitch influences a positive effect on model output. According to SHAP explanation, surface 2, surface 3, surface 4, roof angle and wind angle have a substantial contribution to C_p,mean compared to the remaining variables.

A markedly different explanation was obtained for C_p,rms (See Figure 10). Surface 3 has become a crucial factor for model output. If a particular instance belongs to surface 3, it results in a positive impact on the model. Surface 2 has influenced a considerable positive (SHAP value > 0.125) effect on C_p,rms. Lower values of wind angle and H/B ratio cause a negative influence on the output. Surface 5 creates a mixed effect based on feature values, and that effect is more pronounced in roof angle and wind angle. However, concatenated regions indicate a neutral effect from wind angle and roof angle regardless of feature value. Overall, the effect of surface 6 was less notable on C_p,rms. Effects of H/B and D/B ratios on C_p,rms contradict the effect that appeared on C_p,mean.

Repeatedly, Surface 3 (S3) and Surface 4 (S4) provided a comparable effect on C_p,peak (See Figure 11). In addition, Surface 5 and Surface 6 (roof halves) show a similar effect on model output except for the fact that surface 5 can influence both positive and negative effects on C_p,peak. A notable difference was observed from the θ that influences a relatively higher negative effect on the ML model regardless of feature value. On the contrary, roof pitch (α) creates a dissimilar effect compared to θ, whereas higher feature values create a positive impact and lower features create a negative impact. H/B and D/B ratio creates a completely different impact on C_p,peak. Compared to the C_p,rms, the effect of surfaces 1 and 2 has been reversed. Less notable features observed in C_p,mean have become considerably important for the C_p,peak. The overall effect of surfaces 3 and 4 was similar for all forms of predictions. The effects of H/B and D/B were comparable for C_p,mean, and C_p,peak but completely reversed for C_p,rms. There exist instances in which the effect of wind direction and roof pitch appeared to be less dependent on feature values. However, we recognized that a completely different impact was observed from wind direction and roof pitch. The effect of roof surfaces becomes pronounced C_p,peak.

Heretofore, a generic overview of XGBoost models was described with the aid of SHAP explanations. Further, SHAP can provide a force plot picture based on each instance. That elucidates how each parameter forces the base value. The base value is defined as the average value observed during the training sequence. Red color features force the base value to be higher and blue color features force the lower side. The length of each segment is proportionate to its contribution (see Figure 12). SHAP can quantify the largest influential parameters at any given instance, assisting decision-making.

For example, we can consider three instances on surface 3, varying the only direction of the wind as 0°, 45°, and 90°. Figure 12 illustrates the SHAP force plot on these instances, considering C_p,mean. The base value tends to reduce when θ increases. For example, at θ = 0°, approaching wind directly attacks surface 3, where maximum positive pressure is obtained. Subsequently, positive pressure decreases for oblique wind directions as observed at θ = 45°. Thus, the maximum negative value is obtained at θ = 90° when surface 3 becomes a sidewall. From θ = 0° to θ = 90°, the effect of flow separation causes negative pressure to dominate on surface 3. Similar variation is observed based on the SHAP explanation where the effect of wind angle is positive (forcing towards higher values; Figure 12a) and gradually becomes negative (forcing towards lower values; Figure 12c). SHAP claims negative contribution is substantial at θ = 90° compared to the magnitude of contribution at θ = 0°. Moreover, SHAP has quantified the contribution of each parameter toward the instance value.

Figure 13 displays four instances of C_p,mean on surface 2 at θ = 90° (along wind direction for surface 2). More importantly, SHAP confirmed the effect of roof pitch as one of the influencing parameters in each instance. From α = 5° to α = 45°, the effect of roof pitch shifts from negative (forcing towards lower) to positive (forcing towards higher). From the wind engineering viewpoint, flat roofs induce large negative pressure due to the effect of flow separation along the upwind edge. When roof pitch increases, the effect of flow separation on the upwind half of the roof becomes less pronounced [85]. Further, at α = 45°, positive values dominate on the upwind half of the building roof, indicating flow reattachments.

Figure 14 and Figure 15 describe three instances of C_p,rms, and C_p,peak on surface 1 at θ = 0° (crosswind direction for surface 1), for three different roof pitches (α = 5°, 14°, 27°). SHAP identifies that both C_p,rms, and C_p,peak have increased due to increased roof pitch. Interestingly, wind tunnel results confirmed the same observations as a result of an increase in roof pitch. Except for roof pitch and H/B, the remaining parameters force the base value towards the lower side (Figure 15). C_p,rms are critical in zones where high turbulence is expected. Peak values are critical, especially near roof corners and perimeter zones. The overall explanations indicate that SHAP adheres to what is generally observed in the external pressure of the low-rise gable-roofed building.

8. Conclusions

Implementation of ML in wind engineering needs to advance the end-user’s trust in the predictions. In this study, we predicted surface-averaged pressure coefficients (mean, fluctuation, peak) of low-rise gable-roofed buildings, using tree-based ML architectures. The explanation method—SHAP—was used to elucidate the inner working and predictions of tree-based ML models. Following are the key conclusions of this study:

• Ensemble methods such as XGBoost and Extra tree are more accurate in estimating surface averaged pressure coefficients than a Decision Tree and LightGBM model. However, decision tree and extra-tree models require a deeper tree structure to achieve good accuracy. Despite the complexity at higher depths, the decision-tree structure is self-explainable. However, complex tree formations (ensemble method: XGBoost, Extra Tree, LightgGBM) require a post hoc explanation method.
• All tree-based models (Decision Tree, Extra tree, XGBoost, LightGBM) accurately predict surface-averaged wind pressure coefficients (C_p,mean, C_p,rms, C_p,peak). For example, tree-based models reproduce surface averaged mean, fluctuating, and peak pressure coefficients (R > 0.955). XGBoost model achieved the best performance (R > 0.974).
• SHAP explanations convinced predictions to adhere to the elementary flow physics of wind engineering. This provides causality of predictions, the importance of features, and interaction between the features to assist the decision-making process. The knowledge offered by SHAP is highly imperative to optimize the features at the design stage. Further, combining a post hoc explanation with ML provides confidence to its end-user on “how a particular instance is predicted”.

9. Limitations of the Study

• According to the obtained TPU data set, the pressure tap configuration is not uniform for each geometry configuration. Therefore, investigating point pressure predictions is difficult. Further, the data set has a limited number of features. Hence, we suggest a comprehensive study to examine the performance of explainable ML, addressing these drawbacks. Adding more parameters would assist in understanding complex behaviors of external wind pressure around low-rise buildings. For example, the external pressure distribution strongly depends on wind velocity and turbulence intensity [86,87]. Therefore, the authors suggest future studies, incorporating these two parameters.
• We used SHAP explanations for the model interpretations. However, there are many explanatory models available to perform the same task. Each model might result in a unique feature importance value. For example, Moradi and Samweld [62] explained the difference between LIME and SHAP on how those models explain an instance. Therefore, a separate study can be conducted using several interpretable (post hoc) models to evaluate the explanations. In addition, we recommend comparing intrinsic explanations to investigate the effect of model building and the training process of ML models.
• The present study chooses tree-based ordinary and ensemble methods to predict wind pressure coefficients. As highlighted in the introduction section, many authors have employed sophisticated models (Neural Network Architectures: ANN, DNN) to predict wind pressure characteristics. Given their opinion, we suggest combining interpretation methods with such advanced methods to examine the difference between different ML models.