Condition Assessment of Grouped Cable Forces of Cable-Stayed Bridge Using Deflection Data
Abstract
:1. Introduction
2. Methodology for Cable Force Assessment
2.1. Relationship between Cable Force and Girder Deflection
- (1)
- Assuming that the pylon’s bending stiffness is infinite, the cable’s elongation is the only factor contributing to the girder’s deflection, as shown in Figure 2a. The lateral stiffness of the girder is much stronger than the vertical stiffness, so its lateral displacement can be ignored.
- (2)
- Assuming that the axial stiffness of the cable is infinite, the girder’s deflection is exclusively caused by the pylon’s bending, as shown in Figure 2b.

2.2. Condition Assessment Method of Grouped Cable
2.2.1. Evaluation Standard of Single Cable
2.2.2. Assessment of Grouped Cable
3. Case Study
3.1. Engineering Background
3.2. Verification of the Relationship between Cable Force and Deflection
3.3. Assessment Example
4. Conclusions
- (1)
- According to the geometric relationship of the deformation in cable-stayed bridge, a simplified equation between the variation in cable forces and the girder deflection was built. A practical case study validated the correctness of the proposed theoretical equation.
- (2)
- The threshold value of cable force change rate for a single cable can be determined by a simplified equation between the cable force and girder deflection and the deflection limit in the specification. In this case, the threshold of a long cable is 30%. On this basis, the evaluation standard of a single cable force of piecewise linear mode was obtained according to the specifications.
- (3)
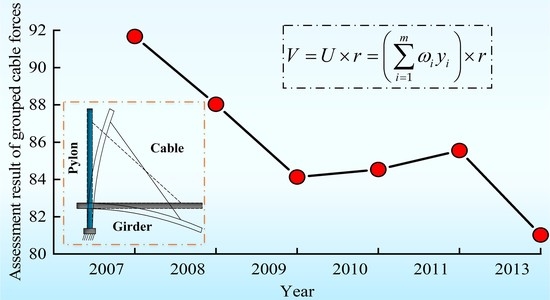
- A condition assessment method of grouped cable forces was established based on the variable weight synthesis method and gray correlation degree theory, which considers the uniform and non-uniform changes in cable force. The 6-year evaluation results of grouped cables of a real bridge show that the cable forces are generally decreasing year by year, and it also reflects the development of other component defects from the side.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Cable cross-sectional area |
| Eeq | Equivalent elastic modulus of cables |
| Ec | Elastic modulus of cable |
| Ep | Pylon elastic modulus |
| hi | Height of the ith cable from the deck |
| Ip | Area moment of inertia of pylon |
| Lc | Cable length |
| l | Length of the cable horizontal projection |
| m | The total number of cable force monitoring points |
| n | Number of pairs of cables anchored at each pylon |
| r | Non-uniform variation coefficient |
| T | Cable force |
| U | Score for uniform variation |
| V | Grouped cable assessment value |
| xk(0) | The kth initial monitoring cable force |
| xk | The kth current monitoring cable force |
| x | Cable force variation rate |
| yi | Score value of the ith monitoring point |
| α | Horizontal angle between cable and deck |
| w0 | Cable weight per unit length |
| ωi | Weight of the ith monitoring point |
| ∆T | Cable force variation |
| ∆Ti | Variation in cable force of the ith cable on the river side |
| ∆T’i | Variation in cable force of the ith cable on the bank |
| ∆u1 | Deflection of main girder caused by cable extension |
| ∆u2 | Deflection of main girder caused by pylon’s bending |
| ∆u | Deflection of main girder (∆u1 + ∆u2) |
| ∆v | Longitudinal displacement of the anchor point |
References
- Gimsing, N.J.; Georgakis, C.T. Cable Supported Bridges: Concept and Design; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Jin, D.; Liu, X.; Wang, B.; Huang, Q. Main girder deflection variations in cable-stayed bridge with temperature over various time scales. Math. Probl. Eng. 2020, 2020, 4316921. [Google Scholar] [CrossRef]
- Guo, J.; Gu, Y.; Wu, W.; Chu, S.; Dang, X. Seismic fragility assessment of cable-stayed bridges crossing fault rupture zones. Buildings 2022, 12, 1045. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, T.; Chai, S. Probabilistic fatigue life prediction of bridge cables based on multiscaling and mesoscopic fracture mechanics. Appl. Sci. 2016, 6, 99. [Google Scholar] [CrossRef]
- Ma, Y.; Peng, A.; Wang, L.; Dai, L.; Zhang, J. Structural performance degradation of cable-stayed bridges subjected to cable damage: Model test and theoretical prediction. Struct. Infrastruct. Eng. 2021, 1–17. [Google Scholar] [CrossRef]
- Yao, S.; Peng, B.; Wang, L.; Chen, H. Structural Performance and Reasonable Cross-Ratio of Cross-Cable Multi-Tower Cable-Stayed Bridges. Buildings 2022, 12, 764. [Google Scholar] [CrossRef]
- Soe, T.T.T. Evaluation of cable force changes effects on cable stayed bridge. KSCE J. Civ. Eng. 2020, 6, 2159–2174. [Google Scholar] [CrossRef]
- Civera, M.; Calamai, G.; Fragonara, L.Z. System identification via fast relaxed vector fitting for the structural health monitoring of masonry bridges. Structures 2021, 30, 277–293. [Google Scholar] [CrossRef]
- Li, H.; Ou, J. The state of the art in structural health monitoring of cable-stayed bridges. J. Civ. Struct. 2016, 6, 43–67. [Google Scholar] [CrossRef]
- Wang, Z.L.; Yang, J.P.; Shi, K.; Xu, H.; Qiu, F.Q.; Yang, Y.B. Recent advances in researches on vehicle scanning method for bridges. Int. J. Struct. Stab. Dyn. 2022, 22, 2230005. [Google Scholar] [CrossRef]
- JTG/T H21-2011; Standards for Technical Condition Evaluation of Highway Bridges. Ministry of Transport of the People’s Republic of China: Beijing, China, 2011.
- Fan, Z.Y.; Huang, Q.; Ren, Y.; Zhu, Z.Y.; Xu, X. A cointegration approach for cable anomaly warning based on structural health monitoring data: An application to cable-stayed bridges. Adv. Struct. Eng. 2020, 23, 2789–2802. [Google Scholar] [CrossRef]
- Cho, H.N.; Choi, Y.M.; Lee, S.C.; Kang, K.K.; Choi, M.Y. Critical threshold value for monitoring & management of cable tension force in cable-stayed bridge. Key Eng. Mater. 2004, 270–273, 1977–1982. [Google Scholar]
- Liang, Y.; Li, D.; Song, G.; Feng, Q. Frequency Co-integration-based damage detection for bridges under the influence of environmental temperature variation. Measurement 2018, 125, 163–175. [Google Scholar] [CrossRef]
- Chen, C.C.; Wu, W.H.; Liu, C.Y.; Lai, G. Damage detection of a cable-stayed bridge based on the variation of stay cable forces eliminating environmental temperature effects. Smart Struct. Syst. 2016, 17, 859–880. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, X.L.; Huang, Q. The long-term trend analysis and assessment of the cable forces due to dead load in cable-stayed bridges. J. Harbin. Inst. Technol. 2015, 47, 103–108. [Google Scholar]
- Huang, Y.; Wang, Y.; Fu, J.; Liu, A.; Gao, W. Measurement of the real-time deflection of cable-stayed bridge based on cable tension variations. Measurement 2018, 119, 218–228. [Google Scholar] [CrossRef]
- Cong, L. Research on safety assessment method for bridge structure based on variable weight synthesis method. Perspect. Sci. 2016, 7, 200–203. [Google Scholar] [CrossRef]
- Sun, S.; Liang, L.; Li, M. Condition assessment of stay cables via cloud evidence fusion. KSCE J. Civ. Eng. 2021, 25, 866–878. [Google Scholar] [CrossRef]
- Xu, X.; Huang, Q.; Ren, Y.; Sun, H.B. Condition assessment of suspension bridges using local variable weight and normal cloud model. KSCE J. Civ. Eng. 2018, 22, 4064–4072. [Google Scholar] [CrossRef]
- Dan, D.H.; Zhao, Y.M.; Yang, T.; Yan, X.F. Health condition evaluation of cable-stayed bridge driven by dissimilarity measures of grouped cable forces. Int. J. Distrib. Sens. Netw. 2013, 9, 818967. [Google Scholar] [CrossRef]
- Wang, P.H.; Lin, H.T.; Tang, T.Y. Study on nonlinear analysis of a highly redundant cable-stayed bridge. Comput. Struct. 2002, 80, 165–182. [Google Scholar] [CrossRef]
- Xiang, H.F. Advanced Theory of Bridge Structures, 2nd ed.; China Communications Press: Beijing, China, 2013. [Google Scholar]
- Wen, Y.; Zhou, Z. Qualification of the Ernst formula for modeling the sag effect of super-long stay cables in the long-span railway cable-stayed bridges. Structures 2022, 45, 99–109. [Google Scholar] [CrossRef]
- JTG/T 3365-01-2020; Specifications for Design of Highway Cable-Stayed Bridge. Ministry of Transport of the People’s Republic of China: Beijing, China, 2020.
- Xiong, W.; Tu, X.; Xiao, R. Condition assessment of stay cable forces based on variation and trend coefficients. J. Tongji Univ. Nat. Sci. 2011, 39, 1575–1580. [Google Scholar]
- Lan, H.; Shi, J.J. Degree of grey incidence and variable weight synthesizing applied in bridge assessment. J. Tongji Univ. Nat. Sci. 2001, 29, 50–54. [Google Scholar]
- Fu, Z.; Ji, B.; Yang, M.; Sun, H.; Maeno, H. Cable replacement method for cable-stayed bridges based on sensitivity analysis. J. Perform. Constr. Facil. 2015, 29, 04014085. [Google Scholar] [CrossRef]
- Mehrabi, A.B. Performance of cable-stayed bridges: Evaluation methods, observations, and rehabilitation case. J. Perform. Constr. Facil. 2016, 30, C4014007. [Google Scholar] [CrossRef]










| Technical Condition Level | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|
| Technical condition score | [95, 100] | [80, 95) | [60, 80) | [40, 60) | [0, 40) |
| Commonly employed feasible actions | Daily maintenance or preventive maintenance | Preventive maintenance or repair maintenance | Repair maintenance or rehabilitation | Rehabilitation or repair maintenance | Rehabilitation or replacement |
| Cable Number | NJ21 | NA21 | NJ20 | NA20 | NJ19 | NA19 | NJ18 | NA18 |
|---|---|---|---|---|---|---|---|---|
| Cable force variation rate | 22% | 26% | 31% | 30% | 33% | 31% | 32% | 33% |
| Date | Uniform Assessment Score | Non-Uniform Coefficient | Assessment Score of Grouped Cable | Condition Level |
|---|---|---|---|---|
| 2007.03 | 93.69 | 0.982 | 91.67 | 2 |
| 2008.04 | 90.06 | 0.982 | 88.03 | 2 |
| 2009.04 | 86.91 | 0.974 | 84.13 | 2 |
| 2010.10 | 87.01 | 0.973 | 84.53 | 2 |
| 2011.11 | 86.53 | 0.986 | 85.55 | 2 |
| 2013.12 | 82.67 | 0.977 | 81.02 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Yi, X.; Wang, B.; Liu, Y. Condition Assessment of Grouped Cable Forces of Cable-Stayed Bridge Using Deflection Data. Buildings 2023, 13, 472. https://doi.org/10.3390/buildings13020472
Liu X, Yi X, Wang B, Liu Y. Condition Assessment of Grouped Cable Forces of Cable-Stayed Bridge Using Deflection Data. Buildings. 2023; 13(2):472. https://doi.org/10.3390/buildings13020472
Chicago/Turabian StyleLiu, Xiaoling, Xiyan Yi, Bing Wang, and Ying Liu. 2023. "Condition Assessment of Grouped Cable Forces of Cable-Stayed Bridge Using Deflection Data" Buildings 13, no. 2: 472. https://doi.org/10.3390/buildings13020472
APA StyleLiu, X., Yi, X., Wang, B., & Liu, Y. (2023). Condition Assessment of Grouped Cable Forces of Cable-Stayed Bridge Using Deflection Data. Buildings, 13(2), 472. https://doi.org/10.3390/buildings13020472