Experimental and Numerical Investigation of the Behavior of Steel Beams Strengthened by Bolted Hybrid FRP Composites
Abstract
:1. Introduction
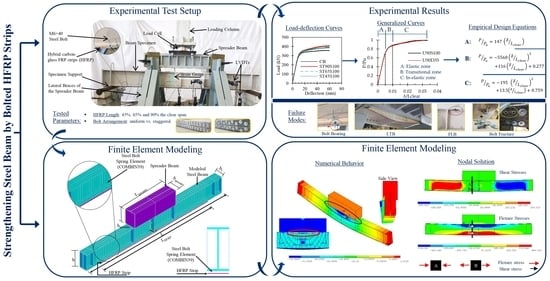
2. Experimental Study
2.1. Material Properties
2.2. Methodology and Test Matrix
2.3. Test Set-Up
3. Experimental Results
3.1. Failure Modes
3.2. Effect of HFRP Length
3.2.1. Load-Deflection Curves
3.2.2. Deflection Profiles
3.2.3. Strain Measurements
3.3. Effect of Bolt Arrangement
3.3.1. Load-Deflection Curves
3.3.2. Strain Measurements
3.4. Development of Empirical Load-Deflection Equations
4. Finite Element Modeling
4.1. Model Development
4.1.1. Description and Geometry
4.1.2. Material Modeling
4.1.3. Boundary Conditions
4.2. Model Verification
4.3. Parametric Finite Element Study
4.3.1. HFRP Thickness and Bolt Spacing
4.3.2. Steel Grade
4.3.3. Loading Scheme
4.3.4. Beam Length
5. Conclusions
- Steel beams strengthened by bolted HFRP strips showed ductile behavior while experiencing steel yielding, bearing between the bolts and the HFRP, lateral torsional buckling, and flange local buckling. However, a sufficient number of bolts should be provided to avoid the possibility of shear fracture in the bolts.
- The proposed fastening technique resulted in significant enhancements in the flexural performance of the strengthened beams, with 15.1% and 22.2% increases in the yield and ultimate flexural capacities compared to the control beam.
- Better utilization of the HFRP strength was achieved by utilizing long HFRP strips.
- Increasing the length of the HFRP strip from 45% to 90% of the beam span slightly improved the yield and ultimate flexural capacities of the system. However, it significantly enhanced the ductility of the system and provided better utilization of the bolted HFRP. A 51.2% reduction in the mid-span deflection was attained by increasing the length of the double HFRP strips from 45% to 90% of the beam span.
- The arrangement of the steel bolts did not show a considerable effect on the yield load, ultimate load, ductility, HFRP utilization, and strain compatibility of the bolted components.
- The plotted strain profiles proved the effectiveness of the fastening technique in reducing the strains at the bottom steel flange of the strengthened beams. Better strain compatibility and lower slippage were attained by increasing the length of the bolted HFRP strip. Meanwhile, the flexural strains along the bolted HFRP strips followed the distribution of the bending moment along the strengthened beams.
- Increasing the HFRP thickness without maintaining a proper number of bolts risked the ductility of the system and reduced its ultimate capacities due to the shear fracture of the bolts. Meanwhile, providing a sufficient number of bolts by reducing the bolt spacing enhanced the performance of the strengthened beams.
- Applying the fastening technique to beams made of A36 steel showed 11.4% and 34.5% improvement in the yield and ultimate loads compared to the control beam, respectively. The study recommends reducing the spacing between the bolts while strengthening the A36 steel beams to avoid shear fracture of the bolts.
- The beams subjected to three-point loading showed lower yield and ultimate load-carrying capacity than those subjected to four-point loading. This is attributed to the high shear stresses induced in the three-point loading conditions and, consequently, the high combined stresses induced in the beam’s section.
- The numerical study proved the effectiveness of the fastening technique in enhancing the performance of the strengthened beams regardless of the beam length. Strengthening a steel beam with a span of 3600 mm using four HFRP strips with 35 mm spaced steel bolts showed a 27.5% improvement in the ultimate load compared to the control beam.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zeng, J.-J.; Gao, W.-Y.; Liu, F. Interfacial behavior and debonding failures of full-scale CFRP-strengthened H-section steel beams. Compos. Struct. 2018, 201, 540–552. [Google Scholar] [CrossRef]
- Teng, J.G.; Yu, T.; Fernando, D. Strengthening of steel structures with fiber-reinforced polymer composites. J. Constr. Steel Res. 2012, 78, 131–143. [Google Scholar] [CrossRef]
- Tafsirojjaman, T.; Ur Rahman Dogar, A.; Liu, Y.; Manalo, A.; Thambiratnam, D.P. Performance and design of steel structures reinforced with FRP composites: A state-of-the-art review. Eng. Fail. Anal. 2022, 138, 106371. [Google Scholar] [CrossRef]
- Bastani, A.; Das, S.; Kenno, S. Rehabilitation of thin walled steel beams using CFRP fabric. Thin-Walled Struct. 2019, 143, 106215. [Google Scholar] [CrossRef]
- Hussein, L.F.; Abbas, F.S.; Al-Balhawi, A.; AL-Ridha, A.S.D.; Hussein, H.H. Investigating the elastic and plastic behavior of I-steel beams by using carbon fiber laminates. Mater. Today Proc. 2021, 56, 2714–2720. [Google Scholar] [CrossRef]
- Borrie, D.; Al-Saadi, S.; Zhao, X.-L.; Raman, R.K.S.; Bai, Y. Bonded CFRP/Steel Systems, Remedies of Bond Degradation and Behaviour of CFRP Repaired Steel: An Overview. Polymers 2021, 13, 1533. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.; Wu, G.; Wang, H.; Su, Z.; He, X. Experimental study on the bond behavior of CFRP-steel interfaces under quasi-static cyclic loading. Thin-Walled Struct. 2019, 140, 426–437. [Google Scholar] [CrossRef]
- Hu, B.; Li, Y.; Jiang, Y.-T.; Tang, H.-Z. Bond behavior of hybrid FRP-to-steel joints. Compos. Struct. 2020, 237, 111936. [Google Scholar] [CrossRef]
- Wang, Z.; Li, C.; Sui, L.; Xian, G. Effects of adhesive property and thickness on the bond performance between carbon fiber reinforced polymer laminate and steel. Thin-Walled Struct. 2021, 158, 107176. [Google Scholar] [CrossRef]
- Katrizadeh, E.; Narmashiri, K. Experimental study on failure modes of MF-CFRP strengthened steel beams. J. Constr. Steel Res. 2019, 158, 120–129. [Google Scholar] [CrossRef]
- Kumaraguru, S.; Alagusundaramoorthy, P. Flexural strengthening of steel beams using pultruded CFRP composite sheets with anchorage mechanisms. Structures 2021, 33, 1414–1427. [Google Scholar] [CrossRef]
- Al-Ridha, A.S.D.; Hameed, Q.K.; Atshan, A.F.; Abbood, A.A.; Dheyab, L.S. Evaluation of Strengthening Steel Beams Using the Technique of Carbon Fiber Confinement by a Steel Plate (CFCSP). Adv. Civ. Eng. Mater. 2020, 9, 53–66. [Google Scholar] [CrossRef]
- Esmaeeli, E.; Shadan, P. Effectiveness of Fan Anchors in Preventing Debonding in FRP-Strengthened Steel Members. Int. J. Steel Struct. 2022, 23, 96–119. [Google Scholar] [CrossRef]
- Siwowski, T.W.; Siwowska, P. Experimental study on CFRP-strengthened steel beams. Compos. Part B Eng. 2018, 149, 12–21. [Google Scholar] [CrossRef]
- Siwowski, T.; Piątek, B.; Siwowska, P.; Wiater, A. Development and implementation of CFRP post-tensioning system for bridge strengthening. Eng. Struct. 2020, 207, 110266. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, J.; Zhang, S.; Chastre, C.; Biscaia, H. Effect of mechanical anchorage on the bond performance of double overlapped CFRP-to-steel joints. Compos. Struct. 2021, 267, 113902. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Deng, J.; Jia, Y. Experimental study on the flexural behaviour of notched steel beams strengthened by prestressed CFRP plate with an end plate anchorage system. Eng. Struct. 2018, 171, 29–39. [Google Scholar] [CrossRef]
- Deng, J.; Fei, Z.; Li, J.; Li, H. Fatigue behaviour of notched steel beams strengthened by a self-prestressing SMA/CFRP composite. Eng. Struct. 2023, 274, 115077. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, Q.; Wu, Y.; Zhu, Y.; Wang, H. A theoretical and experimental study on the pre-tensioning and anchorage of composite materials based on shape memory alloys. Case Stud. Constr. Mater. 2023, 18, e01599. [Google Scholar] [CrossRef]
- Ghafoori, E.; Motavalli, M. Innovative CFRP-Prestressing System for Strengthening Metallic Structures. J. Compos. Constr. 2015, 19, 04015006. [Google Scholar] [CrossRef]
- Kianmofrad, F.; Ghafoori, E.; Elyasi, M.; Motavalli, M.; Rahimian, M. Strengthening of metallic beams with different types of pre-stressed unbonded retrofit systems. Compos. Struct. 2017, 159, 81–95. [Google Scholar] [CrossRef]
- Hosseini, A.; Ghafoori, E.; Motavalli, M.; Nussbaumer, A.; Zhao, X.L.; Al-Mahaidi, R. Flat pre-stressed unbonded retrofit system for strengthening of existing metallic I-Girders. Compos. Part B Eng. 2018, 155, 156–172. [Google Scholar] [CrossRef]
- Hai, N.D.; Mutsuyoshi, H. Structural behavior of double-lap joints of steel splice plates bolted/bonded to pultruded hybrid CFRP/GFRP laminates. Constr. Build. Mater. 2012, 30, 347–359. [Google Scholar] [CrossRef]
- Sweedan, A.M.I.; El-Sawy, K.M.; Alhadid, M.M.A. Interfacial behavior of mechanically anchored FRP laminates for strengthening steel beams. J. Constr. Steel Res. 2013, 80, 332–345. [Google Scholar] [CrossRef]
- Yun, J.-H.; Choi, J.-H.; Kweon, J.-H. A study on the strength improvement of the multi-bolted joint. Compos. Struct. 2014, 108, 409–416. [Google Scholar] [CrossRef]
- El-Sisi, A.E.-D.; Sallam, H.E.-D.; Salim, H.A.; El-Husseiny, O.M. Structural behavior of hybrid CFRP/steel bolted staggered joints. Constr. Build. Mater. 2018, 190, 1192–1207. [Google Scholar] [CrossRef]
- Abou El-Hamd, O.R.; Sweedan, A.M.I.; El-Sawy, K.M. Experimental and numerical study of the parameters controlling the behavior of double-lap connections of steel plates bolted to hybrid FRP strips. Thin-Walled Struct. 2018, 125, 140–151. [Google Scholar] [CrossRef]
- Liu, K.; Liu, Y.; Sabbrojjaman, M.; Tafsirojjaman, T. Effect of bolt size on the bearing strength of bolt-connected orthotropic CFRP laminate. Polymer Test. 2023, 118, 107894. [Google Scholar] [CrossRef]
- El-Sisi, A.E.-D.A.; El-Emam, H.M.; Salim, H.A.; Sallam, H.E.-D.M. Deformation and load transfer analysis of staggered composite-steel lap joints subjected to progressive damage. Eng. Struct. 2020, 215, 110690. [Google Scholar] [CrossRef]
- Jiang, Z.; Wan, S.; Fang, Z.; Song, A. Static and fatigue behaviours of a bolted GFRP/steel double lap joint. Thin-Walled Struct. 2020, 158, 107170. [Google Scholar] [CrossRef]
- Sweedan, A.M.I.; Alhadid, M.M.A.; El-Sawy, K.M. Experimental study of the flexural response of steel beams strengthened with anchored hybrid composites. Thin-Walled Struct. 2016, 99, 1–11. [Google Scholar] [CrossRef]
- Sweedan, A.M.I.; Rojob, H.N.; El-Sawy, K.M. Mechanically-fastened hybrid composites for flexural strengthening of steel beams. Thin-Walled Struct. 2014, 85, 250–261. [Google Scholar] [CrossRef]
- Sweedan, A.M.I.; Rojob, H.N.; El-Sawy, K.M. Analytical and numerical study of the serviceability performance of partial composite steel-FRP beams. Int. J. Struct. Integr. 2018, 9, 625–645. [Google Scholar] [CrossRef]
- About El-Hamd, O.R.; Sweedan, A.M.I.; El-Ariss, B. Flexural Performance of Steel Beams Strengthened by Fastened Hybrid FRP Strips Utilizing Staggered Steel Bolts. Buildings 2022, 12, 2150. [Google Scholar] [CrossRef]
- ASTM Standard A370-21; Standard Test Methods and Definitions for Mechanical Testing of Steel Products. American Society of Testing Materials (ASTM) Standards: West Conshohocken, PA, USA, 2021.
- Strongwell Manufacturing Plants. SAFSTRIP: Fiber Reinforced Strengthening Strip; Strongwell: Chatfield, MN, USA, 2020. [Google Scholar]
- DIN EN ISO 4017; Fasteners—Hexagon Head Screws—Product Grades A and B. DIN-Adopted European-Adopted ISO Standards. Deutsches Institut fur Normung (DIN) Standards: Berlin, Germany, 2014.
- Youssef, M.A. Analytical prediction of the linear and nonlinear behaviour of steel beams rehabilitated using FRP sheets. Eng. Struct. 2006, 28, 903–911. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Jumaat, M.; Sulong, N.H.R.; Qeshta, I.M.I.; Narmashiri, K. Effects of Lateral Bracing and Stiffeners on the CFRP Failure of Strengthened Steel Beams. IOP Conf. Ser. Mater. Sci. Eng. 2017, 210, 12021. [Google Scholar] [CrossRef] [Green Version]
- Peiris, A.; Harik, I. Steel beam strengthening with UHM CFRP strip panels. Eng. Struct. 2021, 226, 111395. [Google Scholar] [CrossRef]
- El Damatty, A.A.; Abushagur, M.; Youssef, M.A. Experimental and analytical investigation of steel beams rehabilitated using GFRP sheets. Steel Compos. Struct. 2003, 3, 421–438. [Google Scholar] [CrossRef]
- Ansys®. Mechanical APDL; Help System; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Salmon, C.G.; Johnson, J.E.; Malhas, F.A. Steel Structures, Design and Behavior, Emphasizing Load and Resistance Factor Design, 5th ed.; Pearson Prentice Hall Publishers: Hoboken, NJ, USA, 2009. [Google Scholar]
- Foster, A.S.J.; Gardner, L.; Wang, Y. Practical strain-hardening material properties for use in deformation-based structural steel design. Thin-Walled Struct. 2015, 92, 115–129. [Google Scholar] [CrossRef]
- Kachlakev, D. Strengthening Bridges Using Composite Materials; Oregon Department of Transportation Research Unit: Salem, OR, USA, 1998. [Google Scholar] [CrossRef]
- Kachlakev, D.I.; McCurry, D., Jr. Simulated Full Scale Testing of Reinforced Concrete Beams Strengthened with FRP Composites: Experimental Results and Design Model Verification; Oregon Department of Transportation: Salem, OR, USA, 2000. [Google Scholar]
- ASTM Standard A36/A36M; Standard Specification for Carbon Structural Steel. American Society of Testing Materials (ASTM) Standards: West Conshohocken, PA, USA, 2019.
- Daniel, I.M.; Abot, J.L. Fabrication, testing and analysis of composite sandwich beams. Compos. Sci. Technol. 2000, 60, 2455–2463. [Google Scholar] [CrossRef]
- Bencardino, F. Mechanical Parameters and Post-Cracking Behaviour of HPFRC According to Three-Point and Four-Point Bending Test. Adv. Civ. Eng. 2013, 2013, 179712. [Google Scholar] [CrossRef] [Green Version]
- Al-Abtah, F.G.; Mahdi, E.; Gowid, S. The use of composite to eliminate the effect of welding on the bending behavior of metallic pipes. Compos. Struct. 2020, 235, 111793. [Google Scholar] [CrossRef]
- McCormac, J.C. Structural Steel Design, 4th ed.; Pearson Prentice Hall: Hoboken, NJ, USA, 2008. [Google Scholar]















































| Specimen Designation | Bolt Arrangement | No. of Replicates | HFRP Length (LHFRP) (mm) | HFRP Thickness (mm) | Bolt Spacing (S) (mm) | Number of M6 Bolts |
|---|---|---|---|---|---|---|
| CB | - | 2 | - | - | - | - |
| U90S100 | Uniform | 2 | 1620 | 3.175 | 100 | 32 |
| U65S100 | Uniform | 2 | 1170 | 3.175 | 100 | 24 |
| U45S100 | Uniform | 2 | 810 | 3.175 | 100 | 16 |
| U90D35 | Uniform | 2 | 1620 | 6.350 | 35 | 96 |
| U65D35 | Uniform | 2 | 1170 | 6.350 | 35 | 72 |
| U45D35 | Uniform | 2 | 810 | 6.350 | 35 | 48 |
| ST90S100 | Staggered | 2 | 1620 | 3.175 | 100 | 32 |
| ST65S100 | Staggered | 2 | 1170 | 3.175 | 100 | 24 |
| ST45S100 | Staggered | 2 | 810 | 3.175 | 100 | 16 |
| ST90D35 | Staggered | 2 | 1620 | 6.350 | 35 | 96 |
| Specimen Designation | Average My (kN.m) | Average Mu (kN.m) | % Increase My *a | % Increase Mu *a | Failure Modes |
|---|---|---|---|---|---|
| CB | 78.24 | 107.40 | - | - | SY *b, LTB *c, FLB *d |
| U90S100 | 84.94 | 120.11 | 8.6 | 11.8 | BR *e, SY, LTB, FLB |
| U65S100 | 82.75 | 119.79 | 5.8 | 11.5 | BR, SY, LTB, FLB |
| U45S100 | 82.04 | 117.75 | 4.9 | 9.6 | BR, SY, LTB, FLB |
| U90D35 | 90.03 | 127.61 | 15.1 | 18.8 | BR, SY, LTB, FLB |
| U65D35 | 86.61 | 123.56 | 10.7 | 15.0 | BR, SY, LTB, FLB |
| U45D35 | 86.31 | 116.49 | 10.3 | 8.5 | BR, SY, BSF *f |
| ST90S100 | 84.89 | 122.68 | 8.5 | 14.2 | BR, SY, LTB, FLB |
| ST65S100 | 84.14 | 118.78 | 7.5 | 10.6 | BR, SY, LTB, FLB |
| ST45S100 | 82.32 | 116.53 | 5.2 | 8.5 | BR, SY, LTB, FLB |
| ST90D35 | 87.83 | 131.26 | 12.3 | 22.2 | BR, SY, LTB, FLB |
| Specimen Designation | εHFRP at Mid-Segment (με) | UσHFRP at Mid-Segment (%) | εHFRP at Edge-Segment (με) | UσHFRP at Edge-Segment (%) |
|---|---|---|---|---|
| U90S100 | 1716 | 12.5 | 980 | 7.2 |
| U65S100 | 1340 | 9.8 | 598 | 4.4 |
| U45S100 | 815 | 5.9 | 160 | 1.2 |
| U90D35 | 2154 | 15.7 | 1576 | 11.5 |
| U65D35 | 2148 | 15.7 | 1239 | 9.0 |
| U45D35 | 1192 | 8.7 | 179 | 1.3 |
| ST90S100 | 1899 | 13.9 | 1348 | 9.8 |
| ST65S100 | 1300 | 9.5 | 510 | 3.7 |
| ST45S100 | 665 | 4.9 | 9 | 0.1 |
| ST90D35 | 2376 | 17.3 | 1647 | 12.0 |
| Specimen Designation | Pu,EXP *a (kN) | Pu,EMP *b (kN) | Error (%) |
|---|---|---|---|
| U90S100 | 400.38 | 407.79 | 1.9 |
| U65S100 | 399.31 | 398.77 | 0.1 |
| U45S100 | 392.5 | 393.54 | 0.3 |
| U90D35 | 425.37 | 425.62 | 0.1 |
| U65D35 | 411.86 | 416.51 | 1.1 |
| U45D35 | 388.31 | 410.52 | 5.7 |
| ST90S100 | 408.92 | 407.79 | 0.3 |
| ST65S100 | 395.93 | 398.77 | 0.7 |
| ST45S100 | 388.44 | 393.54 | 1.3 |
| ST90D35 | 437.52 | 425.62 | 2.7 |
| Specimen Designation | Yield Load (kN) | Ultimate Load (kN) | ||||
|---|---|---|---|---|---|---|
| Py,EXP *a (kN) | Py,FE *b (kN) | ∆Py (%) | Pu,EXP *a (kN) | Pu,FE *b (kN) | ∆Pu (%) | |
| CB | 260.79 | 258.86 | 0.74 | 358.01 | 346.45 | 3.23 |
| U90S100 | 283.15 | 277.56 | 1.97 | 400.38 | 390.54 | 2.46 |
| U65S100 | 275.84 | 276.11 | 0.10 | 399.31 | 381.91 | 4.36 |
| U45S100 | 273.47 | 274.85 | 0.50 | 392.50 | 358.46 | 8.67 |
| U90D35 | 300.10 | 296.36 | 1.25 | 425.37 | 420.52 | 1.14 |
| U65D35 | 288.71 | 285.30 | 1.18 | 411.86 | 412.15 | 0.07 |
| U45D35 | 287.71 | 279.21 | 2.95 | 388.31 | 375.48 | 3.30 |
| ST90S100 | 282.96 | 276.87 | 2.15 | 408.92 | 375.69 | 8.13 |
| ST65S100 | 280.46 | 275.46 | 1.78 | 395.93 | 381.68 | 3.60 |
| ST45S100 | 274.41 | 274.27 | 0.05 | 388.44 | 348.76 | 10.22 |
| ST90D35 | 292.77 | 290.13 | 0.90 | 437.52 | 408.39 | 6.66 |
| Specimen Designation | Mid-Span Deflection at Load of 350 kN for Single HFRP and Load of 360 kN for Double HFRP | Error (%) | |
|---|---|---|---|
| DEXP (mm) *a | DFE (mm) *b | ||
| CB | −26.66 | −26.58 | 0.30 |
| U90S100 *c | −19.10 | −19.16 | 0.31 |
| U65S100 *c | −19.19 | −20.29 | 5.73 |
| U45S100 *c | −22.75 | −24.27 | 6.68 |
| U90D35 *d | −14.15 | −13.98 | 1.20 |
| U65D35 *d | −19.14 | −16.49 | 13.85 |
| U45D35 *d | −22.73 | −22.51 | 0.97 |
| ST90S100 *c | −17.14 | −19.02 | 10.97 |
| ST65S100 *c | −17.40 | −19.02 | 9.31 |
| ST45S100 *c | −20.55 | −21.18 | 3.07 |
| ST90D35 *d | −14.76 | −13.47 | 8.74 |
| Symbol | Examined Parameter | Examined Levels |
|---|---|---|
| A | HFRP thickness | 1HFRP, 2HFRP, 4HFRP |
| B | Steel grade | G60, A36 |
| C | Loading scheme | 4PL, 3PL |
| D | Spacing between bolts | 100 mm, 35 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AbouEl-Hamd, O.R.; Sweedan, A.M.I.; El-Ariss, B.; El-Sawy, K.M. Experimental and Numerical Investigation of the Behavior of Steel Beams Strengthened by Bolted Hybrid FRP Composites. Buildings 2023, 13, 824. https://doi.org/10.3390/buildings13030824
AbouEl-Hamd OR, Sweedan AMI, El-Ariss B, El-Sawy KM. Experimental and Numerical Investigation of the Behavior of Steel Beams Strengthened by Bolted Hybrid FRP Composites. Buildings. 2023; 13(3):824. https://doi.org/10.3390/buildings13030824
Chicago/Turabian StyleAbouEl-Hamd, Omnia R., Amr M. I. Sweedan, Bilal El-Ariss, and Khaled M. El-Sawy. 2023. "Experimental and Numerical Investigation of the Behavior of Steel Beams Strengthened by Bolted Hybrid FRP Composites" Buildings 13, no. 3: 824. https://doi.org/10.3390/buildings13030824
APA StyleAbouEl-Hamd, O. R., Sweedan, A. M. I., El-Ariss, B., & El-Sawy, K. M. (2023). Experimental and Numerical Investigation of the Behavior of Steel Beams Strengthened by Bolted Hybrid FRP Composites. Buildings, 13(3), 824. https://doi.org/10.3390/buildings13030824