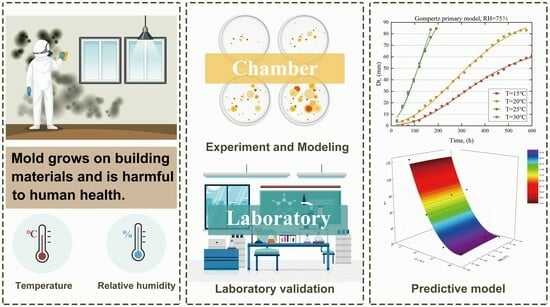
A Predictive Model for the Growth Diameter of Mold under Different Temperatures and Relative Humidities in Indoor Environments

Abstract

A substantial body of evidence suggests that indoor mold exposure is a cause of allergic and respiratory diseases in humans. While models exist for assessing the risk of mold growth on building materials, few study the characteristics of mold growth after germination. This study conducted mold growth experiments in a constant temperature chamber, using four temperature settings of 15, 20, 25 and 30 °C, and three relative humidities of 56 to 61%, 75 to 76% and 83 to 86%. A mold growth prediction model was established using temperature and relative humidity. The accuracy of the model was verified by comparing the sampling and the predicted values in a laboratory environment. The results indicated that reducing the environmental temperature and relative humidity could significantly inhibit the growth of mold, although the inhibitory effects varied. Temperature might play a more critical role. At higher temperatures (25 °C and 30 °C), the growth rate and lag time of mold tended to be consistent and there were differences in the maximum diameter. In the predictive model, the polynomial secondary model for the maximum growth rate and lag time and the Arrhenius–Davey secondary model for the maximum diameter (A) had good predictive effects (Adj.R² > 0.850). It is speculated that temperature is the key factor affecting the maximum growth diameter of mold. The mold growth prediction model could better predict the growth of mold in actual environments without wind Adj.R² > 0.800), but the accuracy of the model decreased under windy conditions (wind velocity < 1 m/s). The mold growth predictive model we established could be used to predict the growth characteristics of mold in windless environments. It also provides control suggestions for the regulation of temperature and relative humidity in indoor environments, supporting indoor thermal environment management and pollutant control, and ensuring indoor human health.

1. Introduction

Residential environments, one of the primary settings for human activities, are where people have the most frequent and intimate contact. As living standards improve, a series of indoor environmental pollution issues have gradually emerged. Among these, mold is a significant factor contributing to indoor air pollution and has increasingly become a global problem in residential buildings [1].

Numerous studies have revealed severe mold contamination in a large number of residences worldwide, posing serious threats to human health [2,3]. Madureira et al. [4] sampled indoor air from 38 homes of asthmatic children and 30 homes of non-asthmatic children in Porto, Portugal. The results showed that the average concentration of indoor fungi in the homes of asthmatic children was 1038 ± 1837 cfu/m³, while it was 524 ± 869 cfu/m³ in the homes of non-asthmatic children. Antova et al. [5] analyzed the exposure and health data of 58,561 children, and demonstrating a significant correlation between indoor mold exposure and children’s respiratory health. Yuexia Sun et al. [6] investigated the increase in adverse health symptoms (such as asthma, rhinitis, pneumonia, etc.) in newly built energy-efficient buildings, identifying mold as one of the main causes. Takigawa et al. [7] measured the concentrations of aldehydes, volatile organic compounds, airborne fungi and dust mite allergens in living rooms in Okayama, Japan, which indicated that increases in benzene and Aspergillus were risk factors for Sick Building Syndrome (SBS) using a logistic regression model [6]. It was estimated by Kanchongkittiphon et al. [8] that over 10% of the population is allergic to mold and house dust mite allergens and this allergic reaction suggests that contact with allergens could lead to allergic symptoms. The most common allergic symptom in adults [9], children [10,11,12] and infants is asthma [13]. The CCHH (China, Children, Home, Health) project conducted a cross-sectional questionnaire survey on pre-school children’s families in ten cities including Chongqing, Beijing, Shanghai, Harbin, etc., from 2010 to 2012 [14], and found that the incidence of certain allergens in residential interiors in the Chongqing area was higher than in other cities. There was a certain correlation (OR > 1) between damp indicators (such as water damage to walls, damp spots, window condensation, etc.) and children’s allergic/respiratory diseases [15,16]. Therefore, the assessment of indoor environmental risk factors caused by air pollution is an important public health issue.

In indoor environments, mold grows on the surfaces and interiors of walls, furniture, doors and other building materials [17]. This not only affects the aesthetics but it also corrodes building materials, leading to cracking and hollowing, thereby reducing the durability and lifespan of these materials. Building materials are susceptible to mold contamination due to two key factors for mold growth: temperature and relative humidity [18]. Compared with other factors (nutritional substances, exposure time, surface roughness, light and oxygen), mold germinates when the temperature and relative humidity are above critical values [19,20,21]. Numerous facts indicate that after a while, mold will reappear and possibly worsen in the original moldy areas and their surroundings on the wall [22,23]. To reveal the relationship between the germination of mold on building materials and the indoor environment, various mold growth models have been established. The International Energy Agency proposed a temperature ratio model in 1990, which uses temperature and humidity to assess the risk of mold growth [24]. Hukka et al. [25] established an empirical model (the VTT model) based on laboratory test data of mold growth on pine and spruce edge materials. Around 2000, Clarke et al. [26] established the isocline model and divided the fungi in buildings into six categories based on critical relative humidity and temperature values, which are used to determine whether there is a risk of mildew in building materials. Nevertheless, most models only reveal the conditions for mold growth and germination, and there has been little study of the process of mold growth. It is difficult for the indoor environment to ensure that all building materials are suitable for inhibiting mold growth; however, some building materials such as wood [27,28] and wallpaper [29,30] are known to be prone to mold growth under suitable conditions. Therefore, appropriate environmental control measures based on mold growth characteristics are needed. To clarify the growth characteristics of indoor mold, it is necessary to apply a mold growth prediction model suitable for indoor environments.

Most existing mold growth prediction models are primarily used in specific food environments to protect food safety by inoculating target molds into standard media or more homogeneous food products. Wawrzyniak et al. [31] used a modified Gompertz model to predict mold growth at temperatures ranging from 12 to 30 °C and water activity (a_w) ranging from 0.8 to 0.9, demonstrating that the modified Gompertz model could predict the fungal population and grain mold risk in barley grain well at different temperatures and a_w values [32]. Other substrate characteristics (pH, salinity, etc.) are also used in modeling. Kosegarten et al. [33] established Gompertz and Gibson models for Aspergillus flavus on media simulating food systems at different temperatures (15, 25, 35 °C), a_w values (0.900, 0.945, 0.990) and pHs. On this basis, secondary models were used to calculate the relationship between environmental factors and the maximum growth rate (${\mu }_m$) and the lag time ($\lambda$) in the primary model. Pei et al. [34] explored the growth of Aspergillus in rice under 16 conditions with different combinations of temperatures and a_w values, and found that the primary model of the Gompertz and Baranyi had different applicability, while the polynomial model was considered the most suitable secondary model for the effect of temperature and a_w. The measurement of mold growth could be achieved through various methods including observing the colony diameter on solid media, and measurements of mycelial dry weight, CFUs, and ergocaloric cholesterol concentration. In particular, for molds, prediction models could be fitted by observing the colony diameter on solid media, thereby controlling the culture environment based on the mold growth rate, a common approach in the field of food protection research. Abellana et al. [35] used a modified Gompertz model to fit the radial growth of Saccharomyces colonies in a flour–wheat medium at different temperatures (5 °C to 30 °C) and a_w values (0.775 to 0.900). Yogendrarajah et al. [36] found that the polynomial model best described the growth rates of mold diameters under the coupled effects of temperature and a_w. It was inferred that using growth diameter rather than mold concentration is more suitable for describing indoor mold growth. Both a_w and relative humidity serve as viable predictors of fungal growth diameter [37,38]. In indoor environments, studies pay more attention to whether there is a risk of mildew on building materials, but few studies focus on the growth characteristics after mildew formation, and traditional research methods might not be sufficient to explore these issues in depth.

In indoor environments, how to determine the appropriate temperature and relative humidity range to inhibit mold growth, how to develop a mold growth prediction model based on temperature and relative humidity, and how environmental parameters affect model parameters and accuracy are problems that require further exploration and solving. This study first delineated three key growth parameters in the process of indoor mold growth. Then, it investigated the influence of temperature and relative humidity on the growth parameters (${\mu }_m$, $\lambda$, $A$) and proposed a prediction method for the growth parameters based on indoor environmental parameters. Finally, a mold growth prediction model was established, which is applicable for predictions in windless environments. The main aims of this study were as follows:

(1)

Investigate the impact of temperature and relative humidity on the growth parameters of mold, identify the key environmental factors and the control ranges, and provide recommendations for environmental control to prevent indoor mold growth;

(2)

Establish a predictive model for mold growth based on indoor temperature and relative humidity, develop appropriate modeling methods to fit the mold growth curve and predict growth parameters, and determine whether relative humidity could be used for mold growth prediction;

(3)

Validate the applicability of the mold growth predictive model in real environments (unventilated and natural ventilation conditions) and analyze the factors influencing the accuracy of the predictive model.

This work established a mold growth diameter prediction model using temperature and relative humidity, clarified the range and direction of inhibiting mold growth through indoor environmental control measures, and provides a reference for indoor mold growth risk assessment and antibacterial measures. This will help alleviate indoor mold pollution, ensuring the health and well-being of residents.

2. Materials and Methods

2.1. Mold Growth Experiments

2.1.1. Mold Strains and Inoculations

According to our previous home investigations and fungal measurements in air and dust in typical residences in Chongqing, China [39,40], as well as in other studies [41,42], Aspergillus niger is a common fungal species that is widely detected in residential environments, causing some allergic or respiratory diseases due to the emitted allergens [16,43]. Therefore, Aspergillus niger (ATCC 16404, same as AS3.3928, American Type Culture Collection (ATCC)) was chosen as inoculation strain, as shown in Figure 1a.

The strains we purchased were stored as lyophilized powders in tubes, so they needed to be activated. Spores suspensions were prepared by washing the cultures with sterile distilled water containing 0.01% (v/v) Tween^® 80 (Merck KGaA, Darmstadt, Germany) [44]. The spore concentration of each suspension was assessed using blood counting plates under a microscope and adjusted if necessary to 106 spores/mL. To minimize the potential impact of the a_w change between the suspension and the growth medium [45], the final suspensions were inoculated into Tsa’s agar medium (90 mm, 15 mL per Petri dish, Czapek Dox Agar, CDA) (medium formulation: sucrose 30.0 g, NaNO₃ 3.0 g, MgSO₄-7H₂O 0.5 g, KCl 0.5 g, FeSO₄-4H₂O 0.01 g, K₂HPO₄ 1.0 g, agar 15.0 g, distilled water 1.0 L, pH 6.0–6.5) as quickly as possible (less than a few minutes) for inoculation, and then incubated for 2 to 3 generations to obtain heavily sporulating cultures. The activation, solution preparation and inoculation of mold was carried out on a clean bench (SJ-CJ-2FDQ, Suzhou Sujie Purification Equipment Co., Ltd., Suzhou, China).

2.1.2. Experimental Conditions

To study the characteristics of the mold growth model, initial mold cultures were grown under controlled temperature and humidity conditions. The molds were cultivated in a laboratory at specific temperatures (15 °C, 20 °C, 25 °C and 30 °C) and relative humidity levels (56 to 61%, 75 to 76%, and 83 to 86%). A constant temperature chamber (Figure 1c) was used to maintain the incubation temperature, while saturated solutions of NaBr, NaCl and KCl were used to control the relative humidities at 56 to 61%, 75 to 76% and 83 to 86%. However, they do not have constant saturation relative humidities from 15 °C to 30 °C [46]. These controlled conditions were primarily used to enable the initial primary and secondary modeling.

2.1.3. Experimental Process

In the chamber, all test samples were placed horizontally in an artificial environment. The chamber had a temperature range of 0 to 55 °C with an accuracy of ±2 °C and a relative humidity range of 60% to 95% with an accuracy of ±5% to ±8%. The chamber had a day–night setting with the regulation of lighting illuminance between 0 and 20,000 lx. To simulate the dynamic variation in a day, the chamber was regulated dynamically every 2 h with the designed temperature and relative humidity values. To avoid large changes in relative humidity in the chamber, before the experiment, we prepared saturated solutions of NaBr, NaCl and KCl in conical flasks, and sterilized them at 121 °C for 20 to 30 min in a high-pressure steam sterilizer. After inoculating the Aspergillus, we injected an appropriate amount of the sterilized and cooled saturated salt solution (about 45 mL) into a Petri dish (φ120 mm, lid outer diameter 128 mm, bottom outer diameter 120 mm, dish height 24.7 mm, wall thickness 2.7 mm), and then placed the inoculated Petri dish (φ90 mm, no lid, lid outer diameter 98 mm, bottom outer diameter 90 mm, dish height 20 mm, wall thickness 2.2 mm) inside it, as is shown in Figure 1b, and finally placed this set-up in the incubator for cultivation. The chamber was examined regularly and adjusted when needed to ensure correspondence between the set points and actual values. To record the daily growth of mold, we removed the Petri dish (φ120 mm) from the chamber as quickly as possible. Simultaneously, we adjusted the air conditioning to match the temperature inside the chamber. The above process was carried out by trained researchers to minimize the impact of sudden environmental changes on mold growth. These long-term cyclic changes continued for 40 days for each experimental condition, ensuring enough time for the mold to germinate and grow. To monitor the growth, we took photos for each sample every 24 h, starting from when mold germination began.

2.2. Modeling

2.2.1. Primary Modeling

To elucidate the growth characteristics of mold, we employed biological models to describe the diameter of the mold growth. There are a multitude of primary models that describe microbial growth from various perspectives, such as the Baranyi, the Gompertz, the three-phase linear primary growth model, etc. [47]. These models provide a mathematical framework that captures the key features of mold growth, allowing us to quantify and predict it under various conditions. These models typically take the form of exponential functions; we used the Gompertz model as an example (Equation (1)).

$$y=a·\exp \left[-\exp \left(b-cx\right)\right]$$

(1)

In the context of mold growth, ‘$x$’ represents the time of growth, while ‘$y$’ denotes the degree of growth. As shown in Figure 2, the degree of growth ‘$y$’ could be expressed as $D_t$ (colony diameter, mm), ln($D_t$), $D_t$/$D_0$ (colony diameter ratio where $D_0$ is the initial value of the colony diameter that could be observed with the naked eye) or ln($D_t$/$D_0$) (logarithmic value of colony diameter ratio) on the plate medium. The choice between these parameters for the degree of growth ‘$y$’ depends on the specific growth conditions and characteristics of the mold. In this study, $D_t$ was chosen to represent the colony diameter.

In Equation (1), the parameters ‘$a$’, ‘$b$’ and ‘$c$’ do not have a direct biological interpretation. However, the growth curve of mold could typically be described using three biologically meaningful parameters: the maximum growth rate (${\mu }_m$), which is the inflection point of the curve and represents the maximum rate at which the mold population increases; the lag time ($\lambda$), which is the x-axis intercept of the tangent at the inflection point and represent the duration before the mold begins to grow exponentially; and the maximum diameter ($A$), which is the intersection of the asymptote and the y-axis that indicates the maximum population size that the mold reaches during the stationary phase of their growth. These growth parameters (${\mu }_m$, $\lambda$, $A$) could be derived from the mathematical parameters ($a$, $b$, $c$) through a transformation [47]. As the Gompertz model and the Logistic model are the two most frequently used models to describe bacterial growth in foods, both the Gompertz model (Equation (2)) and the Logistic model (Equation (3)) after the transformation were chosen to describe the relationship between colony diameter $D_t$ (mm) and growth time (h) of Aspergillus niger, and the fitted plots and model parameters were obtained by nonlinear fitting in OriginPro 2021 (64-bit, Version 2021, OriginLab Corporation, Northampton, MA, USA).

$$D_t=A·exp\left\{-exp\left[\frac{{\mu }_{m}e}{A}\left(\mathsf{\lambda }-\mathrm{t}\right)+1\right]\right\}$$

(2)

$$D_t=\frac{A}{\left\{1+exp\left[\frac{4{\mu }_m}{A}\left(\mathsf{\lambda }-\mathrm{t}\right)+2\right]\right\}}$$

(3)

where $t$ denotes the growth time, h; $\lambda$ indicates the period of growth retardation, h; $A$ is the maximum growth diameter, mm; ${\mu }_m$ is the maximum growth rate, h⁻¹; and $D_t$ is the average mold diameter at time t (h) [48,49]. By utilizing the aforementioned model, we obtained growth parameters (${\mu }_m$, $\lambda$, $A$) through nonlinear fitting using the primary modeling.

2.2.2. Secondary Modeling

In the primary modeling, we discerned the characteristics of mold growth and computed the key parameters. By investigating the interplay between growth parameters and pivotal environmental factors, we were able to devise appropriate strategies for environmental regulation. To gain deeper insights, we leveraged secondary modeling with additional environmental variables. Common secondary models such as the Gibson model [50], Arrhenius–Davey model [51], etc., account for a single environmental factor (commonly temperature) that influences the three biological parameters. In this study, we employed this model to predict the maximum growth rate (${\mu }_m$) and lag time ($\lambda$) (Equations (4) and (5)) using a polynomial model [52], and the maximum diameter ($A$) (Equation (6)) using the Arrhenius–Davey model. Within the polynomial model framework, we found the maximum growth rate (${\mu }_m$) to be relatively small, so we amplified this rate a hundredfold to enhance the calculation accuracy.

$${\mu }_m\times 100=m_0+m_{1}T+m_{2}RH+m_3{T}^2+m_4{RH}^2+m_{5}T\times RH$$

(4)

$$\lambda =n_0+n_{1}T+n_{2}RH+n_3{T}^2+n_4{RH}^2+m_{5}T\times RH$$

(5)

$$A=b\left(T-T_{min}\right)$$

(6)

where $m_i$ and $n_i$ are the coefficients of polynomial fitting, $T$ (°C) is the average temperature, $T_{min}$ (°C) is the cardinal temperature, and $RH$ (%) is the average relative humidity in the environment.

2.2.3. Model Accuracy Evaluation

Given that numerous primary models have not been validated for accuracy [53,54], some models could not accurately predict mold growth in indoor environments [52,55]. The goodness of fit of modeling was determined using the coefficient of determination (${Adj.R}^2$) [49,56], root mean square error ($RMSE$) [31,57], accuracy factor ($A_f$) and deviation factor ($B_f$) [31,38,52]. The $RMSE$ indicates the average error, while $Adj.R^2$ represents the proportion of the variance. $A_f$ is used to describe the model accuracy while $B_f$ is used to evaluate the average difference between the predicted and experimental values. The lower the $RMSE$, the higher the $R^2$ or the closer the $A_f$ value is to 1, the better the model is in predicting mold growth. If $B_f$ < 1, the model predictions are underestimated. Otherwise, it indicates that the predicted value is overestimated. The above coefficients are calculated using Equations (7)–(10):

$$Adj.R^2=1-\frac{\sum _i^n{\left(D_t-D_t^{\prime }\right)}^2}{\sum _i^n{\left(\overline{D_t}-D_t^{\prime }\right)}^2}\times \frac{n-1}{n-p-1}$$

(7)

$$RMSE=\sqrt{\frac{\sum _{i=1}^n{\left(D_t-D_t^{\prime }\right)}^2}{n}}$$

(8)

$$A_f={10}^{\sum _i^n\frac{\left|\lg \left(D_t\right)-\lg \left(D_t^{\prime }\right)\right|}{n}}$$

(9)

$$B_f={10}^{\sum _i^n\frac{\lg \left(D_t\right)-\lg \left(D_t^{\prime }\right)}{n}}$$

(10)

where $D_t$ (mm) and $D_t^{\prime }$ (mm) are the predicted and experimental data, $n$ is the total number of measuring points and $p$ is the number of parameters in the model.

2.3. Laboratory Validation

To evaluate the applicability of the mold growth prediction model in a real environment, an experimental room (5.81 m × 5.03 m × 2.77 m) was constructed for verification. In this environment room, we set the condition with windows and doors completely closed as condition 1, and the condition of windows and doors open for natural ventilation as condition 2. In conditions 1 and 2, we verified whether the mold growth prediction model established in the chamber could predict mold growth. To reduce the impact of random errors during the experiment on the results, we chose 4 points on two diagonals in the room as sampling points, named points 1, 2, 3 and 4, as shown in Figure 1d. Since mold grows slowly during the germination period, the beginning of germination was set as 0 h. Then, mold growth was recorded at 36, 48, 60, 72, 84, 96, 108 and 120 h. A HOBO (UX100-003, range: 20 to 70 °C, ±0.21 °C, 1 to 95%, ±3%, 1 min per sampling) (Figure 1e) and DELTA OHM anemometer (HD103T, range:0 to 5 m/s, ±0.04 m/s, 4 mins per sampling) (Figure 1f) were placed at the center of the room to monitor indoor temperature, relative humidity and wind velocity (Figure 1e,f). To ensure the stability of humidity changes, we used a dehumidifier placed in the center of the room, set the target relative humidity to 75%, and dynamically control the changes in relative humidity.

Thermal conditions within the experimental room were further analyzed using time-series data for temperature, relative humidity and wind velocity. After removing outliers based on the 3σ criteria for the normal distribution test, the average values for temperature, relative humidity and wind velocity were obtained from the experiments [30]. Then, we obtained a secondary model that could predict growth parameters and the above primary model could fit mold growth characteristics in a actual environment. We calculated the average values of the temperature and relative humidity and substituted them into the secondary model to obtain the values of the growth parameters [58] in the laboratory validation.

2.4. Statistics

The mold diameters on the plate medium were measured using the cross-crossing method and recorded as $D_t$ (mm). As the diameter of the colony was small after inoculation at the beginning, photos were taken right above the culture vessel, and the photos were enlarged and measured using ImageJ (64-bit Java 8, Version 1.40, National Institutes of Health, Bethesda, MD, USA). In the chamber environment, the colony diameter was recorded every 24 h. When the colonies covered the entire plate (i.e., $D_t$ was close to 90 mm) or the culturing days exceeded 40 days, cultivation was stopped.

After obtaining the diameter of mold growth, nonlinear fitting was performed using OriginPro 2021 according to the primary models. This determined the fitting effect of the model and obtained a primary growth kinetic model that could reflect the growth changes of mold under different temperatures and humidities over time. Further processing was performed using OriginPro 2021 according to secondary growth models to obtain secondary models that could reflect the growth characteristics of mold under temperature or temperature–humidity coupling effects. During the fitting process, primary mold growth parameters were obtained. In the secondary models, Equations (4)–(6) were used to reflect the relationship between growth parameters (${\mu }_m$, $\lambda$, $A$) and environmental factors (temperature and relative humidity).

In the room environment, due to time and condition constraints, mold could not be cultured for a long time until its death. Only colony diameter data at 0, 36, 48, 60, 72, 84, 96, 108 and 120 h were used for model verification. Each measurement was repeated 3 times for each set of conditions, and the colony diameter $D_t$ was taken as the average of the three measurements. IBM SPSS Statistics 25 (64-bit, Version 25, IBM Corporation, Armonk, NY, USA) was used to calculate the average temperature and relative humidity in the environment with the 3-sigma rule. During the verification process, Microsoft Office Excel 2021 (64-bit, Version 2021, Microsoft Inc., Redmond, Washington, DC, USA) was used to calculate the verification coefficients.

3. Results

3.1. Results of the Primary Modeling

Under the conditions of the chamber, the mold growth sampling data at temperatures of 15, 20, 25 and 30 °C and relative humidities of 56 to 61%, 75 to 76% and 84 to 86% were compiled into modeling data. Using OriginPro 2021 throughout the Gompertz and Logistic models for nonlinear fitting and iterating until convergence, we obtained fitting diagrams and growth parameters. We used ${Adj.R}^2$ to reflect the goodness of fit, and $RMSE$, $A_f$ and $B_f$ to reflect the error between predicted values and actual values.

In Figure 3, the vertical axis is the growth diameter and the horizontal axis is the culture time. The higher the temperature, the closer the curve is to the y-axis, the faster the growth rate of the mold, the smaller the lag time, and the more difficult it is to observe the maximum diameter ($A$). At the same time, the growth curves at 25 °C and 30 °C were relatively close. The maximum growth rate (${\mu }_m$) underwent a process from slow to fast and then slow at 15 °C and 20 °C. However, at a certain temperature, the relative humidity had little effect on the growth characteristics of the mold, and it was difficult to observe from the graph. In addition, the Gompertz model’s curve was smoother than the Logistic model’s curve, which corresponds more to mold growth reproduction theory.

Table 1. Parameters and accuracy index of the Gompertz model in mathematical modeling.

Environmental Factors		Model Parameters			Accuracy Indicators
T (°C)	RH (%)	A (mm)	μm × 100 (h−1)	λ (h)	Adj.R2	RMSE	Af	Bf
15 °C	61%	75.99	14.78	122.74	1.00	0.83	1.03	0.99
	76%	71.26	14.52	108.27	1.00	0.92	1.03	1.00
	86%	71.98	14.13	114.25	1.00	0.63	1.03	1.00
20 °C	59%	89.40	21.43	61.03	1.00	1.04	1.04	1.01
	76%	102.20	20.47	75.86	1.00	1.36	1.04	1.01
	85%	94.89	21.63	76.89	1.00	1.40	1.05	1.03
25 °C	58%	131.32	52.33	27.07	0.99	2.65	1.10	1.03
	75%	111.37	56.04	24.50	1.00	1.91	1.09	1.05
	84%	123.10	54.18	24.23	1.00	1.58	1.05	1.00
30 °C	56%	134.67	60.28	27.03	0.99	3.24	1.18	1.09
	75%	147.82	61.87	32.73	0.99	2.49	1.14	1.07
	84%	122.75	62.96	24.67	0.99	3.09	1.17	1.09

and

Table 2. Parameters and accuracy index of the Logistic model in mathematical modeling.

Environmental Factors		Model Parameters			Accuracy Indicators
T (°C)	RH (%)	A (mm)	μm × 100 (h−1)	λ (h)	Adj.R2	RMSE	Af	Bf
15 °C	61%	70.82	15.62	145.85	0.99	1.34	1.05	1.00
	76%	67.16	15.15	128.71	0.99	1.41	1.06	1.02
	86%	67.27	14.88	136.44	1.00	1.31	1.06	1.02
20 °C	59%	81.90	22.59	77.48	0.99	1.94	1.09	1.04
	76%	88.83	22.23	98.01	1.00	1.75	1.09	1.04
	85%	85.42	23.03	94.89	0.99	2.45	1.12	1.07
25 °C	58%	100.26	56.56	34.65	0.98	3.18	1.12	1.06
	75%	94.00	60.20	31.65	0.99	2.94	1.13	1.08
	84%	97.35	59.21	32.39	1.00	1.56	1.06	1.02
30 °C	56%	102.02	65.07	33.67	0.98	3.94	1.21	1.12
	75%	105.32	66.45	38.62	0.99	3.34	1.17	1.10
	84%	99.12	67.97	31.33	0.98	3.99	1.22	1.12

provide more detailed information on the accuracy of the primary model. Similar to the results in Figure 3, temperature had a greater influence on the model parameters than relative humidity. There was an effect of relative humidity on the model parameters but the validity was small. The temperature had a decisive influence on the maximum diameter ($A$), and a secondary model could be established using a temperature as a single prediction parameter. The maximum growth rate (${\mu }_m$) and lag time ($\lambda$) could be taken into account by the combined effects of temperature and relative humidity. From the perspective of the accuracy index, the higher the temperature, the greater the $RMSE$, indicating that the average error is larger when the temperature is higher, and the $RMSE$ of the Logistic primary model reached over 3 at 30 °C. Comparing Table 1 and Table 2, it can be observed that the two primary models had good prediction abilities for the parameters ($Adj.R^2$ is close to 1), but both showed a large average error of fitting results at a high temperature (30 °C). The Gompertz primary model was better than the Logistic primary model for the fitting of mold growth characteristics, and both were within the acceptable range.

3.2. Results of the Secondary Modeling

The secondary model was based on the primary model to describe the functional relationship between the model parameters and environmental variables (temperature and relative humidity). Firstly, we used OriginPro 2021 to analyze ${\mu }_m$ and $\lambda$ using nonlinear fitting, and then the secondary polynomial coupling on the three-dimensional graph was used to obtain the fitting results for parameters in the secondary model. The parameters of the polynomial model are shown in Equations (11) and (12). Secondly, a two-dimensional prediction diagram using the polynomial model results is presented in Figure 4a,b. Moreover, $A$ in the Gompertz model was substituted into Equation (13) by linear fitting, resulting in coefficients $b$ and $T_{min}$, as shown in Figure 4c.

$${\mu }_m\times 100=-58.74+2.65T+74.50RH+0.01T^2-58.60{RH}^2+0.56T\times RH$$

(11)

$$\lambda =409.44-27.38T+33.31RH+0.47T^2-25.28{RH}^2+0.28\times RH$$

(12)

$$A=4.25\left(T+2.54\right)$$

(13)

As illustrated in Figure 4a,b, the polynomial prediction model demonstrated that temperature had a more significant impact on the model parameters than relative humidity, corroborating the conclusions drawn from Figure 3. As the temperature rose from 15 °C to 30 °C, the maximum growth rate (${\mu }_m$) escalated from 11.20 × 10⁻² h⁻¹ to 65.60 × 10⁻² h⁻¹, while the lag time ($\lambda$) decreased from 118.5 h to 24.0 h. This indicates that an increase in temperature accelerates the growth rate of the mold and reduces the lag time ($\lambda$) of mold growth. However, at the same temperature, the predicted model parameter values between different relative humidity points showed minor differences. Figure 4c further reveals that as the temperature increased, the maximum diameter ($A$) also increased, suggesting that a temperature rise could increase the maximum diameter of mold growth. The specific numerical changes are shown in Table S4.

At the same time, we verified the accuracy of the secondary model. As shown in

Table 3. Accuracy test of growth parameters in secondary modeling.

Equation	Model	Model Parameter	Adj.R2	Af	Bf
(11)	The polynomial model	${\mu }_m$	0.850	1.193	1.001
(12)		$\lambda$	0.923	1.154	1.023
(13)	The Arrhenius–Davey model	$A$	0.894	1.042	1.003

, it is evident that the polynomial and Arrhenius–Davey secondary models provide an acceptable fit for the model parameters. The $Adj.R^2$ for the $\lambda$ was the highest at 0.923, indicating that the polynomial secondary model could predict the $\lambda$ well based on temperature and relative humidity. Simultaneously, the smallest ${\mathrm{A}}_{\mathrm{f}}$ for $A$ suggests that the Arrhenius–Davey secondary model could predict $A$ effectively using temperature. The accuracy test results reveal that the second-order models could predict the model parameters well, with a low likelihood of underestimating the parameters. This outcome demonstrates that the predictions obtained through the secondary models are reliable and could be applied in real environments.

3.3. Results of the Laboratory Verification

Figure 5 represents the average changes in temperature, relative humidity and wind velocity under conditions 1 and 2. The temperature, humidity and wind speed data from the experiments were processed according to the 3-sigma rule to exclude outliers. In condition 1, out of the 7200 data points for temperature (with an average temperature of 24.81 °C and a standard deviation of 0.948 °C), 111 data points (approximately 1.54%) were rejected. In condition 2, out of the 1800 data points for wind speed (with an average wind velocity of 0.02 m/s and a standard deviation of 0.017 m/s), 13 data points (approximately 0.72%) were rejected. Unlike the constant temperature chamber, the temperature in condition 1 showed an upward trend in the first 72 h and a downward trend from 72 to 120 h. The relative humidity also showed dynamic changes between 65% and 80%. After calculation, the average temperature in conditions 1 and 2 was 25 °C and the average relative humidity was 75%. Moreover, the average wind velocity in condition 2 was 0.03 ± 0.02 m/s, while the average wind velocity in condition 1 was 0. The average values of temperature and relative humidity were substituted into Equations (11)–(13), and the model parameters were obtained. Finally, we obtained the Gompertz prediction models under conditions 1 and 2, as shown in Equation (14).

$$D_t=117.05·\exp \left\{-\exp \left[11.51\times {10}^{-3}\left(29.66-t\right)+1\right]\right\}$$

(14)

Subsequently, we compared the mold growth diameters obtained from the four sampling points with Equation (14), as shown in Figure 6. Due to the discontinuity of the mold measurements, we could not obtain the actual change in mold growth diameter within 120 h. The overall trend of mold growth during the logarithmic growth period is consistent with the prediction curve in conditions 1 and 2. The prediction curve could accurately describe the mold growth changes at the four points in condition 1, while in condition 2, the prediction curve predicted a smaller diameter at 0 h, and the actual diameter of mold growth at the four points in the room was significantly lower than the prediction curve between 96 and 120 h. To further illustrate the deviation between the prediction model and the actual sampling, we also used four indicators of model accuracy to evaluate the accuracy of the model predictions. In Table 3, the range of${Adj.R}^2$ in condition 1 was 0.717 to 0.935, while the range of ${Adj.R}^2$ in condition 2 was −0.540 to 0.357, indicating that the prediction model predicted the mold growth diameter under the unventilated conditions better. The range of $RMSE$ changes in condition 1 was 3.115 to 5.835, while in condition 2, it was 7.969 to 11.391. The differences between the predicted and sampling values in condition 2 were greater than that in condition 1. Although the mold growth predictive model in both conditions exhibited a certain degree of overestimation, it produced higher estimation errors ($B_f$ > 1.3) and a lower accuracy ($A_f$ > 1.3) for condition 2.

4. Discussion

4.1. Effect of Temperature and Relative Humidity on Mold Growth

Maintaining the indoor temperature at 15 °C could significantly reduce the growth of mold, and temperature might have a greater effect on the growth and reproduction of mold compared to relative humidity. Temperature had a greater impact on mold than relative humidity, and relative humidity had little effect on the mold growth rate [59] (Table 1 and Table 2), which lacks consistency with the conclusions drawn in some previous studies [34,60,61]. Although temperature changes have a significant impact on mold growth, this effect was not pronounced at higher temperatures (25 °C and 30 °C) (Figure 3). Haoxiang Wu et al. [62] maintained a constant relative humidity during the cultivation of C. cladosporioides and found no significant difference in the growth rate at 19 °C and 28 °C. Penggang Pei et al. [52]’s results align with our findings, demonstrating that the impact of temperature on the growth rate and lag time of mold is limited in high-temperature environments. However, it is noteworthy that Wagner Augusto Müller et al. [63] observed that mold maintains its maximum growth rate (${\mu }_m$) from the outset when in high-temperature conditions ($T$ > 70 °C). Only when the mold reaches its maximum diameter ($A$) do significant differences appear due to varying temperatures (75 °C, 80 °C, 85 °C, 90 °C and 94 °C).

The influence of relative humidity on mold growth is relatively minor, but this does not imply a lack of variation. Pavel Kopecký et al. [64] found that relative humidity significantly affects the concentration of mold in the air, with the mold growth coefficient approximating a function of relative humidity, temperature and surface material. Tamaryn Menneer et al. [37] suggested that exceeding a critical level of relative humidity in the environment may lead to mold growth. Chenqiu Du et al. [30] found that gypsum boards are more likely to induce mold growth in high-humidity environments. In our study, the use of Petri dishes for cultivation during the experimental process might have led to a more pronounced effect of temperature on mold growth, resulting in conclusions that differ from the aforementioned studies. This suggests that future research should consider the use of different growth substrates and investigate the impact of varying relative humidity on airborne mold spores to further explore the influence of relative humidity on mold growth. For the lag time ($\lambda$), a humid environment might increase the likelihood of mold growth [29,47,56]. At 15 °C and 25 °C, the $\lambda$ decreased as relative humidity increased, while the $\lambda$ paradoxically increased at 20 °C and 30 °C. Therefore, it is speculated that the $\lambda$ might not serve as a basis for judging the risk of mold growth, but this needs further analysis.

The experimental results obtained in the chamber indicate that lowering the temperature and relative humidity could reduce the growth rate, slow down its lag time and result in smaller diameters. The ${\mu }_m$ increased with the rise in temperature and relative humidity (Figure 3), which suggests that we should reduce the temperature and relative humidity as much as possible to inhibit mold growth, which is consistent with the conclusions obtained by other studies [37,62,65]. From the perspective of indoor environmental control, based on the aforementioned experimental results (Figure 3 and Figure 4), we believe that low temperature is a key factor in preventing mold growth. However, it is not feasible to continuously reduce the temperature; GB50736-2012 [66] stipulates that the indoor temperature should be 18 to 22 °C with no requirement for relative humidity under winter heating conditions, and the summer temperature should be 26 to 28 °C ($RH$ ≤ 70%). This suggests that the temperature should be controlled at an acceptable but low level to inhibit mold growth in winter and summer and reduce the risk of mold occurrence. At the same time, the different temperature tolerance ranges of the species themselves might lead to differences in the research results; therefore, further subdivisions of the species should be considered.

4.2. Accuracy of the Predictive Model and Parameter Determination

Comparing the two models, the Gompertz model had an average ${Adj.R}^2$ of 0.997, which was slightly higher than the Logistic model’s average${Adj.R}^2$ of 0.990 [67]. The Gompertz model’s average $RMSE$ was 1.762, which is closer to 0 than the Logistic model’s average $RMSE$, indicating that the Gompertz model’s fitting effect is better (Table 1 and Table 2). For accuracy of the two primary models, the $A_f$ and $B_f$ of both models were within the acceptable range [68] but the Gompertz model values were closer, which means that the Gompertz model has a higher accuracy and smaller deviation. Jolanta Wawrzyniak et al. [31] evaluated the risk of mold and its toxins in stored seeds based on a mathematical model of predictive microbiology, and found that the prediction model established based on the modified Gompertz model had a good predictive ability (${Adj.R}^2$ = 0.90, $RMSE$ = 0.547). In this study, the ${Adj.R}^2$under different conditions was above 0.90 (Table 1 and Table 2), but the RMSE was high, which means these two primary models might cause large errors. Table 1 and Table 2 demonstrate the accuracy of primary models in predicting the growth parameters of mold. Based on the above analysis, we could conclude that the Gompertz model demonstrated superior predictive accuracy compared to the Logistic model, so the Gompertz primary model was substituted into the secondary model for the subsequent analysis. Meanwhile, given that these models are self-validated, both types of primary models exhibited a high accuracy.

Based on the Gompertz model, we established predictive models for the three growth parameters. Specifically, we used polynomial models to predict the effects of temperature and relative humidity on ${\mu }_m$and $\lambda$. For $A$, we employed the Arrhenius–Davey secondary model to predict its relationship with temperature. In these secondary models, the environmental parameters were used to predict the growth parameters. According to the accuracy test results (Table 3), the secondary models demonstrated high accuracy in predicting the growth parameters (${Adj.R}^2$ > 0.5). We hypothesize that ${\mu }_m$ and $\lambda$ are more significantly influenced by temperature (Figure 3), and the use of polynomial fitting for secondary modeling might not reduce the impact of relative humidity on the predictive accuracy of the model. This could be due to the failure to logarithmize the recorded mold growth diameter during the calculation process, while the $RMSE$ in Vijay K. Juneja et al.’s [57] study is minimal ($RMSE$ < 0.001), indicating that we did not unify the indicators of the aforementioned studies during the process of mold growth prediction. At the same time, secondary models for predicting the ${\mu }_m$ and $\lambda$ parameters has been a focal point in this research field [34,37,52]. In the process of constructing a prediction model for mold growth, our focus was primarily directed toward the newly introduced growth parameter $A$ and the environmental parameter of relative humidity. An in-depth analysis and discussion have been conducted on these two parameters, providing a comprehensive understanding of their impacts on the mold growth prediction model. This approach not only enhances the accuracy of our prediction model but also contributes to the broader understanding of mold growth dynamics in varying environmental conditions.

Regarding the maximum diameter ($A$), it continued to increase as the temperature rose, although the pattern of change was not uniform at the same temperature. By using temperature as a single environmental factor, the Arrhenius–Davey secondary model could more accurately predict the maximum growth diameter compared to the predictions for the maximum growth rate and lag time. In the process of establishing a secondary model for parameter $A$, we did not consider the combined effects of temperature and relative humidity. This is because temperature played a dominant role in parameter $A$ (Figure 3), and we observed that the effect of temperature on $A$ might show a linear trend, so we used the Arrhenius–Davey secondary model to predict parameter $A$. Unlike the indoor environment field, previous studies have focused more on the maximum growth rate and lag time, with relatively less mathematical modeling for the maximum growth diameter $A$ [47,53], except for Penggang Pei et al. [52]’s introduction of $A$ in the Baranyi model, which was not used in his research. We believe that the maximum growth diameter $A$ is equally important because, in indoor environments, the area of mold growth might be an important factor that affects the distribution of indoor mold aerosols [69]. Therefore, we also conducted secondary modeling for parameter $A$, and the model was found to have a good prediction ability (${Adj.R}^2$ > 0.800).

Then, an analysis is carried out from the perspective of factors influencing growth parameters. It could be seen that the temperature, relative humidity and wind speed in the environment affected the accuracy of the growth prediction model by influencing the growth parameters of the prediction model. In the process of building this model, the selection and cultivation of the species [62], the measurement of the mold diameter [34], the choice of primary and secondary models [63], the range of temperatures [62] and relative humidities [62] in the chamber and the ratio of the culture medium [54,63] might have affected the accuracy of the model. It is worth noting that most studies choose a_w as the main factor affecting mold growth in the field of food protection [50,70]. Among them, Wagner Augusto Müller et al. [63] chose relative humidity and a_w as two factors to describe the physicochemical changes on the surface of the culture medium. Tamaryn Menneer et al. [37] successfully predicted the mold risk index in living rooms and bedrooms using relative humidity and temperature. In this study, the selection of water activity (a_w) and relative humidity was based on the specific research questions and objectives. We considered the impact of two environmental factors, temperature and relative humidity, on ${\mu }_m$ and $\lambda$, and established a secondary model accordingly. In the context of indoor environment research, we focused more on the relative humidity in the environment. This is because we aimed to regulate the relative humidity in the indoor environment by studying the growth characteristics of mold. There is a strong correlation between relative humidity and the concentration of airborne mold spores in indoor environments [71]. The higher the relative humidity, the more severe the indoor mold contamination, which poses a higher health risk to humans [2,4].

The mold growth prediction model developed in this study is composed of primary and secondary models. Initially, the Gompertz primary model was used to predict growth parameters based on sampling data of mold diameter. Subsequently, the Arrhenius–Davey model was employed to establish a secondary prediction model for the maximum growth diameter ($A$) as a function of temperature. Furthermore, a polynomial model was utilized to construct a secondary prediction model for the maximum growth rate (${\mu }_m$) and lag time ($\lambda$) in response to temperature and relative humidity. Ultimately, by obtaining temperature and relative humidity from the actual environment, we could calculate the mold growth prediction curve under specific conditions, thereby achieving the prediction of mold growth characteristics in indoor environments.

4.3. Analysis of Laboratory Validation Results

In the laboratory validation, it could be inferred that the prediction model could make good predictions in condition 1, indicating that the prediction model could be used to predict mold growth in the logarithmic growth period under unventilated conditions. In the prediction study of the mold growth model [38,50,53], an $Adj.R^2$ above 0.80 indicates that the established model has a good prediction ability. Wagner Augusto Müller et al. [63] analyzed the inactivation of Aspergillus fumigatus in apple juice and suggested that if $A_f$ and $B_f$ are between 0.9 and 1.05, the prediction model could be considered accurate. Martina Koňuchová et al. [38] also conducted secondary modeling and subsequent optimization, resulting in an $Adj.R^2$ exceeding 0.950, indicating a high degree of accuracy of the model. Prior to the optimization, the model’s $Adj.R^2$ for the lag time ranged from 0.685 to 0.808 without square root transformations. The $Adj.R^2$ coefficient serves as a measure of the model’s accuracy, allowing for a comparison of the model’s performance before and after optimization. This significant increase in the $Adj.R^2$ post-optimization demonstrates the effectiveness of the optimization process in enhancing the model’s accuracy. In our study, the $Adj.R^2$ values of four points in condition 1 were also above 0.70 and below 0.40 in condition 2 (

Table 4. Verification results of the prediction model at points 1–4 in laboratory verification.

Condition	Adj.R2				RMSE
	Point 1	Point 2	Point 3	Point 4	Point 1	Point 2	Point 3	Point 4
1	0.935	0.717	0.934	0.806	3.208	5.835	3.115	5.106
2	0.357	−0.540	0.022	−0.422	7.969	10.832	9.124	11.391
/	$A_f$				$B_f$
1	1.166	1.256	1.151	1.252	1.132	1.256	1.141	1.252
2	1.380	1.561	1.418	1.600	1.380	1.413	1.390	1.600

), suggesting that the mold growth prediction model established in this study could be used for mold growth prediction in unventilated environments. It is noteworthy that in this study, the $Adj.R^2$ for points 2 and 4 in condition 2 were both less than 0, as the prediction model was used to validate uncertain conditions. The $RMSE$ represents the average deviation between the predicted values from the model and the actual measured values. The $RMSE$ in condition 2 was 2 to 3 times that of condition 1, which is consistent with the conclusion drawn from the $Adj.R^2$. When the prediction model is applied to windy conditions, significant errors might occur. Therefore, under windy conditions, the prediction model established in this study is not recommended.

In the laboratory validation, the average wind speed was observed to be 0 in condition 1 (Figure 5). This was due to the closure of doors and windows during the experiment, coupled with the prohibition of any activities within the environment. However, in real environments, particularly in areas frequently occupied by individuals, minor random airflows are often generated due to variations in human activity [72], making these areas more representative of actual environments. Nevertheless, the generation of minor random airflows is difficult to achieve through human activity in this laboratory. Therefore, we opened the doors and windows in the laboratory (condition 2), resulting in a minor airflow distribution within the room, which served to simulate minor airflow variations in real environments. The prediction model established in condition 2 tended to overestimate the mold growth (Figure 6). However, under windless conditions, the diameter of mold growth at the four points varied within an acceptable range. In Table 4, the $A_f$ in condition 1 was significantly smaller than that in condition 2 and is closer to 1. However, the $B_f$ in condition 1 is also greater than 1, indicating that the model might overestimate the actual results. During the construction of this mold growth prediction model, we used the average values of temperature and relative humidity, as these environmental parameters, including wind velocity, are continuously changing in real environments. Therefore, in future research, we should establish predictions of mold growth diameter within a predictable range based on the variation range of environmental parameters, centered around the average value. This approach is acceptable in the field of indoor environments.

On the other hand, this study found that wind speed had an inhibitory effect on mold growth (Figure 6a). The experimental area in this study is an area with calm winds and small annual wind speeds [73]. The real-time wind speeds monitored in condition 2 were all less than 0.1 m/s (0.03 ± 0.02 m/s), which could be ignored, so the impact of wind speed changes on mold growth was minimal. The slow growth of mold might be due to the interference of outdoor airflow during the entire experiment (the windows were open under natural ventilation conditions), and the fresh outdoor air might have the effect of exhausting waste gas. In future research, we plan to build a corresponding experimental platform and ventilation system to further study the impact of airflow and introduce new variables or correction indicators to the prediction model for mold growth.

4.4. Limitations

This study initially employed a specialized humidity-controlled Petri dish for relative humidity control (Figure 1b), acknowledging that the constant relative humidity might vary with environmental temperature changes [46]. The Petri dish, used as the growth substrate during the cultivation process, provided ample nutrients, contrasting with the nutrient-deficient surfaces of building materials (such as wood, stainless steel, plastic, etc.) [54,74]. Future research could consider using different growth substrates to cultivate mold, exploring the impact of different substrates on mold growth characteristics and refining the constructed mold growth prediction model. This study only used Aspergillus as the culture strain, and the conclusions drawn are only applicable to this strain. We should select other types of strains common in indoor environments to carry out cultivation experiments at different temperatures and relative humidities [17], thereby refining the research conclusions in the future. Secondly, this study only used a polynomial secondary model for the maximum growth rate (${\mu }_m$) and lag time ($\lambda$), and the Arrhenius–Davey secondary model for the maximum growth diameter ($A$) to predict growth parameters, without a horizontal comparison with other secondary model modeling methods, resulting in a lack of credibility in the conclusions drawn. Subsequent work could be based on the data obtained in this study, use other modeling methods, establish different mold growth prediction models, compare the differences between models horizontally, and conduct experimental verification in real-world environments. Finally, this study did not delve into the impact of airflow on mold growth, only verifying the model’s accuracy under natural ventilation conditions (wind velocity < 1 m/s), where the impact of wind speed on mold growth could be almost ignored. The lack of wind velocity in the constructed mold growth model might be the main reason for the model’s inaccurate prediction. The objective of future studies should consider introducing wind speed as a factor, establish a prediction model suitable for general indoor ventilation conditions (wind velocity is 0.2 to 0.3 m/s) and verify the model’s accuracy by creating different ventilation volumes in real environmental conditions.

5. Conclusions

This study first proposed a model for predicting mold diameter growth based on temperature and relative humidity. Then, it clarified the trends of ${\mu }_m$ and $\lambda$ with temperature and relative humidity and obtained control recommendations for the chamber. Finally, it validated the prediction ability of the model in real environments. The results can be summarized as follows:

(1)

Our research cultivated mold on a medium under constant temperature and relative humidity conditions. We found that reducing the temperature and relative humidity could significantly inhibit mold growth, but the inhibitory effects varied. Temperature might play a more important role; the maximum growth (${\mu }_m$) rate and diameter ($A$) of the mold increased as the temperature increased, while the lag time ($\lambda$) decreased. At higher temperatures (25 °C and 30 °C), the rate of change in mold growth and lag time might become consistent, and we speculate that the main difference might appear in the maximum diameter ($A$).

(2)

We utilized the diameter of mold growth under varying temperatures and relative humidity levels to derive growth parameters (${\mu }_m$, $\lambda$, $A$) through nonlinear fitting methods. Our findings indicate that these growth parameters could effectively depict the growth process of the mold. The primary model was able to accurately calculate these growth parameters, although it is important to note that temperature and relative humidity might influence the precision of these parameters. Compared to the Logistic model (${Adj.R}^2$ = 0.990), the Gompertz primary model demonstrated superior predictive performance for the growth parameters (${Adj.R}^2$ = 0.997). Therefore, the Gompertz primary model is more suitable for calculating growth parameters in indoor environments.

(3)

We developed a secondary model based on environmental parameter changes to predict growth parameters (${\mu }_m$, $\lambda$, $A$), established a mold growth prediction model and validated the model under windless and windy conditions. We concluded that the polynomial secondary model for the maximum growth rate (${\mu }_m$) and lag time ($\lambda$), and the Arrhenius–Davey secondary model for the maximum growth diameter ($A$) demonstrated good predictive performances (${Adj.R}^2$ > 0.850). Relative humidity was found to be a useful factor in constructing the mold growth prediction model. This mold growth prediction model was able to predict mold growth under windless conditions in real-world environments fairly well (${Adj.R}^2$ > 0.700). However, the model’s accuracy decreased (${Adj.R}^2$ < 0.400) under windy conditions (wind velocity < 1 m/s).

This work established a predictive growth model based on temperature and relative humidity, providing temperature and relative humidity control suggestions for inhibiting indoor mold growth. Moreover, it offers theoretical data support for source control of mold, contributing to the thermal environment regulation and pollutant control in buildings, thereby ensuring people’s well-being.