Next Article in Journal
Career in Geology: An Educational Project in Geosciences for the Enhancement of Student Learning in STEM Disciplines
Previous Article in Journal
Defining Regional and Local Sediment Sources in the Ancestral Colorado River System: A Heavy Mineral Study of a Mixed Provenance Unit in the Fish Creek-Vallecito Basin, Southern California
Previous Article in Special Issue
Integrated Characterization and Analysis of a Slow-Moving Landslide Using Geotechnical and Geophysical Methods
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 13
Issue 2
10.3390/geosciences13020049
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

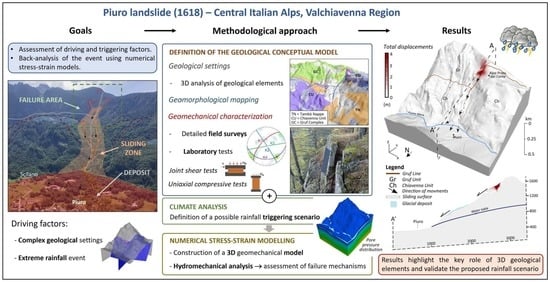
Piuro Landslide: 3D Hydromechanical Numerical Modelling of the 1618 Event

by
Andrea Morcioni
*,
Tiziana Apuani
and
Francesco Cecinato
Dipartimento di Scienze della Terra ‘A. Desio’, Università degli Studi di Milano, Via Mangiagalli, 34, 20133 Milan, Italy
*
Author to whom correspondence should be addressed.
Geosciences 2023, 13(2), 49; https://doi.org/10.3390/geosciences13020049
Submission received: 30 November 2022 / Revised: 31 January 2023 / Accepted: 2 February 2023 / Published: 5 February 2023
(This article belongs to the Special Issue Landslide Characteristics and Susceptibility Assessment)
Browse Figures
Review Reports Versions Notes

Abstract

:
The Piuro 1618 landslide represents a well-known case history of a large Alpine landslide. It destroyed the ancient village of Piuro (Italian Bregaglia Valley), renowned as an important trading center between the Mediterranean region and Northern Europe. The event had a significant impact among communities of all Alpine regions and was well documented by chronicles and paintings during subsequent decades. However, some aspects, such as the geometry reconstruction of the landslide body, the location of the landslide scarp, and its dynamics, remained undefined in previous studies, and a geomechanical characterization of the failure area is completely missing. Using field and laboratory analysis followed by stress–strain numerical modelling, this work develops a 3D conceptual geomechanical model of the slope considering its complex geological framework. The aim is to back-analyze the 1618 event, defining predisposing and triggering factors of the sliding event, and providing verifications on the geometry and location of the failure scar, as well as on the landslide dynamics. A coupled hydro-mechanical analysis with a 3D numerical approach is presented, assuming a rainfall scenario as a possible triggering factor. Simulated displacement and the development of a deep region of shear strain localization at a depth roughly corresponding to that of the detected Piuro sliding surface, allow us to highlight the mechanical role of geological elements outcropping along the slope and to validate the proposed scenario as a likely triggering factor for the 1618 event.

Graphical Abstract

1. Introduction

On 4 September 1618, a large landslide destroyed the ancient village of Piuro causing the death of at least 1000 people. The village of Piuro, located in the middle of the Central Alps (Italian Bregaglia Valley, Figure 1a,b), was an important trading center between the Mediterranean region and Northern Europe, well known for its silk trade and soapstone production. Therefore, the event had a significant social and economic impact among communities of all Alpine regions and was well documented by chronicles and paintings during the subsequent decades [1].
Shortly after the occurrence of the landslide event, different hypotheses were made within the local community to explain why it happened. Some ascribed it to divine punishment against an exaggerated opulence earned with commercial trades, others related it to the heavy rainfall occurring just before the event, and yet others blamed it on an earthquake caused by “very strong underground winds locked up in the many cavities of the mountain”, mined to extract stones. During past decades, based on historical documents and paintings, some authors started to analyze the landslide event in order to define geometries, volumes, and preparatory and triggering factors. Previous studies collected in [2] suggested a possible detachment zone of the landslide and the extent of its deposit. The triggering cause was identified as strong rainfall, as suggested by historical sources describing how the catastrophic event was preceded by heavy rain affecting the Piuro area for the entire previous week [1]. However, the lack of a scientific approach left several questions open, such as the precise location and geometry of the landslide scar and its deposit, the volume of the landslide body, as well as the sliding mechanism. In recent years, the Interreg AMALPI18 project aimed at promoting the scientific knowledge of some large Alpine landslides between the Swiss and Italian territories, including that of Piuro, to raise awareness on hydrogeological instability topics through a cross-border geo-cultural trail (the AMALPI Trek). In this framework, [3] identified the landslide deposit by providing a reconstruction of its geometry and volumes based on geological and geomorphological surveys and on the stratigraphic analysis of two boreholes drilled in the Piuro Valley floor. Moreover, the work by [3] confirmed the location of the landslide scars by the observation of trenches and scarps affecting the southern valley slope. Based on field surveys, a relation with geological elements was highlighted, and two possible scars were outlined by the alignment of morpho-structures.
The 1618 Piuro landslide represents a famous case history of a large Alpine landslide with complex kinematics, induced by extreme climatic conditions [1]. It occurred during the so-called Little Ice Age (LIA), characterized worldwide by colder temperatures [4], snowy winters, and dry summers with frequent flooding. The consequences of such peculiar climatic conditions are documented in the geomorphological activity, especially in soil erosion processes, debris-flow activities, and floodings [5]. During this period, between the 16th and 19th centuries, several large landslides also occurred in the Alpine region (e.g., Monte Crenone and Arth-Goldau rock avalanches [6,7]). The climatic conditions, peculiar to that period, may have favored the development of such gravity phenomena; although, due to the lack of meteorological data, quantitative cause–effect analysis may only be hypothesized [8].
In the literature, rainfalls, rapid snowmelts, and the physical interaction between hydraulic and mechanical processes are considered the most significant factors causing slope failures [9]. In the Alpine environment, there are several examples of slope collapse induced by water pressure increase, including Val Pola 1987 [10], Brenva 1997 [11], Preonzo 2012 [12], Cimaganda 2012 [13], and Cengalo 2017 [14]. In other cases, pore pressure has been deemed responsible for triggering a period of accelerating downslope movement leading to a confined failure event, as, for example, in the Ruinon landslide [15], the Vallemaggia landslide [16], or the La Saxe landslide [17].
In the Alpine environment, initial substantial rock mass damage is generally linked to glacial cycles causing cyclic mechanical loading and unloading to the valley flanks [18,19,20]. Then, hydro-mechanical (HM) loading is deemed responsible for episodic movement and progressive weakening of the rock mass [21]. A seismic or a heavy rainfall event might generate further damage, representing the final collapse trigger leading to a toe breakout or catastrophic slope collapse [16,22,23].
Monotonic or cyclic surface temperature variations, such as those induced by deglaciation and climate change, have been shown by several authors to cause progressive rock weakening (e.g., [24,25,26,27,28]), representing preparatory factors to slope failure. However, in this work, they can be considered of secondary importance, since the role of complex three-dimensional geology and HM loading clearly dominates the landslide initiation mechanisms. A number of works (e.g., [29,30,31,32,33]) also identified thermo-mechanical (TM) couplings at the basal shear surface, with particular reference to frictional heating and thermal pressurization, as playing a key role in promoting failure and the dynamic evolution of landslides. However, such TM effects typically apply to the case of deep-seated landslides with strain localization in clayey shear bands, whereas the development of the Piuro failure mechanism was quite clearly dominated by brittle rock fracturing behavior resulting from a complex geological and tectonic framework.
The concept of progressive degradation of rock masses can be explored via numerical modelling and applied to simulate and study the evolution of a slope failure process [34,35,36,37]. Triggering factors can be introduced to reproduce the collapse of a slope (so-called back-analysis) or to assess different future instability scenarios. Among others, limit equilibrium (LEM), finite element (FEM), finite difference (FDM), and discrete element (DEM) methods are widely used for the understanding and management of landslides [38,39,40]. HM couplings between the internal state of stress of rock slopes and changing piezometric levels have been addressed in many detailed studies focused on large landslides (e.g., see [41,42]).
Large landslides with a complex geological structure are often difficult to analyze using classical modeling methods due to their complex kinematics and hydrological features [43,44]. Most of the published modelling works to analyze the stability of large-scale landslides have been conducted with a two-dimensional approach, even if in most cases they represent a typical three-dimensional problem. A two dimensional approach leads to neglecting structural and morphological differences across the failure surface, as well as the development of localized pore pressure changes induced by topographical constraints [45].
Geosciences 13 00049 g001 550
Figure 1. (a) Location of the study area; (b) Satellite photo of the study area showing the location of the failure area, the extent of the 3D model, and geomorphological features characterizing the Valley; (c) Historical drawings showing the village of Piuro before and after the 1618 event [2]; (d) Geological settings of the Italian Bregaglia Valley (from CROP project, [46]); geological cross section are reported in [3].
Figure 1. (a) Location of the study area; (b) Satellite photo of the study area showing the location of the failure area, the extent of the 3D model, and geomorphological features characterizing the Valley; (c) Historical drawings showing the village of Piuro before and after the 1618 event [2]; (d) Geological settings of the Italian Bregaglia Valley (from CROP project, [46]); geological cross section are reported in [3].
Geosciences 13 00049 g001
In this work, a hydro-mechanical analysis of the Piuro landslide with a 3D numerical approach is presented, preceded by a careful geomechanical and geomorphological reconstruction of the detachment area. The aim is to back-analyze the 1618 event, defining preparatory and triggering factors, and providing verifications on the geometry and location of the failure scar, as well as on its kinematics. The assessment of stress–strain fields is aimed at reproducing the development of the slip surface without introducing any prior knowledge of its location in the model. Simulated outputs are then compared with the observed one in the field. The study aims at giving a contribution to the understanding of HM processes driving failure in rock masses, highlighting the influence of climatic factors in the evolution of Alpine slopes.
The paper is structured as follows: In Section 2.1, the study area is described, focusing on the main geological, geomorphological, and geomechanical features connected to the Piuro landslide. In Section 2.2 the geomechanical conceptual model of the slope is built and the modelling procedure is discussed: a 3D finite difference method (FDM) approach was adopted. An HM fully coupled analysis was performed, considering a rainfall event as a triggering factor. Results are presented in Section 3 focusing on the simulated stress–strain fields in the model domain. Discussions about the performed analyses and conclusions are provided in Section 4 and Section 5, respectively.

2. Materials and Methods

2.1. Piuro Landslide

The village of Piuro is located in the Italian Bregaglia Valley, between the village of Chiavenna and the border with Switzerland (Figure 1a,b). The failure area of the 1618 event is placed on the southern slope of the valley, between 1300 and 1700 m a.s.l., east to the locality “Alpe Prato del Conte”. The dynamic of the landslide event is described in historical writings and chronicles collected by [1]. The sliding mass is described as a “mixture of rocks, mud and water that slid down the slope”, reaching the bottom of the valley and wiping out the ancient village of Piuro (Figure 1c). Dust and debris covered the entire valley as far as the nearby town of Chiavenna, where the event was distinctly heard. The Mera River, which flows through the valley, was dammed for a few hours. According to historical writings, a large area upstream of the landslide deposit was submerged by a lake created by the Mera River, until the water overflowed, without flooding the town of Chiavenna [47]. The volume of the sliding mass is estimated at values of 5–9.5 Mm3 based on the stratigraphical reconstruction of the landslide deposit on the Piuro Plain [3]. Historical sources [2] testify that the catastrophic event was preceded by heavy rainfall that affected the area for the whole week preceding the event. The day before the failure event, instabilities such as new fractures and noises were noted along the slope. Mudslides and rockfalls also reached the village area only a few hours before the event, destroying some forests and crops.

2.1.1. Geological Settings

The geological framework of the Italian Bregaglia Valley is of particular complexity as it crosscuts the stack of the Upper and Middle Penninic Nappes, which include, from top to bottom, the Suretta and Tambò nappes, the Chiavenna unit, and the Gruf complex (Figure 1d; see also the geological map presented in [3] for geological cross-sections). While the northern slope is mainly composed by gneissic rocks and micaschists belonging to the crystalline basement units of the Tambò and Suretta Nappe (Middle and Upper Penninic), on the southern slope, mafic and ultramafic rocks of the Chiavenna unit prevail. The regional tectonic line known as the Gruf Line runs in the upper portion of the southern slope, almost parallel to the valley axis (E-W) and is characterized by a recrystallized and verticalized mylonitic rock band (Figure 1d). The Gruf Line is believed to be an extension of the Engadine Line [48,49,50,51]. Recent seismicity and morphological evidences along the Engadine–Gruf system [49] shows that these elements could be still active [52,53]. In correspondence of the detachment zone of the Piuro landslide, the Gruf Line is dislocated by a sub-vertical fault directed approximately north–south (Figure 1d). To the north of the Gruf Line, ultramafic rocks of the Chiavenna unit with intercalated gneissic bodies of the Tambò unit are present; to the south, migmatitic gneissic rocks of the Gruf complex outcrop. The fault puts the ultramafic rocks of the Chiavenna unit in contact with the migmatitic gneissic ones of the Gruf complex (Figure 1d). This tectonic framework with important rheological differences could be one of the main predisposing factors leading to gravitational instability along the slope.
The Chiavenna unit exhibits banded amphibolites, massive amphibolites, ultramafites (serpentinites with olivine and magnetite, talc schists, chlorite schists, and amphibole schists), and marbles. In correspondence of the Piuro slope, this unit is mainly composed of banded amphibolites with biotite or epidote, and rarely clinopyroxenes, and massive amphibolites made by millimetric to centimetric hornblende and plagioclase [47]. The Gruf complex includes biotite-feldspar migmatitic gneiss [54]. Biotite orthogneiss with abundant centimetric mafic enclaves and migmatitic paragneiss with alternation of leucocratic (quartz and feldspar) and melanocratic (biotite, sillimanite, and garnet) centimetric bands outcrops along the Piuro detachment zone [46].
Concerning the Tambò bodies pinched with the Chiavenna ones, the most widespread rocks are paragneiss composed by millimetric to centimetric bands of quartz and quartz with feldspar layers alternated to biotite or white mica rich gneiss.

2.1.2. Geomorphological Settings

The Quaternary geomorphological evolution of the Bregaglia Valley is related to the superposition of glacial, gravitational, and alluvial processes. During the Last Glacial Maximum (LGM), Engadin glacier filled the whole valley, and only the highest peaks and ridges were ice-free [55]. The trimline of the LGM glaciers in the Italian Bregaglia Valley varies from 2250 m a.s.l. to 2170 m a.s.l. moving east to west [56], and minor lateral glaciers were confined at higher altitudes.
The southern slope is morphologically articulated, with steep portions interrupted by plateaus and terraces, where glacial deposits are well preserved with morainic ridges stretched parallel to the main valley axis (E-W). Trenches and counter-slopes that highlight areas subject to deep gravitational slope deformations (DSGDs) are widespread along the entire slope (Figure 1b). They are particularly concentrated at an elevation of about 1300 m a.s.l., where morphological conditions and the presence of the sub-vertical tectonic lineament (Gruf Line) may have promoted their development with a direction parallel to the valley axis. As shown by [49], the alignment of DSGDs on the southern slope suggests a correlation between slope instability and the geological structure of the valley. In addition, numerous scarps and detachment zones affect glacial terraces on both sides of the valley, reflecting the intense post-glacial activity of the DSGDs. As evidence of the intense geomorphological activity, the valley has been recently affected by significant landslide events which strongly interacted with anthropic activities. In August 2017, a large mass of rock material with volumes comparable to those of the Piuro event, failed from the slopes of the Cengalo Peak, destroying part of the village of Bondo and permanently altering the morphology of the valley [14]. In August 2019, a rockslide of several thousand of cubic meters affected the slopes located north of the village of Villa di Chiavenna, causing the evacuation of some inhabitants. More recently, in July 2021, the Piuro area was affected by a debris flow detached from the northern slope in correspondence with the Perandone Valley. It was triggered by heavy rainfalls and caused the interruption of the national road SS37 connecting Chiavenna with Switzerland.
To characterize the geomorphological features related to the 1618 landslide event, field surveys were carried out along the slope, identifying a failure zone, a sliding/accumulation zone and a deposition zone (Figure 2a).
Focusing around the area affected by the detachment, steep scarps are observed in correspondence of the Alpe Prato del Conte locality at an altitude of about 1430 m a.s.l. (Figure 2b and Figure 3a–c). Here, flat morphologies covered by glacial deposits are abruptly interrupted by trenches and steep rock scarps. Trenches have an ESE-WNW orientation and are characterized by a metric opening whose walls consist of strongly disjointed rock masses (Figure 3d).
The rock scarps are tens of meters high and have a variable orientation moving eastward. At the Alpe Prato del Conte locality they are consistent with the direction of the trenches (ESE-WNW), varying to E-W and then NE-SW, moving eastward (Figure 2b and Figure 3a–c). Other rock scarps with NE-SW orientation are clearly evident upstream of the Alpe Prato del Conte toward the Mottaccio locality, at an elevation of about 1700 m a.s.l. (Figure 2b and Figure 3a–c).
According to [3] and other previous works [2], the rock scarps at Alpe Prato del Conte represent the area where slope failure occurred during the 1618 event, while the upper scarps may have been originated by secondary gravitational events related to detensioning processes. A coeval genesis between lower and upper scarps is not visible in the field but cannot be completely excluded.
Rock scarps are still active, as highlighted by rockfall deposits present at their base without vegetation and featuring small boulders, that become larger moving downstream. From the failure area moving southward, toward the valley floor, chaotic deposits are present with metric rock boulders, often in a silty and sandy matrix (Figure 3e). These deposits are ascribed to the 1618 event [3]. The sliding mass, while moving down, involved the glacial deposits constituting the morphological terrace of Alpe Prato del Conte, Pradella di Piuro, and Alpe Moscone, which are clearly cut by a north–south morphological incision.

2.1.3. Geomechanical Surveys

Geomechanical surveys, carried out along the few accessible walls of the main scarp, showed a high variability of the mechanical quality of rock masses related to lithology and fracturing degree. Following the ISRM suggested methods [56], four detailed geomechanical surveys were performed in the detachment area of the 1618 event (Figure 2b,c).
Overall, four main discontinuity systems can be recognized: 300°/65°(K1), 60°/80° (K2), 180°/30° (K3), 350°/85° (K4). K1 is set along the dominant foliation planes parallel to the Gruf Line, which is directed about 60°–240°, cutting the valley axis at a low angle. It shows smooth surfaces with mean joint roughness coefficient (JRC) values of 8 and joint compressive strength (JCS) of 110 MPa, detected following the ISRM suggested methods [49]. The second one is consistent with the regional 330°–150° directed lineaments, widespread on both sides of the valley and responsible for major secondary valley incisions. Joints show features of shear kinematics with smooth surfaces (mean JRC values of 6 and JCS of 150 MPa). K3 is a planar system with sub-horizontal surfaces cutting the vertical ones. It plays a significant role in the definition of instability blocks along the slope. Joint surfaces show roughness features with mean JRC values of 11 and JCS of 100 MPa. The fourth discontinuity system dips vertically to the north and is mainly related to singular discontinuities with high persistency and very high spacing (>1 m). Joint surfaces are rough (mean JRC values of 9 and JCS of 115 MPa).
The calculated RMR (rock mass rating; [57]) and the evaluated GSI (geological strength index; [58]) reveal a generally discrete to good rock mass mechanical quality (RMR ranging from 59 to 74, GSI ranging from 55 to 65; see Figure 2b). Due to a more intense fracturing and a higher weathering degree of the rock masses, lower values were detected at the Alpe Prato del Conte close to the traction fractures and along the main scarps of the lower niche.
Moreover, in correspondence of the Mottaccio locality, upstream of the detachment zone, disjointed rock masses (with metric openings of discontinuities) were detected. The fracturing condition is predominantly subvertical with E-W and N-S directions; two sets of discontinuities with lower inclination are also present, one dipping toward NW and one dipping to E horizontally. The discontinuity network isolates cubic blocks greater than one cubic meter and represent a preferential zone of water infiltration during rainfalls.
According to the orientation of the main scarps presented in Section 2.1.2, the right flank of the 1618 event is set along the K1 discontinuity system, while the left flank is set along the K2 system (Figure 2). As shown by kinematic analysis, gravitational instability along the slope is favored by the orientation of the vertical joint systems relative to the slope direction. High persistent K1 and K2 shear surfaces may act as a basal sliding plane of significant volumes of rock material, which can be isolated upstream by the K4 tensile system or even by the planar K3 system. Moreover, in the upper part of the slope, in correspondence of the Mottaccio locality, the presence of disarticulated rock masses with highly persistent and opened joints leads to rockfalls events, mainly as toppling or sliding evolution of blocks and rock towers.

2.1.4. Laboratory Tests

A rock sample collection campaign was carried out in the area of the 1618 landslide detachment. To study the mechanical behavior of intact rock and discontinuities, four uniaxial compression tests under unsaturated conditions and a direct joint shear test of one representative surface (K1 set in Figure 2c and Figure 3c) were conducted according to ASTM standards (D7012—14 [59] and D5607—08 [60]). For this work, gneissic samples belonging to the Gruf complex, collected at the upper scarp along the tectonic contact with the Chiavenna unit, were tested. The lithology is characterized by migmatitic paragneiss with alternation of leucocratic (quartz and feldspar) and melanocratic (biotite and sillimanite) millimetric bands. The rock exhibits a mean uniaxial compressive strength (UCS) of 105 MPa with a Young modulus (E) of 35 GPa and a Poisson ratio (υ) of 0.3. The dominant discontinuity belonging to the K1 system was also sampled at the upper scarp accordingly to the ISRM standards for outcropping joints [61]. Shear strength values obtained from direct shear tests showed a strong connection with the surface morphological features. According to the Mohr–Coulomb criterion, a value of peak friction angle of 35° with null cohesion was obtained. Multiple shear loading cycles were also applied to each specimen, obtaining a residual friction angle of 25°. According to the ISRM Suggested Methods [61,62], normal and shear joint stiffness range, respectively, from 1.5 GPa/m to 4.08 GPa/m and from 1.01 GPa/m to 1.45 GPa/m, consistent with the morphological features of joint surfaces.

2.2. Geomechanical Model

2.2.1. Modelling Approach

Numerical analysis of the Piuro rock slope was performed using the finite difference (FDM) code FLAC3D (version 7.0—[63,64,65]), suited to analyze the hydro-mechanical behavior of geomaterials with a three-dimensional approach.
In the adopted code, the slope is modeled as a continuum medium, and the domain is discretized by a continuous grid, where each zone behaves according to an assigned linear or nonlinear constitutive law. Due to its explicit finite volume formulation, the code is able to deal with large strains (e.g., large displacements) and capture instabilities including cases of yield and failure over large areas or total collapse. Moreover, using interfaces, the software can also simulate discontinuities such as faults and singular geological elements. Complex geometries can be easily modeled, allowing the simulation of sliding along weak surfaces and the evolution of deformations over time. Different authors ([63,64,65]) clearly showed the potential for using continuum FDM codes to simulate stress distributions in rock slopes, to investigate mechanisms of high-mountain deformation, and landslide formation. FLAC3D allows modeling of seepage motion through a permeable medium, taking into account the fluid–solid interaction, or HM coupling, in which variations in pore pressure induce variations in effective stresses and vice versa (two-way coupling).
In this work, the stress–strain evolution of the Piuro slope is analyzed by including its geological complexity represented by the existence of singular structural elements as the Gruf Line. Moreover, the development of failures and zones of high deformation induced by rainfall events is analyzed through a coupled HM analysis. In the above outlined framework, this work aims at evaluating if the geological setting of the slope could constitute a significant preparatory factor to the 1618 event and assessing if its triggering factor could be represented by a heavy rainfall event.
The adopted 3D modelling strategy is outlined below (Section 2.2.2, Section 2.2.3 and Section 2.2.4).

2.2.2. Geomechanical Conceptual Model

The model domain develops along the south slope of the Bregaglia Valley. It extends from Prosto to Santa Croce villages to the north and from the Corna di Garzonè peak to the Schiesone Valley to the south (Figure 1b). It includes Bregaglia Valley with Mera River, Aurosina Valley with Aurosina River, and Schiesone Valley with Schiesone River. Domain borders were placed far enough from the area of interest to avoid mechanical boundary effects (Figure 1b). The base of the model has a rectangular shape with a short side (the E-W side, parallel to the Bregaglia Valley) of 3600 m in length and the long side (the S-N side, perpendicular to the Bregaglia Valley) of 4200 m. It covers an area of 15,768,800 m2 calculated on the topographical surface. The highest elevation of the model is 2385 m a.s.l., in correspondence of the Corna di Garzonè peak, and the lower one is 364 m a.s.l., in correspondence of the Prosto Village along the Mera River.
Considering the geological complexity of the investigated slope (Section 2.1.1), the definition of the conceptual geomechanical model required a number of steps. The first one involved the reconstruction of the topography prior to the 1618 landslide event. This is based on the 2015 digital terrain model of the Lombardy Region (5 m of resolution), modified by reproducing the pre-failure topography conditions, considering the volumes of the failed rock mass, and assuming a continuity with the lateral slopes. Considering that the aim of this work is to analyze the mechanisms of the 1618 failure, only the portion of the slope representing its detachment zone was reconstructed. This is considered acceptable, since the morphology of the valley bottom is not expected to affect the stress–strain evolution in the upper part of the slope where the slope failure occurred.
A second step included the three-dimensional reconstruction of the geological elements outcropping along the slope, using the software Geomodeller (Version 3, [66]). Starting from geological maps (CROP project, [46]), it was possible to define the 3D geology by considering orientation data measured along the slope and their relationships with the topography (Figure 4a).
Planar elements such as faults and tectonic lineaments were then exported from Geomodeller and imported as surface elements in the meshing tool Rhinoceros (version 6.0, [67]). Here, through Boolean operations between the topographical surface and geological planar elements, the blocks representing the different tectonic units were created: Chiavenna unit, Gruf unit, and Tambò unit. These blocks were then introduced in a subsequent step in FLAC3D as separate units with a finite volume (Figure 4b). Blocks were discretized into a finite-difference grid by the definition of mixed hexahedral zones (Figure 4c). A maximum zone size of 80 m was set, letting the software automatically create a best-fitting grid considering the input morphology, allowing a significant reduction in computation time. Given the overall extension of the model domain, resulting in a side length of over 3 km, a zone size of 80 m is deemed sufficient to capture the general behavior of the slope. A total number of 121,228 zones were thus created resulting in 866,260 nodes.
Contact between blocks representing the geological separation between tectonic units were set as mechanical interfaces, which can deform following assigned strength and stiffness parameters (Table 1). On the other hand, adjacent zones that are not characterized by geological evidence of the presence of a fault (dashed line in Figure 1d) were merged using the “attaching” tool, defining a single coeval body.
Boundary conditions of fixed zero velocity are specified along the bottom boundary of the model domain, and fixed normal zero velocity was set along the side boundaries (Figure 4d).
As the model was created and the boundary conditions were defined, mechanical properties were introduced using the Hoek–Brown failure criterion [68]. Rock mass strength parameters were calculated by applying the GSI approach considering results from geomechanical surveys and laboratory tests (Section 2.1.4). Hoek–Brown criterion is described by the law:
σ 1 = σ 3 + σ c i ( m b σ 3 σ c i + s ) a
where σ1 is the maximum principal stress at peak of deformation; σ3 is the minimum principal stress; σci is the uniaxial compressive strength of intact rock; mb, s, and a are material constants that can be related to the geological strength index and rock damage [68]; the resulting parameters estimated for the study area are presented in Table 1. Two different mechanical property scenarios were calculated considering the measured maximum and minimum values. For interfaces, the Mohr–Coulomb criterion was adopted, and relevant strength and deformability parameters were defined from laboratory measurements.
Considering that the main aim of this work is to evaluate the role of geological features along the slope as preparatory factors for the 1618 landslide event, the development of a landslide body was not forced in the model by artificially introducing a sliding surface.

2.2.3. Hydrogeological Conceptual Model

A 3D transient groundwater flow simulation was carried out using the FLAC3D software in order to simulate the triggering rainfall event. Due to the absence of direct piezometric measurements in the slope, some hydrogeological assumptions were made. The basal water table was introduced accounting for the presence of the Mera, Aurosina, and Schiesone Rivers flowing on the bottom of the valleys surrounding the Piuro slope. The resulting basal piezometric level would cross the slope of interest only on its lower part, laying largely below the detected slip failure surface of the studied landslide (Figure 4e). This level represents the starting condition for the subsequent transient hydrogeological analysis.
The principal assumption in the hydrogeological model is that the slope is only recharged by water infiltrating from its surface during rainfall events. Deep groundwater recharge is not considered in this model. This assumption was necessary as lateral and deep flow contributions are difficult to estimate in the absence of measured data. As the aim of this work is to analyze the failure mechanisms developed in the subsurface of the slope, this assumption is not considered to exert a significant influence in the magnitude of pore pressures at shallow depths. Groundwater flow modelling is used, in this context, to reproduce the pore pressure evolution over space and time, without studying the groundwater flow system in detail.
Rock mass’ principal hydraulic conductivities were calculated by defining the permeability tensor, considering joint orientation, JRC, aperture, and fracture frequency of each discontinuity set [69]. A value of equivalent hydraulic conductivity keq = 1.51 × 10−7 m/s was calculated considering the collected data from geomechanical surveys (Section 2.1.3). Even if a small difference was found between the Chiavenna (1.75 × 10−7 m/s) and Gruf unit (1.27 × 10−7 m/s), as a first step of the analysis, a homogenous hydrogeological unit was introduced, in order to reduce computational costs. The material was assumed to be isotropic in agreement with field observations that showed a fracture network composed of a system of discontinuities orthogonal to each other (Figure 2c). Moreover, in this model, the interfaces were assumed to be fully permeable.
The definition of the rockslide triggering factor involved the analysis of the rainfall regimes. According to historical notes, the 1618 failure was preceded by a heavy rainfall event that persisted during the entire week before the landslide occurred. However, no measured data are available. To identify a possible rainfall triggering value, meteorological data relative to the most significant landslide events that affected the Valchiavenna and Valtellina region in recent decades were collected. They were related to the rainfall probability lines calculated for the Piuro area based on data collected by ARPA’s (Regional Agency for Environmental Protection) measurement stations (http://iris.arpalombardia.it/, accessed on 1 November 2021; Figure 4f). This method is based on the current meteorological data set and assumes that the pluviometric regime did not vary during the past centuries. Although this can lead to significant errors when forecasting and early-warning scenarios are analyzed, in this paper, the method is only applied to find reasonable rainfall data with which to perform the hydromechanical analysis.
Based on the current meteorological data, a hypothesis coincident with a return period of 200 years, corresponding to a duration of 5 days, and total accumulated water of 345 mm, was made. This trigger rainfall value was divided into periods of constant rainfall intensity, and a vertical infiltration value of 8 × 10−7 m/s was calculated assuming the absence of surface runoff. The infiltration function evaluated over time represents the input data for the transient hydromechanical analysis, in which the hydrogeological boundary conditions are represented by (Figure 4e):
-
Function over time of vertical water infiltration along slope surfaces (8 × 10−7 m/s for 432,000 s);
-
Zero pore pressure along the Piuro Valley floor, Aurosina Valley, and Schiesone Valley, simulating the presence of streams;
-
No flow along the sides and at the base of the model.

2.2.4. Modelling Procedure

The simulation was performed starting from the reproduction of mechanical initial state conditions, followed by an elasto-plastic hydro-mechanical analysis. Given the complexity of the geometries and the large number of elements in the model, the initial elastic stress field due to the gravity load and topography constraints was calculated by a mechanical initialization until force-equilibrium was reached in dry conditions (step 1). In this step, possible tectonic forces related to the alpine dynamics are not considered, as their difficult estimation would add excessive uncertainties to the model. Once the initialization procedure was completed, the effect of groundwater in the effective stress state was evaluated introducing a static piezometric level, determined considering the local ordinary hydrogeological regime (step 2).
The effective stress state distribution resulting from step 2 was used as the basis for the subsequent elasto-plastic calculation stage where, once the elastic displacements and velocities (deemed meaningless) were set to zero, the global equilibrium state was recalculated (step 3).
A lowering of strength and deformability properties, representing the mechanical degradation of the rock masses, was then established by reducing the GSI index (and consequently the Hoek–Brown strength parameters) from Scenario 1 to Scenario 2 (Section 2.2.2, Table 1) consistently with field observations, and elasto-plastic equilibrium was recalculated (step 4). Next, the effects of a triggering rainfall event were simulated using a fully coupled hydro-mechanical analysis. Rainfall and hydrogeological conditions were reproduced by a transient groundwater flow analysis, specifying a vertical infiltration along the slope (Section 2.2.3). The hydromechanical formulation was solved by the FLAC3D code using an explicit finite difference scheme with an automatically computed timestep of 18 s (step 5).
Following the concept of progressive failure mechanism, steps 1 to 4 aim at reproducing the preparatory stages leading the system to a progressive mechanical degradation. This causes a general strength reduction and an increase in the slope deformations. In the last step (step 5), the introduction of rainfall infiltration represents the ultimate collapse triggering factor.

3. Results

The output of the above outlined numerical analysis is evaluated in terms of stress–strain field redistribution in the rock mass domain and the development of plastic strain and failures. The impact of groundwater circulation in the stress–strain field is assessed by comparing results between different steps of the analysis. To evaluate localized stress changes and possible plastic strain localization, some monitoring points were defined at different depths along the slope where the failure zone of the 1618 event was located. Different 2D sections with N-S direction orthogonal to the valley axis were analyzed.
Following the modelling procedure presented in Section 2.2.4 at the first initialization steps (1–2), it was possible to reconstruct the stress states along the slope given by gravity, considering topographic constraints. The pore pressures are zero in correspondence with valley bottoms and gradually increase with depth, consistent with the water table boundary conditions (Figure 5a).
Figure 5b shows the vertical effective stress contours ( σ Z Z ′ ) and the orientation of the stress tensor. It can be observed that the major principal stresses ( σ 1 ′ ) are directed according to the maximum slope gradient and have an orientation parallel to the slope surface with an inclination angle of about 40 degrees. Their inclination decreases rapidly in the valley floor becoming perpendicular to the valley axis.
The distribution and magnitude of the simulated total displacements are consistent with the slope morphology: their vertical component (of the order of 1 m) is maximum in the upper portion of the slope, while the horizontal one (of the order of 0.9 m) is largest in its central part (Figure 5c). At step 3, using large strength parameters for the rock mass and with standard hydrogeological conditions, no failure conditions are reached, neither within rock mass elements nor along geological interfaces (Figure 6a–c).
The reduction of geomechanical properties (step 4) induces a significant increase in the number of yielded elements and a slight increase in the shear strain modulus. An area of large displacements (with maximum values of 1 m) develops along the N-S lineament at an altitude of about 1400 m a.s.l., close to the Alpe Prato del Conte locality. Consistently, plastic shear and tensile failures begin to develop in the same area up to a maximum depth of 200 m from the slope surface (Figure 6e). Even if an instability attitude is evident along this portion of the slope, a critical condition is not yet reached at this stage.
Finally, the introduction of vertical water infiltration with a fully coupled transient HM analysis (step 5) leads to the development of localized excess pore pressures along the slope. The simulated water flow moves toward the base of the slope, both northward (in the direction of Piuro) and southward (in the direction of the Schiesone Valley), consistent with the hydraulic conductivity values introduced in the model. Pore pressure increase occurs at the toe of the slope due to an accumulation of water and a consequent rise in the groundwater level. Significant pore pressure increase occurs also in correspondence of the Alpe Prato del Conte locality, where gentler dipping slopes allow water accumulation. In this portion, a significant decrease in the effective stresses until a depth of 300 m was observed (see Figure 6g compared to Figure 6d). This was sufficient to generate a large increase in shear and tensile straining leading to failure, as is apparent by comparing Figure 6h with Figure 6e. At the end of the simulated rainfall event, tensile zones are identified upstream from the Alpe Prato del Conte locality toward the top of the slope, whereas shear plastic zones are present at its base.
Focusing on the top portion of the slope, a surface along which shear strains concentrate is observed to develop during the HM simulation (Figure 6i). It extends from elevations of 1300 m up to 1600 m a.s.l. and reaches a maximum depth of 150 m.
In terms of total displacements (the resultant of the modulus of the 3D displacement vectors), the simulation results in large values localized along the N-S lineament at an altitude of about 1400 m a.s.l., in correspondence to the 1618 failure area (Figure 7a,b). Maximum values up to 5 m are reached at the end of the transient HM analysis.
Studying the evolution of the displacement values recorded by the monitoring points located in the failure area of the 1618 event, it can be observed that during the seepage process plastic conditions are reached. This is highlighted by the sudden rise in shear strain rate, indicating the achievement of irreversible conditions. This is most evident for the points located in the surroundings of the main failure zone of the slope (A, B, C points in Figure 7c) and is less evident in the upper part where the deformations are markedly smaller (D point in Figure 7c).
The maximum shear strain and total displacement distribution clearly show the presence of a critical, composite sliding surface approximately corresponding to the observed one.

4. Discussion

A hydro-mechanical analysis with a 3D numerical approach was presented, exploring the stress–strain distribution along the Piuro slope with a complex 3D geology and the effects of a heavy rainfall event as a possible triggering factor for the 1618 collapse.
By comparing results between different steps of the analysis, the role of pore pressure increments in the stress–strain evolution of rock-slopes was highlighted, demonstrating that induced damage and slope displacements are strongly enhanced in the presence of HM couplings.
Focusing on the modeling approach, steps 1 to 4 represent the preparatory factors leading the system to a gradual mechanical degradation. This causes a general strength reduction and an increase in slope deformations. In the Alpine environment, this is generally linked to glacial loading and unloading cycles, and hydro- and thermo-mechanical fatigue [18]. Considering the purposes of the present analysis, the weakening of rock masses was not numerically simulated in detail but was enforced by introducing as model parameters the weakest values of mechanical parameters among those measured in the study area. At the end of step 4 and before the introduction of the triggering factor, plastic shear strains and resulting displacements are concentrated along the N-S lineament at an altitude of about 1400 m a.s.l., close to the Alpe Prato del Conte locality. Even if collapse conditions are not reached, preparation toward instability is quite evident.
These observations clearly highlight how the N-S geological element plays a significant role as a predisposing factor to gravitational instability along the analyzed slope, in total agreement with previous studies conducted for the Piuro landslide [2,3]. The evaluation of the influence of a composite geometry in the stress–strain field was possible thanks to the use of a 3D modeling approach, which allowed the introduction of the complex geological structure characterizing the southern slope of the Bregaglia Valley. This confirms the observations of previous authors, who underlined the importance of including 3D topography when analyzing the stress–strain evolution of rock slopes and complex landslides in the Alpine environment (e.g., [45]). The development of pore pressures and the distribution of localized stresses caused by 3D topographic constraints are not negligible.
The considered rainfall scenario was sufficient to generate an increase in pore pressures and induce a significant increment of deformations and displacements. Although the actual magnitude of the rainfall event is unknown, the assumed value for this work is consistent with the current measurements in the area, and it allowed a demonstration of the role of heavy rainfall as a triggering factor for the 1618 event, in agreement with the historical writings.
By comparing modelling outputs with the observations resulting from geological and geomorphological field surveys, a verification on the simulated geometry and location of the failure scar can be carried out.
Simulation results are in accordance with previous studies that identified the failure scar in correspondence of the Alpe Prato del Conte locality. At the end of the transient HM analysis, maximum total displacements are concentrated along the N-S geological element that cut the Gruf Line. The highest magnitude is recorded at an elevation of 1500 m a.s.l. and at a depth of 100 m, defining a cluster of highly deformed elements a few meters east of the Alpe Prato del Conte plateau. Displacements of lower magnitudes are also present upstream, moving toward the Mottaccio Peak. This is in agreement with geomorphological mapping that detected the presence of a main scarp at an elevation of about 1500 m a.s.l. and secondary and minor scarps at larger altitude (Section 2.1.2). Moreover, the evolution of strains and the development of plastic shear and tensile failures are in agreement with the state of the rock masses outcropping along the slope as analyzed by geomechanical surveys (Section 2.1.3). The development of zones under dilatation and elements reaching tensile failure is consistent with the presence of disarticulated rock masses along the top portion of the slope and is also in agreement with the development of regions of stress release as observed at the main scarp, marked by the presence of trenches and counterscarps.
Regarding the dynamics of the event, field surveys and the nature of the landslide deposit suggest an involvement of both rock and glacial materials (mixed deposits made by soil and cobblestones). Numerical simulations showed how the initiation of the instability should have occurred along the geological bedrock. However, considering the geomorphological framework of the failure area and the materials outcropping along the slope, the sliding mass must have involved glacial deposits that covered the Alpe Prato del Conte terrace and glacial terraces located downstream during the run-off of the failed mass. This is confirmed by field observations in the detachment zone, where rock scarps interrupt flat morphologies made by glacial deposits as well as the morphological terrace of Pradella di Piuro and Alpe Moscone, which are clearly cut by the landslide deposit. Since this work mainly focused on reproducing the preparation and triggering of the main deep-seated sliding mechanism, the adopted model did not include the soil material covering the bedrock. Future work could explore the subsequent dynamic evolution of the landslide involving both the bedrock and soil cover. To this end, a hybrid modelling approach following the continuum–discrete-distinct method could be explored (e.g., [70,71]).
Analyzing the trend of deformations and the location of the slip surface, the volumes of the failed mass simulated by the model amount to approximately 7 Mm3. Considering the material taken along the downstream path, the material deposited along the valley, and the volumetric expansion of the material after failure (around 30%), values of about 10 Mm3 can be estimated. These are higher volume values than those suggested by [3], based on the stratigraphical reconstruction of the deposit on the Piuro plain. However, it must be observed that the grid size used for domain discretization is 80 m. For a more accurate assessment of the sliding volumes, it is necessary to decrease the grid size to lower values. This will lead to an increase in computational costs that must be addressed especially during the fully coupled HM analysis. The assessment of failed volumes was certainly influenced by the presence of discontinuity systems, whose planes represented release surfaces, as shown in Section 2.1.3. In this regard, future development of the analysis could also explore the introduction of the discontinuity network detected with geomechanical surveys and its influence in the failing mechanisms using a discrete (as opposed to continuum) modelling approach.

5. Conclusions

In this work, an accurate geomorphological and geomechanical characterization along the Piuro slope was first carried out. This led to the recognition of principal elements related to the failure event, identifying main release scarps, secondary scarps, and traction trenches.
By accounting for the complex geological framework of the slope, a 3D numerical model was implemented allowing analysis of the stress–strain evolution of the slope. Starting from ordinary hydrogeological conditions and defining two mechanical steps, the stress–strain field of the slope was simulated. The predisposition to instability related to the presence of the tectonic contact between the Chiavenna unit and the Gruf unit is highlighted by the strain localization and the presence of zones reaching shear and tensile failure across the N-S geological element.
Then, a fully coupled hydromechanical elastoplastic 3D analysis was conducted in order to back analyze the 1618 Piuro landslide by considering the vertical infiltration process related to a heavy rainfall event as the triggering factor, as indicated by historical documents.
To identify a possible rainfall triggering value, meteorological data relevant to the most significant landslide events that affected the Valchiavenna and Valtellina regions in recent decades were collected. A hypothesis coincident with a return period of 200 years corresponding to a rain duration of 5 days and total accumulated water of 300 mm was made. The resulting displacements and the development of a deep shear–strain localization zone are in agreement with the evidence of the historical collapse event, clearly defining a preferential region for the development of a failure zone.
This work clearly shows the importance of including three-dimensional features when analyzing slope stress–strain evolution, especially when the geological framework is particularly complex, as is the case for many landslide events in the Alpine region. In fact, slope morphology strongly influences the distribution of stresses and the development of localized excess pore pressures induced by topographic constraints. Through numerical modelling, this study corroborates observations made by previous authors about the location of the Piuro landslide detachment zone, the preparatory role of geological elements, as well as the triggering role represented by a rainfall event.
This work is part of the Interreg IT-CH Project A.M.AL.PI.18, which aims to encourage an innovative strategy for the promotion of tourism in Alpine areas, including through the creation of a cross-border geo-cultural trail from the Maloja Pass to the Gotthard Pass (Bregaglia–Valchiavenna–Moesa–Ticino region), linking sites that have undergone major geomorphological and anthropogenic changes due to the occurrence of landslides of great social impact. The Piuro landslide is the main case history that inspired the project. The rigorous scientific approach was chosen to help raise awareness of natural hazards and promote a culture of risk and resilience in mountainous areas.

Author Contributions

Conceptualization: A.M., T.A., and F.C.; Methodology: A.M., T.A., and F.C.; Formal analysis and investigation: A.M.; Writing—original draft preparation: A.M.; Writing—review and editing: A.M., T.A., and F.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research has been carried out in the framework of the European Regional Development Fund, under the Interreg V-A Italy-Switzerland Cooperation Program, among the activities of the Project ID 594274 A.M.AL.PI.18 ‘Alpi in Movimento, Movimento nelle Alpi. Piuro 1618-2018′ (https://progetti.interreg-italiasvizzera.eu/it/b/78/alpiinmovimentomovimentonellealpipiuro, accessed on 1 November 2021) and the Doctoral Program in Earth Sciences of the University of Milan.

Data Availability Statement

All relevant data are published in the manuscript text and referenced literature. Meteorological data used in this work are freely accessible at https://www.arpalombardia.it/, accessed on 1 November 2021.

Acknowledgments

Authors would like to acknowledge Itasca International, Inc. for providing the FLAC3D code license through the Itasca Educational Partnership (IEP) Research Program agreement. We also acknowledge Marco Perfido, technician of the Engineering Geology Laboratory of the University of Milan and Enrico Pigazzi for the field activities support.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Scaramellini, G.; Kahl, G.; Falappi, G.P. La Frana di Piuro del 1618: Storia e Immagini di una Rovina; Associazione italo-svizzera per gli scavi di Piuro: Borgonuovo, Italy, 1988. [Google Scholar]
  2. Scaramellini, G.; Kahl, G.; Falappi, G.P. La Frana di Piuro del 1618: Storia e Immagini di una Rovina, 2nd ed.; Associazione italo-svizzera per gli scavi di Piuro: Borgonuovo, Italy, 1995. [Google Scholar]
  3. Pigazzi, E.; Bersezio, R.; Morcioni, A.; Tantardini, D.; Apuani, T. Geology of the area of the Piuro 1618 event (Val Bregaglia, Italian Central Alps): The setting of a catastrophic historical landslide. J. Maps 2022, 18, 342–351. [Google Scholar] [CrossRef]
  4. Mann, M.; Zhang, Z.; Rutherford, S.; Bradley, R.; Hughes, M.; Shindell, D.; Ammann, C.; Faluvegi, G.; Ni, F. Global signatures and dynamical origins of the Little Ice Age and Medieval Climate Anomaly. Science 2009, 326, 1256–1260. [Google Scholar] [CrossRef] [PubMed]
  5. Grove, A.T. The little ice age and its geomorphological consequences in mediterranean Europe. Clim. Change 2001, 48, 121–136. [Google Scholar] [CrossRef]
  6. De Pedrini, A.; Ambrosi, C.; Scapozza, C. The 1513 Monte Crenone rock avalanche: Numerical model and geomorphological analysis. Geogr. Helv. 2022, 77, 21–37. [Google Scholar] [CrossRef]
  7. Scapozza, C.; Tognacca, C.; Ambrosi, C.; Seno, S. 20 maggio 1515: La “Buzza” che impressionò l’Europa. Boll. Soc. Ticin. Sci. Nat. 2015, 103, 78–88. [Google Scholar]
  8. Stoffel, M.; Beniston, M. On the incidence of debris flows from the early Little Ice Age to a future greenhouse climate: A case study from the Swiss Alps. Geophys. Res. Lett. 2006, 33, L16404. [Google Scholar] [CrossRef]
  9. Maraun, D.; Knevels, R.; Mishra, A.N.; Truhetz, H.; Bevacqua, E.; Proske, H.; Zappa, G.; Brenning, A.; Petschko, H.; Schaffer, A.; et al. A severe landslide event in the Alpine foreland under possible future climate and land-use changes. Commun. Earth Environ. 2022, 3, 87. [Google Scholar] [CrossRef]
  10. Crosta, G.; Chen, H.; Lee, C. Replay of the 1987 Val Pola Landslide, Italian Alps. Geomorphology 2004, 60, 127–146. [Google Scholar] [CrossRef]
  11. Barla, G.; Barla, M. Investigation and modelling of the Brenva Glacier rock avalanche on the Mount Blanc Range. In Proceedings of the ISRM Regional Symposium Eurock, Espoo, Finland, 4–7 June 2001; pp. 35–40. [Google Scholar]
  12. Loew, S.; Gschwind, S.; Gischig, V.; Keller-Signer, A.; Valenti, G. Monitoring and early warning of the 2012 Preonzo catastrophic rockslope failure. Landslides 2016, 14, 141–154. [Google Scholar] [CrossRef]
  13. Morcioni, A.; Bajni, G.; Apuani, T. The Cimaganda Rockslide (Italian Alps): Geomechanical characterization and hydro-mechanical numerical modelling. Rend. Online Soc. Geol. Ital. 2020, 52, 40–46. [Google Scholar] [CrossRef]
  14. Walter, F.; Amann, F.; Kos, A.; Kenner, R.; Phillips, M.; de Preux, A.; Huss, M.; Tognacca, C.; Clinton, J.; Diehl, T.; et al. Direct observations of a three million cubic meter rock-slope collapse with almost immediate initiation of ensuing debris flows. Geomorphology 2020, 351, 106933. [Google Scholar] [CrossRef]
  15. Carlà, T.; Gigli, G.; Lombardi, L.; Nocentini, M.; Casagli, N. Monitoring and analysis of the exceptional displacements affecting debris at the top of a highly disaggregated rockslide. Eng. Geol. 2021, 294, 106345. [Google Scholar] [CrossRef]
  16. Preisig, G.; Eberhardt, E.; Smithyman, M.; Preh, A.; Bonzanigo, L. Hydromechanical Rock Mass Fatigue in Deep-Seated Landslides Accompanying Seasonal Variations in Pore Pressures. Rock Mech. Rock Eng. 2016, 49, 2333–2351. [Google Scholar] [CrossRef]
  17. Manconi, A.; Giordan, D. Landslide early warning based on failure forecast models: The example of the Mt. de La Saxe rockslide, northern Italy. Nat. Hazards Earth Syst. Sci. 2015, 15, 1639–1644. [Google Scholar] [CrossRef]
  18. Eberhardt, E. Twenty-ninth Canadian Geotechnical Colloquium: The role of advanced numerical methods and geotechnical field measurements in understanding complex deep-seated rock slope failure mechanisms. Can. Geotech. J. 2008, 45, 484–510. [Google Scholar] [CrossRef]
  19. Pedrazzini, A.; Jaboyedoff, M.; Loye, A.; Derron, M.-H. From deep seated slope deformation to rock avalanche: Destabilization and transportation models of the Sierre landslide (Switzerland). Tectonophysics 2013, 605, 149–168. [Google Scholar] [CrossRef]
  20. Leith, K.; Moore, J.R.; Amann, F.; Loew, S. Subglacial extensional fracture development and implications for Alpine Valley evolution. J. Geophys. Res. Earth Surf. 2014, 119, 62–81. [Google Scholar] [CrossRef]
  21. Bonzanigo, L.; Oppizzi, P.; Tornaghi, M.; Uggeri, U. Hydrodynamics and rheology: Key factors in mechanisms of large landslides. In Proceedings of the 2006 ECI Conference on Geohazards, Lillehammer, Norway, 18–21 June 2006. [Google Scholar]
  22. Calista, M.; Miccadei, E.; Piacentini, T.; Sciarra, N. Morphostructural, Meteorological and Seismic Factors Controlling Landslides in Weak Rocks: The Case Studies of Castelnuovo and Ponzano (North East Abruzzo, Central Italy). Geosciences 2019, 9, 122. [Google Scholar] [CrossRef]
  23. Nguyen, L.C.; Van Tien, P.; Do, T.-N. Deep-seated rainfall-induced landslides on a new expressway: A case study in Vietnam. Landslides 2019, 17, 395–407. [Google Scholar] [CrossRef]
  24. Gischig, V.S.; Moore, J.; Evans, K.F.; Amann, F.; Loew, S. Thermomechanical forcing of deep rock slope deformation: 1. Conceptual study of a simplified slope. J. Geophys. Res. Atmos. 2011, 116, 1–18. [Google Scholar] [CrossRef]
  25. Morcioni, A.; Apuani, T.; Cecinato, F. The Role of Temperature in the Stress–Strain Evolution of Alpine Rock-Slopes: Thermo-Mechanical Modelling of the Cimaganda Rockslide. Rock Mech. Rock Eng. 2022, 55, 2149–2172. [Google Scholar] [CrossRef]
  26. Scaringi, G.; Loche, M. A thermo-hydro-mechanical approach to soil slope stability under climate change. Geomorphology 2022, 401, 108108. [Google Scholar] [CrossRef]
  27. Grämiger, L.M.; Moore, J.R.; Gischig, V.S.; Loew, S. Thermomechanical Stresses Drive Damage of Alpine Valley Rock Walls During Repeat Glacial Cycles. J. Geophys. Res. Earth Surf. 2018, 123, 2620–2646. [Google Scholar] [CrossRef]
  28. Baroni, C.; Martino, S.; Salvatore, M.C.; Mugnozza, G.S.; Schilirò, L. Thermomechanical stress–strain numerical modelling of deglaciation since the Last Glacial Maximum in the Adamello Group (Rhaetian Alps, Italy). Geomorphology 2014, 226, 278–299. [Google Scholar] [CrossRef]
  29. Seguí, C.; Veveakis, M. Continuous assessment of landslides by measuring their basal temperature. Landslides 2021, 18, 3953–3961. [Google Scholar] [CrossRef]
  30. Seguí, C.; Rattez, H.; Veveakis, M. On the Stability of Deep-Seated Landslides. The Cases of Vaiont (Italy) and Shuping (Three Gorges Dam, China). J. Geophys. Res. Earth Surf. 2020, 125, e2019JF005203. [Google Scholar] [CrossRef]
  31. Cecinato, F.; Zervos, A.; Veveakis, E. A thermo-mechanical model for the catastrophic collapse of large landslides. Int. J. Numer. Anal. Methods Géoméch. 2010, 35, 1507–1535. [Google Scholar] [CrossRef]
  32. Veveakis, M.; Vardoulakis, I.; Di Toro, G. Thermoporomechanics of creeping landslides: The 1963 Vaiont slide, northern Italy. J. Geophys. Res. Atmos. 2007, 112, F03026. [Google Scholar] [CrossRef]
  33. Vardoulakis, I. Dynamic thermo-poro-mechanical analysis of catastrophic landslides. Geotechnique 2002, 52, 157–171. [Google Scholar] [CrossRef]
  34. Eberhardt, E.; Stead, D.; Coggan, J. Numerical analysis of initiation and progressive failure in natural rock slopes—The 1991 Randa rockslide. Int. J. Rock Mech. Min. Sci. 2004, 41, 69–87. [Google Scholar] [CrossRef]
  35. Brideau, M.-A.; Yan, M.; Stead, D. The role of tectonic damage and brittle rock fracture in the development of large rock slope failures. Geomorphology 2009, 103, 30–49. [Google Scholar] [CrossRef]
  36. Scholtès, L.; Donzé, F.-V. Modelling progressive failure in fractured rock masses using a 3D discrete element method. Int. J. Rock Mech. Min. Sci. 2012, 52, 18–30. [Google Scholar] [CrossRef]
  37. Sandøy, G.; Oppikofer, T.; Nilsen, B. Why did the 1756 Tjellefonna rockslide occur? A back-analysis of the largest historic rockslide in Norway. Geomorphology 2017, 289, 78–95. [Google Scholar] [CrossRef]
  38. Shen, H.; Klapperich, H.; Abbas, S.M.; Ibrahim, A. Slope stability analysis based on the integration of GIS and numerical simulation. Autom. Constr. 2012, 26, 46–53. [Google Scholar] [CrossRef]
  39. Li, L.; Wang, Y. Identification of failure slip surfaces for landslide risk assessment using smoothed particle hydrodynamics. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2019, 14, 91–111. [Google Scholar] [CrossRef]
  40. Liu, B.; He, K.; Han, M.; Hu, X.; Wu, T.; Wu, M.; Ma, G. Dynamic process simulation of the Xiaogangjian rockslide occurred in shattered mountain based on 3DEC and DFN. Comput. Geotech. 2021, 134, 104122. [Google Scholar] [CrossRef]
  41. Riva, F.; Agliardi, F.; Amitrano, D.; Crosta, G. Damage-based time-dependent modeling of paraglacial to postglacial progressive failure of large rock slopes. J. Geophys. Res. Earth Surf. 2018, 123, 124–141. [Google Scholar] [CrossRef]
  42. Commend, S.; Geiser, F.; Tacher, L. 3D numerical modeling of a landslide in Switzerland. Numerical Models in Geomechanics. In Proceedings of the 9th Proceedings of the International Symposium on Numerical Models in Geomechanics, NUMOG, Ottawa, ON, Canada, 25–27 August 2004; pp. 595–602. [Google Scholar] [CrossRef]
  43. Lignon, S.; Laouafa, F.; Prunier, F.; Khoa, H.; Darve, F. Hydro-mechanical modelling of landslides with a material instability criterion. Geotechnique 2009, 59, 513–524. [Google Scholar] [CrossRef]
  44. Mergili, M.; Marchesini, I.; Rossi, M.; Guzzetti, F.; Fellin, W. Spatially distributed three-dimensional slope stability modelling in a raster GIS. Geomorphology 2014, 206, 178–195. [Google Scholar] [CrossRef]
  45. Wolter, A.; Havaej, M.; Zorzi, L.; Stead, D.; Clague, J.J.; Ghirotti, M.; Genevois, R. Exploration of the kinematics of the 1963 vajont slide, Italy, using a numerical modelling toolbox. Ital. J. Eng. Geol. Environ. 2013, 6, 599–612. [Google Scholar] [CrossRef]
  46. Montrasio, A.; Sciesa, E. Carta geologica della valle Spluga ed aree adiacenti, scala 1:50.000. CNR-Prog. Strat. Crosta Profond. (CROP) Milano 1988. Università di Milano. [Google Scholar]
  47. Falappi, P. La frana di Piuro in Bregaglia del 1618: Fantasie e realtà. Quaderni grigionitaliani 2012, 81, 123–137. [Google Scholar] [CrossRef]
  48. Schmutz, H. Der Mafit-Ultramafit-Komplex zwischen Chiavenna und Val Bondasca. Beitr. Geol. Karte Schweiz. N.F. 1976, 149, 73. [Google Scholar]
  49. Tibaldi, A.; Pasquarè, F. Quaternary deformations along the ‘Engadine–Gruf tectonic system’, Swiss–Italian Alps. J. Quat. Sci. 2009, 22, 311–320. [Google Scholar] [CrossRef]
  50. Trümpy, R. The Engadine line: A sinistral wrench fault in the Central Alps. Mem. Geol. Soc. China 1977, 2, 1. [Google Scholar]
  51. Wenk, H.-R. Brittle-ductile Transition Zone in the Northern Bergell Alps. Int. J. Earth Sci. 1984, 73, 419–431. [Google Scholar] [CrossRef]
  52. Albini, P.; Bellani, A.; Stucchi, M. Terremoti e frane nelle Alpi Centrali. Atti Del 1988, 7, 129–146. [Google Scholar]
  53. ISMES. Studi Sismici in Alta Valtellina; I quaderni dell’ISMES 336: Bergamo, Italy, 1994. [Google Scholar]
  54. Galli, A. Tectono-Metamorphic Evolution of the Gruf complex (Swiss and Italian Central Alps). Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2010. [Google Scholar]
  55. Tantardini, D.; Stevenazzi, S.; Apuani, T. The Last Glaciation in Valchiavenna (Italian Alps): Maximum ice elevation data and recessional glacial deposits and landforms. Ital. J. Geosci. 2022, 141, 259–277. [Google Scholar] [CrossRef]
  56. ISRM—International society for Rock Mechanics. Rock Characterization, Testing and Monitoring; ISRM Suggested Methods: Pergamon, London, 1981. [Google Scholar]
  57. Bieniawski, Z.T. Engineering Rock Mass Classification—Cap. 4; Butterworth-Heinemann: Boston, MA, USA, 1989; pp. 51–69. [Google Scholar]
  58. Hoek, E.; Marinos, P. Predicting tunnel squeezing problems in weak heterogeneous rock masses. Tunn. Tunn. Int. 2000, 32, 45–51. [Google Scholar]
  59. ASTM D7012-14; Standard Test Methods for Compressive Strength and Elastic Moduli of Intact Rock Core Specimens under Varying States of Stress and Temperatures. ASTM International: West Conshohocken, PA, USA, 2014. [CrossRef]
  60. ASTM D5607-08; Standard Test Method for Performing Laboratory Direct Shear Strength Tests of Rock Specimens Under Constant Normal Force. ASTM International: West Conshohocken, PA, USA, 2008. [CrossRef]
  61. ISRM—International society for Rock Mechanics. The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007–2014; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
  62. Kulatilake, P.H.S.W.; Shreedharan, S.; Sherizadeh, T.; Shu, B.; Xing, Y.; He, P. Laboratory Estimation of Rock Joint Stiffness and Frictional Parameters. Geotech. Geol. Eng. 2016, 34, 1723–1735. [Google Scholar] [CrossRef]
  63. Itasca. FLAC3D—Fast Lagrangian Analysis of Continua; Version 7.0, User’s Manual; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2019. [Google Scholar]
  64. de Ojeda, P.S.; Sanz, E.; Galindo, R. Historical reconstruction and evolution of the large landslide of Inza (Navarra, Spain). Nat. Hazards 2021, 109, 2095–2126. [Google Scholar] [CrossRef]
  65. Zabuski, L. Three-Dimensional Analysis of a Landslide Process on a Slope in Carpathian Flysch. Arch. Hydro-Eng. Environ. Mech. 2019, 66, 27–45. [Google Scholar] [CrossRef]
  66. Intrepid Geophysics. Geomodeller; Version 3, User’s Manual; Intrepid Geophysics, Inc.: Brightorn, UK, 2014. [Google Scholar]
  67. McNeel, R. Rhinoceros 3D; Version 6.0; Robert McNeel & Associates: Seattle, WA, USA, 2010. [Google Scholar]
  68. Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek-Brown failure criterion—2002 edition. In Proceedings of the NARMS-TAC Conference, Toronto, ON, Canada, 7–10 July 2002; pp. 267–273. [Google Scholar]
  69. Lotti, F.; Baiocchi, A.; D’onofrio, S.; Piscopo, V. Hydrogeological site characterization of marly-silici-calcareous rocks through surveys of discontinuities and pumping tests. Acque Sotter. Ital. J. Groundw. 2012, 1, 27–36. [Google Scholar] [CrossRef] [Green Version]
  70. Ma, Y.; Sheng, Q.; Zhang, G.; Cui, Z. A 3D Discrete-Continuum Coupling Approach for Investigating the Deformation and Failure Mechanism of Tunnels across an Active Fault: A Case Study of Xianglushan Tunnel. Appl. Sci. 2019, 9, 2318. [Google Scholar] [CrossRef]
  71. Pu, S.; Yu, T.; Ye, L.; Liao, H.; Fang, Y.; Yao, Z.; Wang, J. Study on Instability Mechanism and Support Scheme of the Tunnel Face in Carbonaceous Phyllite Stratum under High Geo-Stress. Adv. Civ. Eng. 2022, 2022, 3870227. [Google Scholar] [CrossRef]
Geosciences 13 00049 g002 550
Figure 2. (a) Photo of the Piuro landslide as seen from the opposite slope. Failure, sliding and deposit zones are highlighted; (b) Geomorphological and geological features of the 1618 failure area; (c) Geomechanical features of the study area. Lower hemisphere stereographic projection of the main discontinuity sets. Joint orientation is expressed by dip direction/dip.
Figure 2. (a) Photo of the Piuro landslide as seen from the opposite slope. Failure, sliding and deposit zones are highlighted; (b) Geomorphological and geological features of the 1618 failure area; (c) Geomechanical features of the study area. Lower hemisphere stereographic projection of the main discontinuity sets. Joint orientation is expressed by dip direction/dip.
Geosciences 13 00049 g002
Geosciences 13 00049 g003 550
Figure 3. (a–c) Rock masses outcropping along the slope. Two main discontinuity sets are highlighted with different colors—also plotted on the stereographic projection of Figure 2c (lower hemisphere); (d) Traction trenches outcropping at Alpe Prato del Conte locality; (e) Landslide deposit outcropping in the sliding zone along the slope; (f) Aerial view of the landslide deposit on which the new village of Piuro stands.
Figure 3. (a–c) Rock masses outcropping along the slope. Two main discontinuity sets are highlighted with different colors—also plotted on the stereographic projection of Figure 2c (lower hemisphere); (d) Traction trenches outcropping at Alpe Prato del Conte locality; (e) Landslide deposit outcropping in the sliding zone along the slope; (f) Aerial view of the landslide deposit on which the new village of Piuro stands.
Geosciences 13 00049 g003
Geosciences 13 00049 g004 550
Figure 4. (a) 3D geological model built starting from the geological–structural features of the slope presented in Figure 1d; (b) FLAC3D model building; (c) Discretization into a finite-difference grid by the definition of hexahedral zones; (d) Boundary conditions of the mechanical model; (e) Boundary conditions of the hydrogeological model for the hydro-mechanical analysis; (f) Rainfall input of hydro-mechanical analysis. Identification of input values by evaluating rainfall scenarios in the study area.
Figure 4. (a) 3D geological model built starting from the geological–structural features of the slope presented in Figure 1d; (b) FLAC3D model building; (c) Discretization into a finite-difference grid by the definition of hexahedral zones; (d) Boundary conditions of the mechanical model; (e) Boundary conditions of the hydrogeological model for the hydro-mechanical analysis; (f) Rainfall input of hydro-mechanical analysis. Identification of input values by evaluating rainfall scenarios in the study area.
Geosciences 13 00049 g004
Geosciences 13 00049 g005 550
Figure 5. Pore pressures (a), effective stresses (b), and total displacements (c) simulated along the modelled slope at initialization phase.
Figure 5. Pore pressures (a), effective stresses (b), and total displacements (c) simulated along the modelled slope at initialization phase.
Geosciences 13 00049 g005
Geosciences 13 00049 g006 550
Figure 6. (a) Location of the 2D section showing effective stresses (d,g), zone state (b,e,h), and ZY strain increment (c,f,i) simulated for different steps of the analysis.
Figure 6. (a) Location of the 2D section showing effective stresses (d,g), zone state (b,e,h), and ZY strain increment (c,f,i) simulated for different steps of the analysis.
Geosciences 13 00049 g006
Geosciences 13 00049 g007 550
Figure 7. (a) 3D total displacements simulated at the end of the HM coupled analysis. (b) 2D total displacements along a N-S cross-section crossing the failure area. (c) Graph of measured displacements at monitoring points (Figure 6a) with mechanical cycles (defined as the number of timesteps performed).
Figure 7. (a) 3D total displacements simulated at the end of the HM coupled analysis. (b) 2D total displacements along a N-S cross-section crossing the failure area. (c) Graph of measured displacements at monitoring points (Figure 6a) with mechanical cycles (defined as the number of timesteps performed).
Geosciences 13 00049 g007
Table
Table 1. Mechanical elasto-plastic properties of blocks and interfaces. (*) Derived from laboratory tests conducted as part of the present study. (**) Derived from laboratory tests conducted by Apuani T. (previous work not published).
Table 1. Mechanical elasto-plastic properties of blocks and interfaces. (*) Derived from laboratory tests conducted as part of the present study. (**) Derived from laboratory tests conducted by Apuani T. (previous work not published).
Mechanical Properties of Blocks
Chiavenna Unit
(scenario1/scenario2)		Gruf Unit
(scenario1/scenario2)		Tambò Unit
(scenario1/scenario2)
Uniaxial Strength [MPa]180 **/175 **120 */108 *70 **/80 **
GSI70/6065/5550/50
mi26/2628/2816/16
D0.8/0.80.8/0.80.8/0.8
Ei [MPa]45,000/40,00040,000/30,00030,000/25,000
mb4.36/2.4043.486/1.9230.612/0.454
s0.0106/0.002330.00498/0.001090.000513/0.00024
a0.501/0.5030.502/0.5040.506/0.508
Poisson Ratio (υ)0.4 **/0.4 **0.3 */0.3 *0.4 **/0.4 **
Density [Kg/m3]2800 *2600 *2500*
Interfaces* (scenario 1/scenario 2)
Peak Friction Angle [°]35/28
Peak Cohesion [MPa]1/0.1
Residual Friction Angle [°]25/25
Residual Cohesion [MPa]0/0
Tensile Strength [MPa]1/0.1
Normal Stiffness [GPa m−1]5/5
Shear Stiffness [GPa m−1]1/1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Morcioni, A.; Apuani, T.; Cecinato, F. Piuro Landslide: 3D Hydromechanical Numerical Modelling of the 1618 Event. Geosciences 2023, 13, 49. https://doi.org/10.3390/geosciences13020049

AMA Style

Morcioni A, Apuani T, Cecinato F. Piuro Landslide: 3D Hydromechanical Numerical Modelling of the 1618 Event. Geosciences. 2023; 13(2):49. https://doi.org/10.3390/geosciences13020049

Chicago/Turabian Style

Morcioni, Andrea, Tiziana Apuani, and Francesco Cecinato. 2023. "Piuro Landslide: 3D Hydromechanical Numerical Modelling of the 1618 Event" Geosciences 13, no. 2: 49. https://doi.org/10.3390/geosciences13020049

APA Style

Morcioni, A., Apuani, T., & Cecinato, F. (2023). Piuro Landslide: 3D Hydromechanical Numerical Modelling of the 1618 Event. Geosciences, 13(2), 49. https://doi.org/10.3390/geosciences13020049

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop