Modelling of Urban Near-Road Atmospheric PM Concentrations Using an Artificial Neural Network Approach with Acoustic Data Input
Abstract
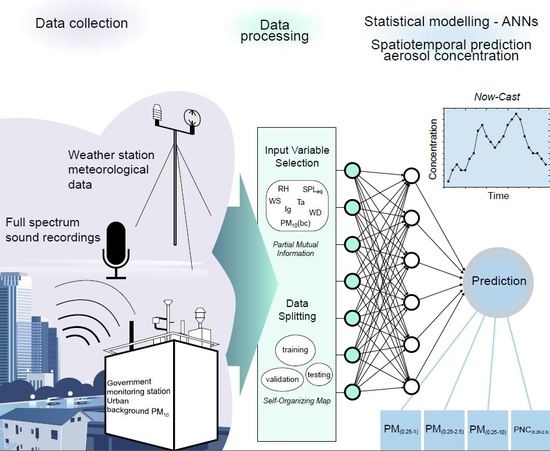
:1. Introduction
2. Materials and Methods
2.1. Research Sites
2.1.1. Aachen-Karlsgraben
2.1.2. Münster-Aasee
2.2. Artificial Neural Network Approach
2.2.1. Model Architecture—Multi-Layer Perceptron
2.2.2. Input Variable Selection
2.2.3. Data Splitting
2.2.4. Model Structure Selection
2.2.5. Model Calibration—Backpropagation Algorithm
2.3. Field Data—Collection and Pre-Processing
2.3.1. Particles
2.3.2. Acoustics
2.3.3. Meteorology
2.4. Field Data—Post-Processing
2.5. Performance Measures
3. Results
4. Discussion
4.1. Interpretation of ANN Model Results
4.2. Limitations and Future Aspects
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Babisch, W. Chronischer Lärm als Risikofaktor für den Myokardinfarkt; Ergebnisse der “NaRoMI”-Studie; Umweltbundesamt: Wien, Austria, 2004; pp. 1–159. [Google Scholar]
- Raaschou-Nielsen, O.; Andersen, Z.J.; Beelen, R.; Samoli, E.; Stafoggia, M.; Weinmayr, G.; Hoffmann, B.; Fischer, P.; Nieuwenhuijsen, M.J.; Brunekreef, B.; et al. Air pollution and lung cancer incidence in 17 European cohorts: Prospective analyses from the European Study of Cohorts for Air Pollution Effects (ESCAPE). Lancet Oncol. 2013, 14, 813–822. [Google Scholar] [CrossRef]
- Belis, C.A.; Karagulian, F.; Larsen, B.R.; Hopke, P.K. Critical review and meta-analysis of ambient particulate matter source apportionment using receptor models in Europe. Atmos. Environ. 2013, 69, 94–108. [Google Scholar] [CrossRef]
- Morawska, L.; Thomas, S.; Gilbert, D.; Greenaway, C.; Rijnders, E. A study of the horizontal and vertical profile of submicrometer particles in relation to a busy road. Atmos. Environ. 1999, 33, 1261–1274. [Google Scholar] [CrossRef]
- Kassomenos, P.A.; Kelessis, A.; Paschalidou, A.K.; Petrakakis, M. Identification of sources and processes affecting particulate pollution in Thessaloniki, Greece. Atmos. Environ. 2011, 45, 7293–7300. [Google Scholar] [CrossRef]
- Karagulian, F.; Belis, C.A.; Dora, C.F.C.; Prüss-Ustün, A.M.; Bonjour, S.; Adair-Rohani, H.; Amann, M. Contributions to cities’ ambient particulate matter (PM): A systematic review of local source contributions at global level. Atmos. Environ. 2015, 120, 475–483. [Google Scholar] [CrossRef]
- Weber, S. Spatio-temporal covariation of urban particle number concentration and ambient noise. Atmos. Environ. 2009, 43, 5518–5525. [Google Scholar] [CrossRef]
- Wurzler, S.; Hebbinghaus, H.; Steckelbach, I.; Schulz, T.; Pompetzki, W.; Memmesheimer, M.; Jakobs, H.; Schöllnhammer, T.; Nowag, S.; Diegmann, V. Regional and local effects of electric vehicles on air quality and noise. Meteorol. Z. 2016, 25, 319–325. [Google Scholar]
- Dekoninck, L.; Botteldooren, D.; Decoensel, B.; Int Panis, L. Spectral noise measurements supply instantaneous traffic information for multidisciplinary mobility and traffic related projects. In Proceedings of the 45th International Congress and Exposition on Noise Control Engineering (Internoise 2016): Towards a Quieter Future, Hamburg, Germany, 21–24 August 2016. [Google Scholar]
- Fernández-Camacho, R.; Brito Cabeza, I.; Aroba, J.; Gómez-Bravo, F.; Rodríguez, S.; de la Rosa, J. Assessment of ultrafine particles and noise measurements using fuzzy logic and data mining techniques. Sci. Total Environ. 2015, 512–513, 103–113. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.W.; Davies, H.; Cohen, M.A.; Mallach, G.; Kaufman, J.D.; Adar, S.D. The spatial relationship between traffic-generated air pollution and noise in 2 US cities. Environ. Res. 2009, 109, 334–342. [Google Scholar] [CrossRef] [PubMed]
- Boogaard, H.; Borgman, F.; Kamminga, J.; Hoek, G. Exposure to ultrafine and fine particles and noise during cycling and driving in 11 Dutch cities. Atmos. Environ. 2009, 43, 4234–4242. [Google Scholar] [CrossRef]
- Can, A.; Rademaker, M.; van Renterghem, T.; Mishra, V.; van Poppel, M.; Touhafi, A.; Theunis, J.; de Baets, B.; Botteldooren, D. Correlation analysis of noise and ultrafine particle counts in a street canyon. Sci. Total Environ. 2011, 409, 564–572. [Google Scholar] [CrossRef] [PubMed]
- Shu, S.; Yang, P.; Zhu, Y. Correlation of noise levels and particulate matter concentrations near two major freeways in Los Angeles, California. Environ. Pollut. 2014, 193, 130–137. [Google Scholar] [CrossRef] [PubMed]
- Weber, S.; Litschke, T. Variation of particle concentrations and environmental noise on the urban neighbourhood scale. Atmos. Environ. 2008, 42, 7179–7183. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO Acoustics—Normal Equal-Loudness-Level Contours; International Organization for Standardization, Technical Committee ISO/TC 43, Acoustics; International Organization for Standardization: Geneva, Switzerland, 2003; p. 15. [Google Scholar]
- Borrego, C.; Costa, A.M.; Ginja, J.; Amorim, M.; Coutinho, M.; Karatzas, K.; Sioumis, T.; Katsifarakis, N.; Konstantinidis, K.; de Vito, S.; et al. Assessment of air quality microsensors versus reference methods: The EuNetAir joint exercise. Atmos. Environ. 2016, 147, 246–263. [Google Scholar] [CrossRef]
- Daly, A.; Zannetti, P. Air Pollution Modeling–An Overview. In Chapter 2 of AMBIENT AIR POLLUTION; Zannetti, P., Al-Ajmi, D., Al-Rashied, S., Eds.; The Arab School for Science and Technology (ASST); The EnviroComp Institute: Fremont, CA, USA, 2007. [Google Scholar]
- Lateb, M.; Meroney, R.N.; Yataghene, M.; Fellouah, H.; Saleh, F.; Boufadel, M.C. On the use of numerical modelling for near-field pollutant dispersion in urban environments—A review. Environ. Pollut. 2016, 208, 271–283. [Google Scholar] [CrossRef] [PubMed]
- Paas, B.; Schneider, C. A comparison of model performance between ENVI-met and Austal2000 for particulate matter. Atmos. Environ. 2016, 145, 392–404. [Google Scholar] [CrossRef]
- Vlachogianni, A.; Kassomenos, P.; Karppinen, A.; Karakitsios, S.; Kukkonen, J. Evaluation of a multiple regression model for the forecasting of the concentrations of NOx and PM10 in Athens and Helsinki. Sci. Total Environ. 2011, 409, 1559–1571. [Google Scholar] [CrossRef] [PubMed]
- Santos, G.; Fernández-Olmo, I. A proposed methodology for the assessment of arsenic, nickel, cadmium and lead levels in ambient air. Sci. Total Environ. 2016, 554–555, 155–166. [Google Scholar] [CrossRef] [PubMed]
- Merbitz, H.; Buttstädt, M.; Michael, S.; Dott, W.; Schneider, C. GIS-based identification of spatial variables enhancing heat and poor air quality in urban areas. Appl. Geogr. 2012, 33, 94–106. [Google Scholar] [CrossRef]
- Merbitz, H.; Fritz, S.; Schneider, C. Mobile measurements and regression modeling of the spatial particulate matter variability in an urban area. Sci. Total Environ. 2012, 438, 389–403. [Google Scholar] [CrossRef] [PubMed]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Kukkonen, J. Extensive evaluation of neural network models for the prediction of NO2 and PM10 concentrations, compared with a deterministic modelling system and measurements in central Helsinki. Atmos. Environ. 2003, 37, 4539–4550. [Google Scholar] [CrossRef]
- Wu, W.; Dandy, G.C.; Maier, H.R. Protocol for developing ANN models and its application to the assessment of the quality of the ANN model development process in drinking water quality modelling. Environ. Model. Softw. 2014, 54, 108–127. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Neural network modelling and prediction of hourly NOx and NO2 concentrations in urban air in London. Atmos. Environ. 1999, 33, 709–719. [Google Scholar] [CrossRef]
- Hooyberghs, J.; Mensink, C.; Dumont, G.; Fierens, F.; Brasseur, O. A neural network forecast for daily average PM concentrations in Belgium. Atmos. Environ. 2005, 39, 3279–3289. [Google Scholar] [CrossRef]
- Cai, M.; Yin, Y.; Xie, M. Prediction of hourly air pollutant concentrations near urban arterials using artificial neural network approach. Transp. Res. Part Transp. Environ. 2009, 14, 32–41. [Google Scholar] [CrossRef]
- Kraftfahrtbundesamt Zentrales Fahrzeugregister. Available online: http://www.kba.de/cln_031/nn_191172/DE/Statistik/Fahrzeuge/Bestand/FahrzeugklassenAufbauarten/b__fzkl__zeitreihe.html (accessed on 15 October 2016).
- Hájek, P.; Olej, V. Ozone prediction on the basis of neural networks, support vector regression and methods with uncertainty. Ecol. Inform. 2012, 12, 31–42. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Günther, F.; Fritsch, S. neuralnet: Training of Neural Networks. R J. 2016, 2, 30–38. [Google Scholar]
- Razavi, S.; Tolson, B.A. A New Formulation for Feedforward Neural Networks. IEEE Trans. Neural Netw. 2011, 22, 1588–1598. [Google Scholar] [CrossRef] [PubMed]
- Stamenković, L.J.; Antanasijević, D.Z.; Ristić, M.Đ.; Perić-Grujić, A.A.; Pocajt, V.V. Modeling of ammonia emission in the USA and EU countries using an artificial neural network approach. Environ. Sci. Pollut. Res. 2015, 22, 18849–18858. [Google Scholar] [CrossRef] [PubMed]
- May, R.J.; Maier, H.R.; Dandy, G.C.; Fernando, T.M.K.G. Non-linear variable selection for artificial neural networks using partial mutual information. Environ. Model. Softw. 2008, 23, 1312–1326. [Google Scholar] [CrossRef]
- Manousakas, M.; Papaefthymiou, H.; Diapouli, E.; Migliori, A.; Karydas, A.G.; Bogdanovic-Radovic, I.; Eleftheriadis, K. Assessment of PM2.5 sources and their corresponding level of uncertainty in a coastal urban area using EPA PMF 5.0 enhanced diagnostics. Sci. Total Environ. 2017, 574, 155–164. [Google Scholar] [CrossRef] [PubMed]
- Morelli, X.; Foraster, M.; Aguilera, I.; Basagana, X.; Corradi, E.; Deltell, A.; Ducret-Stich, R.; Phuleria, H.; Ragettli, M.S.; Rivera, M.; et al. Short-term associations between traffic-related noise, particle number and traffic flow in three European cities. Atmos. Environ. 2015, 103, 25–33. [Google Scholar] [CrossRef]
- Merbitz, H. Feinstaubkonzentration in Abhängigkeit von Witterung und Großwetterlagen im Raum Aachen. Aachen. Geogr. Arb. 2009, 46, 121–134. [Google Scholar]
- Merbitz, H.; Ketzler, G.; Schneider, C. Untersuchungen zu den Windverhältnissen im Innenstadtbereich von Aachen. Aachen. Geogr. Arb. 2010, Heft 46, 97–116. [Google Scholar]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 2nd ed.; John Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Sandberg, U.; Ejsmont, J.A. Tyre/Road Noise Reference Book; INFORMEX: Kisa, Sweden; Harg, Sweden, 2002. [Google Scholar]
- Bowden, G.J.; Dandy, G.C.; Maier, H.R. Input determination for neural network models in water resources applications. Part 1—background and methodology. J. Hydrol. 2005, 301, 75–92. [Google Scholar] [CrossRef]
- Fernando, T.M.K.G.; Maier, H.R.; Dandy, G.C. Selection of input variables for data driven models: An average shifted histogram partial mutual information estimator approach. J. Hydrol. 2009, 367, 165–176. [Google Scholar] [CrossRef]
- May, R.J.; Maier, H.R.; Dandy, G.C. Data splitting for artificial neural networks using SOM-based stratified sampling. Neural Netw. 2010, 23, 283–294. [Google Scholar] [CrossRef] [PubMed]
- Johnson, S.R.; Jurs, P.C. Prediction of the Clearing Temperatures of a Series of Liquid Crystals from Molecular Structure. Chem. Mater. 1999, 11, 1007–1023. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Clarendon Press: Oxford, UK; Oxford University Press: Oxford, UK; New York, NY, USA, 1995. [Google Scholar]
- Grimm, H.; Eatough, D.J. Aerosol Measurement: The Use of Optical Light Scattering for the Determination of Particulate Size Distribution, and Particulate Mass, Including the Semi-Volatile Fraction. J. Air Waste Manag. Assoc. 2009, 59, 101–107. [Google Scholar] [CrossRef] [PubMed]
- LANUV Umgebungslärm in NRW. Available online: http://www.umgebungslaerm-kartierung.nrw.de/ (accessed on 5 December 2016).
- Schneider, C.; Ketzler, G. Klimamessstation Aachen-Hörn—Monatsberichte Februar, Mai, September/2014; Lehr- und Forschungsgebiet Physische Geographie und Klimatologie, Geographisches Institut, RWTH Aachen: Aachen, Germany, 2016. [Google Scholar]
- Sousa, S.; Martins, F.; Alvimferraz, M.; Pereira, M. Multiple linear regression and artificial neural networks based on principal components to predict ozone concentrations. Environ. Model. Softw. 2007, 22, 97–103. [Google Scholar] [CrossRef]
- Pederzoli, A.; Thunis, P.; Georgieva, E.; Borge, R.; Carruthers, D. Performance criteria for the benchmarking of air quality model regulatory applications: The “target” aproach. In Proceedings of the 14th Conference on Harmonisation within Atmospheric Dispersion Modelling for Regulatory Purposes Kos, Greece, 2–6 October 2011; pp. 297–301. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Thunis, P.; Georgieva, E.; Pederzoli, A. A tool to evaluate air quality model performances in regulatory applications. Environ. Model. Softw. 2012, 38, 220–230. [Google Scholar] [CrossRef]
- Cox, W.M.; Tikvart, J.A. A statistical procedure for determining the best performing air quality simulation model. Atmos. Environ. Part Gen. Top. 1990, 24, 2387–2395. [Google Scholar] [CrossRef]
- Yassin, M.F. Numerical modeling on air quality in an urban environment with changes of the aspect ratio and wind direction. Environ. Sci. Pollut. Res. 2013, 20, 3975–3988. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.C.; Hanna, S.R. Air quality model performance evaluation. Meteorol. Atmos. Phys. 2004, 87, 167–196. [Google Scholar] [CrossRef]
- Stow, C.A.; Jolliff, J.; McGillicuddy, D.J.; Doney, S.C.; Allen, J.I.; Friedrichs, M.A.M.; Rose, K.A.; Wallhead, P. Skill assessment for coupled biological/physical models of marine systems. J. Mar. Syst. 2009, 76, 4–15. [Google Scholar] [CrossRef]
- Ketzel, M.; Omstedt, G.; Johansson, C.; Düring, I.; Pohjola, M.; Oettl, D.; Gidhagen, L.; Wåhlin, P.; Lohmeyer, A.; Haakana, M.; et al. Estimation and validation of PM2.5/PM10 exhaust and non-exhaust emission factors for practical street pollution modelling. Atmos. Environ. 2007, 41, 9370–9385. [Google Scholar] [CrossRef]
- Amato, F.; Cassee, F.R.; Denier van der Gon, H.A.C.; Gehrig, R.; Gustafsson, M.; Hafner, W.; Harrison, R.M.; Jozwicka, M.; Kelly, F.J.; Moreno, T.; et al. Urban air quality: The challenge of traffic non-exhaust emissions. J. Hazard. Mater. 2014, 275, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Gidhagen, L.; Johansson, C.; Langner, J.; Olivares, G. Simulation of NOx and ultrafine particles in a street canyon in Stockholm, Sweden. Atmos. Environ. 2004, 38, 2029–2044. [Google Scholar] [CrossRef]
- Ketzel, M.; Berkowicz, R. Multi-plume aerosol dynamics and transport model for urban scale particle pollution. Atmos. Environ. 2005, 39, 3407–3420. [Google Scholar] [CrossRef]
- Zhu, Y.; Kuhn, T.; Mayo, P.; Hinds, W.C. Comparison of Daytime and Nighttime Concentration Profiles and Size Distributions of Ultrafine Particles near a Major Highway. Environ. Sci. Technol. 2006, 40, 2531–2536. [Google Scholar] [CrossRef] [PubMed]
- Paas, B.; Schmidt, T.; Markova, S.; Maras, I.; Ziefle, M.; Schneider, C. Small-scale variability of particulate matter and perception of air quality in an inner-city recreational area in Aachen, Germany. Meteorol. Z. 2016, 25, 305–317. [Google Scholar]
- Soret, A.; Guevara, M.; Baldasano, J.M. The potential impacts of electric vehicles on air quality in the urban areas of Barcelona and Madrid (Spain). Atmos. Environ. 2014, 99, 51–63. [Google Scholar] [CrossRef]








| Parameter | Ordering | Tuning |
|---|---|---|
| Initial learning rate | 0.9 | 0.1 |
| Initial neighborhood size | 3.6 (2.7) | 1 |
| Epochs | 2 | 20 |
| ILn | 5 (4) | 6 (5) | 6 (5) | 7 (6) |
| IVC [AIC] | PM10 (bc) | PM10 (bc) | PM10 (bc) | PM10 (bc) |
| Ta [−428] | RH [−242] | RH [−171] | RH [−241] | |
| P [−843] | Ta [−274] | Ta [−235] | Ta [−283] | |
| Ig [−868] | Ig [−358] | WS [−251] | Ig [−365] | |
| WS [−866] | P [−366] | P [−270 ] | WS [−423] | |
| WD [−832] | WS [−346] | WD [−246] | P [−430] | |
| RH [−810] | WD[−388] | Ig [−210] | WD [−421] | |
| SPLeq [−6] | SPLeq [−8] | SPLeq [−10] | SPLeq [−9] | |
| SPLeq15Hz(A) [−1] | SPLeq15Hz [−2] | SPLeq15Hz [−1] | SPLeq15Hz(A) [−4] | |
| SPLeq16kHz [23] | SPLeq34Hz [10] | SPLeq15Hz(A) [2] | SPLeq15Hz(A) [5] | |
| SPLeq63Hz(A) [51] | SPLeq34Hz(A) [14] | SPLeq63Hz(A) [27] | SPLeq34Hz [8] | |
| SPLeq15Hz [55] | SPLeq15Hz(A) [18] | SPLeq125Hz(A) [55] | SPLeq34Hz(A) [10] | |
| SPLeq34Hz(A) [70] | SPLeq16kHz [45] | SPLeq34Hz [70] | SPLeq250Hz(A) [14] | |
| SPLeq16kHz(A) [78] | SPLeq250Hz(A) [61] | SPLeq16kHz(A) [127] | SPLeq250Hz [19] | |
| SPLeq125Hz(A) [112] | SPLeq250Hz [66] | SPLeq8kHz [154] | SPLeq16kHz(A) [57] | |
| SPLeq8kHz [137] | SPLeq16kHz(A) [83] | SPLeq250Hz(A) [168] | SPLeq16kHz [73] | |
| SPLeq250Hz(A) [154] | SPLeq63Hz(A) [117] | SPLeq34Hz(A) [176] | SPLeq63Hz(A) [105] | |
| SPLeq63Hz [165] | SPLeq125Hz(A) [147] | SPLeq16kHz [189] | SPLeq125Hz(A) [133] | |
| SPLeq34Hz [174] | SPLeq8kHz [171] | SPLeq63Hz [201] | SPLeq63Hz [146] | |
| SPLeq125Hz [189] | SPLeq63Hz [183] | SPLeq8kHz(A) [207] | SPLeq125Hz [161] | |
| SPLeq250Hz [194] | SPLeq125Hz [199] | SPLeq125Hz [225] | SPLeq8kHz [184] | |
| SPLeq8kHz(A) [200] | SPLeq8kHz(A) [205] | SPLeq250Hz [229] | SPLeq8kHz(A) [189] | |
| SPLeq500Hz(A) [207] | SPLeq500Hz [212] | SPLeq4kHz(A) [241] | SPLeq500Hz [195] | |
| SPLeq4kHz [219] | SPLeq4kHz(A) [224] | SPLeq500Hz [247] | SPLeq4kHz [208] | |
| SPLeq1kHz [221] | SPLeq1kHz [225] | SPLeq500Hz(A) [250] | SPLeq1kHz [210] | |
| SPLeq4kHz(A) [226] | SPLeq4kHz [230] | SPLeq4kHz [253] | SPLeq4kHz(A) [215] | |
| SPLeq500Hz [230] | SPLeq500Hz(A) [233] | SPLeq2kHz(A) [257] | SPLeq500Hz(A) [218] | |
| SPLeq(A) [240] | SPLeq(A) [243] | SPLeq(A) [260] | SPLeq(A) [233] | |
| HLn | 6 (7) | 4 (3) | 5 (4) | 5 (4) |
| Transfer function | Hyp-Tan | Hyp-Tan | Log-Sig | Hyp-Tan |
| (Hyp-Tan) | (Hyp-Tan) | (Log-Sig) | (Hyp-Tan) | |
| OL | PM(0.25–1) | PM(0.25–2.5) | PM(0.25–10) | PNC(0.25–2.5) |
| Variable | PM(0.25–1) | PM(0.25–2.5) | PM(0.25–10) | PNC(0.25–2.5) | SPL | ||
|---|---|---|---|---|---|---|---|
| (μg·m−3) | (#·dm−3) | (dB) | |||||
| “Aachen-Karlsgraben” | AM: 15.9 SD: 4.2 | AM: 19.4 SD: 5.3 | AM: 30.4 SD: 8.9 | AM: 545 SD: 217 | Leq: 74.1 L10: 79.7 L90: 63.4 | ||
| “Münster-Aasee” | AM: 16.3 SD: 10.2 | AM: 18.4 SD: 9.9 | AM: 28.7 SD: 9.1 | AM: 545 SD: 460 | Leq: 69.5 L10: 75.2 L90: 62.0 | ||
| OL | “Aachen-Karlsgraben” | “Münster-Aasee” | ||||||
|---|---|---|---|---|---|---|---|---|
| PM(0.25–1) | PM(0.25–2.5) | PM(0.25–10) | PNC(0.25–2.5) | PM(0.25–1) | PM(0.25–2.5) | PM(0.25–10) | PNC(0.25–2.5) | |
| RMSE | 5.97 (4.27) [μg·m−3] | 6.88 (5.09) [μg·m−3] | 7.78 (9.35) [μg·m−3] | 167 (208) [#·dm−3] | 12.29 (10.11) [μg·m−3] | 5.71 (5.66) [μg·m−3] | 6.50 (8.92) [μg·m−3] | 205 (259) [#·dm−3] |
| FB | −0.17 (0.14) | −0.22 (−0.09) | −0.02 (−0.04) | −0.02 (−0.01) | 0.30 (0.16) | −0.04 (0.00) | 0.06 (0.06) | 0.13 (0.37) |
| MEF | −1.15 (−0.27) | −0.89 (−0.41) | 0.31 (0.05) | 0.25 (0.26) | −0.01 (0.11) | 0.82 (0.67) | 0.64 (0.13) | 0.85 (0.78) |
| R2 | 0.05 (0.16) | 0.13 (0.35) | 0.48 (0.14) | 0.28 (0.26) | 0.70 (0.11) | 0.85 (0.65) | 0.78 (0.69) | 0.89 (0.90) |
| slope | 0.24 (0.01) | 0.02 (0.81) | 0.18 (0.02) | 0.11 (0.17) | 0.03 (0.11) | 1.02 (0.62) | 0.43 (0.03) | 1.04 (0.93) |
| SD’ | 4.34 (0.02) [μg·m−3] | 0.32 (5.93) [μg·m−3] | 2.43 (0.62) [μg·m−3] | 41 (82) [#·dm−3] | 0.54 (1.06) [μg·m−3] | 14.84 (7.66) [μg·m−3] | 5.21 (0.36) [μg·m−3] | 591 (539) [#·dm−3] |
| SD | 4.07 (3.78) [μg·m−3] | 5.01 (4.29) [μg·m−3] | 9.39 (9.62) [μg·m−3] | 194 (241) [#·dm−3] | 12.24 (10.78) [μg·m−3] | 13.39 (9.91) [μg·m−3] | 10.79 (9.57) [μg·m−3] | 538 (554) [#·dm−3] |
| 16.3 (15.6) [μg·m−3] | 20.0 (19.2) [μg·m−3] | 30.0 (31.8) [μg·m−3] | 518 (542) [#·dm−3] | 18.6 (15.5) [μg·m−3] | 21.7 (17.3) [μg·m−3] | 27.3 (27.7) [μg·m−3] | 652 (662) [#·dm−3] | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paas, B.; Stienen, J.; Vorländer, M.; Schneider, C. Modelling of Urban Near-Road Atmospheric PM Concentrations Using an Artificial Neural Network Approach with Acoustic Data Input. Environments 2017, 4, 26. https://doi.org/10.3390/environments4020026
Paas B, Stienen J, Vorländer M, Schneider C. Modelling of Urban Near-Road Atmospheric PM Concentrations Using an Artificial Neural Network Approach with Acoustic Data Input. Environments. 2017; 4(2):26. https://doi.org/10.3390/environments4020026
Chicago/Turabian StylePaas, Bastian, Jonas Stienen, Michael Vorländer, and Christoph Schneider. 2017. "Modelling of Urban Near-Road Atmospheric PM Concentrations Using an Artificial Neural Network Approach with Acoustic Data Input" Environments 4, no. 2: 26. https://doi.org/10.3390/environments4020026
APA StylePaas, B., Stienen, J., Vorländer, M., & Schneider, C. (2017). Modelling of Urban Near-Road Atmospheric PM Concentrations Using an Artificial Neural Network Approach with Acoustic Data Input. Environments, 4(2), 26. https://doi.org/10.3390/environments4020026