Susceptibility to Seismic Amplification and Earthquake Probability Estimation Using Recurrent Neural Network (RNN) Model in Odisha, India
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Geological Settings
2.3. Data
2.4. Thematic Layer Preparation
Importance of Factors
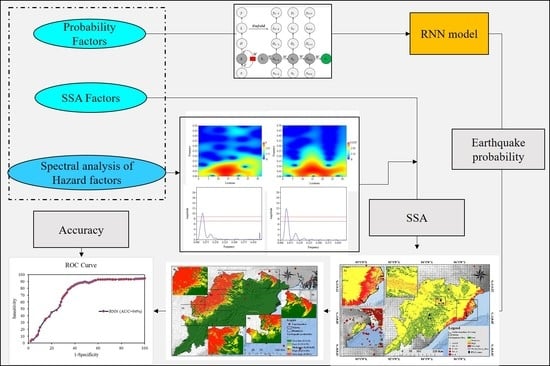
2.5. Methodology
2.5.1. Spectral Analysis
2.5.2. Short-Time Fourier Transform
2.5.3. Estimation of Distance from Source-to-Site, PGA and Intensity
2.5.4. Recurrent Neural Network
2.5.5. Data Presentation for RNN
2.5.6. Model Evaluation Methods
3. Results
3.1. Periodogram Plotting of PGA and Intensity
3.2. Short-Time Fourier Transform
3.3. Susceptibility to Seismic Amplification (SSA)
3.4. Earthquake Probability Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gupta, S.; Mohanty, W.K.; Mandal, A.; Misra, S. Ancient terrane boundaries as probable seismic hazards: A case study from the northern boundary of the Eastern Ghats Belt, India. Geosci. Front. 2014, 5, 17–24. [Google Scholar] [CrossRef] [Green Version]
- Kumar, T.S.; Mahendra, R.; Nayak, S.; Radhakrishnan, K.; Sahu, K. Coastal Vulnerability Assessment for Orissa State, East Coast of India. J. Coast. Res. 2010, 263, 523–534. [Google Scholar] [CrossRef]
- Mahala, S.C. Geology, Chemistry and Genesis of Thermal Springs of Odisha, India. Springer Briefs Earth Sci. 2019, 5, 1572–1577. [Google Scholar] [CrossRef]
- Rajendran, C.P.; Rajendran, K.; John, B. The 1993 Killari (Latur), central India, earthquake: An example of fault reactivation in the Precambrian crust. Geol. 1996, 24, 651. [Google Scholar] [CrossRef]
- Di Giulio, G.; The L’Aquila Experiment Team; Marzorati, S.; Bergamaschi, F.; Bordoni, P.; Cara, F.; D’Alema, E.; Ladina, C.; Massa, M. Local variability of the ground shaking during the 2009 L’Aquila earthquake (April 6, 2009—Mw 6.3): The case study of Onna and Monticchio villages. Bull. Earthq. Eng. 2011, 9, 783–807. [Google Scholar] [CrossRef]
- Jena, R.; Pradhan, B.; Beydoun, G.; Nizamuddin; Ardiansyah; Sofyan, H.; Affan, M. Integrated model for earthquake risk assessment using neural network and analytic hierarchy process: Aceh province, Indonesia. Geosci. Front. 2020, 11, 613–634. [Google Scholar] [CrossRef]
- Ehret, D.; Hannich, D. Seismic Microzonation based on geotechnical Parameters-Estimation of Site Effects in Bucharest (Romania). AGUFM 2004, 2004, S43A-0972. [Google Scholar]
- Theilen-Willige, B. Detection of local site conditions influencing earthquake shaking and secondary effects in Southwest-Haiti using remote sensing and GIS-methods. Nat. Hazards Earth Syst. Sci. 2010, 10, 1183–1196. [Google Scholar] [CrossRef]
- Levchenko, O.V. Tectonic aspects of intraplate seismicity in the northeastern Indian Ocean. Tectonophys. 1989, 170, 125–139. [Google Scholar] [CrossRef]
- Rai, A.; Tripathy, S.; Sahu, S. The May 21 st, 2014 Bay of Bengal earthquake: Implications for intraplate stress regime. Curr. Sci. (00113891) 2015, 108. [Google Scholar]
- Bhatia, S.C.; Kumar, M.R.; Gupta, H.K. A probabilistic seismic hazard map of India and adjoining regions. Ann. Geophys. 1999, 42. [Google Scholar] [CrossRef]
- Parvez, I.; Vaccari, F.; Panza, G.F. A deterministic seismic hazard map of India and adjacent areas. Geophys. J. Int. 2003, 155, 489–508. [Google Scholar] [CrossRef]
- Jaiswal, K.; Sinha, R. Probabilistic Seismic-Hazard Estimation for Peninsular India. Bull. Seism. Soc. Am. 2007, 97, 318–330. [Google Scholar] [CrossRef] [Green Version]
- Raghukanth, S.T.G.; Iyengar, R.N. Seismic hazard estimation for Mumbai city. Curr. Sci. 2006, 91, 1486–1494. [Google Scholar]
- Anbazhagan, P.; Vinod, J.S.; Sitharam, T. Probabilistic seismic hazard analysis for Bangalore. Nat. Hazards 2008, 48, 145–166. [Google Scholar] [CrossRef]
- Cornell, C.A. Engineering seismic risk analysis. Bull. Seism. Soc. Am. 1968, 58, 1583–1606. [Google Scholar]
- Atkinson, G.M.; Boore, D.M. Earthquake Ground-Motion Prediction Equations for Eastern North America. Bull. Seism. Soc. Am. 2006, 96, 2181–2205. [Google Scholar] [CrossRef]
- Petersen, M.D.; Mueller, C.S.; Moschetti, M.P.; Hoover, S.M.; Llenos, A.L.; Ellsworth, W.L.; Michael, A.J.; Rubinstein, J.L.; McGarr, A.F.; Rukstales, K.S. Seismic-Hazard Forecast for 2016 Including Induced and Natural Earthquakes in the Central and Eastern United States. Seism. Res. Lett. 2016, 87, 1327–1341. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Brant, L.; Wu, Y.-M.; Taheri, H. Probability-based PGA estimations using the double-lognormal distribution: Including site-specific seismic hazard analysis for four sites in Taiwan. Soil Dyn. Earthq. Eng. 2012, 42, 177–183. [Google Scholar] [CrossRef]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives: Preferences and Value Trade-Offs; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Mohanty, W.K.; Walling, M.Y.; Vaccari, F.; Tripathy, T.; Panza, G.F. Modeling of SH- and P-SV-wave fields and seismic microzonation based on response spectra for Talchir Basin, India. Eng. Geol. 2009, 104, 80–97. [Google Scholar] [CrossRef]
- Sarkar, S.; Saha, A. Structure and Tectonics of the Singhbhum-Orissa Iron Ore Craton, Eastern India. In Structure and Tectonics of Precambrian Rocks of India; 1983; pp. 1–25. Available online: http://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=9063125 (accessed on 20 February 2020).
- India, G.S.o.; Dasgupta, S.; Narula, P.; Acharyya, S.; Banerjee, J. Seismotectonic atlas of India and Its Environs; Special Publication Series 59; Geological Survey of India: Calcutta, India, 2000. [Google Scholar]
- Mahalik, N. Geology of the contact between the Eastern Ghats Belt and North Orissa Carton, India. J. Geol. Soc. India 1994, 44, 41–51. Available online: https://ci.nii.ac.jp/naid/10007644438/ (accessed on 25 February 2020).
- Gupta, S. Strain localization, granulite formation and geodynamic setting of ‘hot orogens’: A case study from the Eastern Ghats Province, India. Geol. J. 2011, 47, 334–351. [Google Scholar] [CrossRef]
- Mukhopadhayay, A.; Chaudhuri, P.; Banerji, A. Contemporaneous intrabasinal faulting in Gondwana basin—The Jurabaga fault of Ib River Coalfield, a type example. J. Geol. Soc. India 1984, 25, 557–563. [Google Scholar]
- Kolathayar, S.; Sitharam, T.G.; Vipin, K.S. Deterministic seismic hazard macrozonation of India. J. Earth Syst. Sci. 2012, 121, 1351–1364. [Google Scholar] [CrossRef] [Green Version]
- Iyengar, R.N.; Kanth, S.T.G.R. Attenuation of Strong Ground Motion in Peninsular India. Seism. Res. Lett. 2004, 75, 530–540. [Google Scholar] [CrossRef]
- Jena, R.; Pradhan, B. Integrated ANN-cross-validation and AHP-TOPSIS model to improve earthquake risk assessment. Int. J. Disaster Risk Reduct. 2020, 101723. [Google Scholar] [CrossRef]
- Alizadeh, M.; Ngah, I.; Hashim, M.; Pradhan, B.; Pour, A.B. A Hybrid Analytic Network Process and Artificial Neural Network (ANP-ANN) Model for Urban Earthquake Vulnerability Assessment. Remote. Sens. 2018, 10, 975. [Google Scholar] [CrossRef] [Green Version]
- Bathrellos, G.; Skilodimou, D.; Chousianitis, K.; Youssef, A.; Pradhan, B. Suitability estimation for urban development using multi-hazard assessment map. Sci. Total. Environ. 2017, 575, 119–134. [Google Scholar] [CrossRef]
- Soe, M.; Ryutaro, T.; Ishiyama, D.; Takashima, I.; Charusiri, K.W.-I.a.P. Remote sensing and GIS based approach for earthquake probability map: A case study of the northern Sagaing fault area, Myanmar. J. Geol. Soc. Thailand 2009, 1, 29–46. [Google Scholar]
- Burtin, A.; Bollinger, L.; Vergne, J.; Cattin, R.; Nábělek, J.L. Spectral analysis of seismic noise induced by rivers: A new tool to monitor spatiotemporal changes in stream hydrodynamics. J. Geophys. Res. Space Phys. 2008, 113, 5. [Google Scholar] [CrossRef] [Green Version]
- Visalakshmi, G.; Praveen, I.; Ramesh, K.; Rao, S.K.; Bharathi, V.L. Power spectrum Estimation of Seismic Wave using Periodogram method. Int. J. Pure Appl. Math. 2017, 114, 191–199. [Google Scholar]
- Schuster, A.; Hemsalech, G. VI. On the constitution of the electric spark. Philos. Trans. R. Soc. London. Ser. A Contain. Pap. a Math. or Phys. Character (1896-1934) 1900, 193, 189–213. [Google Scholar] [CrossRef]
- Lu, W.; Li, F. Seismic spectral decomposition using deconvolutive short-time Fourier transform spectrogram. Geophysics. 2013, 78, V43–V51. [Google Scholar] [CrossRef]
- Joyner, W.; Boore, D.M.; Porcella, R. Peak horizontal acceleration and velocity from strong motion records including records from the 1979 Imperial Valley, California, earthquake. Open-File Report 1981, 71, 2011–2038. [Google Scholar] [CrossRef]
- Boore, D.M.; Joyner, W.B. The empirical prediction of ground motion. Bull. Seism. Soc. Am. 1982, 72, S43–S60. [Google Scholar]
- Campbell, G.S. Soil Physics with BASIC: Transport Models for Soil-Plant Systems, 1st ed.; Elsevier: Oxford, UK, 1985; Volume 14. [Google Scholar]
- Fukushima, Y.; Tanaka, T. A new attenuation relation for peak horizontal acceleration of strong earthquake ground motion in Japan. Bull. Seism. Soc. Am. 1990, 80, 757–783. [Google Scholar]
- Xu, S.; Niu, R. Displacement prediction of Baijiabao landslide based on empirical mode decomposition and long short-term memory neural network in Three Gorges area, China. Comput. Geosci. 2018, 111, 87–96. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Wang, M.; Peng, L.; Hong, H. Comparative study of landslide susceptibility mapping with different recurrent neural networks. Comput. Geosci. 2020, 138, 104445. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I.; Hong, H.; Chen, W.; Xu, C. Applying Information Theory and GIS-based quantitative methods to produce landslide susceptibility maps in Nancheng County, China. Landslides 2016, 14, 1091–1111. [Google Scholar] [CrossRef]
- Ercanoglu, C.G.M.; Ercanoglu, M.; Gokceoglu, C. Assessment of landslide susceptibility for a landslide-prone area (north of Yenice, NW Turkey) by fuzzy approach. Environ. Earth Sci. 2002, 41, 720–730. [Google Scholar] [CrossRef]
- Matthews, B. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. et Biophys. Acta (BBA) Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. J. Mach. Learn. Technol. 2011, 2. [Google Scholar] [CrossRef]
- Dhar, S.; Rai, A.K.; Nayak, P. Estimation of seismic hazard in Odisha by remote sensing and GIS techniques. Nat. Hazards 2016, 86, 695–709. [Google Scholar] [CrossRef]
- Mohanty, W.K.; Walling, M.Y.; Nath, S.K.; Pal, I. First Order Seismic Microzonation of Delhi, India Using Geographic Information System (GIS). Nat. Hazards 2006, 40, 245–260. [Google Scholar] [CrossRef]
- Sitharam, T.; Anbazhagan, P. Seismic microzonation: Principles, practices and experiments. EJGE Special Volume Bouquet 2008, 8. Available online: http://www.ejge.com/Bouquet08/Sitharam/Sitharam_abs.pdf (accessed on 28 March 2020).
- Grelle, G.; Bonito, L.; Lampasi, A.; Revellino, P.; Guerriero, L.; Sappa, G.; Guadagno, F.M. SiSeRHMap v1.0: A simulator for mapped seismic response using a hybrid model. Geosci. Model Dev. 2016, 9, 1567–1596. [Google Scholar] [CrossRef] [Green Version]
- Aucelli, P.P.; Di Paola, G.; Valente, E.; Amato, V.; Bracone, V.; Cesarano, M.; Di Capua, G.; Scorpio, V.; Capalbo, A.; Pappone, G.; et al. First assessment of the local seismic amplification susceptibility of the Isernia Province (Molise Region, Southern Italy) by the integration of geological and geomorphological studies related to the first level seismic microzonation project. Environ. Earth Sci. 2018, 77, 118. [Google Scholar] [CrossRef]
- Rout, S.; Nanda, R. Deterministic Seismic Hazard Assessment at Bed Rock Level: Case Study for the City of Bhubaneswar, India. Int. J. Eng.Technol. 2015, 7, 599–610. [Google Scholar]
- Mandal, H.S.; Shukla, A.K.; Khan, P.K.; Mishra, O.P. A New Insight into Probabilistic Seismic Hazard Analysis for Central India. Pure Appl. Geophys. 2013, 170, 2139–2161. [Google Scholar] [CrossRef] [Green Version]
- United Nations Development Program, Enhancing Institutional and Community Resilience to Disasters and Climate Change. Hazard Risk and Vulnerability Analysis (HRVA) of the City of Bhubaneswar (Odisha). Final Report November 2014, 174p. Available online: https://www.ndmindia.nic.in/images/pdf/HazardRiskandVulnerabilityAnalysis(HRVA)oftheCityofBhubaneswar(Odisha).pdf (accessed on 28 April 2020).
- Fanos, A.M.; Pradhan, B. A Novel Hybrid Machine Learning-Based Model for Rockfall Source Identification in Presence of Other Landslide Types Using LiDAR and GIS. Earth Syst. Environ. 2019, 3, 491–506. [Google Scholar] [CrossRef]
- Fanos, A.M.; Pradhan, B. Laser Scanning Systems and Techniques in Rockfall Source Identification and Risk Assessment: A Critical Review. Earth Syst. Environ. 2018, 2, 163–182. [Google Scholar] [CrossRef]
- Jena, R.; Pradhan, B. A Model for Visual Assessment of Fault Plane Solutions and Active Tectonics Analysis Using the Global Centroid Moment Tensor Catalog. Earth Syst. Environ. 2019, 4, 197–211. [Google Scholar] [CrossRef]









| Assessment | Raw Data | Input Parameters | Methods | Resolution and Scale |
|---|---|---|---|---|
| Susceptibility to seismic amplification (SSA) | Digital elevation model (DEM) and geological information | Amplification factor elevation Slope curvature | Weighted overlay using predefined weights | 30 m and 1:30,000 |
| Earthquake probability assessment (EPA) | DEM, geological data, earthquake inventory, geo-structural information, attenuation relationship | Elevation slope Curvature magnitude density Depth density Epicenter density Proximity to epicenters Fault density Proximity to fault Geology | Recurrent neural network (RNN) |
| Optimized Parameter | Suitable Values for RNN | Description |
|---|---|---|
| Epoch | 100 | 100 times train the sample |
| Batch size | 64 | Size of each data batch |
| Drop out | 0 | Reduce overfitting |
| Optimizer | Adam | Adaptive moment estimation |
| Learning rate | Cross-entropy | Used for binary classification |
| Loss function | 0.001 | Weight updating speed |
| Predicted | |||
|---|---|---|---|
| Positive | Negative | ||
| Actual | Positive | 1750 | 50 |
| Negative | 100 | 800 | |
| Accuracy | 0.94 | ||
| Precision | 0.95 | ||
| Recall | 0.97 | ||
| F1 score | 0.96 | ||
| Threat score (TS) or critical success index (CSI) | 0.92 | ||
| Fowlkes–Mallows index (FM) | 0.95 | ||
| Class no. | Class | Area (km2) | Area (%) |
|---|---|---|---|
| 5 | Very-high | 48,900 | 31.4 |
| 4 | High | 3204 | 2.06 |
| 3 | Moderate | 3603 | 2.31 |
| 2 | Low | 493 | 0.32 |
| 1 | Very-low | 99,507 | 63.9 |
| Total | 155,707 | 100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jena, R.; Pradhan, B.; Alamri, A.M. Susceptibility to Seismic Amplification and Earthquake Probability Estimation Using Recurrent Neural Network (RNN) Model in Odisha, India. Appl. Sci. 2020, 10, 5355. https://doi.org/10.3390/app10155355
Jena R, Pradhan B, Alamri AM. Susceptibility to Seismic Amplification and Earthquake Probability Estimation Using Recurrent Neural Network (RNN) Model in Odisha, India. Applied Sciences. 2020; 10(15):5355. https://doi.org/10.3390/app10155355
Chicago/Turabian StyleJena, Ratiranjan, Biswajeet Pradhan, and Abdullah M. Alamri. 2020. "Susceptibility to Seismic Amplification and Earthquake Probability Estimation Using Recurrent Neural Network (RNN) Model in Odisha, India" Applied Sciences 10, no. 15: 5355. https://doi.org/10.3390/app10155355
APA StyleJena, R., Pradhan, B., & Alamri, A. M. (2020). Susceptibility to Seismic Amplification and Earthquake Probability Estimation Using Recurrent Neural Network (RNN) Model in Odisha, India. Applied Sciences, 10(15), 5355. https://doi.org/10.3390/app10155355