FEM Simulation of THz Detector Based on Sb and Bi88Sb12 Thermoelectric Thin Films
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Geometry and Mesh
2.2. Mathematical Model
2.2.1. General Equations
2.2.2. Boundary Conditions
2.2.3. Mathematical Description of Thermal and Electromagnetic Phenomena in Thin Films
2.3. Materials
3. Results
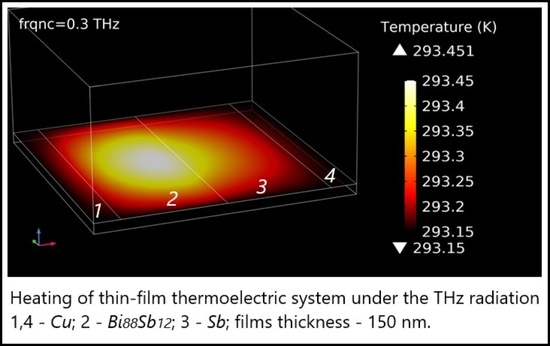
3.1. Temperature Distribution Along the Antenna Length
3.2. Temperature Difference and Responsivity
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| TE | Thermoelectric |
| THz | Terahertz |
| Sb | Antimony |
| Bi | Bismuth |
| Ni | Nickel |
References
- Zaytsev, K.I.; Kudrin, K.G.; Koroleva, S.A.; Fokina, I.N.; Volodarskaya, S.I.; Novitskaya, E.V.; Yurchenko, S.O. Medical diagnostics using terahertz pulsed spectroscopy. Phys. Conf. Ser. 2014, 486, 012014. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Zhao, X.; Yang, K.; Liu, Y.; Liu, Y.; Fu, W.; Luo, Y. Biomedical applications of terahertz spectroscopy and imaging. Trends Biotechnol. 2016, 34, 810–824. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.; Son, J.-H. Terahertz Imaging and Tomography Techniques. In Terahertz Biomedical Science and Technology; Son, J.-H., Ed.; CRC Press: Boka Raton, FL, USA, 2014; p. 47. [Google Scholar]
- Hoshina, H.; Sasaki, Y.; Hayashi, A.; Otani, C.; Kawase, K. Noninvasive mail inspection system with terahertz radiation. Appl. Spectrosc. 2009, 63, 81–86. [Google Scholar] [CrossRef] [PubMed]
- Federici, J.F.; Schulkin, B.; Huang, F.; Gary, D.; Barat, R.; Oliveira, F.; Zimdars, D. THz imaging and sensing for security applications—explosives, weapons and drugs. Semicond. Sci. Tech. 2005, 20, 266–280. [Google Scholar] [CrossRef]
- Malhotra, I.; Jha, K.R.; Singh, G. Terahertz antenna technology for imaging applications: A technical review. Int. J. Microw. Wirel. T. 2018, 10, 271–290. [Google Scholar] [CrossRef]
- Sizov, F.; Rogalski, A. THz detectors. Prog. Quant. Electron. 2010, 34, 278–347. [Google Scholar] [CrossRef]
- Rowe, D.M. General Principles and Basic Considerations. In Thermoelectrics Handbook; Rowe, D.M., Ed.; CRC Press: Boka Raton, Fl, USA, 2006; pp. 1-1–1-2. [Google Scholar]
- Yan, J.; Liao, X.; Yan, D.; Chen, Y. Review of Micro Thermoelectric Generator. J. Microelectromechanical Syst. 2018, 27, 1–18. [Google Scholar] [CrossRef]
- Basko, D. A photothermoelectric effect in graphene. Science 2011, 334, 610–611. [Google Scholar] [CrossRef] [Green Version]
- Buscema, M.; Barkelid, M.; Zwiller, V.; van der Zant, H.S.; Steele, G.A.; Castellanos-Gomez, A. Large and tunable photothermoelectric effect in single-layer MoS2. Nano Lett. 2013, 13, 358–363. [Google Scholar] [CrossRef] [Green Version]
- Yan, Y.; Liao, Z.M.; Ke, X.; Van Tendeloo, G.; Wang, Q.; Sun, D.; Yu, D.P. Topological surface state enhanced photothermoelectric effect in Bi2Se3 nanoribbons. Nano Lett. 2014, 14, 4389–4394. [Google Scholar] [CrossRef]
- Huang, D.; Zou, Y.; Jiao, F.; Zhang, F.; Zang, Y.; Di, C.A.; Zhu, D. Interface-Located Photothermoelectric Effect of Organic Thermoelectric Materials in Enabling NIR Detection. ACS Appl. Mater. Inter. 2015, 7, 8968–8973. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Cai, X.; Sushkov, A.B.; Suess, R.J.; Jadidi, M.M.; Jenkins, G.S.; Nyakiti, L.O.; Murphy, T.E. Sensitive room-temperature terahertz detection via the photothermoelectric effect in graphene. Nat. Nanotechnol. 2014, 9, 814–819. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, X.; Fujimura, N.; Lloyd, J.M.; Erickson, K.J.; Talin, A.A.; Zhang, Q.; Léonard, F. Carbon nanotube terahertz detector. Nano Lett. 2014, 14, 3953–3958. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.; Liu, Z.; Ren, Z. Size effect in thermoelectric materials. NPJ Quantum Mater. 2016, 1, 1–9. [Google Scholar] [CrossRef]
- Mele, P.; Narducci, D.; Ohta, M.; Biswas, K.; Morante, J.; Saini, S.; Endo, T. Masayuki Takashiri Thin Films of Bismuth-Telluride-Based Alloys. In Thermoelectric thin Films; Springer Nature Switzerland: Cham, Switzerland, 2019; pp. 1–29. [Google Scholar]
- Volklein, F.; Kessler, E. Thermoelectric properties of Bi1–xSbx films with 0< x < 0.3. Thin Solid Film. 1990, 155, 197–208. [Google Scholar]
- Suslov, M.V.; Komarov, V.A.; Suslov, A.V. Thermoelectric power of Bi92 Sb8 and Bi85 Sb15 thin films. Semiconductors 2017, 51, 862–865. [Google Scholar] [CrossRef]
- Cho, S.; DiVenere, A.; Wong, K.G.; Ketterson, B.J. Thermoelectric transport properties of n-doped and p-doped Bi0.91Sb0.09 alloy thin films. J. Appl. Phys. 1999, 85, 3655–3660. [Google Scholar] [CrossRef]
- Linseis, V.; Volklein, F.; Reith, H.; Huhne, R.; Schnatmann, L.; Nielsch, K.; Woias, P. Thickness and temperature dependent thermoelectric properties of Bi87Sb13 nanofilms measured with a novel measurement platform. Semicond. Sci. Technol. 2018, 33, 085014. [Google Scholar] [CrossRef]
- Völklein, F.; Kessler, E. Thermal Conductivity and Thermoelectric Figure of Merit of Thin Antimony Films. Phys. Status Solidi B 1990, 158, 521–529. [Google Scholar] [CrossRef]
- Zemskov, V.S.; Belaya, A.D.; Beluy, U.S.; Kozhemyakin, G.N. Growth and investigation of thermoelectric propertiesof Bi-Sb alloy single crystals. J. Cryst. Growth 2000, 212, 161–166. [Google Scholar] [CrossRef]
- Brandt, N.B.; Svistova, E.A. Uspekhi Phizich. Nauk 1970, 101, 249–272. (In Russian) [Google Scholar]
- Benia, H.M.; Straser, C.; Kern, K.; Ast, C.R. Surface band structure of Bi(1-x)Sbx (111). Phys. Rev. B 2015, 91, 161406. [Google Scholar] [CrossRef] [Green Version]
- Ihring, A.; Kessler, E.; Dillner, U.; Haenschke, F.; Schinkel, U.; Schubert, M.; Meyer, H.G. High performance uncooled THz sensing structures based on antenna-coupled air-bridges. Microelectron. Eng. 2012, 98, 512–515. [Google Scholar] [CrossRef]
- Huhn, A.K.; Spickermann, G.; Ihring, A.; Schinkel, U.; Meyer, H.G.; Haring Bolivar, P. Uncooled antenna-coupled terahertz detectors with 22 μs response time based on BiSb/Sb thermocouples. Appl. Phys. Lett. 2013, 102, 121102. [Google Scholar] [CrossRef] [Green Version]
- Mastel, S.; Lundeberg, B.M.; Alonso-Gonzalez, P.; Yuanda, G.; Watanabe, K.; Taniguchi, T.; Hone, J.; Koppens, H.L.F.; Nikitin, A. Terahertz Nanofocusing with Cantilevered Terahertz-Resonant Antenna Tips. Nano Lett. 2017, 17, 6526–6533. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, D.; Wang, Y.; Xiong, B.; Li, T. MEMS-based thermoelectric infrared sensors: A review. Front. Mech. Eng. 2017, 12, 557–566. [Google Scholar] [CrossRef]
- Grabov, V.M.; Komarov, V.A.; Kablukova, N.S. Galvanomagnetic Properties of Thin Films of Bismuth and Bismuth–Antimony Alloys on Substrates with Different Thermal Expansions. Phys. Solid State 2016, 58, 605–611. [Google Scholar] [CrossRef]
- Tinkham, M. Energy gap interpretation of experiments on infrared transmission through superconducting films. Phys. Rev. 1956, 104, 245–246. [Google Scholar] [CrossRef]
- Stefan, A. Maier Plasmonics: Fundamential and Applications; Springer: Berlin, Germany, 2007; p. 223. [Google Scholar]











| Material | Thermal Conductivity, in-Plane, | Thermal Conductivity, Cross-Plane, | Heat Capacity, | Density, |
|---|---|---|---|---|
| W·mK | W·mK | J·kgK | kg·m | |
| Sb | 63.24 | 24.43 | 207 | 6691 |
| 13.21 | 5.1 | 124 | 9790 | |
| mica | 5.1 | 0.51 | 880 | 2900 |
| Cu | 401 | 401 | 384 | 8960 |
| Frequency, THz | Re | Im |
|---|---|---|
| 0.1 | −6219.67 | 2.70 × 10 |
| 0.2 | −6219.42 | 1.35 × 10 |
| 0.3 | −6218.99 | 9.00 × 10 |
| 0.4 | −6218.39 | 6.75 × 10 |
| 0.5 | −6217.62 | 5.40 × 10 |
| 0.6 | −6216.68 | 4.50 × 10 |
| 0.7 | −6215.58 | 3.86 × 10 |
| 0.8 | −6214.3 | 3.37 × 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tukmakova, A.S.; Asach, A.V.; Novotelnova, A.V.; Tkhorzhevskiy, I.L.; Kablukova, N.S.; Demchenko, P.S.; Zaitsev, A.D.; Khodzitsky, M.K. FEM Simulation of THz Detector Based on Sb and Bi88Sb12 Thermoelectric Thin Films. Appl. Sci. 2020, 10, 1929. https://doi.org/10.3390/app10061929
Tukmakova AS, Asach AV, Novotelnova AV, Tkhorzhevskiy IL, Kablukova NS, Demchenko PS, Zaitsev AD, Khodzitsky MK. FEM Simulation of THz Detector Based on Sb and Bi88Sb12 Thermoelectric Thin Films. Applied Sciences. 2020; 10(6):1929. https://doi.org/10.3390/app10061929
Chicago/Turabian StyleTukmakova, Anastasiia S., Alexei V. Asach, Anna V. Novotelnova, Ivan L. Tkhorzhevskiy, Natallya S. Kablukova, Petr S. Demchenko, Anton D. Zaitsev, and Mikhail K. Khodzitsky. 2020. "FEM Simulation of THz Detector Based on Sb and Bi88Sb12 Thermoelectric Thin Films" Applied Sciences 10, no. 6: 1929. https://doi.org/10.3390/app10061929
APA StyleTukmakova, A. S., Asach, A. V., Novotelnova, A. V., Tkhorzhevskiy, I. L., Kablukova, N. S., Demchenko, P. S., Zaitsev, A. D., & Khodzitsky, M. K. (2020). FEM Simulation of THz Detector Based on Sb and Bi88Sb12 Thermoelectric Thin Films. Applied Sciences, 10(6), 1929. https://doi.org/10.3390/app10061929