Non-REM Sleep Marker for Wearable Monitoring: Power Concentration of Respiratory Heart Rate Fluctuation

Featured Application

This study proposes a new bio-signal marker that could be used for estimating non-REM sleep periods from nighttime heartbeat signals obtained by wearable electrographic and pulse wave sensors.

Abstract

A variety of heart rate variability (HRV) indices have been reported to estimate sleep stages, but the associations are modest and lacking solid physiological basis. Non-REM (NREM) sleep is associated with increased regularity of respiratory frequency, which results in the concentration of high frequency (HF) HRV power into a narrow frequency range. Using this physiological feature, we developed a new HRV sleep index named Hsi to quantify the degree of HF power concentration. We analyzed 11,636 consecutive 5-min segments of electrocardiographic (ECG) signal of polysomnographic data in 141 subjects and calculated Hsi and conventional HRV indices for each segment. Hsi was greater during NREM (mean [SD], 75.1 [8.3]%) than wake (61.0 [10.3]%) and REM (62.0 [8.4]%) stages. Receiver-operating characteristic curve analysis revealed that Hsi discriminated NREM from wake and REM segments with an area under the curve of 0.86, which was greater than those of heart rate (0.642), peak HF power (0.75), low-to-high frequency ratio (0.77), and scaling exponent α (0.77). With a cutoff >70%, Hsi detected NREM segments with 77% sensitivity, 80% specificity, and a Cohen’s kappa coefficient of 0.57. Hsi may provide an accurate NREM sleep maker for ECG and pulse wave signals obtained from wearable sensors.

1. Introduction

Sleep shows dynamic physiological conditions that differ from those during waking. The cardiac rhythm during sleep is modulated by sleep stages, mainly by the periodic appearance of non-REM (NREM) and REM stages that involve switching between two different autonomic states [1,2,3,4]. The cardiac rhythm during sleep could be also affected by pathological phenomena peculiar to sleep, such as sleep disordered breathing (SDB), that causes characteristic heart rate pattern known as cyclic variation of heart rate [5,6]. To interpret arrhythmias or other electrocardiographic (ECG) phenomena observed during ambulatory ECG monitoring with wearable sensors, it is often necessary to estimate the period of sleep and preferably, the distributions of sleep stages. For these purposes, many methods using the analyses of heart rate variability (HRV) [7,8,9,10,11] and/or actigraphic body movement (ABM) [12,13,14,15] have been reported. However, their univariate accuracies for estimating the period of sleep and sleep stages are modest and they have no definitive physiological basis by which they can distinguish sleep from awake rest.

To resolve this problem, we developed a new HRV sleep index named Hsi that detects NREM sleep periods based on the physiological features of cardiorespiratory regulations during sleep. It is well known that the regularity of respiration increases during NREM sleep. Respiration modulates heart rate and generates high frequency (HF, 0.15–0.45 Hz) components of HRV at the frequency of respiration. Consequently, as the regularity of the respiratory cycle increases, the power of the HF component concentrates on a narrower frequency band. We therefore developed Hsi to measure the degree of HF power concentration. Then, we examined the performance of Hsi for discriminating NREM sleep from wake and REM stages and compared it with the performances of conventional indices of HRV and ABM.

2. Materials and Methods

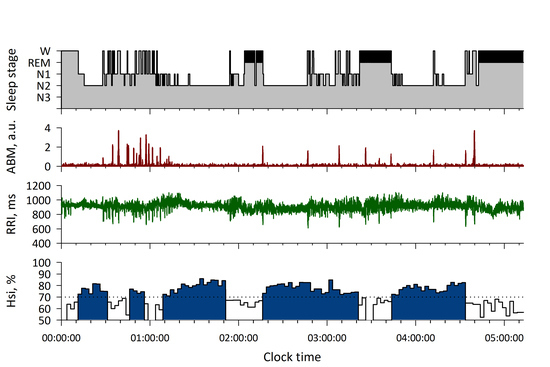
2.1. Measurement of HF Power Concentration

We developed a new HRV sleep indicator named Hsi, which quantifies frequency regularity of respiration. Hsi can be calculated from time series of any bio-signal showing respiratory fluctuation, such as R-R intervals, pulse intervals, blood pressure, and respiration itself.

The computation of Hsi starts with power spectrum of bio-signal (Figure 1a). First, the algorithm detects the highest spectral peak within HF frequency band (0.15–0.45 Hz), defines its frequency as F_m, and calculates total power within the frequency range of F_m ± L/2 as S_L,

$$S_L={\displaystyle {{\displaystyle \int }}_{F_m-L/2}^{F_m+L/2}}P\left(f\right) df$$

(1)

where P(f) is power spectral density and L is a constant value of frequency (in this study, we used L = 0.14 Hz). Second, total power S_ω within the frequency band of F_m ± ω/2 is calculated as the function of ω, where ω is the frequency rage centered at F_m.

$$S_{\omega }={\displaystyle {{\displaystyle \int }}_{F_m-\omega /2}^{F_m+\omega /2}}P\left(f\right) df (0<\omega <L)$$

(2)

Third, R_ω is calculated as the ratio of S_ω to S_L.

$$R_{\omega }(\%)=100\times \frac{S_{\omega }}{S_L}$$

(3)

Then, Hsi is calculated as area under the curve (AUC) of R_ω (Figure 1b)

$$\mathrm{Hsi}(\%)=\frac{1}{L}{\displaystyle {{\displaystyle \int }}_0^L}{R}_{\omega }d\omega$$

(4)

2.2. Subjects’ Characteristics

The present study was performed according to the protocol that was approved by the Institutional Review Board of Nagoya City University Graduate School of Medical Sciences and Nagoya City University Hospital, Japan (No. 60160097).

We used anonymized polysomnographic data provided by Gifu Mates Sleep Clinic (Gifu city, Gifu, Japan). The data were obtained from consecutive 141 subjects who underwent screening overnight polysomnography for sleep disorders. The characteristics of subjects are shown in

Table 1. Characteristics of subjects.

N	141
Age, year	46 (33–58)
Male/female	103/38
Time in bed (TIB), min	475 (460–485)
Sleep period time (SPT), min	460 (428–472)
Total sleep time (TST), min	376 (318–410)
Sleep latency, min	10 (6–20)
Non-REM period, min	301 (261–322)
REM period, min	73 (52–96)
REM latency after sleep onset, min	95 (70–137)
Wake period during SPT, min	79 (44–107)
Sleep efficiency, %	83 (74–90)
AHI (TIB)	0.8 (0.1–6.9)
AHI (TST)	1.0 (0.1–9.5)
AHI (TIB) > 15/h	19 (13%)
Hsi > 65% period, min	290 (180–340)
Mean Hsi, %	67 (62–70)

Data are medians (IQR).

. Among 141 subjects, 33 subjects were normal, 83 had mild SDB with an apnea-hypopnea index (AHI) of <15/h, 19 had moderate-to-severe SDB with an AHI ≥ 15/h, 3 had parasomnia, and 3 had restless leg syndrome. None of the subjects had atrial fibrillation or pacemaker implantation. In all subjects, ECG of the polysomnographic data was in sinus rhythm for >90% of the entire data length.

2.3. Measurements

The polysomnograms were obtained using the Alice Diagnostic Sleep System (Philips Respironics, The Netherlands). The sleep stages per 30-s epoch, respiratory events, and periodic leg movement were scored using the standard diagnostic criteria of the American Academy of Sleep Medicine and a published criterion [16] by registered polysomnogram technicians.

Actigraphic data were recorded simultaneously with polysomnograms by a wrist acceleration sensor (HFM-3D Prototype, Suzuken Co., Nagoya, Japan), which digitized 3-axis acceleration data at 31.25 Hz and stored. Acceleration signals in x, y, and z axes were bandpass filtered (0.02–0.08 Hz) to remove baseline trend and high-frequency noise and were composed into the magnitude as Act(t) with the following equation:

$$\mathrm{Act}\left(t\right)=\sqrt{x{\left(t\right)}^2+y{\left(t\right)}^2+z{\left(t\right)}^2}$$

(5)

Single-lead ECG data were extracted from the polysomnograms with a sampling frequency of 500 Hz. The ECG signals were scanned on a personal computer using a customized beat-detection and beat-classification algorithm that identified the temporal position of all QRS complexes and labeled the beats as normal (sinus), ventricular ectopic, supraventricular ectopic, atrial fibrillation, and artifact.

For supplementary analysis, respiratory signal was also extracted from thoracic movement digitized at 100 Hz.

2.4. Data Analysis

R-R interval, ABM, and respiration time series data were divided into consecutive 5-min segments for the entire length, so that each segment includes 10 consecutive 30-s epochs used for sleep stage coding. Then, the sleep stage of segment was defined as those of the majority among 10 epochs, i.e., if the stage of ≥ 6epochs were the same, it was chosen as the stage of the segment. If there was no majority stage among 10 epochs, the segments were defined as transitional stages. In each 5-min segment, the maximum value of Act(t) were selected as ABM of the segment.

R-R intervals in each segment were interpolated with a step function only using interval data consisting of consecutive normal beats and the interpolated signal was resampled at 1024 equidistant time points. After calculating heart rate from mean R-R interval, the resampled R-R interval time series were filtered with a Hanning window and converted into frequency domain by fast Fourier transformation. From the obtained power spectrum, Hsi was computed for each segment. After correcting for the losses of variance resulting from the sampling and filtering processes, the power of the very-low-frequency (VLF, 0.0033–0.14 Hz), low-frequency (LF, 0.04–0.15 Hz), and HF components and LF-to-HF ratio were computed. Additionally, the peak power of HF component was also calculated. The power of LF and HF components and peak HF power were transformed into the natural logarithmic values. As an index of nonlinear heart rate dynamics, scaling exponents (α) were calculated by detrended fluctuation analysis [17,18]. According to earlier studies [8,9], we measured scaling exponents in the ranges of 30–60 s and 60–300 s as α_30–60 and α_60–300, respectively, so that they fit to 5-min segment lengths.

Additionally, power spectrum of respiration was also calculated for each 5-min segment and the Hsi of respiration signal was also calculated in the same ways as that of the R-R intervals.

2.5. Statistical Analysis

We used program package of Statistical Analysis System (SAS Institute, Cary, NC, USA) for statistical analyses. The difference in Hsi with sleep stage was evaluated by mixed model of ANOVA in which age, sex, and AHI were treated as the fixed effects and subject as random effects. We evaluated the performance of Hsi, ABM, and indices of HRV and heart rate dynamics for discriminating NREM segments from wake and REM segments. The discriminatory performance was evaluated with AUC of receiver-operating characteristic (ROC) curve analysis. The significance of differences in AUC between indices were evaluated with Hanley and McNeil’s method [19]. The discriminatory performance of indices with cutoff thresholds was evaluated with the sensitivity, specificity, accuracy, and Cohen’s kappa coefficient of agreement. The discriminant analysis was performed for both the dominant sleep stage per 5-min segment and the sleep stage per 30-sec epoch. Statistical significance was considered for p < 0.05.

3. Results

Figure 2 shows a hypnogram in a representative subject at the onset of sleep. As the sleep stage changes from wake to NREM sleep, large ABM disappears, a sharp HF peak appears in R-R interval power spectrum, and Hsi increases above 70%. Figure 3 is an all-night hypnogram in another representative subject. While Hsi is below 70% during wake and REM sleep periods, it exceeds 70% in synchrony with NREM sleep periods.

From 141 subjects, a total of 11,636 segments of data were obtained, including 2261 (17.1%) awake, 6891 (52.2%) NREM, 2484 (18.8%) REM, and 1578 (11.9%) transitional segments. The average values of the HRV indices, scaling exponents, and ABM for each stage are shown in Figure 4 and

Table 2. Sleep stage and indices of heart rate variability (HRV).

HRV Indices	Stage W N = 2261 17.1%	Stage NREM N = 6891 52.2%	Stage REM N = 2484 18.8%	Transitional N = 1578 11.9%	p
Heart rate, bpm	67.7 ± 10.3	60.7 ± 9.2	62.1 ± 8.8	63.6 ± 9.4	<0.0001
VLF power, ln(ms2)	6.80 ± 1.45	6.03 ± 1.33	7.48 ± 1.19	7.29 ± 1.39	<0.0001
LF power, ln(ms2)	5.54 ± 1.43	5.61 ± 1.28	6.17 ± 1.22	6.15 ± 1.25	<0.0001
HF power, ln(ms2)	4.73 ± 1.45	5.77 ± 1.34	5.41 ± 1.39	5.47 ± 1.31	<0.0001
HF peak power, ln(ms2)	8.03 ± 1.57	9.75 ± 1.48	8.75 ± 1.53	8.88 ± 1.46	<0.0001
LF/HF	3.36 ± 3.35	1.30 ± 1.54	3.21 ± 3.42	2.86 ± 2.73	<0.0001
α30–60	1.25 ± 0.27	0.96 ± 0.30	1.28 ± 0.27	1.26 ± 0.27	<0.0001
α60–300	0.99 ± 0.34	0.77 ± 0.26	1.01 ± 0.29	0.91 ± 0.32	<0.0001
Hsi of respiration, %	67.6 ± 9.2	78.7 ± 7.9	66.4 ± 7.7	68.9 ± 8.8	<0.0001

Data are mean ± SD. N = number of 5-min epochs, VLF = very low frequency, LF = low frequency, HF = high frequency, LF/HF = LF-to-HF power ratio.

. As shown in Figure 4, Hsi was greater during NREM stage than during wake, REM, and transitional stages (p < 0.0001) and ABM was greater during wake stage than NREM and REM stages (p < 0.0001). As shown in Table 2, VLF power, LF/HF, α_30–60, and α_60–300 were lower and HF and HF peak power was greater during NREM stage than during wake and REM stage, heart rate, (p < 0.0001 for all).

Mixed-model ANOVA revealed that the difference in Hsi between NREM and other stages was significant even after adjusting for the effects of age, sex, and AHI (p < 0.0001). Age and AHI had no significant effect on Hsi, although Hsi was greater in females (least-square mean [SE], 65.9 [0.7]%) than males (64.1 [0.4]%, p = 0.038).

ROC curve analysis for the dominant stage per 5-min segment revealed that the performance of Hsi for discriminating NREM from wake and REM stages was significantly greater than those of other HRV indices, scaling exponents, and ABM (

Table 3. Discriminant performance of NREM stage from wake and REM stages per 5-min segment.

Variable	AUC (SE)	95%CI	P vs. Hsi	Cut off	Sens %	Spec %	Acc
Hsi	0.86 (0.0034)	0.86–0.87	-	>70%	77	80	79
Heart rate	0.64 (0.0051)	0.63–0.65	<0.0001	<64 bpm	69	53	62
VLF power	0.71 (0.0048)	0.70–0.72	<0.0001	<6.57 ln(ms2)	68	65	67
LF power	0.54 (0.0054)	0.53–0.55	<0.0001	<6.16 ln(ms2)	65	43	56
HF power	0.66 (0.0051)	0.65–0.66	<0.0001	>5.18 ln(ms2)	70	55	64
HF peak power	0.75 (0.0047)	0.75–0.76	<0.0001	>9.16 ln(ms2)	69	70	69
LF/HF	0.77 (0.0043)	0.76–0.78	<0.0001	<1.27	68	72	70
α30–60	0.77 (0.0044)	0.76–0.78	<0.0001	<1.13	70	70	70
α60–300	0.72 (0.0078)	0.71–0.73	<0.0001	<0.88	71	64	68
ABM	0.79 (0.0043)	0.78–0.79	<0.0001	<0.6 a.u.	80	70	76
Hsi of respiration	0.85 (0.0043)	0.85–0.86	0.45	>70%	76	81	78

AUC (SE) = area under the receiver-operating characteristic curve (standard error), CI = confidence interval, Sens = sensitivity, Spec = specificity, Acc = accuracy.

and Figure 5). Particularly, the performance of Hsi was greater than that of HF peak power, indicating the importance of the sharpness rather than the height of HF peak. When Hsi > 70% was used as a cutoff, Hsi detected NREM sleep with 77% sensitivity, 80% specificity, 79% accuracy, and a Cohen’s kappa coefficient of 0.57 (95%CI, 0.55–0.58). The discriminant performance of Hsi was preserved (AUC = 0.87) even in the separated analysis of 19 subjects with moderate-to-severe SDB (AHI, 26.0 [21.7–44.5/h]).

Since Hsi was considered to reflect the regularity of respiration frequency, we compared the discriminant performance of Hsi calculated from the R-R interval and respiration itself. Like the Hsi of R-R interval, the Hsi of respiration was greater during NREM stage than during wake, REM, and transitional stages (p < 0.0001, Table 2). The discrimination performance of Hsi of respiration (AUC = 0.85), however, was comparable to that of Hsi of R-R interval (Table 3 and Figure 5).

ROC curve analysis for the sleep stage per 30-s epoch revealed similar results (

Table 4. Discriminant performance of NREM stage from wake and REM stages per epoch.

Variable	AUC (SE)	95%CI	p vs. Hsi
his	0.79 (0.0031)	0.78–0.79	-
Heart rate	0.54 (0.0036)	0.53–0.55	<0.0001
VLF power	0.69 (0.0032)	0.68–0.69	<0.0001
LF power	0.56 (0.0036)	0.56–0.57	<0.0001
HF power	0.61 (0.0036)	0.61–0.62	<0.0001
HF peak power	0.70 (0.0035)	0.69–0.70	<0.0001
LF/HF	0.74 (0.0030)	0.73–0.74	<0.0001
α30–60	0.76 (0.0029)	0.76–0.77	<0.0001
α60–300	0.63 (0.0034)	0.63–0.64	<0.0001
ABM	0.76 (0.0028)	0.76–0.77	<0.0001

). Although the AUC of Hsi was lower than that for 5-min segment analysis, it was still significantly greater than those of other HRV indices, scaling exponents, and ABM.

4. Discussion

In this study, we proposed a new sleep indicator named Hsi that reflects the regularity of respiratory frequency by quantifying the degree of HF power concentration on a narrow frequency range. In the analysis of polysomnographic data in 141 subjects, we observed that Hsi discriminates NREM sleep from wake and REM sleep segments with an AUC of ROC curve of 0.86, which was significantly greater than those of other HRV indices, scaling exponents, and ABM that have been used as indicators to detect sleep or estimate sleep stages in earlier studies [7,8,9,10,11,12,13,14,15]. With a cutoff criterion of > 70%, Hsi detected NREM sleep with 77% sensitivity, 80% specificity, 79% accuracy, and a Cohen’s kappa coefficient of 0.57. These observations indicate that Hsi is a powerful univariate marker of NREM sleep. Hsi is expected to improve the performance of sleep and sleep stage estimations by R-R intervals of ECG and other heartbeat signals obtained by wearable sensors.

There are a plenty of earlier studies on the estimations of sleep and sleep stage using ECG [8,9,10,11]. In a study of 78 subjects undergoing polysomnography, Penzel et al. [8] analyzed HRV indices (mean R-R interval, SD of R-R interval, VLF, LF, HF, and LF/HF) and scaling exponents for 5-min consecutive segments whose sleep stage was defined as that continued for >3 min in the segment. They reported 85% accuracy for sleep stage separation by a discriminant model consisting of mean and SD of R-R intervals and scaling exponents. In a study using 18 polysomnographic data in the MIT/BIH Polysomnographic Database, Adnane et al. [9] reported 80% accuracy and a Cohen’s kappa of 0.41 for the classification of wake and sleep of 30-s epochs with the 10 features of HRV and heart rate dynamics selected by the support vector machine recursive elimination system. In a study of 48 polysomnographic data in healthy adults, Fonseca et al. [10] reported 80% accuracy and a kappa of 0.56 in the classification of 30-s epochs of wake, NREM sleep, and REM sleep with 80 features selected from 142 feature of ECG and thoracic respiratory effort. Finally, in a study of 20 young healthy subjects, Singh et al. [11] reported 76% accuracy and a kappa of 0.52 for the classification of 5-min segment of REM and NREM sleep by HRV and nonlinear heart rate dynamics. Although the discriminant accuracy of Hsi we observed in this study seems comparable to those reported in these earlier studies, it should be noted that Hsi achieved that with a univariate model, while those in earlier studies were achieved by multivariate models. This suggests that the discriminant performance may be further improved by combination of Hsi and other indices. In fact, we observed that ABM effectively distinguishes between REM and wake stages after NREM had been separated by Hsi, suggesting the usefulness of the combination of Hsi and ABM for the classification of wake, NREM, and REM stages (Figure 4).

Hsi has strengths that are not observed in other HRV indices, respiration signal, or ABM. First, Hsi quantifies the spectral shape of HF component independently of its power. This seems advantageous over indices reflecting the power of HRV that is strongly dependent on age [20], respiratory frequency [21], and health states affecting autonomic function [22]. In fact, we observed that the discriminant performance of Hsi was independent of age and AHI. Second, Hsi was developed on the solid physiological basis that respiratory regularity increases with NREM sleep. In contrast, the autonomic indices of HRV and ABM are based on indirect or relative relationships. Although autonomic functions and heart rate dynamics are known to differ with sleep stage [3,7], the changes of these metrics from wake to sleep are continuous but not discrete, and there is no convincing physiological basis supporting for their ability to distinguish light sleep from awake rest.

If Hsi reflects respiratory regularity, it may be speculated that respiration regularity measured directly from respiration signals may indicate better discriminant power of NREM stage than Hsi obtained from ECG. To examine this hypothesis, we calculated Hsi from the power spectrum of respiration. We observed, however, that the discriminant performance of the Hsi of respiration did not exceed that of Hsi of R-R interval. Although the exact mechanisms deserve further studies, a possible mechanism is that the measurements of respiration signal could be affected by noises from sources including body movements and external air flow, while respiratory fluctuation in heart rate is caused by intrinsic central neural mechanisms [23] that may be less affected by such disturbances. This may support for the use of ECG or other heartbeat signals from wearable devices for calculating Hsi.

Hsi seems to provide a useful indicator of sleep for both clinical and health promotion fields. Because the cardiac autonomic functions are modulated by sleep and sleep stages [1,2,4], the information of sleep period and sleep stage during Holter ECG monitoring are apparently useful for investigating the mechanisms of arrhythmias and other transient phenomena that show heterogeneous temporal distributions during the day. Information on sleep period is also important for ECG screening for sleep-related pathological phenomena such as SDB. SDB can be effectively screened by cyclic variation of heart rate that accompanies the episodes of sleep apnea [5,6]. Without the information of sleep period, however, it is hard to determine whether a patient does not have SDB or has not slept when the cyclic variation is not observed. In health promotion fields, due to the widespread use of wearable sensors, beat-to-beat heart rate or pulse rate data during daily life are being accumulated as big data. Along with this, the demands for automated algorithms to evaluate health indicators are rising. Hsi seems to provide a powerful and indispensable element for such methods to estimate sleep period and sleep stages from heart rate and pulse rate big data.

A limitation of this study is that the dependency of discriminant accuracy on the length of data segment. In this study, consecutive 10 sleep stages were grouped into one 5-min segment for which Hsi was calculated, although sleep stages were determined every 30-s epochs in polysomnography. In a supplementary study in a group of healthy subjects, we have observed the discriminant accuracy of NREM sleep by Hsi is affected by the length of segment; AUCs of discriminant performance of Hsi were 0.88, 0.84, and 0.80 for segment length of 5, 3, and 2 min, respectively (Figure S1). Therefore, we also examined the performance of 5-min segment His to discriminate the sleep stage of 30-s epoch. As expected, the discriminant performance of all indices including Hsi reduced, although Hsi still showed the best performance among them. The temporal resolution and the accuracy of sleep stage are in a trade-off relationship. Another possible limitation is the effects of SDB on Hsi. Although we observed that the discriminant performance of Hsi was preserved even in 19 subjects with moderate-to-severe SDB (AUC = 0.87), more than half of them had moderate SDB (AHI, 26.0 [21.7–44.5/h]). Given that Hsi reflects the regularity of respiratory frequency, further studies are required for the impacts of SDB on Hsi and its effectiveness as a sleep indicator in patients with severe SDB.

5. Conclusions

We developed a novel sleep indicator named Hsi that reflects the degree of power concentration of HF component of HRV. Hsi has a greater performance in the discrimination of NREM sleep from awake and REM sleep than conventional HRV indices, scaling exponents of heart rate dynamics, and ABM. Hsi is expected to contribute accurate estimation of sleep stage by ambulatory ECG and other heartbeat signals obtained by wearable sensors.

6. Patents

Hsi is pending as Japanese Patent Application No. 2017-061892.