FEM-CFD Simulation and Experimental Study of Compound Parabolic Concentrator (CPC) Solar Collectors with and without Fins for Residential Applications

Abstract

Compound parabolic concentrator (CPC) solar collectors are widely used for solar energy systems in industry; however, CPC collectors for residential applications have not been fully investigated. In this work, the thermal performance of non-tracking, small-size and low-cost CPC collectors with an absorber with and without segmented fins was studied experimentally and by means of a proposed numerical methodology that included ray tracing simulation and a coupled heat transfer finite element method (FEM)-computational fluid dynamics (CFD) simulation, which was validated with experimental data. The experimental results showed that the CPC with a finned absorber has better thermal performance than that of the CPC with absorber without fins, which was attributed to the increase in thermal energy on the absorber surface. The numerical results showed that ray tracing simulation can be used to estimate the heat flux on the absorber surface and the FEM-CFD simulation can be used to estimate the heat transfer from the absorber to the water running through the pipe along with its temperature. The numerical results showed that mass flow rate is an important parameter for the design of the CPC collectors. The numerical methodology developed in this work was capable of describing the thermal performance of the CPC collectors and can be used for the modeling of the thermal behavior of other CPCs solar systems.

1. Introduction

Today, the use of renewable energy sources for the generation of hot water for industrial and residential applications is rapidly increasing to meet climate change policies worldwide [1]. Among renewable resources, solar energy is of great interest because it is widely available, clean and free of cost. Solar energy can be used for many applications including power generation [2], heating systems [3], water treatment [4] and water heating [5,6]. Solar collectors capture solar energy and transform it into useful heat that can be employed to generate hot water. A compound parabolic concentrator (CPC) is a type of non-imaging collector [7] made of two reflective parabolic surfaces, which redirect the incident solar radiation onto the surface of an absorber placed at the focal points. The absorber can be flat or tubular [8]. The absorber heat is transferred, by conduction, to a heating pipe. If the absorber is a pipe, the absorber heat is transferred directly, by convection, to the circulating working fluid. The first CPC collector was designed by Winston [9,10]; since then, several improvements to the original design have been developed including the optimization of the geometry of the reflective surface to attain a maximum concentration ratio [11] (defined as the ratio of the aperture area to the absorber area), the improvement of the absorber by using evacuated tubes to surround the surface of the absorber to reduce heat loss [7] and the use of fins in the absorber to increase solar radiation absorption [12,13].

CPC collectors can be classified for low temperature (<100 °C), medium temperature (100–250 °C) and high temperature applications (>500 °C) [14]. Low temperature CPCs are used for residential applications including water and space heating. CPCs for residential applications have been widely studied [5]; however, many of the studied residential CPCs are large and heavy and include technological features to achieve higher temperatures and thermal efficiency. These features, such as evacuated tubes and tracking systems, increase the manufacturing and maintenance cost, which could be a problem for the use of CPCs in low income and remote areas.

Research on low cost and small size CPC collectors for residential applications is limited. Carrillo et al. [15] developed a methodology to manufacture inexpensive CPC solar collectors, which produced CPC reflective surfaces with an accuracy of 94% with respect to the ideal CPC surface shape. This methodology was then used by Terron et al. [16] to design and build a small size CPC solar collector with a tubular absorber and concentration ratio of 1.41, for residential applications, using low cost materials; they obtained an average thermal efficiency of ~43% using a fixed tilt angle of 21° on a winter day. Osorio et al. [17] reported a simplified low-tech design of a CPC collector with a concentration ratio of 1 and found that a reduction in the manufacturing cost is feasible, while obtaining an increase of 79 °C in the receiver stagnation temperature.

Most of the aforementioned studies on CPC collectors have been performed experimentally, which in some cases could be costly due to the manufacturing process to obtain an optimal design and/or the necessary equipment and instrumentation to monitor temperatures in the CPC system. Numerical modeling is a useful tool to complement experimental studies that have been employed to better understand solar collectors and improve their design. Benrejeb et al. [18] used ray tracing simulations to obtain the optical and thermal performance, along with the energy distribution around the absorber of a CPC to improve the geometry design of a solar water heater integrated with a CPC collector; they proposed a new system design, with an improved optical performance and a concentration ratio of 1.34, that reached a maximum temperature of 65 °C. Su et al. [19] developed a ray tracing model to analyze the thermal performance and efficiency of a CPC collector with a concentration ratio of 3.06. They found that their model predicted a maximum efficiency of ~57% with a relative error of less than 10%, when compared to the experimental results. Gunjo et al. [20] carried out computational fluid dynamics (CFD) simulations to investigate the thermal performance of a flat plate solar collector. They found that the CFD model could predict the outlet water and absorber temperatures with a maximum relative error of 5.4% and 2%, respectively, when compared to the experimental measurements. Badiei et al. [21] used CFD simulations to investigate the performance of a solar flat plate collector with fins integrated with a layer of phase-change material (PCM). They found that the average solar collector efficiency increased from 33% to 46% on a summer day when a PCM with a melting temperature of 35.4 °C was used. They also found that the incorporation of fins increased the storage capacity of the system. Korres and Tzivanidis [22] used ray tracing analysis and CFD simulations to study the thermal and optical performance of a CPC collector and to optimize its design. They found that temperature gain from the inlet to the outlet predicted by the simulations on a spring day only diverged by 6.7% on average from the experimental results. They also proposed a modified reflector geometry that improved the optical efficiency of the collector by 5.74%. Yuan et al. [23] employed ray tracing simulations to calculate the solar irradiance on the receiver of a CPC collector equipped with a transparent polymer foil. They also used CFD simulations to predict the temperature rises of the collector in the range of 20–81 °C with a relative error of less than 3.7%. They found that the installation of the foil increased the thermal efficiency of the CPC collector when compared to a collector without foil. Hassanzadeh et al. [24] combined an optical simulation with a finite element method (FEM) simulation to improve the design of a medium temperature non-tracking CPC collector with a pentagon absorber. They found experimentally that the solar collector had an optical efficiency of 64% and a thermal efficiency of 50% at 200 °C, and a stagnation temperature of 378 °C, which was also predicted by the numerical simulations. Carlini et al. [25,26] used FEM simulations to perform a heat transfer analysis on a CPC system, with solar cells, and with and without a cover, to optimize its geometry and increase the efficiency of the system. They found that the FEM simulations predicted the temperature, power and efficiency of the whole system with average discrepancies of less than 12% with respect to the experimental data. They also found that the best performing configuration was the uncovered CPC.

The motivation for this work is to contribute to the development of low-temperature (<100 °C), small-size, low-cost and low-maintenance CPC solar collectors for residential applications, and, at the same time, to develop a numerical methodology to assess the performance of this type of CPC collector using numerical tools to improve the CPC design. To achieve this, a small-size CPC solar collector for water heating with two different types of absorbers (with and without segmented fins) was tested experimentally to assess the thermal performance and to validate the numerical simulations. A numerical methodology is presented, which includes ray tracing modeling to obtain the incident radiation on the absorber surface, and a coupled thermal FEM-CFD numerical simulation to predict heat transfer from the absorber surface to the circulating water and its temperature. CPC collectors with three different types of absorbers (without fins, with segmented fins and with continuous fins) were assessed numerically.

2. Materials and Methods

2.1. Compound Parabolic Concentrator (CPC) Solar Collector

The non-tracking CPC collector used in this study is based on the CPC design presented in detail in a previous work [16]; however, a brief description of the CPC is provided here for the sake of completeness. Figure 1a shows the design of the CPC, which is composed of two reflective parabolic surfaces. The CPC has a width of 174 mm, a height of 78.5 mm, a length of 1.06 m (Figure 1b), a half-angle of acceptance of 45° and a concentration ratio of 1.41 [16]. A copper absorber tube with an internal diameter of 31.75 mm and a thickness of 1.6 mm was used (Figure 1a,b). The circulating fluid inside the absorber tube was water. A glass cover and insulation material were used to reduce heat loss (Figure 1a). The fixed tilt angle of the east–west aligned CPC collector (angle between the CPC axis of symmetry and the horizontal) was 32° to optimize power on the absorber surface in the winter season. Figure 1c shows a photograph of the CPC solar collector systems.

Two types of absorbers were used for the experiments, that is, a tubular absorber without fins (Figure 1b,d), and a tubular absorber with segmented fins (Figure 1e and Figure 2). In the latter, 19 copper fins were attached to the copper tube (10 on one side and 9 on the other side) (Figure 2). The fins had a length of 52 mm, height of 25.4 mm and a thickness of 3 mm (Figure 2). The fins were separated by a distance of 53 mm (Figure 2). Both absorbers were painted with matte black non-selective paint.

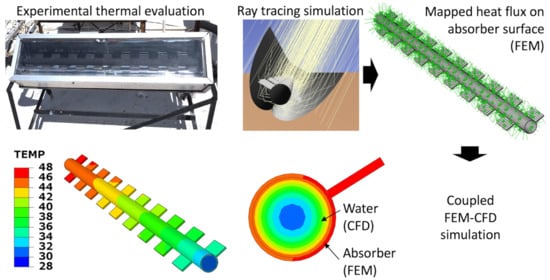
2.2. Experimental Settings

The CPC solar collector systems (Figure 1c) were located in the city of Merida, in the Yucatan Peninsula, Mexico (21.02° N, 89.63° W). The CPC was instrumented with K-type thermocouples (TT-K-20, accuracy of ±0.75%, Omega Engineering Inc., Norwalk, CT, USA) to measure the inlet, outlet and absorber temperatures. A calibration procedure was implemented for each thermocouple to reduce measurement uncertainty. The temperature of the air inside the CPC collector and the ambient temperature were also measured. A submersible pump WP350 (LAWN Industry, Atizapán de Zaragoza, Mexico) was used to produce a forced flow of ~0.36 L/min (0.0076 m/s). The flow was measured using a flow sensor Omega FLR1000 with an accuracy of ±1% (Omega Engineering Inc., Norwalk, CT, USA). The temperatures and flow data were wirelessly recorded with an acquisition frequency of 0.2 Hz using NI-9213 and NI-9207 modules, respectively, and a data acquisition system NI cDAQ-9191 (National Instruments Corp., Austin, TX, USA). Incident solar irradiance and ambient temperature were measured with a Davis Vantage Pro2 Plus weather station (Davis Instruments Corporation, Hayward, CA, USA) with an acquisition frequency of 0.017 Hz and accuracies of ±5% and ±0.3 °C, respectively. For this study, measurements were obtained on 1 March 2020 from 6 a.m. to 6 p.m. using two separate CPC collector systems operating simultaneously (Figure 1c), one with the absorber without fins (Figure 1d) and the other one with the absorber with segmented fins (Figure 1e and Figure 2).

2.3. Numerical Methodology

Figure 3 shows a schematic diagram of the numerical methodology used in this work to investigate the thermal performance of the CPC solar collectors described in Section 2.1. Firstly, an optical analysis is performed using the ray tracer software Tonatiuh [27] to obtain the energy and spatial distribution of rays (photons) intersecting the surface of the absorber tube, for a certain day, from 6 a.m. to 6 p.m. (Figure 3a). Secondly, the data from the ray-tracing analysis is processed using MATLAB [28] to obtain the energy distribution (surface heat flux) on the CPC absorber surface (Figure 3b). Thirdly, a coupled FEM-CFD simulation is built in Abaqus [29], in which the power (energy) is input on the absorber FEM model, which is coupled with the CFD model of the water running through the absorber (tube) (Figure 3c). The thermal FEM-CFD analysis allows for the estimation of the temperature of the water. Each step of the simulation methodology is described in detail in the following sections.

2.4. Optical Ray Tracing Simulation

An optical analysis was performed using the Monte Carlo-based ray tracer software Tonatiuh [27,30] to obtain the total irradiation (energy flux) that the CPC absorber surface receives at different times of the day. The Tonatiuh software was developed for optical simulations of solar concentrating systems and has been successfully used to simulate CPC solar collectors. The 3D geometry of both the reflector and absorber of the CPC collector was built in the Tonatiuh software (Figure 4). For the simulations, three different geometries were modeled, i.e., CPC collector without fins (Figure 4a), with segmented fins (Figure 4b) and with continuous fins (Figure 4c). The location for this numerical study was the city of Merida (Section 2.2), and the solar parameters were an angular distribution (pillbox) [16], an irradiation of 1000 W/m² and a total of 1 million rays for the analysis. The rays intersecting a surface are called photons. The output of the ray-tracing analysis is the coordinates of the intersection point on the absorber surface of each individual photon and its energy in tabular form. Figure 4d,e illustrate the photons intersecting the surface of the CPC collector with an absorber with segmented fins and a close-up view, respectively.

2.5. Data Processing of the Ray Tracing Analysis Using MATLAB

Figure 5a–c show plots created in MATLAB using the data that was obtained from the ray tracing analysis, in which the photons striking the surface of the CPC absorber without fins, with segmented fins and with continuous fins at a given time (12 p.m. on 1 March 2020) are shown. To obtain the energy flux distribution on the surface of the absorber without fins, a code written in MATLAB was used to divide the surface area of the absorber into 80 sections. The photons striking each individual section per hour were counted. In this way, the irradiation (energy per unit area per unit time) in each individual section was obtained. This can be seen in Figure 5d, in which the energy flux (W/m²) in each individual section of the absorber area is depicted. The data shown in Figure 5d was subsequently exported to the software Abaqus to map the energy flux onto the surface of the absorber in the FEM model. Similarly, to obtain the energy flux on the absorber with segmented fins (Figure 5e) and the absorber with continuous fins (Figure 5f), the absorber surface, which included the tube and fins surfaces, was divided into 118 and 120 sections, respectively.

2.6. Coupled FEM-CFD Model in Abaqus

Figure 6a shows the meshes of both FEM and CFD models used for the coupled FEM-CFD co-simulation of the absorber without fins. This type of simulation allows conjugate heat transfer between the FEM model of the solid tube (absorber) built in Abaqus/Standard and the CFD model of the water running inside the absorber built in Abaqus/CFD. Abaqus/Standard and Abaqus/CFD solvers are executed together and both solvers exchange information at each co-simulation target time [29]. For the simulation, the thermal properties were considered constant (

Table 1. Physical and thermal properties of the materials used in the coupled FEM-CFD co-simulation.

Material Properties	Copper (FEM Model)	Water (CFD Model)
Density (kg/m3)	8930	997.9
Thermal conductivity (W/m °C)	384	0.598
Specific heat capacity (J/kg °C)	386	4183
Emissivity	0.92 1	-
Heat loss coefficient (W/m2 °C)	4.6 1	-
Viscosity (N/m2 s)	-	0.001

¹ Copper tube coated with non-selective black paint.

).

2.6.1. FEM Model

For the FEM model of the absorber, a transient heat transfer analysis in Abaqus/Standard was employed, in which the temperature field was calculated without considering stress or deformation [29]. The mesh comprised a total of 6400 8-node linear heat transfer brick elements (DC3D8) for the absorber without fins, as shown in Figure 6a,b. A mesh sensitivity analysis showed that this mesh size was deemed sufficient for convergence. The cylindrical surface of the absorber without fins was divided into 80 sections to match those in the MATLAB software (Section 2.5). The thermal loading on the absorber surface was input as surface heat flux (W/m²) on each of the 80 sections (Figure 6b) using the data obtained in MATLAB. A similar procedure was employed for the absorbers with segmented fins and continuous fins. Although the difference between the absorber and ambient temperatures was less than 20 °C and the maximum absorber temperature was less than 50 °C, heat loss due to convection and ambient blackbody radiation was taken into account in the simulation by using the heat loss coefficient and emissivity values shown in Table 1, respectively, because the absorber was coated with nonselective black paint [31,32]. The initial temperature of the absorber for the simulation validation was based on the experimental measurements. The material properties used for the copper tube absorber in the FEM model are shown in Table 1 [33].

2.6.2. CFD Model

For the CFD model of the fluid (water), a transient flow analysis was employed in Abaqus/CFD. The solver is based on Navier-Stokes equations for incompressible fluids and utilizes the Spalart-Allmaras turbulence model [29]. The mesh comprised 19,200 8-node linear fluid brick elements (FC3D8) as shown in Figure 6a,c. A mesh sensitivity analysis showed that this mesh size was deemed sufficient for convergence. The boundary conditions of the fluid were defined as follows: a normal inlet velocity of 0.0076 m/s (based on the experimental measurement of 0.36 L/min) and an outlet pressure of 0 MPa (Figure 6c). A no-slip/no-penetration wall boundary condition was applied to the surface of the fluid (Figure 6c). The material properties used for the water in the CFD model are shown in Table 1 [34].

2.6.3. CPC Absorber Models

Figure 7 shows the mesh of the three different types of absorbers that were modeled, that is, CPC absorber without fins (Figure 7a), CPC absorber with segmented fins (Figure 7b) and CPC absorber with continuous fins (Figure 7c). While the CPC absorbers without and with segmented fins were validated experimentally, the CPC absorber with continuous fins was only assessed numerically.

3. Results and Discussion

3.1. Experimental Results

Figure 8 shows the inlet temperature T_i, outlet temperature T_o and absorber temperature T_a, as well as ambient temperature T_amb and global solar radiation measured experimentally from 6 a.m. to 6 p.m. on 1 March 2020 for both a CPC absorber without fins (Figure 8a) and a CPC absorber with segmented fins (Figure 8b). It can be seen that the increase in the outlet temperature is due to the increase in the global radiation. It can also be seen that the CPC collector with a finned absorber produces a larger temperature difference, ΔT = T_o − T_i, as a result of the increase in the available energy (power) on the absorber surface.

Figure 9 shows ΔT and the thermal efficiency ${\eta }_t$ for the absorbers without and with segmented fins. The efficiency ${\eta }_t$ was obtained using the following equation:

$${\eta }_t=\frac{\dot{m}{C}_p\mathsf{\Delta }T}{A_{a}I}$$

(1)

where $\dot{m}$ is the mass flow rate, $C_p$ is the specific heat capacity, A_a is the aperture area of the CPC collector and I is the global solar radiation. As previously mentioned, it can be seen in Figure 9 that ΔT is larger for the CPC with the absorber with segmented fins, which results in an increase in the efficiency of the CPC collector. The average ${\eta }_t$ of the CPC absorbers without fins and with segmented fins on 1 March 2020 was 42% and 57%, respectively, under the given experimental conditions. The average ${\eta }_t$ of the CPC absorber without fins is similar to the ${\eta }_t$ obtained using the same CPC system with a fixed tilt angle of 21° on an early winter day (~43%) [16].

The thermal efficiency ${\eta }_t$ can also be defined as:

$${\eta }_t=\frac{Q_u}{A_{a}I}$$

(2)

where $Q_u$ is the useful heat of the collector, which is defined as

$$Q_u=F_R{A}_a[I\left(\tau \alpha \right)-U_L\left(T_i-T_{amb}\right)]$$

(3)

where $F_R$ is the heat removal factor, $\left(\tau \alpha \right)$ is the transmittance-absorptance product and $U_L$ is the heat loss coefficient. Equation (3) is known as the Hottel-Whillier-Bliss equation. By substituting Equation (3) into Equation (2), ${\eta }_t$ can be expressed as

$${\eta }_t=F_R\left(\tau \alpha \right)-F_R{U}_L\left(\frac{T_i-T_{amb}}{I}\right)$$

(4)

Figure 10 shows the experimental ${\eta }_t$ versus $\left(T_i-T_{amb}\right)/L$ for the CPC collectors on 1 March 2020. Equation (4) was fitted to the experimental data as shown in Figure 10. The intercept $F_R\left(\tau \alpha \right)$ of the fitted curve with the ordinate axis for the CPC with segmented fins (0.584) is larger than that of the curve for the CPC without fins (0.405); the ratio of the two values is 1.45. This indicates that $F_R$ for the CPC with segmented fins is 45% larger than that of the CPC without fins (considering that $\left(\tau \alpha \right)$ is constant), which in turn indicates that the heat transfer from the absorber tube to the fluid is greater for the CPC with segmented fins when compared to the CPC without fins. On the other hand, the slope $F_R{U}_L$ of the curve for the CPC with segmented fins is 11.065 W$/$°C m², while for the CPC without fins it is 6.881 W$/$°C m². The ratio of these two values is 1.61, which indicates that the $U_L$ is larger for the CPC with segmented fins when compared to the CPC without fins. As a result of this analysis, the CPC collector with an absorber with segmented fins is more efficient than the CPC without fins; however, for large values of $\left(T_i-T_{amb}\right)/L$ (≥0.04), the difference between the values of the efficiency of the CPCs with and without segmented fins is less than ~10% (Figure 10).

3.2. Numerical Results

3.2.1. Model Validation and CPC Thermal Performance

Figure 11a shows a comparison of the predicted outlet temperature (using the coupled FEM-CFD simulation) and the experimentally measured outlet temperature T_o for both CPC collectors (absorber without fins and with segmented fins) from 6 a.m. to 6 p.m. on 1 March 2020. The predicted T_o is in agreement with the measured T_o with a difference of less than 0.5 °C. It is noted that the predicted curves in Figure 11a were obtained with inlet velocities of 0.0075 and 0.007 m/s for the absorber without fins and with segmented fins, respectively. This difference could be attributed to small variations in the mass flow rate between each CPC system evaluated experimentally; however, it is noted that the difference between the value of the inlet velocities used in the simulation and the experimental value is less than 10%. Figure 11b shows the predicted T_o for both CPCs using either the mapped heat flux load on the absorber surface (as describe in Section 2.6.1) or a homogeneous heat flux load based on the total energy on the absorber surface. It can be seen in Figure 11b that for the case of the absorber without fins, the difference between the predicted T_o when using the mapped heat flux and the homogeneous flux is negligible; however, for the finned absorbers, there is a difference of up to 1 °C. This demonstrates the advantage of using the mapped heat flux on the surface of the absorber with fins to obtain more accurate predictions.

Figure 12 shows contour plots of the predicted temperatures of the absorbers using the FEM-CFD simulations at 12 p.m. (noon) on the 1 March 2020. Contour plots of the temperatures of the cross section at the outlet are also shown in Figure 12. It can be seen that the temperature increases from the inlet to the outlet in the direction of the flow, as expected, due to the transfer of heat from the absorber to the water. Cross sections show that the temperature of the water is higher in the zones closer to the absorber tube wall and colder in the center of tube. Figure 12 shows that higher temperatures were obtained with the finned absorbers due to the additional energy received on the absorber surface (see Section 3.2.2) that is consequently transferred to the water.

3.2.2. Effect of Fins on Thermal Performance at Different Seasons of the Year

Figure 13a shows the predicted temperature difference ΔT when using the FEM-CFD simulations from 6 a.m. to 6 p.m. on 1 March 2020 (late winter) with a constant inlet temperature T_i of 27 °C (corresponding to the initial T_i measured experimentally on that day) and a constant inlet velocity of 0.0076 m/s (0.36 L/min) for the different CPC collectors. Figure 13a also shows the power (energy per unit time) on the absorber surface obtained with the ray tracing simulations. Figure 13b shows an image of the incident angle of the solar rays impacting the CPC collector on the same day at noon (12 p.m.), for illustration purposes. It can be seen that the highest available power is obtained with the CPC absorber with continuous fins, while the lowest power available is obtained with the CPC absorber without fins. This results in an increase in ΔT with the increase in the surface area of the absorber due to the fins. Figure 13c,d show the results for early winter (15 January 2021) with a constant inlet temperature T_i of 23 °C (corresponding to the initial T_i measured experimentally on that day) and a constant inlet velocity of 0.0076 m/s (0.36 L/min) for the different CPC collectors. It can be seen that a similar ΔT is obtained for both days (early and late winter) when similar CPCs are compared with each other because the average power (from 8 a.m. to 5 p.m.) on the absorber surfaces is similar on both days (

Table 2. Average power (from 8 a.m. to 5 p.m.) on the surfaces of the different absorbers on late winter, early winter and summer.

CPC Absorber	Average Power P (W) 1 March 2020 (Late Winter)	Average Power P (W) 15 January 2021 (Early Winter)	Average Power P (W) 9 July 2020 (Summer)
Without fins	61.4	59.2	62.2
With segmented fins	69.9	69.5	62.8
With continuous fins	76.2	78.5	63.3

). Figure 13e,f show the results for summer (9 July 2020) with a constant inlet temperature T_i of 34 °C (corresponding to the initial T_i measured experimentally on that day) and a constant inlet velocity of 0.0076 m/s (0.36 L/min) for the different CPC collectors. It can be seen that for summer (Figure 13e), the average power on the surfaces of the different absorbers is similar (Table 2) due to the incident angle of the solar rays impacting them (Figure 13f), which results in a similar increase in ΔT. It is noted that the average power on the finned absorbers of the non-tracking CPC is lower in summer when compared to winter (Table 2).

Figure 14 shows both the transverse and the longitudinal incidence angle modifier (IAM) for the different CPC absorbers, which was calculated using the ray tracing simulations and the following equation [35]:

$$IAM\left(\theta \right)=\frac{{\eta }_o\left(\theta \right)}{{\eta }_o\left(0°\right)}$$

(5)

where ${\eta }_o\left(\theta \right)$ is the optical efficiency as a function of the incidence angle $\theta$ and ${\eta }_o\left(0°\right)$ is the optical efficiency when $\theta$ = $0°$. ${\eta }_o\left(\theta \right)$ was estimated using the maximum value given by the following equation [36]:

$${\eta }_o\left(\theta \right)=\frac{P_c\left(\theta \right)}{A_{a}I}$$

(6)

where $P_c\left(\theta \right)$ is the power on the absorber as a function of the incidence angle $\theta$. When the longitudinal IAM is calculated, $\theta ={\theta }_l$, where ${\theta }_l$ is the angle between the CPC collector normal vector and the sun position vector projected in a plane parallel with the trough axis of the collector (while keeping the CPC aperture area normal to the sun rays). When the transverse IAM is calculated, $\theta ={\theta }_t$, where ${\theta }_t$ is the angle between the CPC collector normal vector and the sun position vector projected in a plane perpendicular to the trough axis of the collector (while ${\theta }_l=0$) [35]. It can be seen in Figure 14 that the longitudinal IAM is similar for all CPC absorbers for all angles $\theta$. It can also be seen that the transverse IAM decreases for all CPC absorbers when $\theta$ increases from 0° to 10°, and then increases when $\theta$ increases from 10° to 30° for the absorber without fins and when $\theta$ increases from 10° to 20° for the absorbers with segmented fins and with continuous fins. This increase in IAM could be related to the combination between direct light and the reflected light from the top section of the reflective surface [37]. Subsequently, the transverse IAM decreases with a further increase in $\theta$ for all CPC absorbers. It can also be seen that the transverse IAM drops rapidly for $\theta$ > 45°, which is related to the half-angle of acceptance of 45° of the CPCs, as observed for another CPC collector with the same half-angle of acceptance [38]. Transversal IAM has a value of zero for $\theta$ ≥ 60° for all CPC absorbers.

3.2.3. Effect of Mass Flow Rate

Figure 15a,b show the predicted maximum temperature difference ΔT versus the mass flow rate $\dot{m}$ and the predicted thermal efficiency ${\eta }_t$ versus $\dot{m}$, respectively, for the different CPC collectors on 1 March 2020 with a constant inlet temperature of 27 °C. It is noted that the experimental mass flow rate was ~0.005 kg/s (0.36 L/min). It can be seen in Figure 15a that all CPCs exhibit a similar behavior, that is, there is an increase in the maximum ΔT with a decrease in the $\dot{m}$ as expected because lower $\dot{m}$ allows higher heat transfer from the absorber to the water; however, a lower $\dot{m}$ could result in less hot water availability. The largest ΔT was observed for the CPC with an absorber with continuous fins for all mass flow rates. Figure 15b shows that for all CPCs, there is a sharp increase in the thermal efficiency ${\eta }_t$ with an increase in the $\dot{m}$ from 0.001 to 0.002 kg/s. For the CPC with continuous fins, there is a slight increase in ${\eta }_t$ when $\dot{m}$ increases from 0.002 to 0.005 kg/s, and a decrease in ${\eta }_t$ from 0.005 to 0.01 kg/s. For the CPC with segmented fins, ${\eta }_t$ remains almost the same from 0.002 to 0.005 kg/s and decreases from 0.005 to 0.01 kg/s. For the CPC without fins, ${\eta }_t$ decreases from 0.002 to 0.006 kg/s and keeps decreasing at a larger rate from 0.006 to 0.01 kg/s; however, the difference between the values of ${\eta }_t$ at 0.002 and 0.006 is ~1%. The effect of the $\dot{m}$ on the ${\eta }_t$ has been previously observed [39] and it is attributed to the rate of heat transfer. The initial increase in ${\eta }_t$ with the increase in $\dot{m}$ is attributed to the higher water velocity, which, in turn, increases the rate of heat transfer to the water [40]; however, after an optimal value of $\dot{m}$ is reached, the ${\eta }_t$ decreases with further increase in the $\dot{m}$.

3.3. Discussion

The results presented here have shown that the design and fabrication of a small-size, low-cost and low-maintenance CPC collector is feasible, which could be used for residential applications, and at the same time promote a lower environmental footprint and sustainability by using solar energy for water heating. Among the technical advantages of the proposed CPCs are their small size and low weight. The area and weight of the proposed CPCs is 0.22 m² and ~5 kg, respectively. This is in contrast with the area and weight of 1.1 m² and 30 kg, respectively, for the flat plate collector previously developed by the authors [41] or with the area and weight of 1.6 m² and ~30 kg, respectively, for a commercial evacuated tube collector [42]. The small size and low weight of the proposed CPCs give them an advantage to be used in low income and remote areas, where the rooftops of some houses are small and are made of nonstructural materials. Another advantage of the proposed CPCs is the low maintenance and its associated costs because the materials for the fabrication of the CPCs are locally available and the repairs are not complicated [15]. An economic advantage of the proposed CPCs is the low fabrication cost, which can be seen in

Table 3. Estimated fabrication cost for the proposed CPC collectors and flat plate collector (all costs are in USD).

	CPC Collector without Fins	CPC Collector with Segmented Fins	Flat Plate Collector	Evacuated Tube Collector
Copper tube, fins, fittings	$23	$47	$65	-
Steel sheet and supports	$11	$11	$15	-
Aluminum sheet	$20	$20	-	-
Aluminum frame	-	-	$15	-
Thermal insulation	$6	$6	$10	-
Glass cover	$5	$5	$20	-
Total cost	$65	$89	$125	$300 1

¹ Retail price.

, in which the estimated fabrication cost of the CPCs with an absorber without fins and with segmented fins as well as a flat plate collector are presented. Moreover, the retail price of a commercial evacuated tube collector is presented for illustration purposes. It can be seen that the fabrication cost of the proposed CPCs is lower than the other options. The cost of the CPC with an absorber with segmented fins is 40% higher than that of the CPC with an absorber without fins; however, the measured average efficiency of the CPC with segmented fins is 37% higher than that of the CPC without fins on a late winter day, when the need for hot water increases. It is acknowledged that a comprehensive techno-economic analysis of the proposed CPCs should be performed to carry out a fair comparison with other CPC systems available and for the assessment of the incorporation of fins to the absorber due to the high price of copper.

It is also acknowledged that further studies should be performed to optimize the performance of the CPC in the wintertime, when the water is cooler, to reach a larger temperature difference between the inlet and outlet temperatures. These studies should include numerical simulations and experimental work to obtain the optimum mass flow rate, using a pump to achieve higher temperatures, without limiting the availability of hot water. The thermosiphon effect should also be investigated [41]. Further work should also include the assessment of geometrical parameters, such as fin position and size, and absorber diameter and length, and their optimization.

The numerical methodology—which included the mapping of the solar power (energy), obtained via ray-tracing analysis, on the absorber surface of the FEM model and a coupled thermal FEM-CFD analysis to estimate the temperature of the water—was capable of describing the thermal performance of the CPCs with and without fins, and it could be used to predict the thermal performance of other CPCs with different geometries and configurations in order to obtain optimized designs prior to manufacturing and experimental testing. The numerical results showed that the mapping of the heat flux on the CPC absorber surface with fins should be used to obtain more accurate predictions when compared to an analysis using homogenous heat flux on the surface of the absorber. Our results warrant further research to determine an optimum design of small-size, low-temperature CPCs for residential applications that is low cost and requires minimum maintenance.

4. Conclusions

In this work, the thermal performance of a small size CPC collector with an absorber with and without fins was assessed experimentally and by using a numerical methodology in Merida, Mexico (21.02° N, 89.63° W). The following conclusions can be drawn from this study:

• Using a small-size, low-temperature CPC collector with an aperture area of ~0.18 m² for water heating in residential applications is feasible; however, the design of the CPC should be optimized to obtain higher temperatures.
• The proposed numerical methodology, which included ray tracing simulations to map the heat flux on the absorber surface of the FEM model, which was coupled with a CFD model to estimate the temperature of the water, was capable of describing the thermal performance of the CPC collector.
• Mass flow rate is an important parameter that should be determined and optimized to obtain the maximum temperature difference between inlet and outlet temperatures and the optimal thermal efficiency while at the same time providing enough hot water.
• The best thermal performance of the CPC collectors in winter was observed when absorbers with fins were used, due to the increase in surface area.
• The use of copper fins in the absorber could also result in an increase in the cost of the fabrication of the CPC collector. Therefore, a comprehensive techno-economic analysis is needed to complement the thermal performance study.