Reconstructing the Free Energy Profiles Describing the Switching Mechanism of a pH-Dependent DNA Nanodevice from ABMD Simulations
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. DNA Nanoswitch Modelling
- DIPRO5: AAGAAAAGAATTTTATTCTTTTCTTCTTTGTTCTTTTCTT
- DIPRO15: AAGAAAAGAATTTTATTCTTTTCTTCTTTGGTTTGGTTTGTTCTTTTCTT
- DIPRO25: AAGAAAAGAATTTTATTCTTTTCTTCTTTGGTTTGGTTTGGTTTGGTTTGTTCTTTTCTT
- TETRA5: GAAGAAGGAATTTTACTTCTTCCTTCTTTGCTTCTTCCTT
- TETRA15: GAAGAAGGAATTTTACTTCTTCCTTCTTTGGTTTGGTTTGCTTCTTCCTT
- TETRA25: GAAGAAGGAATTTTACTTCTTCCTTCTTTGGTTTGGTTTGGTTTGGTTTGCTTCTTCCTT
2.2. MD and ABMD Simulations
2.3. Trajectory Analyses
3. Results
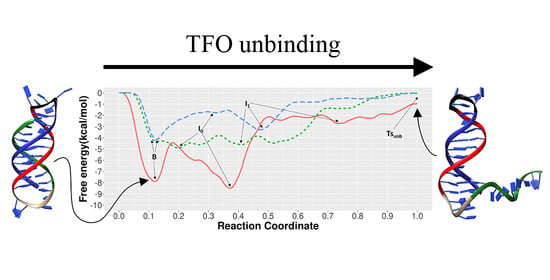
3.1. Unbinding of the TFO from the Double Helix
3.2. Conformational Variability of the Linker and Stability of the Double Helix
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chidchob, P.; Sleiman, H.F. Recent advances in DNA nanotechnology. Curr. Opin. Chem. Biol. 2018, 46, 63–70. [Google Scholar] [CrossRef] [PubMed]
- DeLuca, M.; Shi, Z.; Castro, C.E.; Arya, G. Dynamic DNA nanotechnology: Toward functional nanoscale devices. Nanoscale Horiz. 2020, 5, 182–201. [Google Scholar] [CrossRef]
- Keller, A.; Linko, V. Challenges and Perspectives of DNA Nanostructures in Biomedicine. Angew. Chem. Int. Ed. Engl. 2020. [Google Scholar] [CrossRef] [Green Version]
- Andersen, F.F.; Knudsen, B.; Oliveira, C.L.P.; Frøhlich, R.F.; Krüger, D.; Bungert, J.; Agbandje-McKenna, M.; Mckenna, R.; Juul, S.; Veigaard, C.; et al. Assembly and structural analysis of a covalently closed nano-scale DNA cage. Nucleic Acids Res. 2008, 36, 1113–1119. [Google Scholar] [CrossRef]
- Bhatia, D.; Mehtab, S.; Krishnan, R.; Indi, S.S.; Basu, A.; Krishnan, Y. Icosahedral DNA nanocapsules by modular assembly. Angew. Chem. Int. Ed. 2009, 48, 4134–4137. [Google Scholar] [CrossRef]
- Alves, C.; Iacovelli, F.; Falconi, M.; Cardamone, F.; Morozzo della Rocca, B.; de Oliveira, C.L.P.; Desideri, A. A Simple and Fast Semiautomatic Procedure for the Atomistic Modeling of Complex DNA Polyhedra. J. Chem. Inf. Model. 2016, 56, 941–949. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, J.; Cebulla, M.P.J.; Mönninghoff, S.; von Kiedrowski, G. Self-Assembly of a DNA Dodecahedron from 20 Trisoligonucleotides withC3h Linkers. Angew. Chem. Int. Ed. 2008, 47, 3626–3630. [Google Scholar] [CrossRef]
- Fan, S.; Wang, D.; Kenaan, A.; Cheng, J.; Cui, D.; Song, J. Create Nanoscale Patterns with DNA Origami. Small 2019, 15, 1805554. [Google Scholar] [CrossRef] [PubMed]
- Endo, M.; Sugiyama, H. DNA Origami Nanomachines. Molecules 2018, 23, 1766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andersen, E.S.; Dong, M.; Nielsen, M.M.; Jahn, K.; Subramani, R.; Mamdouh, W.; Golas, M.M.; Sander, B.; Stark, H.; Oliveira, C.L.P.; et al. Self-assembly of a nanoscale DNA box with a controllable lid. Nature 2009, 459, 73–76. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, D.N.; Kilchherr, F.; Dietz, H.; Bathe, M. Quantitative prediction of 3D solution shape and flexibility of nucleic acid nanostructures. Nucleic Acids Res. 2012, 40, 2862–2868. [Google Scholar] [CrossRef] [PubMed]
- Grossi, G.; Dalgaard Ebbesen Jepsen, M.; Kjems, J.; Andersen, E.S. Control of enzyme reactions by a reconfigurable DNA nanovault. Nat. Commun. 2017, 8, 992. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Madhanagopal, B.R.; Zhang, S.; Demirel, E.; Wady, H.; Chandrasekaran, A.R. DNA Nanocarriers: Programmed to Deliver. Trends Biochem. Sci. 2018, 43, 997–1013. [Google Scholar] [CrossRef]
- Juul, S.; Iacovelli, F.; Falconi, M.; Kragh, S.L.; Christensen, B.; Frøhlich, R.; Franch, O.; Kristoffersen, E.L.; Stougaard, M.; Leong, K.W.; et al. Temperature-Controlled Encapsulation and Release of an Active Enzyme in the Cavity of a Self-Assembled DNA Nanocage. ACS Nano 2013, 7, 9724–9734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Franch, O.; Iacovelli, F.; Falconi, M.; Juul, S.; Ottaviani, A.; Benvenuti, C.; Biocca, S.; Ho, Y.-P.; Knudsen, B.R.; Desideri, A. DNA hairpins promote temperature controlled cargo encapsulation in a truncated octahedral nanocage structure family. Nanoscale 2016, 8, 13333–13341. [Google Scholar] [CrossRef] [PubMed]
- Raniolo, S.; Iacovelli, F.; Unida, V.; Desideri, A.; Biocca, S. In Silico and In Cell Analysis of Openable DNA Nanocages for miRNA Silencing. Int. J. Mol. Sci. 2019, 21, 61. [Google Scholar] [CrossRef] [Green Version]
- Chandrasekaran, A.R.; Wady, H.; Subramanian, H.K.K. Nucleic Acid Nanostructures for Chemical and Biological Sensing. Small 2016, 12, 2689–2700. [Google Scholar] [CrossRef]
- Rutten, I.; Daems, D.; Lammertyn, J. Boosting biomolecular interactions through DNA origami nano-tailored biosensing interfaces. J. Mater. Chem. B 2020. [Google Scholar] [CrossRef]
- Mathur, D.; Medintz, I.L. The Growing Development of DNA Nanostructures for Potential Healthcare-Related Applications. Adv. Healthc. Mater. 2019, 8, 1801546. [Google Scholar] [CrossRef] [Green Version]
- Yatsunyk, L.A.; Mendoza, O.; Mergny, J.L. Nano-oddities: Unusual nucleic acid assemblies for DNA-based nanostructures and nanodevices. Acc. Chem. Res. 2014, 47, 1836–1844. [Google Scholar] [CrossRef]
- Hu, Y.; Cecconello, A.; Idili, A.; Ricci, F.; Willner, I. Triplex DNA Nanostructures: From Basic Properties to Applications. Angew. Chem. Int. Ed. 2017, 56, 15210–15233. [Google Scholar] [CrossRef] [PubMed]
- Porchetta, A.; Idili, A.; Vallée-Bélisle, A.; Ricci, F. General Strategy to Introduce pH-Induced Allostery in DNA-Based Receptors to Achieve Controlled Release of Ligands. Nano Lett. 2015, 15, 4467–4471. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuzyk, A.; Urban, M.J.; Idili, A.; Ricci, F.; Liu, N. Selective control of reconfigurable chiral plasmonic metamolecules. Sci. Adv. 2017, 3, e1602803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ijäs, H.; Hakaste, I.; Shen, B.; Kostiainen, M.A.; Linko, V. Reconfigurable DNA Origami Nanocapsule for pH-Controlled Encapsulation and Display of Cargo. ACS Nano 2019, 13, 5959–5967. [Google Scholar] [CrossRef] [Green Version]
- Farag, N.; Mattossovich, R.; Merlo, R.; Nierzwicki, Ł.; Palermo, G.; Porchetta, A.; Perugino, G.; Ricci, F. Folding-upon-Repair DNA Nanoswitches for Monitoring the Activity of DNA Repair Enzymes. Angew. Chem. Int. Ed. 2021, 60, 7283–7289. [Google Scholar] [CrossRef] [PubMed]
- Iacovelli, F.; Idili, A.; Benincasa, A.; Mariottini, D.; Ottaviani, A.; Falconi, M.; Ricci, F.; Desideri, A. Simulative and Experimental Characterization of a pH-Dependent Clamp-like DNA Triple-Helix Nanoswitch. J. Am. Chem. Soc. 2017, 139, 5321–5329. [Google Scholar] [CrossRef] [Green Version]
- Iacovelli, F.; Cabungcal Hernandez, K.; Desideri, A.; Falconi, M. Probing the Functional Topology of a pH-Dependent Triple Helix DNA Nanoswitch Family through Gaussian Accelerated MD Simulation. J. Chem. Inf. Model. 2019, 59, 2746–2752. [Google Scholar] [CrossRef] [PubMed]
- Ottaviani, A.; Iacovelli, F.; Idili, A.; Falconi, M.; Ricci, F.; Desideri, A. Engineering a responsive DNA triple helix into an octahedral DNA nanostructure for a reversible opening/closing switching mechanism: A computational and experimental integrated study. Nucleic Acids Res. 2018, 46, 9951–9959. [Google Scholar] [CrossRef]
- Mariottini, D.; Idili, A.; Nijenhuis, M.A.D.; Ercolani, G.; Ricci, F. Entropy-Based Rational Modulation of the p K a of a Synthetic pH-Dependent Nanoswitch. J. Am. Chem. Soc. 2019, 141, 11367–11371. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A Visualization System for Exploratory Research and Analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.-J.; Olson, W.K. 3DNA: A versatile, integrated software system for the analysis, rebuilding and visualization of three-dimensional nucleic-acid structures. Nat. Protoc. 2008, 3, 1213–1227. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Ivani, I.; Dans, P.D.; Noy, A.; Pérez, A.; Faustino, I.; Hospital, A.; Walther, J.; Andrio, P.; Goñi, R.; Balaceanu, A.; et al. Parmbsc1: A refined force field for DNA simulations. Nat. Methods 2015, 13, 55–58. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Goga, N.; Rzepiela, A.J.; De Vries, A.H.; Marrink, S.J.; Berendsen, H.J.C. Efficient algorithms for langevin and DPD dynamics. J. Chem. Theory Comput. 2012, 8, 3637–3649. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aoki, K.M.; Yoneya, M.; Yokoyama, H. Constant Pressure Md Simulation Method. Mol. Cryst. Liq. Cryst. 2004, 413, 109–116. [Google Scholar] [CrossRef]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of nalkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef] [Green Version]
- Miyamoto, S.; Kollman, P.A. SETTLE: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Babin, V.; Roland, C.; Sagui, C. Adaptively biased molecular dynamics for free energy calculations. J. Chem. Phys. 2008, 128, 134101. [Google Scholar] [CrossRef] [Green Version]
- Barducci, A.; Bussi, G.; Parrinello, M. Well-tempered metadynamics: A smoothly converging and tunable free-energy method. Phys. Rev. Lett. 2008, 100, 020603. [Google Scholar] [CrossRef] [Green Version]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Daura, X.; Gademann, K.; Jaun, B.; Seebach, D.; van Gunsteren, W.F.; Mark, A.E. Peptide Folding: When Simulation Meets Experiment. Angew. Chem. Int. Ed. 1999, 38, 236–240. [Google Scholar] [CrossRef]
- Blanchet, C.; Pasi, M.; Zakrzewska, K.; Lavery, R. CURVES+ web server for analyzing and visualizing the helical, backbone and groove parameters of nucleic acid structures. Nucleic Acids Res. 2011, 39, W68–W73. [Google Scholar] [CrossRef] [Green Version]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Ginestet, C. Ggplot2: Elegant Graphics for Data Analysis. J. R. Stat. Soc. Ser. A (Stat. Soc.) 2011, 174, 245–246. [Google Scholar] [CrossRef]
- Iannone, F.; Ambrosino, F.; Bracco, G.; De Rosa, M.; Funel, A.; Guarnieri, G.; Migliori, S.; Palombi, F.; Ponti, G.; Santomauro, G.; et al. CRESCO ENEA HPC clusters: A working example of a multifabric GPFS Spectrum Scale layout. In Proceedings of the 2019 International Conference on High Performance Computing & Simulation (HPCS), Dublin, Ireland, 15–19 July 2019; pp. 1051–1052. [Google Scholar]
- Zuker, M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003, 31, 3406–3415. [Google Scholar] [CrossRef]
- Zadeh, J.N.; Steenberg, C.D.; Bois, J.S.; Wolfe, B.R.; Pierce, M.B.; Khan, A.R.; Dirks, R.M.; Pierce, N.A. NUPACK: Analysis and design of nucleic acid systems. J. Comput. Chem. 2011, 32, 170–173. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romeo, A.; Falconi, M.; Desideri, A.; Iacovelli, F. Reconstructing the Free Energy Profiles Describing the Switching Mechanism of a pH-Dependent DNA Nanodevice from ABMD Simulations. Appl. Sci. 2021, 11, 4052. https://doi.org/10.3390/app11094052
Romeo A, Falconi M, Desideri A, Iacovelli F. Reconstructing the Free Energy Profiles Describing the Switching Mechanism of a pH-Dependent DNA Nanodevice from ABMD Simulations. Applied Sciences. 2021; 11(9):4052. https://doi.org/10.3390/app11094052
Chicago/Turabian StyleRomeo, Alice, Mattia Falconi, Alessandro Desideri, and Federico Iacovelli. 2021. "Reconstructing the Free Energy Profiles Describing the Switching Mechanism of a pH-Dependent DNA Nanodevice from ABMD Simulations" Applied Sciences 11, no. 9: 4052. https://doi.org/10.3390/app11094052
APA StyleRomeo, A., Falconi, M., Desideri, A., & Iacovelli, F. (2021). Reconstructing the Free Energy Profiles Describing the Switching Mechanism of a pH-Dependent DNA Nanodevice from ABMD Simulations. Applied Sciences, 11(9), 4052. https://doi.org/10.3390/app11094052