NHL and RCGA Based Multi-Relational Fuzzy Cognitive Map Modeling for Complex Systems
Abstract
:1. Introduction
2. Backgrounds
2.1. Fuzzy Cognitive Map (FCM)
- C = {C1,C2,…,CN} is a set of N concepts forming the nodes of a graph.
- W: (Ci,Cj)→wij is a function associating wij with a pair of concepts, with wij equal to the weight of edge directed from Ci to Cj, where wijϵ[−1, 1]. Thus, W(NN) is a connection matrix.

- A: Ci → Ai(t) is a function that associates each concept Ci with the sequence of its activation degrees such as for tϵT, Ai(t)ϵL given its activation degree at the moment t. A(0)ϵLT indicates the initial vector and specifies initial values of all concept nodes and A(t)ϵLT is a state vector at certain iteration t.
- f is a transformation or activation function, which includes recurring relationship on t ≥ 0 between A(t + 1) and A(t).
- Bivalent
- Trivalent
- Logistic
2.2. FCM Learning Algorithms
2.2.1. Nonlinear Hebbian Learning (NHL)
2.2.2. Real-Coded Genetic Algorithm (RCGA)
2.3. Problem Statements
3. Materials and Methods
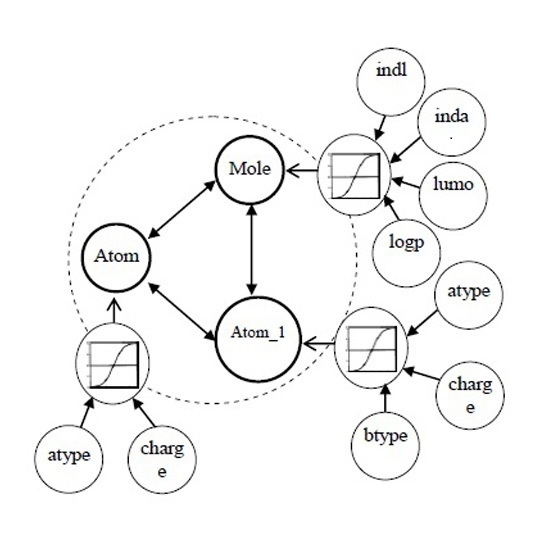
3.1. Multi-Relational FCM
- Cn2: {{C1i}…,{Cji},…{Cni}} is a set of concepts, {Cji} is on behalf of a coarse-grained concept in j dimension, and Cji is ith fine-grained concept in bottom-level of jth dimension.
- Wn2: {{Wj}, {Wij}}. <{Cji}> → Wj is a function associating Wj among jth dimension, Wj:{wij}; (<{C1i}>…, <{Cji}>,…<{Cni}>) → {Wij} is function associating between coarse-grained concepts.
- An2: Cji → Aji(t), {Cji} → Aj(t). Aj(t) is a function f at iteration t.
- f is a transformation function, which includes recurring relationship on t ≥ 0 among Aj(t + 1), Aji(t) and Ai(t), where Aj(0) is referred out based on the weight vector Wj, got by multi-instances oriented NHL, in low-level FCM.
3.2. Multi-Instances Oriented NHL

- Step 1:
- Random initialize the weight vector wj(t), t = 0, p = 0 and input all instance {Aji}
- Step 2:
- Calculate the mathematical expectation of Aj2 of all {Aji}
- Step 3:
- Set t = t + 1, repeat for each iteration step t:
- 3.1
- Set p = p + 1, to the pth instance:
- 3.1.1
- Adjust wj(t) matrix to {Aji}p by Equation (9)
- 3.2
- Calculate the Aj2 to all {Aji} by Equation (10)
- 3.3
- Determine whether Aj2 is maximum or not at present
- 3.4
- If Aj2 is maximum, output the optimal wj(t)
- Step 4:
- Return the final weight vector wj(t)
3.3. NHL and RCGA Based Integrated Algorithm
| Parameters | Values | Meanings |
|---|---|---|
| probability of recombination | 0.9 | probability of single-point crossover |
| probability of mutation | 0.5 | probability of random mutation |
| population_size | 50 | the number of chromosomes |
| max_generation | 500,000 | a maximum number of generations |
| max_fitness | [0.6, 0.9] | fitness thresholds |
| a | 1000 | a parameter in Equation (13) |
- Step 1:
- Initialize the parameters by the Table 1
- Step 2:
- Randomly initialize population_size chromosomes, g = 0, t = 0
- Step 3:
- Repeat for each dimension j:
- 3.1
- Calculate Aj(t) by Equation (11) and wj based on M_NHL
- Step 4:
- Repeat for each chromosome:
- 4.1
- Calculate the fitness by Aj(t) and Equation (13)
- Step 5:
- Get max of the fitness and the W
- Step 6:
- if max of fitness not more than max_fitness and g not more than max_generation
- 6.1
- Select chromosomes by roulette wheel selection
- 6.2
- Recombination the chromosomes by single-point crossover
- 6.3
- Random mutation to the chromosomes by the probability
- 6.4
- Set t = i + 1, Repeat for each chromosome:
- 6.4.1
- Calculate Aj(t) by Equation (1)
- 6.5
- Set g = g + 1, go to Step 5
- Step 7:
- The W is the optimal chromosome.
4. Results and Discussion



| Background | Description |
|---|---|
| BK0 | Each compound includes the attributes of bond types, atom types, and partial charges on atoms |
| BK1 | Each compound includes indl and inda of mole besides those in BK0 |
| BK2 | Each compound includes all attributes that are logp and lumo of mole besides those in BK1 |

| Backgrounds | Runtime(s) | Accuracy (%) |
|---|---|---|
| BK0 | 0.78 | 82.3% |
| BK1 | 0.8 | 82.9% |
| BK2 | 0.8 | 82.7% |

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Han, J.W.; Kamber, M. Concept and Technology of Data Mining; Machinery Industry Press: Beijing, China, 2007; pp. 373–383. [Google Scholar]
- Spyropoulou, E.; de Bie, T.; Boley, M. Interesting pattern mining in multi-relational data. Data Knowl. Eng. 2014, 28, 808–849. [Google Scholar] [CrossRef]
- Yin, X.; Han, J.; Yang, J.; Yu, P.S. Efficient classification across multiple database relations: A CrossMine approach. IEEE Trans. Knowl. Data Eng. 2006, 18, 770–783. [Google Scholar] [CrossRef]
- Xu, G.; Yang, B.; Qin, Y.; Zhang, W. Multi-relational Naive Bayesian classifier based on mutual information. J. Univ. Sci. Technol. Beijing 2008, 30, 943–966. [Google Scholar]
- Liu, H.; Yin, X.; Han, J. An efficient multi-relational naive Bayesian classifier based on semantic relationship graphs. In Proceedings of the 2005 ACM-SIGKDD Workshop on Multi-Relational Data Mining (KDD/MRDM05), Chicago, IL, USA, 21–24 August 2005.
- Kosko, B. Fuzzy cognitive maps. Int. J. Man Mach. Studs. 1986, 24, 65–75. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Salmeron, J.L. A review of fuzzy cognitive maps research during the last decade. IEEE Trans. Fuzzy Syst. 2013, 12, 66–79. [Google Scholar] [CrossRef]
- Groumpos, P.P. Large scale systems and fuzzy cognitive maps: A critical overview of challenges and research opportunities. Annu. Rev. Control 2014, 38, 93–102. [Google Scholar] [CrossRef]
- Zhang, Y. Modeling and Control of Dynamic Systems Based on Fuzzy Cognitive Maps. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2012. [Google Scholar]
- Mago, V.K.; Bakker, L.; Papageorgiou, E.I.; Alimadad, A.; Borwein, P.; Dabbaghian, V. Fuzzy cognitive maps and cellular automata: An evolutionary approach for social systems modeling. Appl. Soft Comput. 2012, 12, 3771–3784. [Google Scholar] [CrossRef]
- Subramanian, J.; Karmegam, A.; Papageorgiou, E.; Papandrianos, N.I.; Vasukie, A. An integrated breast cancer risk assessment and management model based on fuzzy cognitive maps. Comput. Methods Programs Biomed. 2015, 118, 280–297. [Google Scholar] [CrossRef] [PubMed]
- Szwed, P.; Skrzynski, P. A new lightweight method for security risk assessment based on fuzzy cognitive maps. Appl. Math. Comput. Sci. 2014, 24, 213–225. [Google Scholar] [CrossRef]
- Peng, Z.; Peng, J.; Zhao, W.; Chen, Z. Research on FCM and NHL based High Order mining driven by big data. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Papakostas, G.A.; Koulouriotis, D.E.; Polydoros, A.S.; Tourassis, V.D. Towards Hebbian learning of fuzzy cognitive maps in pattern classification problems. Expert Syst. Appl. 2012, 39, 10620–10629. [Google Scholar] [CrossRef]
- Salmeron, J.L.; Papageorgiou, E.I. Fuzzy grey cognitive maps and nonlinear Hebbian learning in process control. Appl. Intell. 2014, 41, 223–234. [Google Scholar] [CrossRef]
- Beena, P.; Ganguli, R. Structural damage detection using fuzzy cognitive maps and Hebbian learning. Appl. Soft Comput. 2011, 11, 1014–1020. [Google Scholar] [CrossRef]
- Kim, M.-C.; Kim, C.O.; Hong, S.R.; Kwon, I.-H. Forward-backward analysis of RFID-enabled supply chain using fuzzy cognitive map and genetic algorithm. Expert Syst. Appl. 2008, 35, 1166–1176. [Google Scholar] [CrossRef]
- Froelich, W.; Papageorgiou, E.I. Extended evolutionary learning of fuzzy cognitive maps for the prediction of multivariate time-series. Fuzzy Cogn. Maps Appl. Sci. Eng. 2014, 2014, 121–131. [Google Scholar]
- Froelich, W.; Salmeron, J.L. Evolutionary learning of fuzzy grey cognitive maps for forecasting of multivariate, interval-valued time series. Int. J. Approx. Reason. 2014, 55, 1319–1335. [Google Scholar] [CrossRef]
- Wojciech, S.; Lukasz, K.; Witold, P. A divide and conquer method for learning large fuzzy cognitive maps. Fuzzy Sets Syst. 2010, 161, 2515–2532. [Google Scholar]
- Sudjianto, A.; Hassoun, M.H. Statistical basis of nonlinear Hebbian learning and application to clustering. Neural Netw. 1995, 8, 707–715. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Wu, L.; Chen, Z. NHL and RCGA Based Multi-Relational Fuzzy Cognitive Map Modeling for Complex Systems. Appl. Sci. 2015, 5, 1399-1411. https://doi.org/10.3390/app5041399
Peng Z, Wu L, Chen Z. NHL and RCGA Based Multi-Relational Fuzzy Cognitive Map Modeling for Complex Systems. Applied Sciences. 2015; 5(4):1399-1411. https://doi.org/10.3390/app5041399
Chicago/Turabian StylePeng, Zhen, Lifeng Wu, and Zhenguo Chen. 2015. "NHL and RCGA Based Multi-Relational Fuzzy Cognitive Map Modeling for Complex Systems" Applied Sciences 5, no. 4: 1399-1411. https://doi.org/10.3390/app5041399
APA StylePeng, Z., Wu, L., & Chen, Z. (2015). NHL and RCGA Based Multi-Relational Fuzzy Cognitive Map Modeling for Complex Systems. Applied Sciences, 5(4), 1399-1411. https://doi.org/10.3390/app5041399