Correlation of Plastic Strain Energy and Acoustic Emission Energy in Reinforced Concrete Structures
Abstract
:1. Introduction
2. Cyclic Loading
2.1. RC Beams
2.2. Beam-Column Connection
3. Seismic Loading
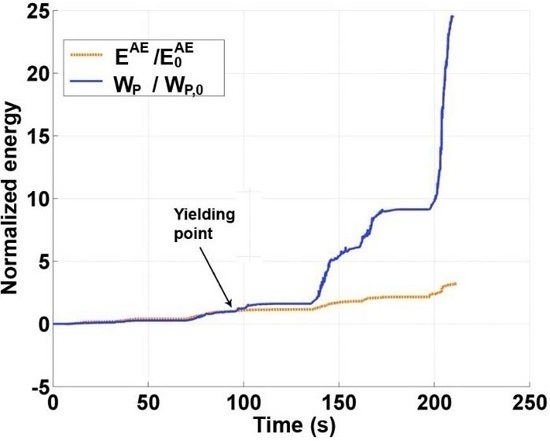
3.1. RC Slab
3.2. RC Frame
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AE | Acoustic Emission |
| RC | Reinforced Concrete |
References
- Grosse, C.U.; Ohtsu, M. Acoustic Emission Testing; Springer: Berlin, Germany, 2008. [Google Scholar]
- Miller, R.K.; Hill, E.K.; Moore, P.O. Acoustic emission testing, NDT Handbook, 3rd ed.; American Society for Nondestructive Testing: Columbus, OH, USA, 2005. [Google Scholar]
- Ono, K. Application of acoustic emission for structure diagnosis. Diagnostyka 2011, 2, 3–18. [Google Scholar]
- Ohtsu, M. The history and development of acoustic emission in concrete engineering. Mag. Concr. Res. 1996, 48, 321–330. [Google Scholar] [CrossRef]
- ElBatanouny, M.; Larosche, A.; Mazzoleni, P.; Ziehl, P.; Matta, F.; Zappa, E. Identification of cracking mechanisms in scaled FRP reinforced concrete beams using acoustic emission. Exp. Mech. 2014, 54, 69–82. [Google Scholar] [CrossRef]
- Calabrese, L.; Campanella, G.; Proverbio, E. Identification of corrosion mechanisms by univariate and multivariate statistical analysis during long term acoustic emission monitoring on a pre-stressed concrete beam. Corros. Sci. 2013, 73, 161–171. [Google Scholar] [CrossRef]
- Mangual, J.; ElBatanouny, M.; Ziehl, P.; Matta, F. Acoustic-emission-based characterization of corrosion damage in cracked concrete with prestressing strand. ACI Mater. J. 2013, 110, 89–98. [Google Scholar]
- ElBatanouny, M.; Ziehl, P.; Larosche, A.; Mangual, J.; Matta, F.; Nanni, A. Acoustic emission monitoring for assessment of prestressed concrete beams. Constr. Build. Mater. 2014, 58, 46–53. [Google Scholar] [CrossRef]
- Abdelrahman, A.; ElBatanouny, M.; Ziehl, P.; Fasl, J.; Larosche, C.J.; Fraczek, J. Classification of alkali-silica reaction damage using acoustic emission: A proof-of-concept study. Constr. Build. Mater. 2015, 95, 406–413. [Google Scholar] [CrossRef]
- Laroche, A.; Ziehl, P.; Mangual, J. Damage evaluation of prestressed piles to cast in pace bent cap connections with acoustic emission. Eng. Struct. 2015, 84, 184–194. [Google Scholar] [CrossRef]
- Abdelrahman, M.; ElBatanouny, M.; Rose, J.; Ziehl, P. Signal processing techniques for filtering acoustic emission data in prestressed concrete. Struct. Health Monit. in press.
- Benavent-Climent, A.; Castro, E.; Gallego, A. Evaluation of low cycle fatigue damage in RC exterior beam-column subassemblages by acoustic emission. Constr. Build. Mater. 2010, 24, 1830–1842. [Google Scholar] [CrossRef]
- Sagasta, F. Evaluación De Daño En Estructuras De Hormigón Armado Sometidas a Cargas Sísmicas Mediante El Método De Emisión Acústica. Ph.D. Thesis, Universidad de Granada, Granada, Spain, 29 January 2016. [Google Scholar]
- Benavent-Climent, A.; Escolano-Margarit, D.; Morillas, L. Shake-table tests of a reinforced concrete frame designed following modern codes: Seismic performance and damage evaluation. Earthq. Eng. Struct. Dyn. 2014, 43, 791–810. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Gallego, A.; Vico, J.M. An acoustic emission energy index for damage evaluation of reinforced concrete slabs under seismic loads. Struct. Health Monit. 2011, 11, 69–81. [Google Scholar] [CrossRef]
- Zitto, M.E.; Piotrkowski, R.; Gallego, A.; Sagasta, F.; Benavent-Climent, A. Damage assessed by Wavelet scale bands and b-value in dynamical test of a reinforced concrete slab monitored with acoustic emission. Mech. Syst. Signal Process. 2015, 60, 75–89. [Google Scholar] [CrossRef]
- Zitto, M.E.; Piotrkowski, R.; Gallego, A.; Sagasta, F. AE wavelet processing in dynamical tests of a reinforced concrete slab. J. Acoust. Emiss. 2012, 30, 64–75. [Google Scholar]
- Sagasta, F.; Torné, J.L.; Sánchez, A.; Gallego, A. Discrimination of acoustic emission signals for damage assessment in a reinforced concrete slab subjected to seismic simulations. Arch. Acoust. 2013, 38, 303–310. [Google Scholar] [CrossRef]
- Sagasta, F.; Morillas, L.; Roldán, A.; Benavent-Climent, A.; Gallego, A. Discrimination of AE signals from friction and concrete cracking in a reinforced concrete frame subjected to seismic trainings. In Proceedings of the 6th ECCOMAS Conference on Smart Structures and Materials SMART2013, Turin, Italy, 24–26 June 2013.
- Sagasta, F.; Benavent-Climent, A.; Fernández-Quirante, T.; Gallego, A. Modified Gutenberg-Richter coefficient for damage evaluation in reinforced concrete structures subjected to seismic simulations on a shaking table. J. Nondestruct. Eval. 2014, 33, 616–631. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Soulioti, D.V.; Getselou, E.A.; Barkoula, N.M.; Matikas, T.E. Monitoring of the mechanical behavior of concrete with chemically treated steel fibers by acoustic emission. Constr. Build. Mater. 2013, 48, 1255–1260. [Google Scholar] [CrossRef]
- Japanese Industrial Standards (JIS) A 1132. In Method of Making and Curing Concrete Specimens; Japan Concrete Institute Standard: Tokyo, Japan, 2014.
- Luo, Y.H.; Durrani, A.J. Equivalent beam model for flat-slab buildings—Part II: Exterior connections. ACI Struct. J. 1995, 92, 250–257. [Google Scholar]
- Scribner, C.F.; Wight, J.K. Strength decay in reinforced concrete members under load reversals. J. Struct. Division ASCE 1980, 106, 861–875. [Google Scholar]
- Benavent-Climent, A.; Morillas, L.; Escolano, D. Seismic performance and damage evaluation of a reinforced concrete frame with hysteretic dampers through shake-table tests. Earthq. Eng. Struct. Dyn. 2014, 43, 2399–2417. [Google Scholar] [CrossRef] [Green Version]
- Benavent-Climent, A.; Donaire-Ávila, J.; Oliver-Saiz, E. Shaking table tests of a reinforced concrete waffle-flat plat structure designed following modern codes: Seismic performance and damage evaluation. Earthq. Eng. Struct. Dyn. 2015. [Google Scholar] [CrossRef]
- Niccolini, G.; Borla, O.; Accornero, F.; Lacidogna, G.; Carpinteri, A. Scaling in damage by electrical resistance measurements: An application on the terracotta statues of the Sacred Mountain of Varallo Renaissance Complex (Italy). Rend. Lincei-Sci. Fis. 2015, 26, 203–209. [Google Scholar] [CrossRef]
- Niccolini, G.; Borla, O.; Lacidogna, G.; Carpinteri, A. Correlated fracture precursors in rocks and cement based materials under stress. In Acoustic, Electromagnetic, Neutron Emissions from Fracture and Earthquakes; Carpinteri, A., Lacidogna, G., Manuello, A., Eds.; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Carpinteri, A.; Lacidogna, G.; Manuello, A.; Borla, O. Electromagnetic and neutron emissions from brittle rocks failure: Experimental evidence and geological implications. J. SADHANA 2012, 37, 59–78. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Manuello, A.; Niccolini, A.; Schiavi, A.; Agosto, A. Mechanical and electromagnetic emissions related to stress-induced cracks. Exp. Tech. 2010, 36, 53–64. [Google Scholar] [CrossRef]
- Selman, E.; Ghiami, A.; Alver, N. Study of fracture evolution in FRP-strengthened reinforced concrete beam under cyclic load by acoustic emission technique: An integrated mechanical-acoustic energy approach. Constr. Build. Mater. 2015, 95, 832–841. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Castro, E.; Gallego, A. AE monitoring for damage assessment of RC exterior beam-column subassemblages subjected to cyclic loading. Struct. Health Monit. 2009, 8, 175–189. [Google Scholar] [CrossRef]
- Carpinteri, A.; Pugno, N. Fractal fragmentation theory for shape effects on quasi-brittle materials in compression. Mag. Concr. Res. 2002, 54, 473–480. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Niccolini, G. Critical behaviour in concrete structures and damage localization by acoustic emission. Key Eng. Mater. 2006, 312, 305–310. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Pugno, N. Structural damage diagnosis and life-time assessment by acoustic emission monitoring. Eng. Fract. Mech. 2007, 74, 273–289. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Niccolini, G. Fractal analysis of damage detected in concrete structural elements under loading. Chaos Soliton Fract. 2009, 42, 2047–2056. [Google Scholar] [CrossRef]





















© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sagasta, F.; Benavent-Climent, A.; Roldán, A.; Gallego, A. Correlation of Plastic Strain Energy and Acoustic Emission Energy in Reinforced Concrete Structures. Appl. Sci. 2016, 6, 84. https://doi.org/10.3390/app6030084
Sagasta F, Benavent-Climent A, Roldán A, Gallego A. Correlation of Plastic Strain Energy and Acoustic Emission Energy in Reinforced Concrete Structures. Applied Sciences. 2016; 6(3):84. https://doi.org/10.3390/app6030084
Chicago/Turabian StyleSagasta, Francisco, Amadeo Benavent-Climent, Andrés Roldán, and Antolino Gallego. 2016. "Correlation of Plastic Strain Energy and Acoustic Emission Energy in Reinforced Concrete Structures" Applied Sciences 6, no. 3: 84. https://doi.org/10.3390/app6030084
APA StyleSagasta, F., Benavent-Climent, A., Roldán, A., & Gallego, A. (2016). Correlation of Plastic Strain Energy and Acoustic Emission Energy in Reinforced Concrete Structures. Applied Sciences, 6(3), 84. https://doi.org/10.3390/app6030084