Design and Characterization of a Birefringent-Type Compact Displacement Sensor for Improving Measurement Sensitivity by a Guided-Wave Beam

Abstract

A compact displacement sensor (CDS) fabricated with the combinations of a birefringent KTP and cylindrical lens is proposed to be applied for optical displacement measurements in a common-path interferometer. To overcome the beam distortion issues of an original laser beam (OLB) in the small radius of the lens, a guided-wave beam (GWB) is proposed to demonstrate that the GWB (having better measurement characteristics than the OLB) is essential to achieve the improved sensitivity of displacement measurements performed by the CDS.

1. Introduction

Low divergence and a small spot light beam are essential for the displacement measurements made with a position sensitivity detector (PSD) [1]. PSD-based beam displacement measurements are important for various uses, including the atomic force microscope, the proximity exposure tool, the optical pickup head, and the Goos-Hänchen effect [2,3,4,5]. Incidentally, phase-interrogation due to optical length differences between the reference and sensing paths was proposed for displacement measurements in various interferometers [6,7]. The transformation between the incident angle and the displacement variations are made reversible using the cylindrical and object lenses [8,9]. The displacement of the probe light was converted to the propagation angle change through a prompt transducer. The angle variations can be characterized by an optical angle sensor. Surface plasmon resonance (SPR) and total internal reflection (TIR) sensors have been successfully demonstrated to measure the angle changes in a phase-interrogation heterodyne interferometer [8,9,10].

In optical metrology, birefringent materials have been widely utilized in the design of sensing transducers, particularly in angle, refractive index, spectra, and bio reaction sensors [11,12,13,14,15,16]. The phase delay between two orthogonal polarizations (s-and p-wave) is dependent on the incident angle, birefringence, relative refractive index, and wavelength. A prism with a birefringent calcite plate attached was evaluated based upon optical angle measurement [11]. The birefringent plate immersed in a liquid medium has been proposed for the optical angle and concentration sensors in our previous works [12,13,14]. To overcome the induced distortion of a large light beam being refracted on a curved surface, light beams with low divergence and a small spot are essential for improving measurement sensitivity; in this study, a guided-wave beam (GWB) is proposed to fulfill these requirements. A cylindrical lens with a potassium titanyl phosphate (KTP) plate attached was fabricated as a compact displacement sensor (CDS). According to the experimental results, the use of the GWB, having better measurement characteristics than the original light beam (OLB,) shows that its use is critical to the improved sensitivity of displacement measurements made by the CDS in a dual-channel homodyne interferometer. Finally, the achieved displacement sensitivity is around 1.49°/µm in displacement, ranging from 0 to 40 µm. According to the system stability of 0.007°, the resolution of 4.7 nm is available.

2. Principles of the Compact Displacement Sensor

Figure 1 shows the photo and geometric drawing of the proposed CDS for lateral displacement measurements. Figure 1a is the photo of the fabricated CDS showing the main dimensional sizes. As marked in the photo, the width and height of the cylindrical lens (LJ1155L1, Thorlab, Newton, NJ, USA) are 16 and 18 mm, respectively. The radius and focal length are 10.2 and 19.7 mm, respectively. In another cylindrical lens (Model LJ1909L1, Thorlab, Newton, NJ, USA), the width and height are 13 and 15 mm, respectively. The radius and focal length are 7.1 and 13.7 mm, respectively. The thickness and length of the square shape KTP plate are 1 and 10 mm, respectively. The same dimensional KTP plates were used for the two different cylindrical lenses. Figure 1b illustrates the ray traces and angle variations of the probe light in the CDS. A cylindrical lens (n2) was attached to the KTP (n4) using UV glue (n3). The probe light in the air (n1) was perpendicular to the flattened side of the cylindrical lens. The CDS was placed on a moveable micro-displacement piezoelectric transducer (PZT) stage (Model MAX312D/M, Thorlab, Newton, NJ, USA), and the probe light was fixed. The incident angle is changed with the displacement of PZT. O is the center of the cylindrical lens with a radius of OA = R. The probe light transmits onto the semispherical surface at position V. The extension line VL is parallel to OA, which is perpendicular to the flattened side OB of the CDS. The refractive angle through the KTP can be controlled depending on the probe beam positions. There are two initial positions, and the corresponding distances OL = 1/2H and 3/4H were used in the experiments. Therein, a half width of the cylindrical lens is expressed as OB = H. According to Snell’s law, the initial incident angle at the air-lens interface is defined by:

$${\theta }_{1i}=si{n}^{-1}\left(OL/R\right)$$

(1)

The relationships between the angle variations and the various refractive index layers in the different interfaces are represented as follows:

$${\theta }_{1r}=si{n}^{-1}(\frac{n_1}{n_2}\cdot \sin {\theta }_{1i})$$

(2)

$${\theta }_{2i}={\theta }_{1i}-{\theta }_{1r}; {\theta }_{2r}={\theta }_{3i}$$

(3)

$$n_2\cdot \sin {\theta }_{2i}=n_3\cdot sin{\theta }_{2r}$$

(4)

$$n_3\cdot sin{\theta }_{3i}=n_{4s}\cdot sin{\theta }_{3r\_s}=n_{4p}\cdot sin{\theta }_{3r\_p}$$

(5)

$$n_2\cdot sin{\theta }_{2i}=n_{4s}\cdot sin{\theta }_{3r_s}=n_{4p}\cdot sin{\theta }_{3r_p},$$

(6)

where $n_{4s}$ and $n_{4p}$ are the effective refractive indices of s-and p-waves in the KTP, respectively, and ${\theta }_{3r\_s}$ and ${\theta }_{3r\_p}$ are the corresponding refractive angles of s-and p-waves respectively.

According to Equations (4)–(6), the effect from the glue layer can be ignored in considering the measurement sensitivity of the angle and displacement. In this CDS, the phase delay $\varphi$ between two orthogonal polarizations is dependent on the thickness of the KTP plate, incident angle, and relative refractive index, as discussed in a previous study [12]. The $\varphi$ is defined by

$$\varphi =\frac{2\pi }{\lambda }·d·\left[\sqrt{n_z^2-n_2^2·si{n}^2{\theta }_{2i}}-\sqrt{n_y^2-n_2^2·\left(\frac{n_y^2}{n_x^2}\right)·si{n}^2{\theta }_{2i}}\right].$$

(7)

The angle sensitivity (AS) of the CDS is represented by

$$\mathrm{AS}=\frac{d\varphi }{d{\theta }_{2i}}=\frac{2\pi }{\lambda }·d·n_2^2·sin{\theta }_{2i}·cos{\theta }_{2i}·\left[\frac{n_y^2}{n_x^2·\sqrt{n_y^2-n_2^2·\left(\frac{n_y^2}{n_x^2}\right)·si{n}^2{\theta }_{2i}}}-\frac{1}{\sqrt{n_z^2-n_2^2·si{n}^2{\theta }_{2i}}}\right],$$

(8)

where λ and d are the measurement wavelength and thickness of the KTP plate, respectively. Three different refractive indices of the KTP plate are n_x, n_y, and n_z [12]. At the same CDS, the AS is adjustable according to the ${\theta }_{2i}$ by controlling the initial incident positions. According to Equations (1)–(3), the angle variation $d{\theta }_{2i}$ induced from the small displacement dL can be represented by

$$d{\theta }_{2i}=\frac{1}{R}\cdot \left[\frac{1}{cos{\theta }_{1i}}-\frac{n_1}{\sqrt{n_2^2-n_1^2\cdot sin{\theta }_{1i}^2}}\right]\cdot dL$$

(9)

By calculating Equations (8) and (9), the displacement sensitivity (DS) is defined by

$$\mathrm{DS}=\frac{d\varphi }{dL}=\mathrm{AS}\cdot \frac{1}{R}\cdot \left[\frac{1}{cos{\theta }_{1i}}-\frac{n_1}{\sqrt{n_2^2-n_1^2\cdot sin{\theta }_{1i}^2}}\right]$$

(10)

3. Measurement Setup

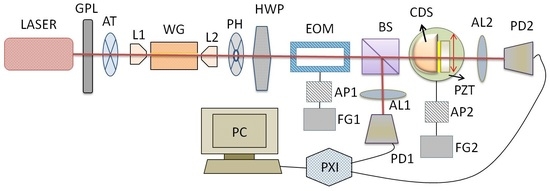
To compare the displacement measurement performance depending on the characteristics of a beam spot, therein the OLB from a stabilized He-Ne laser with a wavelength of 632.8 nm (Model R-32734, Newport Corporation, Irvine, CA, USA), and the measurement setup shown in Figure 2 based on the dual-channel homodyne interferometer [17], was used. The OLB with a vertical polarization was obtained using a Glan-Thompson polarizer (GPL). A half-wave plate (HWP) at an azimuth angle of 22.5° was used to obtain two orthogonal polarizations of equal amplitude. The input optical power was controlled using an attenuator (AT). An electro-optic modulator EOM (Model 4002 New Focus, Newport Corporation, Irvine, CA, USA) was used to modulate the phase delay between the two polarizations. The EOM was driven by a function generator (FG1) and voltage amplifier (AP1). The amplitude and frequency of the applied sinusoidal voltage were 105 V and 1 kHz, respectively. The voltage induces the corresponding phase modulations used in the homodyne interferometry. The incident light was divided into two paths via a non-polarization beam splitter (BS). The reflected light passing through an analyzer (AL1) was received by a photodetector (PD1). The reflected signal was used to monitor the photorefractive induced phase noise from the EOM. The CDS was placed on the PZT stage driven by a function generator (FG2) and a voltage amplifier (AP2). According to the product specifications from the vender, displacement is around 40 µm at an applied voltage of 150 V onto the stage. The transmitted light passed through the CDS, and an analyzer (AL2) was then received by a photodetector (PD2). The transmitted light was used to measure the phase variations caused by the displacement. Both the interferometric signals of the reflected and transmitted paths were connected to a multichannel data acquisition module (PXI). A fast Fourier transform (FFT) scheme was adopted to decide the measured phase variations [18], and this phase information was displayed on a personal computer (PC). The common phase noise can be effectively reduced by synchronously measuring the phase variations of both channels [17].

In comparison with the measurement provided by the OLB, the GWB was formed through the measurement setup shown in Figure 3. The same He-Ne laser was used for the measurements. The laser beam was modified by the setup consisting of a channel waveguide device (WG), and two coupled object lenses (L1 and L2). To fabricate a single-mode waveguide for TE and TM polarizations as developed in our research works [17,18], a 35 nm Zn film with a predeposition Ni film of 5 nm was deposited over the lithium niobate substrate via e-beam evaporation. Next, the waveguide width of 4 µm was formed by a lift-off technique. After thermal diffusion of 850 °C for 120 min, the Zn ions penetrate the host substrate and form a graded index distribution in the lateral and in-depth directions. The substrate end faces were polished for the light coupling. The two lenses L1 and L2 were used to focus the input and output light beams. A pinhole (PH) was used to block the scattering light. The functions of GPL, AT, and HWP are the same as described in Figure 2. In case of the GWB measurements, both of the WG and EOM are the lithium niobate materials. Therefore, the AT is placed in front of the WG. A series of experiments was conducted to compare the measurement performance between the OLB and GWB.

4. Discussion

Figure 4 shows performance comparisons of the beam profiles and system stability of the OLB and the GWB. The single-mode waveguide is like a spatial filter, and the end-fire coupling object lenses were used to obtain the low divergence and small spot probe beam. According to the measured beam profiles, as shown in Figure 4a, the GWB has a more confined and symmetrical distribution than the OLB does. The sizes of half-power beam width (HPBW) are around 0.43 and 0.38 mm for the OLB and GWB, respectively. The system stability was then tested in the dual-channel homodyne interferometer. The phase variations after subtraction between two channels were measured, as shown in Figure 4b. In a measuring period of 360 sec, the stabilities based on the values of root mean square (RMS) are 0.009° and 0.007° for the OLB and GWB, respectively. In comparing the GWB with the OLB, the system stability is improved slightly by the GWB.

To further compare the measurement characteristics of optical displacement for the GWB and OLB using the same CDS and incident positions, the phase responses to displacement when different voltages were applied on the PZT were measured. Figure 5 represents the phase responses for the different applied sawtooth voltages using the GWB at incident positions 1/2H and 3/4H on the CDS of R = 10.2 mm. Thus, the incident angles ${\theta }_{1i}$ are 15° and 22.8° for incident positions 1/2H and 3/4H, respectively. The incident angles ${\theta }_{2i}$ are 8.1° and 13.2° for incident positions 1/2H and 3/4H, respectively. At position 1/2H, the maximum phase variations are 5.2°, 7.2°, and 9.8° for the three applied voltages 75, 100, and 150 V, respectively, as shown in Figure 5a. At position 3/4H with the previous three voltages applied, Figure 5b presents the maximum phase variation: 10.7°, 13.7°, and 20.1°. To compare the measurement performance of the GWB, a series of experiments with the same applied voltages, CDS, and incident positions were evaluated by the OLB. The results of phase responses are shown in Figure 6. At position 1/2H, the phase variations are 4.2°, 5.6°, and 7.8° for the three applied voltages 75, 100, and 150 V, respectively, as shown in Figure 6a. At position 3/4H with the previous three voltages, Figure 6b presents the phase variations: 10.1°, 12.3°, and 17.4°. Figure 7 summarizes the phase variation versus the voltage of the GWB and OLB at the different incident positions. The results show that the GWB can obtain higher slopes than the OLB can at both incident positions. It is reasonable to assume that the GWB with its low divergence and small spot can improve measurement stability when passing through a curved surface.

Based on the confirmed evidence, the CDS with the smaller radius of 7.1 mm was further adopted to test the phase response for the different positions shown in Figure 8. Thus, the incident angles ${\theta }_{1i}$ are 17.6° and 26.9° for the incident positions 1/2H and 3/4H, respectively. The incident angles ${\theta }_{2i}$ are 9.6° and 16.4° for the incident positions 1/2H and 3/4H, respectively. At the position of 1/2H, the maximum phase variations are 8.5°, 11.1°, and 15.3° for the three applied voltages of 75, 100, and 150 V, respectively, as shown in Figure 8a. At the position 3/4H with the previous three voltages, Figure 8b presents the phase variations: 22.1°, 27.7°, and 37.8°. The position selections of 1/2H and 3/4H are just used for comparing the phase response dependence on the initial positions. The adjustable displacement sensitivities are considered for the different dynamic measurement ranges. Because the received power of the refracted light is decreased dramatically when the incident positions over 3/4H on the CDS of R = 7.1 mm, it means that the initially maximum positions are still limited by the beam divergence effect on the curved surface.

The compared results of the phase responses dependent on the different radii of CDS are shown in Figure 9. The smaller radius and larger incident distances can increase phase variations under the same applied voltage. This means that the displacement sensitivity is enhanced along with measurement resolution being increased. Based on simulations as discussed in Refs. [8,9], use of a smaller radius in a cylindrical lens can achieve higher sensitivity. However, their demonstration experiments used cylindrical lenses with radii of 10 and 25 mm only. The main concern is that the beam spot from the original laser is too large when the lens radius is smaller than 10 mm. Actually, we tried the OLB for measuring the phase response of CDS (R = 7.1 mm). However, the results show that the repeatability and displacement sensitivity are both worse compared to the GWB. According to our experimental results, the design of CDS is important and the GWB is essential to improve the measurement sensitivity by employing the small radius of CDS. Moreover, the proposed GWB plays a key role for the repeatable measurements.

In previous experiments, the CDS was fabricated using only a single KTP plate (1-KTP) attached to the cylindrical lens since phase variation is also proportional to the thickness of the KTP plate. Furthermore, a CDS made of two adhesive KTP plates (2-KTP) was explored to compare measurement sensitivity with that of a CDS using 1-KTP. Figure 10 shows the relationship between the phase variation and the applied voltage using the CDS with R = 7.1 mm and 2-KTP plates. At position 1/2H, the maximum phase variations are 13.1°, 16.7°, and 22.2° for the three applied voltages 75, 100, and 150 V, respectively, as shown in Figure 10a. At position 3/4H with the previous voltage conditions, Figure 10b presents the phase variations: 27.7°, 36.9°, and 58.3°. The summarized results of phase-to-applied-voltage at different incident positions for the CDS of R = 7.1 mm with the different 1-KTP and 2-KTP plates shown in Figure 11. Figure 12 shows the summarized results of phase versus displacement at the 3/4H position for the different CDSs when the PZT stage has 150 V applied (displacement = 40 µm).

The slope and R-square after a linear fit on these phase curves can be further calculated to compare performance on the different CDSs. The slope is expressed as average displacement sensitivity. In comparing the different radii of 1-KTP CDS probed by the GWB at the position 3/4H, according to Equation (10), the simulation values of DS are 0.45 and 0.98°/µm and the experimental values are 0.49 and 0.99°/µm for R = 10.2 mm and R = 7.1 mm, respectively. The close proximity of values in the simulations and the experiments indicate that the fabrication and application of the 1-KTP CDS are easily achievable. The largest slope of 1.49°/µm in displacement ranging from 0 to 40 µm with R-square of 0.9998 was achieved when probed by the GWB at the position 3/4H on the 2-KTP CDS of R = 7.1 mm. The system phase stability is around 0.007°, and the resolution of 4.7 nm is achievable. In an ideal situation, the slope of the phase curve shall be around 1.96°/µm due to the increased (double) thickness of the KTP plate in the 2-KTP CDS. However, the experimental value of 1.49°/µm is smaller than the simulation value of 1.96°/µm. The increased thickness of KTP plates gradually induces the non-ignored walk-off between two orthogonal polarizations to possibly reduce the DS. This means that the KTP plate will be optimized for the maximum thickness.

5. Conclusions

The design and characterization of the proposed birefringent-type compact displacement sensor (CDS) has been systematically studied to demonstrate the improved measurement sensitivity by employing the guided-wave beam (GWB) in a dual-channel homodyne interferometer. In comparison with the original laser beam (OLB), the low divergence and small spot GWB can be used for the small radius of the CDS. A series of experiments was conducted to evaluate measurement performance using CDSs with different radii and numbers of KTP layers when probed at two different positions. By using the CDS of 2-KTP at the position 3/4H, the achieved displacement sensitivity is around 1.49°/µm in displacement ranging from 0 to 40 µm with the R-square of 0.9998 after a linear fit. According to the system stability of 0.007°, the resolution of 4.7 nm is available.