Modeling and Finite Element Analysis of Load-Carrying Performance of a Wind Turbine Considering the Influence of Assembly Factors
Abstract
:1. Introduction
2. Case Study
3. Key Influencing Factors
3.1. Assembly Clearance
3.2. Machining Deviation
3.3. Propel Stroke
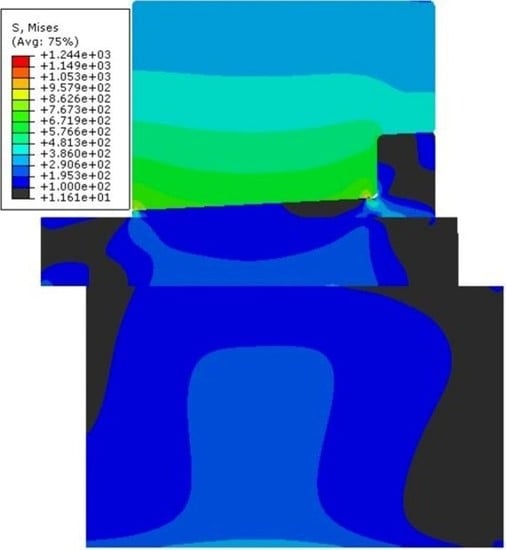
4. Finite Element Model
5. Test Verification
6. Results and Discussions
6.1. Assembly Clearance
6.2. Machining Deviations
6.3. Propel Travel
6.4. Performance of the Models
7. Conclusions
- (1)
- The theoretical model and finite element model of the turbine shrink disk were constructed, and a test device has been developed to verify the reasonability of the proposed models for load-carrying performance evaluation.
- (2)
- Different assembly clearances have different effects on the load-carrying performance of a turbine shrink disk. The maximum assembly clearance has a large effect on the contact pressure of the mating surfaces and the load torque, whereas the effect of the minimum assembly clearance is relatively small. The effect of the assembly clearance must be taken into consideration during the design and calculation, and the assembly clearance should be reasonably determined.
- (3)
- Machining deviation has a relatively small effect on the contact pressure and load torque of the mating surfaces. If the machining deviation is within reasonable range, then the load-carrying performance of a multiple-layer interference fit can be ensured.
- (4)
- The propel stroke has a significant effect on the contact pressure of the mating surface and the load torque. To avoid the abnormal operation of equipment caused by insufficient load torque, the propel stroke during practical assembly should be at least 0.95 times that of the designed propel stroke.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Biron, G.; Vadean, A.; Tudose, L. Optimal design of interference fit assemblies subjected to fatigue loads. Struct. Multidiscip. Optim. 2013, 47, 441–451. [Google Scholar] [CrossRef]
- Chakherlou, T.; Mirzajanzadeh, M.; Vogwell, J. Experimental and numerical investigations into the effect of an interference fit on the fatigue life of double shear lap joints. Eng. Fail. Anal. 2009, 16, 2066–2080. [Google Scholar] [CrossRef]
- Truman, C.; Booker, J. Analysis of a shrink-fit failure on a gear hub/shaft assembly. Eng. Fail. Anal. 2007, 14, 557–572. [Google Scholar] [CrossRef]
- Manuel, P.; Naoufel, N.; Marc, S. Study of an interference fit fastener assembly by finite element modeling, analysis and experiment. Int. J. Interact Des. Manuf. 2012, 6, 171–177. [Google Scholar]
- Boutoutaou, H.; Bouaziz, M.; Fontaine, J. Modeling of interference fits taking form defects of the surfaces in contact into account. Mater. Design 2011, 32, 3692–3701. [Google Scholar] [CrossRef]
- Mack, W.; Plöchl, M. Transient heating of a rotating elastic–plastic shrink fit. Int. J. Eng. Sci. 2000, 38, 921–938. [Google Scholar] [CrossRef]
- Jahed, H.; Farshi, B.; Karimi, M. Optimum autofrettage and shrink-fit combination in multi-layer cylinders. J. Pressure Vessel Tech. 2006, 128, 196–200. [Google Scholar] [CrossRef]
- Sogalad, I.; Ashokaa, H. Influence of cylindricity and surface modification on load bearing ability of interference fitted assemblies. Precision Eng. 2012, 36, 629–640. [Google Scholar] [CrossRef]
- Cheng, D.X. Handbook of Mechanical Design, Connection and Fastening; Chemical Industry Press: Beijing, China, 2004; Volume 2, pp. 276–290. [Google Scholar]
- Wang, J.; Tang, L. Shrink Disk Design Theory and Methodology; Metallurgical Industry Press: Beijing China, 2014; Volume 2, p. 41. [Google Scholar]
- Zhang, H.; Liao, A.; Wu, C. Numerical simulation of contact problems in vane machinery by a parametric quadratic programming method. Arch. Appl. Mech. 2007, 77, 421–437. [Google Scholar] [CrossRef]
- Wang, J.; Tao, D.; Huang, Q. Algorithm research on contact pressure and magnitude of interference for multi-layer cylinder’s interference fit. Eng. Mech. 2013, 30, 270–275. [Google Scholar]
- Özel, A.; Temiz, S.; Aydin, M.; Şen, S. Stress analysis of shrink-fitted joints for various fit forms via finite element method. Mater. Design 2005, 26, 281–289. [Google Scholar] [CrossRef]
- Sun, M.; Lu, S.; Li, D.; Li, Y.; Lang, X.; Wang, S. Three-dimensional finite element method simulation and optimization of shrink fitting process for a large marine crankshaft. Mater. Design 2010, 31, 4155–4164. [Google Scholar] [CrossRef]
- Zeng, F.; Chen, G.; Zhou, Z. Fretting analysis of interference fitting of wheel-set based on ANSYS. J. Mech. Eng. 2011, 47, 121–125. [Google Scholar] [CrossRef]
- Pedersen, P. On shrink fit analysis and design. Comput. Mech. 2006, 37, 121–130. [Google Scholar] [CrossRef]
- Wang, J.; Kang, J.; Tang, L. Theoretical and experimental studies for wind turbine’s shrink disk. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2015, 229, 325–334. [Google Scholar]
- Zhang, X.; Shao, J.; An, W.; Yang, T.; Malekian, R. An improved time-frequency representation based on nonlinear mode decomposition and adaptive optimal kernel. Elektron. Elektrotech. 2016, 22, 52–57. [Google Scholar]
- Jin, X.; Shao, J.; Zhang, X.; An, W.; Malekian, R. Modeling of nonlinear system based on deep learning framework. Nonlinear Dy. 2016, 84, 1327–1340. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, N.; Malekian, R.; Wang, R.; Li, P. TMicroscope: Behavior perception based on the slightest RFID tag motion. Elektron. Elektrotech. 2016, 22, 114–122. [Google Scholar] [CrossRef]
- Malekian, R.; Bogatinoska, D.C.; Karadimce, A.; Trengoska, J.; Nyako, W.A. A novel smart ECO model for energy consumption optimization. Elektron. Elektrotech. 2015, 21, 75–80. [Google Scholar]
- Prabu, K.; Kumar, D.S.; Malekian, R. BER Analysis of BPSK-SIM-based SISO and MIMO FSO systems in strong turbulence with pointing errors. Opt. Inter. J. Light Electron. Opt. 2014, 125, 6413–6417. [Google Scholar] [CrossRef]
- Modieginyane, K.M.; Letswamotse, B.B. Software defined wireless sensor networks (SDWSNs) application opportunities for efficient network management: A survey. Comput. Electr. Eng. J. (in press).
- Wang, Z.; Ye, N.; Xiao, F.; Wang, R. TrackT: Accurate tracking of RFID tags with mm-level accuracy using first-order taylor series approximation. AD Hoc Netw. 2016, 53, 132–144. [Google Scholar] [CrossRef]
- Shao, J.; Wang, L.; Zhao, W.S.; Zhong, Y.Q. An improved synchronous control strategy based on fuzzy controller for PMSM. Elektron. Elektrotech. 2014, 20, 17–23. [Google Scholar]








| Model Category | Model Number | Assembly Clearance (mm) | Machining Deviation (mm) | Propel Stroke (mm) | |
|---|---|---|---|---|---|
| Mating Surface of the Shaft and the Sleeve | Mating Surface of the Sleeve and the Inner Ring | Mating Surface of the Inner Ring and the Outer Ring | |||
| Assembly clearance | 1# | 0 | dA, dB, dC, dD | BD | |
| 2# | 0.022 | 0.08 | |||
| 3# | 0.136 | 0.24 | |||
| Machining deviation | 4# | 0 | dA − 0.062, dB − 0.062 dC + 0.062, dD + 0.062 | ||
| 5# | dA + 0.062, dB + 0.062 dC − 0.062, dD − 0.062 | ||||
| Propel stroke | 6# | 0 | dA, dB, dC, dD | BD1 | |
| 7# | BD2 | ||||
| Parameters | Value |
|---|---|
| Inside diameter of shaft, d0 (mm) | 60 |
| Diameter of the mating surfaces of shaft and sleeve, d1 (mm) | 520 |
| Diameter of the mating surfaces of sleeve and inner ring, d2 (mm) | 640 |
| Average diameter of long conical surfaces of inner ring, d3 (mm) | 663.715 |
| Outside diameter of outer ring, d4 (mm) | 1020 |
| Length of the contact surface of shaft and sleeve, l1 (mm) | 255 |
| Rated torque on mating surface of shaft and sleeve, M (N·m) | 2800 |
| Material elastic modulus of shaft, inner ring and outer ring (GPa) | 210 |
| Material elastic modulus of sleeve (GPa) | 180 |
| Poisson‘s ratio | 0.300 |
| Torque Value T (kN·m) | Circumferential Slip (S/mm) | Holding Pressure Time (t/min) |
|---|---|---|
| 0.4T0 | 0 | 3 |
| 0.5T0 | 0 | 3 |
| 0.65T0 | 0 | 3 |
| 0.8T0 | 0 | 3 |
| T0 | 0 | 3 |
| 1.2T0 | 0 | 3 |
| Model Number | Torque (kN·m) | Relative Error (%) |
|---|---|---|
| 1# | 3396 | 0.0 |
| 2# | 3245 | 4.4 |
| 3# | 2599 | 23.5 |
| 4# | 3233 | 4.8 |
| 5# | 3565 | 5.0 |
| 6# | 2675 | 21.2 |
| 7# | 3033 | 10.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Ning, K.; Tang, L.; Malekian, R.; Liang, Y.; Li, Z. Modeling and Finite Element Analysis of Load-Carrying Performance of a Wind Turbine Considering the Influence of Assembly Factors. Appl. Sci. 2017, 7, 298. https://doi.org/10.3390/app7030298
Wang J, Ning K, Tang L, Malekian R, Liang Y, Li Z. Modeling and Finite Element Analysis of Load-Carrying Performance of a Wind Turbine Considering the Influence of Assembly Factors. Applied Sciences. 2017; 7(3):298. https://doi.org/10.3390/app7030298
Chicago/Turabian StyleWang, Jianmei, Ke Ning, Liang Tang, Reza Malekian, Yinan Liang, and Zhixiong Li. 2017. "Modeling and Finite Element Analysis of Load-Carrying Performance of a Wind Turbine Considering the Influence of Assembly Factors" Applied Sciences 7, no. 3: 298. https://doi.org/10.3390/app7030298
APA StyleWang, J., Ning, K., Tang, L., Malekian, R., Liang, Y., & Li, Z. (2017). Modeling and Finite Element Analysis of Load-Carrying Performance of a Wind Turbine Considering the Influence of Assembly Factors. Applied Sciences, 7(3), 298. https://doi.org/10.3390/app7030298