Grain Size in Aluminum Alloy 6061 under Hot Ring Compression Test and after T6 Temper

Abstract

Peripheral coarse grain during and after hot forming is often a major inconvenience for manufacturing aluminum alloy parts. Not only is the strength reduced, but the subsequent surface treatments are also hard to realize. The literature has shown that peripheral coarse grain is very likely induced by the previous process, such as extrusion. To investigate if peripheral coarse grain could be caused solely by hot forming, this study removed the billet surface layers. This eliminates the effect from the previous processes preparing the billets and forms ring specimens for executing ring compression test. The ring compression test can reveal the friction circumstance of the specimen to the die surface and create versatile deformation in the specimens to simulate forging situations, thereby providing multifaceted conditions to develop diverse grain size in specimen, particularly on its surface. The experiments were designed and analyzed under the Taguchi method, with consideration for factors such as working temperature, speed and amount of compression, and lubricant. Under each experiment, no peripheral coarse grains were found in the specimen, which were peeled and compressed, and even the average grain size after compression test is larger than that of the received billet. No peripheral coarse grains were found in the subsequent T6 temper either, which could, however, refine the grains.

1. Introduction

Formerly, materials used in structures were mostly steel based, because steel is easy to acquire, high in strength, and low in cost. However, aluminum alloy has a density about one third as much as steel. In addition, aluminum alloy has characteristics better than steel, such as high electrical and thermal conductivity, light weight, and simple to process. All these qualities have already made aluminum alloy a popular material for many applications, like transportation, the defense industry, automation and general household industries. In recent years, countries around the world are increasingly concerned about the issue of environmental protection. Because of excellent recycling characteristics, and under the trends of green manufacturing in less carbon and reducing waste, aluminum alloy is favored by industries to develop more diverse applications.

Although there are two categories of cast and wrought aluminum alloys, in most applications the parts are made from wrought materials. To manufacture such parts, raw aluminum alloys are heated in furnace and then placed on the die, and the punch moves toward the die to squeeze the alloys by carefully controlling the metal flow. This not only can easily form the alloys into the desired shape by plastic deformation, but can also enhance the mechanical properties of the alloys to achieve better strength. However, an incorrect process setup or improper temperature control can often result in grain coarsening of aluminum alloys, which can reduce the strength of the alloys or more likely cause them to break. Usually, the grain coarsening occurs on the surface of parts [1,2], which brings the surface poor appearances and makes it difficult to process further. If the situation of peripheral coarse grain can be improved, not only can the alloys be strengthened but the surface treatment costs can also thus be reduced, which would help industries upgrade their market competitiveness.

The peripheral coarse grains are mostly found in aluminum extrusions. Sweet et al. [1] had found that they could be made by some extrusion speed, amount or rate, and temperatures just above recrystallization temperature, at irregularities such as corners or junctions in thickness. They also showed that there were no peripheral coarse grains found on non-recrystallization or full recrystallization. Peripheral coarse grain can also be enlarged by subsequent solid solution [2]. The higher the temperature of solid solution, the more the peripheral coarse grain. Not only does extrusion have peripheral coarse grain, but forging also has it after heat treatment, despite the extrusion billet showing no peripheral coarse grains [3,4].

Whether peripheral coarse grain could be solely caused by hot forming is still unclear. In view of this question, this study is designed to investigate by removing the billet surface layers to eliminate the effect from the previous processes preparing the specimen. Experimental study is then executed in different working temperatures and surface conditions, specifically the frictional boundary conditions. In order to master the frictional boundary conditions, this study attempted to use a ring compression test [5,6] with different lubricants to determine the friction coefficient. At the same time, the ring compression test can provide diverse non-uniform strain distributions, which may allow a glimpse into grain size change after hot forging processes and after subsequent heat treatments of aluminum alloys.

2. Materials and Methods

The ring compression test used in this study allows the study to concentrate on the influence of the hot forging process setups on the peripheral grain coarsening of the aluminum alloy forging parts.

2.1. Material

The materials used in experiments were commercially acquired extruded 6061 aluminum alloy tubes (Wan Sow Aluminum, Tainan, Taiwan), and were modified intentionally to have an inner diameter of 8 mm and an outer diameter of 19 mm.

Table 1. Chemical compositions of an aluminum alloy 6061.

Element	Si	Fe	Cu	Mn	Mg	Cr	Zn	Ti	Ni	Al
(wt %)	0.66	0.21	0.25	0.063	0.96	0.076	0.037	0.023	0.014	remaining

shows the chemical compositions. The geometry of tubes was deliberately chosen to not meet the experimental specifications described in [5,6] so that the potential peripheral coarse grains made from previous processes can be completely removed. The specimen was made from the raw tubes by making the outer diameter 18 mm, the inner diameter 9 mm and cutting to a thickness of 6 mm (the standard specimen geometry has the ratio of outside diameter, inside diameter, and thickness equal to 6:3:2). Thereafter, the specimen was ground with abrasive papers in number of 400, 800, and 1200, respectively, and polished with polishing pad with a suspension of 1 μm alumina powder. Figure 1 shows the prepared specimens.

2.2. Procedure

The ring compression test used flat dies, so that it can be treated as a free forging or upsetting process. The polished specimen was placed in a furnace (Risen Instrument, Taipei, Taiwan) and heated to the specified temperature above the recrystallization temperature of the material for more than 50 min to reach thermal equilibrium. The specimen was then taken out and placed between the flat dies for forging process. After compressing the specimen to the desired stroke, it was immediately removed and quenched in water to preserve the grain structure in the metal. After the specimen was completely cooled to the room temperature, the grain size was observed with microscope (Nikon, Tokyo, Japan). Figure 2 shows the schematic experiment procedure.

2.3. Equipment

The equipment used in this study was a computer-controlled universal testing machine (Hung Ta Instrument, Taichung, Taiwan), which was operated with a servo-driven hydraulic valve and had a forging capacity of 90 tons. To heat and insulate the flat dies and forging ambient temperature, around the dies a tubular furnace (Risen Instrument, Taipei, Taiwan) was installed, which could provide a controllable temperature up to 1200 °C with a K-type thermocouple monitoring the temperature. The upper and lower die was made with SKD 11 and SKD 61, respectively, and heat treated to a hardness of HRC 50 or more. To prevent potential adverse impacts onto the structure of the testing machine, jackets with circulating water were mounted onto the ram and base plate of the testing machine, respectively, as shown in Figure 3.

2.4. Parameters

Based on the potential causes of grain coarsening mentioned in [1,2,3,4], this study set working temperature, upsetting speed, compression amount, and lubricant as experiment parameters that might influence the evolution of grain structures. Because the equipment used in experiments was designed not for high-speed forging, the upsetting speed was set to 0.36, 3.6, and 36 mm/min. The working temperature was assigned to be at 400, 450, and 500 °C from the suitable temperature range for forming 6061 aluminum alloy. The die temperature was fixed at 150 °C according to common factory settings. The compression amount was specified as 1, 2, and 3 mm, while the lubricant applied to the specimen for the frictional boundary condition between die and workpiece was selected without lubrication, graphite, and molybdenum disulfide (MoS₂).

2.5. Setups

In order to make the study more efficient and reduce the number of experiments, Taguchi method [7] was used to further simplify the experiment. The four parameters, each with three levels arranged above, were then formed into an L9 (3⁴) orthogonal table [8].

Table 2. Experiment setup an L9 (3⁴) orthogonal table.

Experiment no.	1	2	3	4	5	6	7	8	9
temperature (°C)	400	400	400	450	450	450	500	500	500
speed (mm/min)	0.36	3.6	36	0.36	3.6	36	0.36	3.6	36
compression (mm)	1	2	3	2	3	1	3	1	2
lubricant	none	graphite	MoS2	MoS2	none	graphite	graphite	MoS2	none

lists 9 experiments, each with its level for each factor (parameter).

2.6. Specimen for Metallography

After hot upsetting, the specimen was cut, mounted, and ground as well as polished. For the mounting operation, cold mounting resin was used. The resin was created by a specific process in which epoxy resin and hardener (Chung Shing Chemicals, Taichung, Taiwan) were blended in a ratio of 50:1, poured into a tubular mold with an inner diameter of 28 mm and height of 15 mm high tube mold, and put aside at room temperature for at least 8 h for curing. The mounted specimen was subsequently ground and polished to obtain a mirror surface as described above. Its surface was then etched with hydrofluoric acid (HF) (Choneye Pure Chemicals, Taipei, Taiwan) at a concentration of 22%. A metallurgical microscope with an image capture system was used to catch the grains images.

2.7. Grain Size Measurement

In this study, the grain size is expressed as the average grain diameter by using the linear intercept method, under which several circles with a known radius are drawn on a metallographic image and the number of intercepts between the circles and the grains is then counted. The average grain diameter is then determined by dividing the total length of circles with the total number of intercepts and magnification of image and by multiplying by 1.5 for assuming spherical grains [9]. Figure 4 shows the microstructure of the specimen made from the incoming alloy, which has the average grain size of 237 μm. There were no peripheral coarse grains found in the specimen. Fibrous grains elongated as mentioned in [1,2] were not found in any direction of the specimen either. The material of the specimen was believed to have recrystallized before shipment.

3. Results

3.1. Friction Coefficient

In this study, the influence of working temperature, upsetting speed, compression amount, and lubricant on the grain size were studied by using ring compression test. However, the friction coefficient for each experiment setup can be determined by computing the ratio of diameter to thickness of the specimen [5] as shown in

Table 3. Friction coefficient for each experiment setup determined according to [5] and its S/N ratio determined by Taguchi method.

Experiment No.	1	2	3	4	5	6	7	8	9
friction coefficient	0.25	0.20	0.17	0.20	0.27	0.22	0.20	0.18	0.27
S/N (dB)	12.0	14.0	15.4	14.0	11.4	13.2	14.0	14.9	11.4

.

Although the friction coefficients shown in Table 3 are almost the same, if they are regarded as quality characteristics y as per Taguchi method, they possess the smaller-the-better property, which indicates the idea that the lower the friction coefficient, the more uniform the deformation. By means of signal-to-noise (S/N) ratio, which is also shown in Table 3 and defined as

$$\mathrm{S}/\mathrm{N}=-10\log \frac{1}{n}{\displaystyle \sum _{i=1}^n{y}_i^2},$$

(1)

it can be observed that they are a little bit different. Based on Taguchi method, if the S/N ratios shown in Table 3 are averaged for each level of each factor, a response table can be obtained (

Table 4. Response table of factors and their levels on friction coefficient based on signal-to-noise (S/N) ratio (unit: dB) determined by Taguchi method.

Level No.	Factor
	Temperature	Speed	Compression	Lubricant
1	13.8	13.3	13.4	11.6
2	12.8	13.4	13.1	13.7
3	13.4	13.3	13.6	14.8
effect	1.0	0.1	0.5	3.2

) that describes the influence of each level of each factor on the quality characteristics. The greater the effect or the difference of S/N ratios between the levels of the same factor, the greater the influence of that factor on the quality characteristics. From Table 4, it can be observed that the effect of lubricant on the friction coefficient is the most significant (3.2 dB), followed by the working temperature (1.0 dB). The weakest effect is the upsetting speed (0.1 dB).

Although the response table described above can exhibit how qualitatively significant the influence of the factor is on the quality characteristics, it is still not easy to quantitatively determine their influence strength. A statistical analysis of variance (ANOVA) is therefore needed. From Table 4, the mean value of the S/N ratio for each factor can be calculated at the same time. The sum of squares (SS) of deviations of each level from the mean of the factor can then be obtained as the variance for the factor. If the sum of squares is divided by degree of freedom (DF), which is the number of levels minus 1, the mean square (MS) or variance for the factor can be determined. The contribution (% C) of each factor to the quality characteristics was calculated by means of ANOVA, and the importance of each factor was also determined, as shown in

Table 5. Analysis of variance in friction coefficient.

Factor	DF	SS	MS	% C	% C’	F
temperature	2	1.42	0.71	8.25%	7.54%	8.1
speed	2	0.02	0.01	0.11%	-	(0.11)
compression	2	0.33	0.17	1.92%	-	(1.89)
lubricant	2	15.53	7.77	89.72%	92.46%	88.1
error	0	-	-	-	-	-
(error)	(4)	(0.35)	(0.09)	-	-	-
sum	8	17.31	8.66	100%	100%	-

.

Since the factors with low variance could be considered random background noise, their SS and MS could then be pooled to error. Speed and compression have been determined to be part of the random background noise, as their contributions are as low as 0.11% and 1.92%, respectively. The resulting error calculation is as shown in the extra row with brackets in Table 5. Based on this pooling, it can be further noted that the contribution % C’ of the lubricant is 92.46% and the working temperature has only 7.54% of contribution, approximately 12:1, which is not 3:1 as described in the response table.

If the null hypothesis that there is no significant difference of the variance caused by the working temperature from errors is to be rejected, the F value required for the 95% confidence level is 6.94. The F value calculated from Table 5 (ratio of MS’s from factor and error) exceeds the critical value. It means that the variation caused by the working temperature is significantly different to the random background. The variation caused by speed and compression could still be regarded as random variation or error, because their F values shown in parentheses are relative small in regard to the critical value 6.94, which means that there is no significant difference to the random background noise.

In addition, it can be seen that the impact of the friction coefficient is indeed only the lubricant in this study. Thus the lubricants assigned in this study could accurately describe the frictional boundary condition for the study of grain size.

3.2. Grain Size after Compression Test

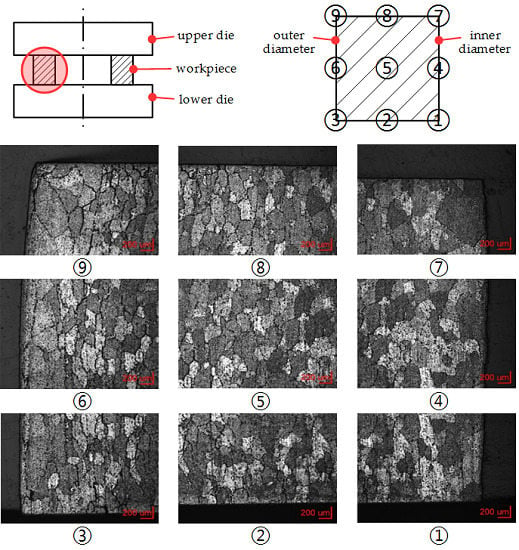
The grain sizes measured from the ring compression test are shown in

Table 6. Average grain size measured from each experiment and each sampling position (unit: μm).

Experiment No.	Position									Mean	Standard Deviation
	1	2	3	4	5	6	7	8	9
1	214	226	233	206	219	258 1	206	219	317 1	233	35
2	233	223	237	207	204	216	230	204	219	219	13
3	233	223	223	194	204	201	201	194	194	207	15
4	237	199	215	188	188	215	244 1	193	222	211	21
5	251 1	251 1	251 1	215	215	215	215	251 1	229	233	18
6	251 1	244 1	244 1	210	193	215	251 1	201	222	226	22
7	237	229	251 1	222	215	244 1	251 1	215	237	233	14
8	251 1	215	251 1	215	215	215	229	215	251 1	229	17
9	261 1	229	290 1	222	251 1	244 1	251 1	215	251 1	246 1	23
mean	241 1	227	244 1	209	212	225	231	212	238	226	13
std. deviation	14	15	22	12	18	19	20	18	34	N/A	N/A

¹ Grain size larger than that from the incoming alloy.

. The positions shown in Table 6 are defined in Figure 5. The sampling positions 1 to 3 are assigned to the region where the specimen contacts to the lower die, while positions 7 to 9 are assigned to the upper die. The sampling positions 4 to 6 are located in the middle part of the specimen without any contact to either to the upper die or to the lower die. The grain sizes shown in Table 6 are the average from the readings of five specimens tested under the same setting. The grain sizes shown with a footer 1 in Table 6 are larger than that measured from the incoming alloy.

Although Figure 5 shows that the positions where the specimen contacts the upper and lower die should be vertically symmetrical and their grain sizes should be comparably similar, the results shown in Table 6, however, are quite different. The reason for this is that the specimen is placed on the lower die first and then contacts to the upper die, so that positions 1 to 3 are early brought into contact with die and therefore cooled. Thus their grain size is different to that on the upper boundary.

Among the mean grain sizes for each experiment setup, it can be observed that the mean grain size was obtained from experiment 3, which reaches the minimum as 207 μm, while experiment 9 can cause the maximum one in 246 μm. Furthermore, only experiment 9 can cause a mean grain size larger than that obtained from the incoming alloy. The remaining experiments only have smaller mean grain sizes. Among those experiments, the grain size in experiment 2 and 3 becomes smaller at all sampling positions. In view of the standard deviation, it can be further seen that experiment 1 has the largest standard deviation, 35 μm, which means that the sampling position in this case might significantly influence grain size. On the other hand, the standard deviation in experiment 2 is the smallest, only 13 μm, suggesting that this experiment setup might cause a relatively homogeneous distribution of grain size.

If the grain size is observed at individual position, the grains at position 9 from experiment 1 are the coarsest, 317 μm in average, while position 4 and 5 from experiment 4 have the smallest grain size, 188 μm in average. Furthermore, position 4 has the smallest mean grain size as well, 209 μm, while position 3 has the largest one, 244 μm. In addition to position 3, position 1 has a mean grain size larger than that from the incoming alloy as well. The remaining positions have grains smaller than that of the incoming alloy. Position 4 of the specimen under all 9 experiment setups has a smaller grain size than that from the incoming alloy. In view of standard deviation of grain size at a certain position obtained under different experiment setups, position 9 has the largest standard deviation of grain sizes, 34 μm, which means that this position might demonstrate the influence of setups designed by Taguchi method, while position 4 shows the smallest one, only 12 μm, which means that at this position the grain size is less sensitive to the settings designed by Taguchi method.

It is still hard to observe the influence of individual level of each factor on the grain size from Table 6. Based on Taguchi method, the grain size at each sampling position is regarded as the quality characteristic value y having the smaller-the-better property. This suggests that the finer the grain, the better the property, so that it can be converted into S/N ratio according to Equation (1). After averaging the S/N ratios for each level of each factor, a response table for each position can be established

Table 7. Response table of factors and their levels on grain size based on S/N ratio (unit: dB) determined by Taguchi method.

Level and Effect of Factor	Position									Mean
	1	2	3	4	5	6	7	8	9
temperature (°C)
400	−47.1 2	−47.0 2	−47.3 2	−46.1 2	−46.4	−47.0	−46.5 2	−46.2 2	−47.5	−46.9 2
450	−47.8	−47.2 3	−47.5	−46.2	−46.0 2	−46.6 2	−47.5	−46.6	−47.0 2	−47.0
500	−47.9 3	−47.0	−48.4 3	−46.9 3	−47.1 3	−47.4 3	−47.7 3	−46.6 3	−47.8 3	−47.5 3
effect	0.84	0.24	1.15	0.73	1.14	0.74	1.21	0.40	0.78	0.61
speed (mm/min)
0.36	−47.2 2	−46.8 2	−47.3 2	−46.2 2	−46.3 2	−47.5 3	−47.3	−46.4	−48.2 3	−47.1
3.6	−47.8	−47.2	−47.8	−46.5 3	−46.5	−46.7 2	−47.0 2	−46.9 3	−47.3	−47.1 3
36	−47.9 3	−47.3 3	−48.0 3	−46.4	−46.6 3	−46.8	−47.4 3	−46.2 2	−46.9 2	−47.1 2
effect	0.70	0.54	0.66	0.30	0.33	0.88	0.32	0.78	1.26	0.02
compression (mm)
1	−47.5 2	−47.2	−47.7	−46.5 3	−46.4 2	−47.2 3	−47.2	−46.5	−48.3 3	−47.3 3
2	−47.7 3	−46.7 2	−47.8 3	−46.3 2	−46.6 3	−47.0	−47.7 3	−46.2 2	−47.3	−47.1
3	−47.6	−47.4 3	−47.6 2	−46.4	−46.5	−46.8 2	−46.9 2	−46.8 3	−46.8 2	−47.0 2
effect	0.21	0.67	0.16	0.21	0.16	0.35	0.75	0.60	1.49	0.22
lubricant
none	−47.7 3	−47.4 3	−48.2 3	−46.6 3	−47.2 3	−47.5 3	−47.0 2	−47.2 3	−48.4 3	−47.6 3
graphite	−47.6 2	−47.3	−47.7	−46.6	−46.2	−47.0	−47.7 3	−46.3	−47.1	−47.1
MoS2	−47.6 2	−46.5 2	−47.2 2	−46.0 2	−46.1 2	−46.5 2	−47.0	−46.0 2	−46.9 2	−46.7 2
effect	0.03	0.91	1.01	0.68	1.04	1.09	0.76	1.11	1.52	0.85

² Level has the largest S/N ratio. ³ Level has the smallest S/N ratio.

. As mentioned above, the larger the effect or the S/N difference among the levels of the same factor, the more significant the influence of the factor on the quality characteristic. From the response listed in the rightmost column of Table 7, which is calculated from the mean grain size in Table 6, it can be observed that the effect of the lubricant on the mean grain size was the most significant (0.86 dB), followed by the working temperature (0.59 dB), and the weakest is then the upsetting speed (only 0.02 dB).

Comparing the S/N ratios responded from each level of each factor, their largest one has a footer of 2, while their smallest one has a footer of 3, to highlight them. It can be seen that the setting with footer 2 in the rightmost column of Table 7 corresponds a working temperature 400 °C with a speed of 36 mm/min and a compression amount of 3 mm with lubricant of molybdenum disulfide. This coincides with the setting of experiment 3 (see Table 2), and provides the smallest mean grain size, which is again consistent with the foregoing description of Table 6. The largest mean grain size would be obtained with a setting with footer 3 as a temperature of 500 °C, a speed of 3.6 mm/min and a compression amount of 1 mm without lubricant. No corresponding set is listed in Table 2, thus experiment 9 with a speed of 36 mm/min and a compression of two millimeters still could be taken as the setting for the largest mean grain size, as the two most significant factor, lubricant (no lubricant) and temperature (500 °C) are already considered. This again is confirmed by the foregoing description of Table 6. Figure 6 shows the microstructure images taken at each sampling position in experiment 1, in which the grains on the top inner corner are coarser.

In addition, it can be seen in Table 7 that the lubricant has a significant effect on the grain size. The setting without lubricant can generate large grains at most (8) positions, while the setting with molybdenum disulfide can generate small grains at most (8) positions. In addition, the working temperature has the second significant effect on the grain size. The setting at 500 °C can let most (8) positions have large grains, while the setting at 400 °C can produce small grains at some (6) positions. The factors with less effect on grain sizes, such as speed and compression amount have no fixed level to the output of large or small grains, which matches that shown in the response table in the rightmost column of Table 7. Regarding the response to the grain size at each position, the most significant factor is again either the working temperature or the lubricant. For positions 1, 3, 4, 5, and 7, the working temperature is the factor with the most significant influence on the grain size at that position, while the lubricant has the impact on the grain size only at positions 2, 6, 8, and 9.

As discussed above, ANOVA is still needed to figure out how strongly the factors affect the quality characteristics in the response tables.

Table 8. Analysis of Variance in grain size.

Factor	DF	SS	MS	% C	% C’	F
temperature	2	0.617	0.3083	34.37%	35.33%	14.8
speed	2	0.001	0.0003	0.03%	-	(0.01)
compression	2	0.083	0.0415	4.62%	-	(1.99)
lubricant	2	1.094	0.5471	60.98%	64.67%	26.2
error	0	-	-	-	-	-
(error)	(4)	(0.083)	(0.0417)	-	-	-
sum	8	1.794	0.8971	100%	100%	-

is the ANOVA for the mean grain size calculated by the method mentioned in Section 3.1. The same measures in Table 5 can be also applied to Table 8, in which the variances from the factors with relatively low variances, such as speed and compression, are pooled to that of error. It further can be pointed out that the contribution % C’ of lubricant is 64.67%, while the working temperature has a 35.33% contribution. The ratio of both them is nearly 2:1, not as described in the response table in Table 7—about 7:5. Regarding to the F test, same as described in the previous section, at a more than 95% confidence level, variations caused by upsetting speed and compression can be regarded as random variation or error.

3.3. Grain Size after T6 Temper

After T6 heat treatment, in which the specimens were solid-solutioned at 530 °C for two hours, then quenched in water, and thereafter artificially aged at 170 °C for eight hours, the grain sizes were measured as listed in

Table 9. Average grain size obtained after T6 temper (unit: μm).

Experiment No.	Position									Mean	Standard Deviation
	1	2	3	4	5	6	7	8	9
1	222	244 1	244 1	215	251 1	300 1	251 1	222	251 1	244 1	25
2	215	205	215	158	135	228	151	177	199	187	33
3	148	150	154	141	135	144	153	150	164	149	8
4	147	153	135	150	150	167	150	164	150	152	9
5	150	125	150	133	127	167	133	125	127	137	15
6	251 1	215	251 1	222	215	244 1	261 1	215	290 1	240 1	26
7	130	147	145	135	135	188	167	138	135	147	19
8	232	215	283 1	244 1	222	300 1	222	251 1	244 1	246 1	29
9	135	153	150	147	138	167	135	164	135	147	12
mean	181	179	192	172	168	212	180	178	188	183	13
std. deviation	48	41	56	43	48	59	50	42	60	N/A	N/A

¹ Grain size larger than that from the incoming alloy.

.

The average grain size was 183 μm, which is smaller than the average value of 226 μm after the compression test. This means that the T6 heat treatment can generally refine the grain size further after compression. Experiment 5 could refine the grain size to 137 μm from 233 μm and achieved 41% refinement. However, there were also a couple of coarsening setups: experiment 1, 6, and 8, among which experiment 8 had an average grain size of 246 μm and a coarsening of 8% from 229 μm. In view of the standard deviation, the grain sizes in sampling positions formed by experiment 2 were significantly different and had a standard deviation of 33 μm, while the standard deviation of the grain size in the positions formed by experiment 3 is only 8 μm. It seems that it is difficult to distinguish the differences between the positions formed by experiment 3. In fact, a similar situation could be found in experiments 4 and 9, in which the standard deviations were only 9 μm and 12 μm. With regard to the average grain size calculated for each sampling position, the mostly refined grains from compression to aging were found in position 1, in which a 25% refinement from 241 μm to 181 μm could be achieved. Even in the worst case, such as the grain size in position 6, there was still 6% refinement achieved by aging. However, the standard deviation of the grain size there among the experiments was 59 μm, which means that there was a significant difference among the experiment setups.

From the mean S/N ratio listed in the rightmost column of

Table 10. Response table of factors and their levels on grain size obtained after T6 temper (unit: dB).

Level and Effect of Factor	Position									Mean
	1	2	3	4	5	6	7	8	9
temperature (°C)
400	−45.7 3	−45.9 3	−46.1 3	−44.7 3	−44.4 3	−46.7 3	−45.2 3	−45.2 3	−46.1 3	−45.6 3
450	−45.0	−44.1 2	−44.7 2	−44.3 2	−44.1 2	−45.6 2	−44.8	−44.3 2	−45.0	−44.7 2
500	−44.1 2	−44.6	−45.3	−44.6	−44.1	−46.5	−44.7 2	−45.0	−44.3 2	−44.9
effect	1.58	1.75	1.36	0.34	0.32	1.13	0.49	0.87	1.80	0.94
speed (mm/min)
0.36	−44.2 2	−44.9	−44.5 2	−44.3 2	−44.7 3	−46.5	−45.3 3	−44.7 2	−44.7 2	−44.9
3.6	−45.9 3	−45.0 3	−46.4 3	−44.9 3	−43.9 2	−47.1 3	−44.4 2	−45.0 3	−45.3	−45.4 3
36	−44.7	−44.6 2	−45.1	−44.4	−44.0	−45.1 2	−44.9	−44.8	−45.4 3	−44.8 2
effect	1.65	0.33	1.89	0.60	0.83	1.98	0.92	0.29	0.68	0.60
compression (mm)
1	−47.4 3	−47.0 3	−48.3 3	−47.1 3	−47.2 3	−48.9 3	−47.8 3	−47.2 3	−48.3 3	−47.8 3
2	−44.2	−44.6	−44.3	−43.7	−43.0	−45.4	−43.3 2	−44.5	−44.1	−44.2
3	−43.1 2	−42.9 2	−43.5 2	−42.7 2	−42.4 2	−44.4 2	−43.6	−42.8 2	−43.0 2	−43.2 2
effect	4.36	4.08	4.76	4.42	4.77	4.57	4.47	4.44	5.35	4.56
lubricant
none	−44.4 2	−44.5 2	−44.9 2	−44.2 2	−44.3	−46.2	−44.4 2	−44.4 2	−44.2 2	−44.7 2
graphite	−45.6 3	−45.4 3	−46.0 3	−44.6	−44.0 2	−46.9 3	−45.5 3	−44.8	−46.0 3	−45.6 3
MoS2	−44.7	−44.6	−45.2	−44.8 3	−44.4 3	−45.7 2	−44.7	−45.3 3	−45.2	−45.0
effect	1.29	0.96	1.03	0.60	0.41	1.13	1.16	0.87	1.76	0.91

² Level has the largest S/N ratio. ³ Level has the smallest S/N ratio.

, the smallest grain size might be achieved according to Taguchi method by setting the level of each factor, which had the largest S/N ratio, namely, the operating temperature at 450 °C, the speed at 36 mm/min, the compression at three millimeters and no lubricant used. However, no such experiment setup listed in Table 2 could be found. Nevertheless, experiment 5 has the most similar setup, which had just one alternation in speed, 3.6 mm/min instead of 36 mm/min (Table 2), and whose response shown in Table 9 really had the smallest among the nine experiment setups.

Similarly, the largest grain size might be accordingly achieved by setting temperature at 400 °C, speed at 3.6 mm/min, compression at one millimeter and with lubricant of graphite. The most comparable settings fall onto experiment 2, which only changes the compression at two millimeters (see Table 2). However, this setting could not achieve the largest grain size as described in Table 9. If temperature were changed to 500 °C and the lubricant to molybdenum disulfide as in the setting in experiment 8, or speed to 0.36 mm/min without lubricant as in experiment 1, or temperature to 450 °C and speed to 36 mm/min as in experiment 6, a larger grain could be achieved than by experiment 2. Among these experiments, the very same setting is the compression at one millimeter. This fact could also be found from the result not only in the rightmost column but also in the column of each individual position listed in Table 10. The most significant effect on the grain size is the compression, and its level at one millimeter has the lowest S/N ratio as well, while three millimeters has the highest S/N ratio (in 8 of all 9 positions). Furthermore, the second significant effect on the grain size is the temperature, in which 400 °C had a strong tendency (lowest in mean S/N ratio and all 9 positions) to have coarse grain, while 450 °C relatively easily (highest in mean S/N ration and only six positions) causes fine grain. Within the factors, lubricant and speed, their levels having larger or smaller grain, are very irregular among individual positions and therefore they had less effect on grain size.

Resulting from the ANOVA,

Table 11. Analysis of variance in grain size obtained after T6 Temper.

Factor	DF	SS	MS	% C	% C’	F
temperature	2	1.48	0.74	3.91%	-	(1.32)
speed	2	0.63	0.31	1.65%	-	(0.56)
compression	2	34.56	17.28	91.13%	100%	30.8
lubricant	2	1.26	0.63	3.32%	-	(1.12)
error	0	-	-	-	-	-
(error)	(6)	(3.37)	(1.68)	-	-	-
sum	8	37.93	18.96	100%	100%	-

shows that factors mentioned above with relative low difference of S/N ratio, such as temperature, lubricant, and speed, have also a low contribution (%C). The variation caused by them can then be regarded as random background and can be pooled to error, which is correct in view of F value, because their F values are relatively small when compared to the critical value 6.94. Thus, only compression is the remaining factor to grain sizes after T6 temper.

It can be seen that T6 temper could further make grains finer and this refinement has an absolute relationship to the amount of compression. This can be attributed to the fact that at elevated temperature, severe ongoing plastic deformation beyond the critical strain can cause recrystallization, which is called dynamic recrystallization. If the plastic deformation is terminated, the larger retaining plastic strain will undergo further metadynamic recrystallization, while the smaller retaining plastic strain will undergo static recrystallization. These three recrystallizations will refine the grains. In the meantime, at such elevated temperatures, grain growth coarsens the grains to reduce their number and to release the grain surface energy as well as to lower the free energy [10]. Usually, the hot forging process takes place within a relatively short span of time, frequently less than one second. The dynamic recrystallization can be just initiated and take place in a short duration. Furthermore, some of the experiments had relative small amount of compression, which might restrict the initiation of dynamic recrystallization during the compression test. This caused the grain refinement to not be efficient. The subsequent heat treatments, such as solid solution (two hours) and aging (eight hours), had sufficient time for grains to have full recrystallization either by metadynamic recrystallization or by static recrystallization, so that finer grains could be obtained. Additionally, experiments 1, 6, and 8, which had small amounts of compression, had relatively coarse grains, which was due to their small plastic deformation amount. At the same time, grain growth still occurred and made grains coarser.

4. Conclusions

This study used a ring compression test with working temperature, upsetting speed, compression amount, and lubricant as process parameters. Each of the factors had three levels to form an orthogonal experiment table of L9 according to the Taguchi method to analyze the grain size after hot forging a 6061 aluminum alloy and after T6 temper. The surface layers of the specimen were peeled in order to eliminate the peripheral coarse grains from the previous processes used in preparing the billet.

As a result, no peripheral coarse grains were found in any of the specimens, which were peeled and compressed. However, the relative significance of each factor still can be found by Taguchi analysis with ranking the process factors according to their influence on the mean grain size of each experiment. It is determined that the most significant factor is the lubricant, followed by the working temperature and then by the amount of compression, and the upsetting speed was negligible. In view of the two most significant factors, lubricant and working temperature, the usage of molybdenum disulfide can achieve smaller grains, while applying no lubricant can easily cause grain coarsening, and a higher working temperature of 500 °C can steadily conduct grain coarsening as well. Regarding the impact of each of these two factors to the grain size at each sampling position, the above conclusions are still applicable. The results from experiments in the ring compression test showed that the minimum mean grain size was 207 μm and the maximum was 246 μm, which could not be easily distinguished from that measured from the incoming alloy, 237 μm. It is apparent that the effect of grain coarsening or grain refinement per hot forging is not recognizable. This can be attributed to the fact that the processing duration of forging operation is too short, so that the dynamic recrystallization and grain growth could not take place in the microstructure adequately.

On the other hand, the compression tested aluminum alloys could have finer mean grain size after solid solution and artificial aging T6 temper. According to the Taguchi method and ANOVA, the only process factor in compression test that significantly influences the grain size after T6 temper is the compression amount. The greater the compression, the smaller the grain size achieved. A slight compression can cause grain sizes to be larger than both those of the incoming alloy and those just after compression test. The heating at elevated temperature during T6 temper can let the relatively strained alloy during compression test further undergo metadynamic or static recrystallization, so that the grain size is steadily smaller.

In addition, this study also proved that only lubricants significantly affect the friction coefficient in a ring compression test of a 6061 aluminum alloy. The effect of working temperature on the friction coefficient is still relatively low.