Low-Voltage Ride-Through Control Strategy for a Grid-Connected Energy Storage System

Abstract

This paper presents a low-voltage ride-through (LVRT) control strategy for grid-connected energy storage systems (ESSs). In the past, researchers have investigated the LVRT control strategies to apply them to wind power generation (WPG) and solar energy generation (SEG) systems. Regardless of the energy source, the main purpose of the LVRT control strategies is to inject reactive power into the grid depending on the grid-code regulations using the grid-side inverter; the proposed LVRT control strategy for grid-connected ESSs also has the same purpose. However, unlike the WPG and SEG systems having unidirectional power flow, grid-connected ESSs have a bidirectional power flow. Therefore, the charging condition of the grid-connected ESSs should be considered for the LVRT control strategy. The proposed LVRT control strategy for grid-connected ESSs determines the injection quantity of the active and reactive currents, and the strategy depends on the voltage drop ratio of the three-phase grid. Additionally, in this paper, we analyzed the variations of the point of common coupling (PCC) voltage depending on the phase of the reactive current during the charging and discharging conditions. The validity of the proposed LVRT control strategy is verified and the variations of the PCC voltage of the grid-connected ESS are analyzed by simulation and experimental results.

1. Introduction

In recent years, the depletion of fossil fuels and environmental pollution have become important matters of global concern because they cause the depletion of energy resources and global warming. Accordingly, the demand for the use of renewable energy sources, such as wind power, solar energy, and biomass, has rapidly increased [1,2,3]. To meet the demand and reduce the problems associated with the depletion of fossil fuels and environmental pollution, numerous studies have been conducted for green energy and renewable energy development [4,5,6]. The common renewable energy systems are wind power generation (WPG), which uses wind turbines, and solar energy generation (SEG), which uses photovoltaic cells. However, sources such as wind power and solar energy might be unreliable and unpredictable because of changes in environmental conditions. Therefore, energy storage systems (ESSs) are used for conserving energy generated by the renewable energy sources in battery systems.

The grid-connected ESS usually generates and supplies power by connecting to a grid. It is used for conserving the additional energy with a reasonable cost, such as at night. Moreover, it can improve the energy quality and maximize its efficiency by supplying the conserved energy on requirement. The ESS has been made commercially available as typical renewable energy and energy conservation systems [7,8,9,10,11].

Power generation systems connected to the grid can have a negative impact on the grid in case the power scale of the systems becomes large. Therefore, several countries suggest grid-code regulations to mitigate the negative impacts on the grid. Grid-code regulations differ from country to country; Germany’s grid-code regulations are more rigorous than the grid-code regulations of other countries. In general, the grid-code regulations define that systems such as WPG and SEG have to remain connected to the grid when the voltage drops for a specified time and support the grid with a reactive current. This requirement, known as a low-voltage ride-through (LVRT), is needed to avoid grid blackouts.

The LVRT requirement is crucial for grid-code regulations. Figure 1 shows the LVRT requirements in Germany and China. The requirements are different regarding a fault duration and the injection quantity of the reactive power depending on the voltage drop ratio. This requirement ensures that the system connected to the grid operates properly when the grid voltage drops [12,13,14,15,16,17,18]. The LVRT requirement contributes to the recovery of the grid voltage by supplying the reactive current in the designated voltage range. In order to satisfy the LVRT requirement, a proper control of the reactive current in the grid-connected ESS is necessary. To control the reactive power and the current for the grid-connected inverters in the WPG, SEG, and ESS is crucial. Numerous studies have been conducted for issues related to the reactive power and current compensation capabilities of such systems [19,20,21,22,23,24,25].

The WPG systems using wind turbines and the SEG systems using photovoltaic cells usually have a large power scale. Therefore, the LVRT requirement needs to be thoroughly implemented in these systems. The LVRT control strategies researched recently comply with the LVRT requirement. In addition, these strategies focus on the additional operations that are effective and economical, which include the continuously stable operations with dynamic breakers in the WPG systems [26,27,28,29,30] and the maximum power generation with low voltages in the SEG systems [31,32,33]. These methods for additional operations are presented by considering the characteristics of the source type. The research on the LVRT control strategies for the WPG and SEG systems is actively progressed, however, the research on the LVRT control strategy for the grid-connected ESSs is insufficient.

The WPG and SEG systems are characterized by unidirectional power flow, which are unlike the grid-connected ESSs that are characterized by bidirectional power flow. Therefore, the LVRT control strategy used for the grid-connected ESSs needs to comply with the LVRT requirement, additionally, the characteristics of bidirectional power flow, i.e., the charging conditions of the grid-connected ESSs, need to be considered in the LVRT control strategy. The LVRT control strategy for the ESS is presented in [34]. In [34], when the grid voltage drops under charging condition of the grid-connected ESS, the LVRT control strategy is applied after the condition of the grid-connected ESS is changed to the discharging condition. It contributes to increase the voltage at the point of common coupling (PCC). This LVRT control strategy can be applied in applications improving the grid voltage durability such as frequency regulator that improves the grid frequency stability [35], [36]. However, in applications with other system connected to the DC-link of the grid-connected ESS, the charging condition of the grid-connected ESS must be maintained although the grid voltage drops. This paper presents the LVRT control strategy for grid-connected ESSs by considering the characteristic of bidirectional power flow. The proposed LVRT control strategy complies with the LVRT requirement and operates for contributing to increase voltage at the PCC. In other words, when the grid voltage drops, the proposed LVRT control strategy determines the injection quantity of the active and reactive currents depending on the voltage drop ratio of the three-phase grid. Additionally, in this paper, we analyzed the variations of the PCC voltage depending on the phase of the reactive current of the grid-connected ESS during the charging and discharging conditions. The validity of the proposed LVRT control strategy is verified and the variations of the PCC voltage of the grid-connected ESS are analyzed by PSIM simulation and experimental results.

2. LVRT Control Strategy for Renewable Energy Systems

2.1. LVRT Control Strategy in the WPG System

Figure 2 shows the configuration of the WPG system that uses a back-to-back converter. This system comprise a generator connected to a blade, a back-to-back converter (with a dynamic breaker), a filter, a transformer, and a three-phase grid. The generator with the blade has a large inertia; therefore, the WPG system cannot instantaneously reduce the power. The back-to-back converter is the representative topology used in WPG systems, and it comprises a generator-side converter, DC-link with a dynamic breaker, and grid-side inverter.

When the grid voltage drops in the WPG system, the power limited by the rating current is reduced because of the low grid voltage. Therefore, surplus power exists, and it considerably increases the DC-link voltage. If the WPG system decreases the power generation for preventing the production of surplus power, the blade speed increases owing to the large inertia of the generator with the blade. Finally, the increase in the blade speed or the DC-link voltage can lead to the destruction of the WPG system. Therefore, when the grid has a low voltage, the LVRT control strategies for the WPG system should focus on the stable operation of the WPG system. In the WPG system, another device is required to consume the surplus power, comply with the LVRT requirement, and maintain stable operation. Therefore, a dynamic breaker is included in the back-to-back converter; the dynamic breaker, called crow bar, comprises a resistor and a switch.

The LVRT control strategies for the WPG system under low grid voltage determine the injection quantity of the reactive current (I_de) by the LVRT requirement depending on the level of low voltage. In addition, the active current (I_qe) for transferring the active power allowed in the range of the rating current (I_rating) of the WPG system is calculated as in (1).

$$I_{qe}=\sqrt{I_{rating}^2-I_{de}^2}$$

(1)

where I_de and I_qe, which represent the reactive and active powers, respectively, are the d-q axis currents in the synchronous reference frame. These are reflected in the control of the grid-side inverter. If surplus power is generated, the generator-side converter is able to reduce the power until the blade speed becomes equal to the rating speed. At the rating speed of the blade, the dynamic breaker operates to decrease the DC-link voltage.

2.2. LVRT Control Strategy in the SEG System

Figure 3 shows the configurations of the SEG systems, which are typically classified into two topologies: the one-state topology without a DC/DC converter (see Figure 3a) and the two-stage topology with a DC/DC converter (see Figure 3b). The SEG system comprises photovoltaic (PV) arrays, a power conversion system (comprising a DC/DC converter and a grid-side inverter), a filter, and a three-phase grid.

If the grid voltage drops in the SEG system, regardless of the topology, reactive power is injected in the grid-side inverter to comply with the LVRT requirement, which is similar to the case of WPG system. However, the LVRT control strategies for the SEG systems are different from those for the WPG systems. In the SEG system, the LVRT control strategy with maximum power generation is widely used. Using the LVRT control strategy, the d-axis current (I_de) required for injecting the reactive power into the grid having a low voltage is determined based on the LVRT requirement depending on the level of low voltage. In addition, to transfer the maximum power from the PV arrays to the grid with low voltage, the active current is calculated by (1). Unlike the LVRT control strategy for the WPG systems, in the SEG systems, the LVRT control strategy focuses on the power generation.

In Figure 3b, the DC/DC converter transfers the input power corresponding to the output power calculated using I_qe and the low grid voltage.

3. Proposed LVRT Control Strategy for Grid-Connected ESSs and Analysis of PCC Voltage Variation

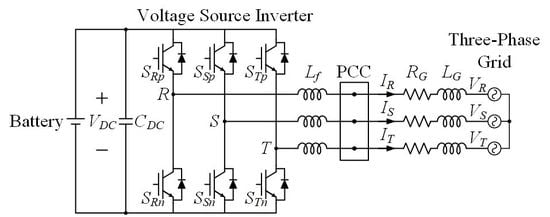
Figure 4 shows the circuit configurations of the grid-connected ESS using a voltage source inverter (VSI). It comprises a battery, DC-link capacitors (C_DC), a VSI, a filter (L_f), the resistive impedance (R_G) and inductive impedance (L_G) elements of the grid, and a three-phase grid. The VSI comprises six insulated gate bipolar transistors (IGBTs) with antiparallel diodes. In addition, there is a PCC between the filter and the three-phase grid. The three-phase grid generates balanced three-phase grid voltages (V_R, V_S, and V_T) having constant frequencies.

3.1. Proposed LVRT Control Strategy for a Grid-Connected ESS

The LVRT control strategy needs to be applied in the grid-connected ESS having a large power scale. This strategy generally considers the characteristic of the source type or the application of the system. However, regardless of the characteristics or application, the main purpose of the LVRT control strategy is to comply with the LVRT requirement and inject reactive power through the grid-side inverter on the basis of the gird-code regulations.

The characteristics of the grid-connected ESS are different from those of the WPG and SEG systems; the grid-connected ESS with the battery in the DC-link has bidirectional power flow depending on the charging and discharging conditions, unlike the WPG and SEG systems, which have unidirectional power flow. Therefore, the LVRT control strategy for the grid-connected ESS needs to consider the charging and discharging conditions.

When the grid voltage drops during ESS operation under the discharging and charging conditions, the proposed LVRT control strategy for the grid-connected ESS becomes similar to the strategy for the WPG and SEG systems. The proposed LVRT control strategy determines the injection quantity of the reactive current for injecting reactive power into the three-phase grid depending on the grid-code regulation. In addition, the active current for transferring active power is determined within the range of the rating current of the grid-connected ESS.

The method for determining the injection quantity of the active and reactive currents depends on the voltage drop ratio of the three-phase grid as shown in Figure 5. The voltage-level (V_LEVEL) of the three-phase grid is calculated by the voltage-level calculation process using the three-phase grid voltages V_R, V_S and V_T. V_LEVEL is classified into three parts depending on the LVRT requirement of the grid-code regulations, and the method for determining the injection quantity of the active and reactive currents is selected by each part. If V_LEVEL is greater than 90% of the three-phase grid voltage under normal conditions, the reactive current injected into the three-phase grid is zero, and the active current becomes the reference current. If V_LEVEL is greater than 50% but less than 90% of the three-phase grid voltage, then reactive current to be injected into the three-phase grid is determined based on the voltage drop ratio of the three-phase grid. In addition, the active current is calculated using the reactive current and the rating current of the grid-connected ESS. If V_LEVEL is less than 50% of the three-phase grid voltage, the reactive current injected into the three-phase grid is the rating current of the grid-connected ESS, and the active current is zero.

Figure 6 shows the voltage-level calculation process using V_R, V_S and V_T as the three-phase grid voltages. The voltage magnitudes (V_R(mag), V_S(mag) and V_T(mag)) of each phase in the three-phase grid is calculated by V_R, V_S and, V_T and the three-phase grid voltages (V_R(shift), V_S(shift) and V_T(shift)), which are transformed by the orthogonal signal generator such as the all-pass filter. In addition, V_LEVEL is determined by V_R(mag), V_S(mag), and V_T(mag) using the maximum value estimation. The V_LEVEL obtained by the voltage-level calculation process that uses the three-phase grid voltage magnitude is important because it is used for detecting the LVRT requirement.

As a result, the proposed LVRT control strategy for a grid-connected ESS determines the injection quantity of the active and reactive currents depending on the voltage drop ratio of the three-phase grid, which is based on the grid-code regulation.

Figure 7 shows the control block diagram of the grid-connected ESS with the proposed LVRT control strategy. The V_R, V_S and V_T are used to detect the phase angle of the three-phase grid using the phase-locked loop (PLL). Additionally, they are used for the voltage-level calculation process, which determines V_LEVEL. Using V_LEVEL and the LVRT control strategy, the active and reactive reference currents are determined.

3.2. Analysis of PCC Voltage Variation

When the ESS operates under the discharging condition, the active current is injected into the three-phase grid from the ESS. In this case, the PCC voltages are changed by the phase of the reactive current injected into the three-phase grid. Figure 8 shows the variations of the PCC voltage in the discharging condition of the ESS depending on the phase of the reactive current. V_G is the grid voltage, and I_G is the grid current flowing between the ESS and the three-phase grid. In this paper, when I_G is positive, it flows to the three-phase grid from the ESS. The d-axis refers to the reactive component, and the q-axis refers to the active component. V_PCC is the PCC voltage, which is the sum of V_G and the voltage drops (V_RG and V_LG) of the resistor–inductor of the three-phase grid. In Figure 8a, I_G includes only the active current, which means that the reactive current is zero. V_PCC is occurred by V_G, V_RG, and V_LG, and it has a phase equal to that of I_G. When the inductive or capacitive reactive current is injected into the three-phase grid, V_PCC is changed by the variation of the phases of V_RG and V_LG, as shown in Figure 8b,c. In other words, V_PCC decreases because of the injection of the inductive reactive current, and it increases because of the injection of the capacitive reactive current. As a result, in the discharging condition of the ESS, the active current with the capacitive reactive current injected into the three-phase grid contributes to an increase of V_PCC and meets the LVRT requirement.

When the ESS operates under the charging condition, contrary to the discharging condition, the active current flows to the ESS from the three-phase grid. V_PCC is also changed by the phase of the reactive current flowing to the ESS. The variations of V_PCC in the charging condition of the ESS depending on the phase of the reactive current is shown in Figure 9. In Figure 9a, I_G includes only the active current without the reactive current. It does not contribute to the increase of V_PCC because I_G has a negative direction. In Figure 9b,c, V_PCC is changed by the injection of the inductive and capacitive reactive currents, respectively. V_PCC decreases when the inductive reactive current is injected, and it increases when the capacitive reactive current is injected. Therefore, in the charging condition of the ESS, the active current with the capacitive reactive current contributes to the LVRT requirement.

When the grid voltage drops in the grid-connected ESS, the proposed LVRT control strategy is required to comply with the LVRT requirement. The proposed LVRT control strategy determines the injection quantity of the active and reactive currents, and the strategy depends on the voltage drop ratio of the three-phase grid. In addition, regardless of the operating condition of the ESS, such as the charging and discharging conditions, the injection of the capacitive reactive current contributes to the LVRT requirement because of the increase of V_PCC. The validity of the proposed LVRT control strategy is demonstrated and the variations of the PCC voltage of the grid-connected ESS are analyzed by simulation and experimental results.

3.3. LVRT Control Strategy Depending on State of Charge of Battery

Contrary to the LVRT control strategy for the WPG and the SEG systems, in the grid-connected ESSs with a battery in the DC-source, shown in Figure 4, a state of charge (SOC) should be considered for the LVRT control strategy. The SOC is an essential indicator used to regulate the operating decisions and to avoid the over-charge or over-discharge. However, it cannot be measured directly by sensors. In general, the SOC is obtained by the battery management system or various algorithms for estimation of the SOC using the battery model [37,38,39].

In case the SOC is higher or lower than the designated value under the discharging or charging conditions of the grid-connected ESS, the proposed LVRT control strategy, which is mentioned above can be applied. However, in case the SOC is lower or higher than the designated value under the discharging or charging conditions of the grid-connected ESS, the SOC should be considered in the grid-connected ESS with the LVRT control strategy. In other words, if the SOC is lower than the designated value under discharging conditions of the grid-connected ESS, the active current cannot be supplied to the three-phase grid. The other way, if the SOC is higher than designated value under charging conditions, the active current is not required. Therefore, regardless of the grid voltage drops, the grid-connected ESS controls the reactive current as rating current.

4. Simulation Results

To verify the performance of the proposed LVRT control strategy and analyze the variations of the PCC voltage, a simulation that uses the grid-connected ESS as shown in Figure 4 was conducted using the PSIM software. The simulation parameters are listed in

Table 1. Simulation parameters.

Parameters	Value	Unit
DC-link voltage (VDC)	600	V
DC-link capacitor (CDC)	2200	μF
Three-phase grid line-to-line voltage (VG)	380	Vrms
Three-phase grid frequency (fG)	60	Hz
Filter inductance (Lf)	3	mH
Resistive impedance of grid (RG)	0.05	Ω
Inductive impedance of grid (LG)	0.04	mH
Rating power (Prating)	5	kW
Rating current (Irating)	10.7	Apeak
Switching frequency (fsw)	10	kHz

. DC-link voltage (V_DC) generated by the battery was 600 V, and the three-phase grid line-to-line voltage (V_G) was 60 Hz/380 V_rms. In addition, L_f was 3 mH and R_G and L_G were 0.05 Ω and 0.04 mH, respectively.

Figure 10 shows the simulation results of the voltage-level calculation process (given in Figure 6) that uses the three-phase grid voltages V_R, V_S, and V_T. Under normal conditions, V_R, V_S, and V_T are 60 Hz/310 V_peak. However, in Figure 10a, the grid voltage drops, and the magnitudes of V_R, V_S, and V_T decrease to 80%, 60%, and 40%, respectively, of the magnitudes of the phase voltages under normal conditions for intervals ranging from 0.1 to 0.5 s. After that, the magnitudes increase to 70% and 100% as compared with the magnitudes of the phase voltages under normal conditions. The magnitude (V_mag) of V_R, V_S, and V_T is precisely calculated using the voltage-level calculation process as shown in Figure 6. Moreover, V_LEVEL as the voltage-level of the three-phase grid is determined depending on V_mag (as shown in Figure 10b), and V_LEVEL is used for the detecting the LVRT requirement.

Similar to the scenario in Figure 10, Figure 11 shows the simulation results of the proposed LVRT control strategy depending on the detecting the LVRT requirement based on the voltage-level. Figure 11a shows V_LEVEL of the three-phase grid when the voltage drops (as in Figure 10). Figure 11b,c show the d-axis and q-axis currents (I_de and I_qe) and the reference currents (I*_de and I*_qe) of the synchronous reference frame. I_de and I_qe stand for the reactive and the active currents in the synchronous reference frame, respectively. I*_de and I*_qe are determined by the proposed LVRT control strategy depending on the detecting the LVRT requirement using V_LEVEL. In other words, the injection quantity of the active and reactive currents is determined from the voltage drop ratio of the three-phase grid using the method as shown in Figure 5.

If V_LEVEL is 80% during the interval from 0.2 to 0.3 s in Figure 11a, I*_de as the injection quantity of the reactive current is determined to 40% (approximately 4.28 A) of I_rating in the grid-connected ESS as shown in Figure 11b. In addition, if V_LEVEL is lower than 50% during the interval from 0.4 to 0.5 s in Figure 11a, I*_de is determined to 100% (approximately 10.7 A) of I_rating in the grid-connected ESS as shown in Figure 11b. After determining I*_de using the proposed LVRT control strategy, I*_qe as the injection quantity of the active current is calculated using I*_de and I_rating.

As a result, although the grid voltage drops, I_de and I_qe are controlled by I*_de and I*_qe, respectively, using the proposed LVRT control strategy. The proposed LVRT control strategy complies with the LVRT requirement, and the three-phase grid currents (I_R, I_S, and I_T) maintain a sinusoidal waveform, as shown in Figure 11d.

In this paper, an additional simulation was performed to analyze the variations of the PCC voltage depending on the phase of the reactive current injected into the three-phase grid. Figure 12 and Figure 13 show the simulation results of the PCC voltage depending on the phase of the reactive current when the ESS operates under the discharging and charging conditions, respectively. In Figure 12 and Figure 13, the magnitudes of V_R, V_S, and V_T are decreased to 60% as compared with those of phase voltages under normal conditions. Therefore, I*_de was determined to 80% (approximately 8.56 A) of I_rating in the grid-connected ESS through the proposed LVRT control strategy. I*_qe as the reference active current is calculated according to (1) as approximately 6.42 A. The I_qe values as shown in Figure 12c and Figure 13c are controlled by I*_qe (6.42 A in Figure 12c and −6.42 A in Figure 13c), depending on the operating conditions of the ESS, such as the discharging and charging conditions.

As shown in Figure 12b and Figure 13b, the inductive reactive current is injected into the three-phase grid during the interval from 0.3 to 0.5 s, and the capacitive reactive current is injected during the interval from 0.5 to 0.7 s. Depending on the phase of the reactive current injected into the three-phase grid, the PCC voltage (V_PCC) is changed as shown in Figure 12a and Figure 13a with an extended simulation waveform. Regardless of the operating conditions of the ESS, the V_PCC magnitude is higher when the capacitive reactive current is injected as compared with the V_PCC magnitude when the inductive reactive current is injected. Therefore, when the grid voltage drops, the capacitive reactive current determined by the proposed LVRT control strategy needs to be injected into the three-phase grid. This contributes to the PCC voltage increase. The three-phase grid currents (I_R, I_S, and I_T) are shown in Figure 12d and Figure 13d.

Figure 14 and Figure 15 show the simulation results of the active and reactive currents of the grid-connected ESS depending on the SOC under discharging and charging conditions. In the discharging and charging conditions of the grid-connected ESS, the proposed LVRT control strategy is applied when the grid voltage drops. However, in Figure 14, the SOC of the battery in the DC-link is changed from 20 to 10 at 0.3 s. It is lower than designated value, which is decided to 15. Additionally, in Figure 15, the SOC of the battery is changed from 80 to 90 at 0.3 s. It is higher than designated value, which is decided to 85. Fundamentally, the SOC of the battery cannot change as immediately as a step function because it is a dynamic variable. However, it was simulated to show the performance of the proposed algorithm depending on the SOC of the battery. In these cases, regardless of the grid voltage drops, the grid-connected ESS controls the reactive current as rating current.

5. Experiment Results

To verify the validity of the proposed LVRT control strategy and analyze the variations of the PCC voltage, experiments were performed using the experimental setup as shown in Figure 16. In the experimental setup, the DC power supply (TC.GSS.20.600.4WR.S) that has characteristic of the bidirectional power flow is used for the battery as shown in Figure 4. The experimental setup comprised a DC-link, control board, relay, switched mode power supply (SMPS), fan, power board, and magnetic contactor. The SMPS supplies the power to operate the control board and power board. The control board comprised a digital signal processor that used TMS320F28335, and the power board consisted of an inverter stage using the IGBTs and gate drivers. The parameters of the experiment were equal to those of the simulation listed in Table 1.

Figure 17 shows the experimental results of the voltage-level calculation process. Under normal conditions, V_R as the R-phase grid voltage is 60 Hz/310 V_peak. However, in Figure 17, the grid voltage drops. The V_R magnitude decreases from 100% to 80% and further to 60% and 40%; subsequently, it increased to 70% and 100% as compared with the phase voltage magnitude under normal conditions. V_mag as the magnitude of the three-phase grid voltages is precisely calculated. In addition, V_LEVEL is determined, and it was used for detecting the LVRT requirement.

In a scenario similar to that shown in Figure 17, the experimental results of the proposed LVRT control strategy depending on the detecting the LVRT requirement are shown in Figure 18. In Figure 18, I_de and I_qe, which are the reactive and active currents, respectively, are changed by the detecting the LVRT requirement using V_LEVEL and the proposed LVRT control strategy. When V_LEVEL is 80%, I_de is injected into the three-phase grid with 40% of I_rating as the rating current in the grid-connected ESS. If V_LEVEL is lower than 50%, I_de is determined to 100% of I_rating. In addition, I_qe is determined by I_de and I_rating after determining I_de using the proposed LVRT control strategy. As a result, when the grid voltage drops, the proposed LVRT control strategy complies with the LVRT requirement, and I_R as the R-phase grid current is maintained in a sinusoidal waveform, as shown in Figure 18.

Figure 19 and Figure 20 show the experimental results of the PCC voltage depending on the phase of the reactive current when the ESS operates under the discharging and charging conditions, respectively. In Figure 19 and Figure 20, the magnitudes of the three-phase grid voltages are decreased to 60% as compared with those of phase voltages under normal conditions. Therefore, I_de is determined to 80% (approximately 8.56 A) of I_rating in the grid-connected ESS using the proposed LVRT control strategy. Additionally, I_qe is approximately 6.42 A according to (1).

Figure 19 shows that I_qe is maintained at 6.42 A because the ESS operates under the discharging condition. I_de is changed to 8.56 from −8.56 A, which means that the reactive current injected into the three-phase grid is changed to the capacitive reactive current from the inductive reactive current. In Figure 20, I_qe is maintained at −6.42 A because the ESS operates under the charging condition. I_de is changed similar to that in Figure 19. Depending on the phase of the reactive current injected into the three-phase grid, V_PCC is changed. Regardless of the operating conditions of the ESS, the V_PCC magnitude is larger when the capacitive reactive current is injected as compared with the V_PCC magnitude when the inductive reactive current is injected. In other words, the capacitive reactive current helps in increasing V_PCC regardless of the operation conditions. Therefore, when the grid voltage drops, the capacitive reactive current should be injected into the three-phase grid using the proposed LVRT control strategy; this contributes to an increase of the PCC voltage.

6. Conclusions

This paper presents the LVRT control strategy for grid-connected ESSs. The LVRT requirement for grid-connected ESSs is similar to that for other systems such as WPG and SEG systems. In other words, the reactive current needs to be injected into the three-phase grid based on the LVRT requirement. However, the grid-connected ESSs have bidirectional power flow, unlike other systems that have unidirectional power flow. Therefore, the charging condition of the grid-connected ESSs needs to be considered for the LVRT control strategy. In this paper, the proposed LVRT control strategy for the grid-connected ESSs determines the injection quantity of the active and reactive currents depending on the voltage drop ratio of the three-phase grid. In addition, we analyzed the variations of the PCC voltage depending on the phase of the reactive current in the discharging and charging conditions. As a result, the capacitive reactive current is helpful for increasing V_PCC regardless of the operation condition. Therefore, when the grid voltage drops, the capacitive reactive current needs to be injected into the three-phase grid using the proposed LVRT control strategy. The validity of the proposed LVRT control strategy is verified and the variations of the PCC voltage of the grid-connected ESS are analyzed by simulation and experimental results.