New Reentrant Insulating Phases in Strongly Interacting 2D Systems with Low Disorder
Abstract
:Featured Application
Abstract
1. Introduction
2. New Reentrant Insulating Phases at Low Magnetic Fields
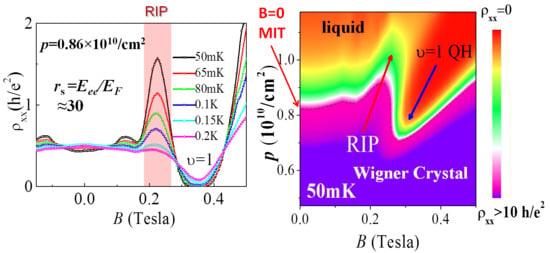
2.1. Resistivity
2.2. Capacitance Measurement
2.3. Inductance
3. Possible Transport Evidence for Intermediate Phases and Wigner Crystal Melting
4. Discussion and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kravchenko, S.V.; Kravchenko, G.V.; Furneaux, J.E.; Pudalov, V.M.; D’Iorio, M. Possible metal-insulator transition at B=0 in two dimensions. Phys. Rev. B 1994, 50, 8039–8042. [Google Scholar] [CrossRef]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef] [Green Version]
- Butler, S.Z.; Hollen, S.M.; Cao, L.; Cui, Y.; Gupta, J.A.; Gutiérrez, H.R.; Heinz, T.F.; Hong, S.S.; Huang, J.; Ismach, A.F.; et al. Progress, Challenges, and Opportunities in Two-Dimensional Materials Beyond Graphene. ACS Nano 2013, 7, 2898–2926. [Google Scholar] [CrossRef] [PubMed]
- Wigner, E. On the Interaction of Electrons in Metals. Phys. Rev. 1934, 46, 1002–1011. [Google Scholar] [CrossRef]
- Klitzing, K.V.; Dorda, G.; Pepper, M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 1980, 45, 494–497. [Google Scholar] [CrossRef]
- Tsui, D.C.; Stormer, H.L.; Gossard, A.C. Two-Dimensional Magnetotransport in the Extreme Quantum Limit. Phys. Rev. Lett. 1982, 48, 1559–1562. [Google Scholar] [CrossRef]
- Abrahams, E.; Anderson, P.W.; Licciardello, D.C.; Ramakrishnan, T.V. Scaling Theory of Localization: Absence of Quantum Diffusion in Two Dimensions. Phys. Rev. Lett. 1979, 42, 673–676. [Google Scholar] [CrossRef]
- Abrahams, E.; Kravchenko, S.V.; Sarachik, M.P. Metallic behavior and related phenomena in two dimensions. Rev. Mod. Phys. 2001, 73, 251–266. [Google Scholar] [CrossRef] [Green Version]
- Spivak, B.; Kravchenko, S.V.; Kivelson, S.A.; Gao, X.P.A. Colloquium: Transport in strongly correlated two dimensional electron fluids. Rev. Mod. Phys. 2010, 82, 1743–1766. [Google Scholar] [CrossRef]
- Qiu, R.L.J.; Gao, X.P.A.; Pfeiffer, L.N.; West, K.W. Connecting the Reentrant Insulating Phase and the Zero-Field Metal-Insulator Transition in a 2D Hole System. Phys. Rev. Lett. 2012, 108, 106404. [Google Scholar] [CrossRef] [PubMed]
- Qiu, R.L.J.; Gao, X.P.A. Qiu and Gao Reply. Phys. Rev. Lett. 2013, 110, 249702. [Google Scholar] [CrossRef] [PubMed]
- Knighton, T.; Wu, Z.; Tarquini, V.; Huang, J.; Pfeiffer, L.N.; West, K.W. Reentrant insulating phases in the integer quantum Hall regime. Phys. Rev. B 2014, 90, 165117. [Google Scholar] [CrossRef]
- Knighton, T.; Tarquini, V.; Wu, Z.; Huang, J.; Pfeiffer, L.; West, K. Large intrinsic inductance in strongly correlated GaAs two-dimensional holes in the integer quantum hall regime. Appl. Phys. Lett. 2014, 104, 193109. [Google Scholar] [CrossRef]
- Shayegan, M. Case for the Magnetic-Field-Induced Two-Dimensional Wigner Crystal. In Perspectives in Quantum Hall Effects; Das Sarma, S., Pinczuk, A., Eds.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- D’Iorio, M.; Pudalov, V.M.; Semenchinsky, S.G. Magnetic field induced transitions between quantized hall and insulator states in a dilute 2D electron gas. Phys. Lett. A 1990, 150, 422. [Google Scholar] [CrossRef]
- Jang, J.; Hunt, B.M.; Pfeiffer, L.N.; West, K.W.; Ashoori, R.C. Sharp tunneling resonance from the vibrations of an electronic Wigner crystal. Nat. Phys. 2017, 13, 340–344. [Google Scholar] [CrossRef]
- Tanatar, B.; Ceperley, D.M. Ground state of the two-dimensional electron gas. Phys. Rev. B 1989, 39, 5005. [Google Scholar] [CrossRef]
- Zhu, X.; Louie, S.G. Variational quantum Monte Carlo study of two-dimensional Wigner crystals: Exchange, correlation, and magnetic-field effects. Phys. Rev. B 1995, 52, 5863. [Google Scholar] [CrossRef]
- Dultz, S.C.; Jiang, H.W. Thermodynamic Signature of a Two-Dimensional Metal-Insulator Transition. Phys. Rev. Lett. 2000, 84, 4689. [Google Scholar] [CrossRef] [PubMed]
- Mermin, N.D.; Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 1966, 17, 1133. [Google Scholar] [CrossRef]
- Brazovskii, S.A. Phase transition of an isotropic system to a nonuniform state. Sov. Phys. JETP 1975, 41, 85. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 1973, 6, 1181. [Google Scholar] [CrossRef]
- Strandburg, K.J. Two-dimensional melting. Rev. Mod. Phys. 1988, 60, 161. [Google Scholar] [CrossRef]
- Halperin, B.I.; Nelson, D.R. Theory of two-dimensional melting. Phys. Rev. Lett. 1978, 41, 121. [Google Scholar] [CrossRef]
- Young, A.P. Melting and the vector Coulomb gas in two dimensions. Phys. Rev. B 1979, 19, 1855. [Google Scholar] [CrossRef]
- Spivak, B.; Kivelson, S.A. Phases intermediate between a two-dimensional electron liquid and Wigner crystal. Phys. Rev. B 2004, 70, 155114. [Google Scholar] [CrossRef]
- Spivak, B.; Kivelson, S.A. Transport in two dimensional electronic micro-emulsions. Ann. Phys. 2006, 321, 2071. [Google Scholar] [CrossRef]
- Falakshahi, H.; Waintal, X. Hybrid phase at the quantum melting of the Wigner crystal. Phys. Rev. Lett. 2005, 94, 046801. [Google Scholar] [CrossRef] [PubMed]
- Drummond, N.D.; Needs, R.J. Phase diagram of the low-density two-dimensional homogeneous electron gas. Phys. Rev. Lett. 2009, 102, 126402. [Google Scholar] [CrossRef] [PubMed]
- Clark, B.K.; Casula, M.; Ceperley, D.M. Hexatic and mesoscopic phases in a 2D quantum Coulomb system. Phys. Rev. Lett. 2009, 103, 055701. [Google Scholar] [CrossRef] [PubMed]
- Jamei, R.; Kivelson, S.A.; Spivak, B. Universal aspects of Coulomb-frustrated phase separation. Phys. Rev. Lett. 2005, 94, 056805. [Google Scholar] [CrossRef] [PubMed]
- Dobrosavljevic, V.; Tanaskovic, D. Chapter 1: Wigner-Mott quantum criticality: From 2D-MIT to 3He and Mott organics. In Strongly Correlated Electrons in Two Dimensions, 1st ed.; Kravchenko, S., Ed.; Pan Stanford Publishing Pte. Ltd.: Singapore, 2017; ISBN 9789814745376. [Google Scholar]
- Camjayi, A.; Haule, K.; Dobrosavljevic, V.; Kotliar, G. Coulomb correlations and the Wigner-Mott transition. Nat. Phys. 2008, 4, 932–935. [Google Scholar] [CrossRef]
- Qiu, R.L.J.; Goble, N.J.; Serafin, A.; Yin, L.; Xia, J.S.; Sullivan, N.S.; Pfeiffer, L.N.; West, K.W.; Gao, X.P.A. Evidence for a New Intermediate Phase in a Strongly Correlated 2D System near Wigner Crystallization. Available online: arXiv:1509.07463 [cond-mat] (accessed on 12 October 2018).
- Brussarski, P.; Li, S.; Kravchenko, S.V.; Shashkin, A.A.; Sarachik, M.P. Transport evidence for a sliding two-dimensional quantum electron solid. Nat. Commun. 2018, 9, 3803. [Google Scholar] [CrossRef] [PubMed]
- Knighton, T.; Wu, Z.; Huang, J.; Serafin, A.; Xia, J.S.; Pfeiffer, L.N.; West, K.W. Evidence of two-stage melting of Wigner solids. Phys. Rev. B 2018, 97, 085135. [Google Scholar] [CrossRef] [Green Version]
- Das Sarma, S.; Hwang, E.H.; Li, Q. Two-dimensional metal-insulator transition as a potential fluctuation driven semiclassical transport phenomenon. Phys. Rev. B 2013, 88, 155310. [Google Scholar] [CrossRef] [Green Version]
- Das Sarma, S.; Hwang, E.H. Two-dimensional metal-insulator transition as a strong localization induced crossover phenomenon. Phys. Rev. B 2014, 89, 235423. [Google Scholar] [CrossRef] [Green Version]
- Das Sarma, S.; Hwang, E.H.; Kechedzhi, K.; Tracy, L.A. Signatures of localization in the effective metallic regime of high-mobility Si MOSFETs. Phys. Rev. B 2014, 90, 125410. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.W.; Johnson, C.E.; Wang, K.L.; Hannahs, S.T. Observation of magnetic-field-induced delocalization: Transition from Anderson insulator to quantum Hall conductor. Phys. Rev. Lett. 1993, 71, 1439. [Google Scholar] [CrossRef] [PubMed]
- Andreev, A.V.; Kivelson, S.A.; Spivak, B. Hydrodynamic Description of Transport in Strongly Correlated Electron Systems. Phys. Rev. Lett. 2011, 106, 256804. [Google Scholar] [CrossRef] [PubMed]
- Levchenko, A.; Xie, H.Y.; Andreev, A.V. Viscous magnetoresistance of correlated electron liquids. Phys. Rev. B 2017, 95, 121301. [Google Scholar] [CrossRef]
- Gao, X.P.A.; Boebinger, G.S.; Mills, A.P.; Ramirez, A.P.; Pfeiffer, L.N.; West, K.W. Spin-polarization-induced tenfold magnetoresistivity of highly metallic two-dimensional holes in a narrow GaAs quantum well. Phys. Rev. B 2006, 73, 241315. [Google Scholar] [CrossRef]
- Dolgopolov, V.T.; Shashkin, A.A.; Kravchenko, S.V. Spin polarization and exchange-correlation effects in transport properties of two-dimensional electron systems in silicon. Phys. Rev. B 2017, 96, 075307. [Google Scholar] [CrossRef]
- Li, S.; Sarachik, M.P. Resistivity of the insulating phase approaching the two-dimensional metal-insulator transition: The effect of spin polarization. Phys. Rev. B 2017, 95, 041301. [Google Scholar] [CrossRef]
- Qiu, R.L.J.; Gao, X.P.A.; Pfeiffer, L.N.; West, K.W. Degenerate versus semidegenerate transport in a correlated two-dimensional hole system. Phys. Rev. B 2011, 83, 193301. [Google Scholar] [CrossRef]
- Mokashi, A.; Li, S.; Wen, B.; Kravchenko, S.V.; Shashkin, A.A.; Dolgopolov, V.T.; Sarachik, M.P. Critical Behavior of a Strongly Interacting 2D Electron System. Phys. Rev. Lett. 2012, 109, 096405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shashkin, A.A.; Kravchenko, S.V.; Dolgopolov, V.T.; Klapwijk, T.M. Sharp increase of the effective mass near the critical density in a metallic two-dimensional electron system. Phys. Rev. B 2002, 66, 073303. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.T. Analysis of the diverging effective mass in YaBa2Cu3O6+x for high-Tc mechanism and pairing symmetry. Int. J. Mod. Phys. B 2018, 32, 1840031. [Google Scholar] [CrossRef]
- Popovic, D. Chapter 5. Metal-insulator transition in correlated two-dimensional systems with disorder. In Strongly Correlated Electrons in Two Dimensions, 1st ed.; Kravchenko, S., Ed.; Pan Stanford Publishing Pte. Ltd.: Singapore, 2017; ISBN 9789814745376. [Google Scholar]








© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, R.L.J.; Liu, C.-W.; Liu, S.; Gao, X.P.A. New Reentrant Insulating Phases in Strongly Interacting 2D Systems with Low Disorder. Appl. Sci. 2018, 8, 1909. https://doi.org/10.3390/app8101909
Qiu RLJ, Liu C-W, Liu S, Gao XPA. New Reentrant Insulating Phases in Strongly Interacting 2D Systems with Low Disorder. Applied Sciences. 2018; 8(10):1909. https://doi.org/10.3390/app8101909
Chicago/Turabian StyleQiu, Richard L. J., Chieh-Wen Liu, Shuhao Liu, and Xuan P. A. Gao. 2018. "New Reentrant Insulating Phases in Strongly Interacting 2D Systems with Low Disorder" Applied Sciences 8, no. 10: 1909. https://doi.org/10.3390/app8101909
APA StyleQiu, R. L. J., Liu, C. -W., Liu, S., & Gao, X. P. A. (2018). New Reentrant Insulating Phases in Strongly Interacting 2D Systems with Low Disorder. Applied Sciences, 8(10), 1909. https://doi.org/10.3390/app8101909