Investigation on Interference Test for Wells Connected by a Large Fracture
Abstract
:Featured Application
Abstract
1. Introduction
2. Methodology
3. Model and Solution for the Interference Test
3.1. Mathematical Model and Pressure Transient Solution
3.2. Extremum Analysis of the Interference Test
3.3. Type-Curve of the Interference Test
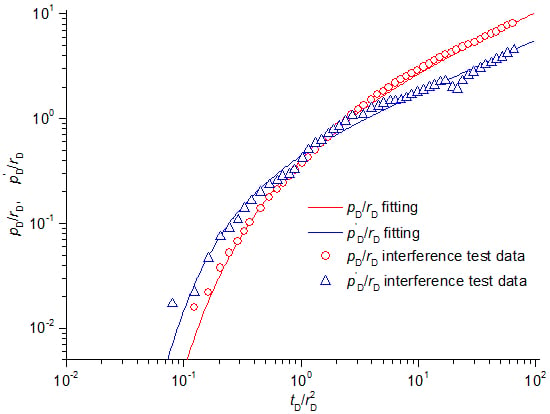
4. Verification of the Interference Test Analysis Model for Wells Connected by a Large Fracture
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Pressure Transient of WsCLF with Crossflow of the Reservoir

References
- Kamal, M.M. Interference and pulse test—A review. J. Petrol. Technol. 1983, 35, 2257–2270. [Google Scholar] [CrossRef]
- Estrada, C.A.; Leung, L.; Majcher, M.B.; Johnson, B. Interference test to Characterize the injection behavior of a 20-Acre pattern in the Court Field. J. Can. Pet. Technol. 2008, 47, 31–38. [Google Scholar] [CrossRef]
- Ohaerl, C.U.; Sankaran, S.; Fernandez, J.J. Evaluation of reservoir connectivity and hydrocarbon resource size in a deep water gas field using multi-well interference tests. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014. SPE 170829. [Google Scholar] [CrossRef]
- Kutasov, I.M.; Eppelbaum, L.V.; Kagan, M. Interference well test-variable fluid flow rate. J. Geophys. Eng. 2008, 5, 86–91. [Google Scholar] [CrossRef]
- AI-Harthi, M.A.; Pardo, C.; Kilany, K.; Otaibi, M.A.; Zeybek, M.; Amin, A. Comprehensive reservoir vertical interference test to optimize horizontal well placement strategy in a giant carbonate field. In Proceedings of the SPE Saudi Arabia Section Annual Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia, 21–23 April 2015. SPE 178013. [Google Scholar] [CrossRef]
- Hocking, G. Hydraulic Pulse interference tests for site hydrogeologic characterization. In Proceedings of the 3rd International Conference on Remediation of Chlorinated and Recalcitrant Compounds, Monterey, CA, USA, 20–23 May 2002. [Google Scholar]
- Akin, S. Design and analysis of multi-well interference tests. In Proceedings of the World Geothermal Congress, Melbourne, Australia, 19–25 April 2015. [Google Scholar]
- Theis, C.V. The relation between lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage. Transactions AGU 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Ogbe, D.O.; Brigham, W.E. A correlation for interference test with well bore storage and skin effects at both wells. SPE Format. Eval. 1989, 3, 391–396. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Witherspoon, P.A. A method of analyzing pump test data from fractured aquifers. In Proceedings of the Symposium on Percolation through Fissured Rocks, International Society for Rocks Mechanics, Stuttgart, Germany, 18–19 September 1972; Volume 3-B, pp. 1–9. [Google Scholar]
- Chu, L.; Grader, A.S. Transient pressure analysis of three wells in a three-composite reservoir. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 6–9 October 1991. SPE 22716. [Google Scholar] [CrossRef]
- Onur, M.; Reynolds, A.C. Interference test of a two-layers commingled reservoir. SPE Format. Eval. 1989, 4, 595–603. [Google Scholar] [CrossRef]
- Slack, T.Z. Hydromechanical Interference Slug Tests in a Fractured Biotite Geniss. Master’s Thesis, Clemson University, Clemson, SC, USA, July 2010. [Google Scholar]
- Martinez, N.R.; Samaniego, F.V. Advance in the analysis of pressure interference tests. J. Can. Pet. Technol. 2010, 49, 65–70. [Google Scholar] [CrossRef]
- Malekzadeh, D.; Tiab, D. Interference test of horizontal wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 6–9 October 1991. SPE 22733. [Google Scholar] [CrossRef]
- AI-Khamis, M.; Ozkan, E.; Raghavan, R. Interference test with horizontal observation wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–3 October 2001. SPE 71581. [Google Scholar] [CrossRef]
- Awotunde, A.A. Characterization of reservoir parameters using horizontal well interference test. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. SPE 106517. [Google Scholar] [CrossRef]
- Sheng, J.J. A new technique to determine horizontal and vertical permeabilities from the time-Delayed response of a vertical interference test. Transport Porous Med. 2009, 77, 507–527. [Google Scholar] [CrossRef]
- Hounli, A.; Tiab, D. Analysis of interference test of horizontal wells in an anisotropic medium. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Perth, Australia, 18–20 October 2004. SPE 88537. [Google Scholar] [CrossRef]
- Awotunde, A.A.; Ai-Hashim, H.S.; AI-Khamis, M.N.; AI-Yousef, H.Y. Interference test using finite-conductivity horizontal wells of unequal lengths. In Proceedings of the SPE Eastern Regional/AAPG Eastern Section Joint Meeting, Pittsburgh, PA, USA, 11–15 October 2008. SPE 117744. [Google Scholar] [CrossRef]
- Syed, A.F.; AI-Hashim, H.S. Interference test with horizontal wells in layered reservoir. In Proceedings of the Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 30 October–1 November 2007. SPE 109023. [Google Scholar] [CrossRef]
- Adewole, E.S. Mathematical formulation of interference tests analyses procedure for horizontal and vertical wells both in a laterally infinite layered reservoir. Petrol. Sci. Technol. 2013, 3, 680–690. [Google Scholar] [CrossRef]
- AI-Farhan, F.A.; Gazi, N.H.; AI-Naqi, M.; Ali, F.; Dasti, L.; AI-Qattan, A. Reservoir connectivity analysis using long term interference test in a waterflood pilot in the carbonate Marrat formation of the greater Burgan Field, Kuwait. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012. SPE 159126. [Google Scholar] [CrossRef]
- AI-Farhan, F.A.; Gazi, N.H.; AI-Humoud, J.; Tirkey, N.; Haryono, R. An interference test coupled with a drawdown analysis of horizontal well using a multi-phase flow meter to evaluate reservoir parameters and connectivity. In Proceedings of the Abu Dhabi International Petroleum Conference and Exhibition, Abu Dhabi, UAE, 11–14 November 2012. SPE 161711. [Google Scholar] [CrossRef]
- Nurafza, P.R.; AI-Shamma, B.; Feng, W.C. Interference test of horizontal producers and injectors in the Huntington. In Proceedings of the International Petroleum Technology Conference, Doha, Qatar, 19–22 January 2014. IPTC 17586. [Google Scholar] [CrossRef]
- Koening, R.A.; Stubbs, P.B. Interference test of a coalbed methane reservoir. In Proceedings of the SPE Unconventional Gas Technology Symposium, Louisville, KY, USA, 18–21 May 1986. SPE 15225. [Google Scholar] [CrossRef]
- Ajani, A.A.; Kelkar, M.G. Interference study in shale Plays. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 6–8 February 2012. SPE 151045. [Google Scholar] [CrossRef]
- Kazemi, H.; Seth, M.S.; Thomas, G.W. The interpretation of interference tests in naturally fractured reservoirs with uniform fracture distribution. SPE J. 1969, 9, 463–472. [Google Scholar] [CrossRef]
- Vasilev, I.; Aleksakhin, Y. Interference test in naturally fractured formation gas field case study. In Proceedings of the SPE Russian Petroleum Technology Conference and Exhibition, Moscow, Russia, 24–26 October 2016. SPE 181969. [Google Scholar] [CrossRef]
- Araujo, H.N.; Andina, S.A.; Gilman, J.R.; Kazemi, H. Analysis of interference and pulse tests in heterogenous naturally fractured reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 27–30 September 1998. SPE 49234. [Google Scholar] [CrossRef]
- Biryukov, D.; Kuchuk, F.J. Transient pressure behavior of reservoirs with discrete conductive faults and fractures. Transport Porous Med. 2012, 95, 239–268. [Google Scholar] [CrossRef]
- Seth, P.; Manchanda, R.; Kumar, A.; Sharma, M. Estimating hydraulic fracture geometry by analyzing the pressure interference between fractured horizontal wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018. SPE 191492. [Google Scholar] [CrossRef]
- Weijermars, R.; van Harmelen, A.; Zuo, L.; Alves, I.N.; Yu, W. Flow interference between hydraulic fractures. SPE Reserv. Eval. Eng. 2018, 21, 942–960. [Google Scholar] [CrossRef]
- Morales, A.; Zhang, K.; Gakhar, K.; Porcu, M.M.; Lee, D.; Shan, D.; Malpani, R.; Pope, T.; Sobernheim, D.; Acock, A. Advanced modeling of interwell fracturing interference: An Eagle Ford shale oil study-refracturing. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 9–11 February 2016. SPE 179177. [Google Scholar] [CrossRef]
- Chu, W.; Scott, K.; Flumerfelt, R.; Chen, C. A new technique for quantifying pressure interference in fractured horizontal shale wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018. SPE 191407. [Google Scholar] [CrossRef]
- Wu, K.; Wu, B.; Yu, W. Mechansim analysis of well interference in unconventional reservoirs: Insights from fracture-geometry simulation between two horizontal wells. SPE Prod. Oper. 2018, 33, 1–9. [Google Scholar] [CrossRef]
- Xiao, C.; Dai, Y.; Tian, L.; Lin, H.; Zhang, Y.; Yang, Y.; Hou, T.; Deng, Y. A semianalytical methodology for pressure-transient analysis of multiwall-pad-production scheme in shale gas reservoirs, part 1: New insights into flow regimes and multiwall interference. SPE J. 2018, 23, 1–21. [Google Scholar] [CrossRef]
- Bourdet, D. Well Test Analysis: The Use of Advanced Interpretation Models; Elsevier Science B.V.: Amsterdam, The Netherlands, 2002; pp. 273–299. [Google Scholar]
- Liu, W.; Yao, J.; Wang, Y. Exact analytical solutions of moving boundary problems of one-dimensional flow in semi-infinite long porous media with threshold pressure gradient. Int. J. Heat. Mass Tran. 2012, 55, 6017–6022. [Google Scholar] [CrossRef]
- Liu, N. Practical Modern Well Test Interpretation Method, 5th ed.; Petroleum Industry Press: Beijing, China, 2008; p. 290. [Google Scholar]
- Deruyck, B.G.; Bourdet, D.P.; Da Prat, G.; Ramey, H.J., Jr. Interpretation of interference tests in reservoirs with double porosity behavior-theory and field examples. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 26–29 September 1982. SPE 11025. [Google Scholar] [CrossRef]
- Lee, S.T.; Brockenbrough, J.R. A new approximate analytic solution for finite-conductivity vertical fractures. SPE Forma. Eval. 1986, 1, 75–88. [Google Scholar] [CrossRef]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, G.; Liu, Y.; Liu, W.; Gao, D. Investigation on Interference Test for Wells Connected by a Large Fracture. Appl. Sci. 2019, 9, 206. https://doi.org/10.3390/app9010206
Han G, Liu Y, Liu W, Gao D. Investigation on Interference Test for Wells Connected by a Large Fracture. Applied Sciences. 2019; 9(1):206. https://doi.org/10.3390/app9010206
Chicago/Turabian StyleHan, Guofeng, Yuewu Liu, Wenchao Liu, and Dapeng Gao. 2019. "Investigation on Interference Test for Wells Connected by a Large Fracture" Applied Sciences 9, no. 1: 206. https://doi.org/10.3390/app9010206
APA StyleHan, G., Liu, Y., Liu, W., & Gao, D. (2019). Investigation on Interference Test for Wells Connected by a Large Fracture. Applied Sciences, 9(1), 206. https://doi.org/10.3390/app9010206