Thermodynamic Simulations for Determining the Recycling Path of a Spent Lead-Acid Battery Electrolyte Sample with Ca(OH)2

Gu, Shuai; Fu, Bitian; Fujita, Toyohisa; Ahn, Ji Whan

doi:10.3390/app9112262

Open AccessCommunication

Thermodynamic Simulations for Determining the Recycling Path of a Spent Lead-Acid Battery Electrolyte Sample with Ca(OH)₂

by

Shuai Gu

¹

,

Bitian Fu

²,

Toyohisa Fujita

³ and

Ji Whan Ahn

^1,*

¹

Center for Carbon Mineralization, Mineral Resources Division, Korea Institute of Geoscience and Mineral Resources, 124 Gwahak-ro, Gajeong-dong, Yuseong-gu, Daejeon 34132, Korea

²

Shanghai Environment Sanitation Engineering Design and Research Institute Co. Ltd., Shanghai 200232, China

³

School of Resources, Environment, and Materials, Guangxi University, 100 Daxue Rd, Nanning 530004, China

^*

Author to whom correspondence should be addressed.

Appl. Sci. 2019, 9(11), 2262; https://doi.org/10.3390/app9112262

Submission received: 9 May 2019 / Revised: 22 May 2019 / Accepted: 27 May 2019 / Published: 31 May 2019

(This article belongs to the Special Issue Electronic Waste: Management and Recovery Technologies)

Download

Browse Figures

Versions Notes

Abstract

:

Featured Application

This thermodynamic simulation can help design the recycling process of spent lead-acid battery electrolyte. The effect of ambient CO₂ and pH can be simulated by thermodynamic calculations.

Abstract

By utilizing thermodynamic calculations, the possible removal path of spent lead-acid battery electrolytes was modeled. The process was divided into precipitation and carbonation processes. In the carbonation process, two scenarios were discussed, namely carbonation with and without pre-filtration of the precipitates resulted from the precipitation process. The results showed that in the precipitation process, the theoretical limit for the chemical removal of SO₄²⁻ was 99.15%, while in the following carbonation process without filtration, only 69.61% of SO₄²⁻ was removed due to the fact that CO₂ reacts with Ca²⁺ ion in the solution, and thus leads to the production of CaCO₃ and SO₄²⁻ ions in the solution. In the carbonation process without filtration, with the increase of CO₂ in the solution the removal ratio of SO₄²⁻ further decreases. Thermodynamic simulation was effective in predicting the theoretical removal limits and helps in understanding and optimizing the removal process.

Keywords:

thermodynamic simulations; spent lead-acid battery; electrolyte; carbonation

Graphical Abstract

1. Introduction

Lead-acid batteries (LAB) are widely used in motor vehicles [1,2], backup power supplies [3], and stand-alone power systems [4,5] due to their properties of excellent reliability, low cost, good operation life, high surge currents, and relatively large power-to-weight ratio [6]. LABs, as the single most-used battery system worldwide, consume approximately 85% of the total global lead production [7]. To satisfy the huge and ever-increasing demand for lead worldwide, in 2014 alone 2.46 million tons of secondary lead was recovered from spent LABs. [8] The first step in the recycling process is disassembly, in which spent LABs are separated into four parts, i.e., the grid, with the main composition being lead (92~95%), lead paste, which is mainly composed of lead oxide (PbO), lead dioxide (PbO₂), lead sulfate (PbSO₄), and lead (Pb) plastics, which are the main composition of shells, and electrolytes, with the main composition being sulfate acid (38 wt.% H₂SO₄). The grid separated from spent LABs is commonly refined for utilization in the manufacture of new LABs [9]. The lead paste has been intensively studied with various hydrometallurgy and pyrometallurgy techniques [10,11,12,13,14]; shells are also recovered as polypropylene for manufacturing new LABs [15,16], and the electrolytes are normally collected for further purification [8]. However, in spent LAB recycling plants, installation of new devices is required to collect and handle the highly corrosive electrolytes. In a typical disassembly and refinery plant, spent electrolytes are often discharged onto the ground and collect in a pit, which makes the purification process unreasonable for recycling. The typical recycling methods of SO₄²⁻ ions from wastewater include: adsorption [17], chemical precipitation [18,19], biological treatment [20], and ion exchange [21]. Due to the high concentrations of SO₄²⁻ in the spent electrolytes, chemical precipitation was adopted. BaCl₂ [22], limestone [19], and ettringite [23] have been used to remove SO₄²⁻ in wastewater, while no detailed theoretical calculation has been reported. In this paper, the systematic theoretical calculations of spent LAB electrolytes’ reactions with Ca(OH)₂ were conducted, and sulfate ions were then recovered as CaSO₄·2H₂O. Thermodynamic calculations were utilized to simulate the whole process, based on which the optimum conditions and recycling path were obtained. The thermodynamic simulation predicted the theoretical chemical precipitation removal efficiency and suggested that ambient CO₂ should be avoided in the precipitation process and filtration should be adopted before the carbonation process to achieve higher efficiency.

2. Materials and Methods

2.1. Materials

The spent LAB electrolyte sample was received from Dansuk Industrial Co., Ltd., Gyeonggi-do, Korea. The spent electrolyte sample was first filtered and analyzed with Inductively coupled plasma-optical emission spectrometry (ICP-OES) to measure the concentration of SO₄²⁻ ions. The concentration of SO₄²⁻ in the spent electrolyte was 147,000 mg/L. The main impurities of the spent electrolyte were Ca²⁺, Mg²⁺, and Pb²⁺ (3.01 mg/L). Due to the low concentrations of both Ca²⁺ and Mg²⁺ and the fact that both ions are not toxic, only Pb²⁺ was discussed in detail in this research. The pH of the spent electrolyte solution was measured with a Thermo Scientific^TM Orion^TM Versa Star Pro^TM pH meter equipped with a highly sensitive ROSS Ultra 8302BNUMD electrode, with the mean pH being −0.53.

2.2. Methods

The thermodynamic calculations were carried out with Matlab^® R2010a software using thermodynamic parameters of all possible reactions. At the first stage, spent H₂SO₄ from the electrolyte sample was precipitated with Ca(OH)₂ powder until the solution was almost saturated calcium hydroxide, then the carbonation processes were simulated, both with and without pre-filtration of the precipitates resulted from the precipitation process. All simulations were performed under the condition that the temperature was kept at 25 °C at all times. Equations (1)–(3), (4)–(13), and (14)–(21) from Table 1 were used in the calculation of the thermodynamic equilibrium distributions of the saturated solutions of Ca(OH)₂, CaCO₃, and CaSO₄·2H₂O, respectively, while Equations (21)–(29) and (30)–(43) from Table 1 were utilized to calculate the thermodynamic distributions of different species during the precipitation process and carbonation process after filtration of the precipitates. Equations (44)–(47), together with Equations (23), (24), (26)–(29), (34), (35), (37), and (39) from Table 1, were utilized to calculate the carbonation process without the filtration of precipitates resulted from the precipitation process. Equations (48)–(55) and (56)–(61) from Table 1 were used to calculate the thermodynamic distributions of Pb²⁺ in precipitation and carbonation processes, respectively. All species (aqueous species and precipitates) at different pH can be obtained by solving the matrix of equilibrium constants and mass balances.

It is worth pointing out that in the modeling process of carbonation, the system was considered as a closed system with a certain amount of CO₂ injected into the system. This was adopted due to the fact that CO₂ was the gas and the amount of CO₂ consumed cannot be easily obtained.

Due to the fact that calcium, sulfate, and carbonate are all divalent ions with quite low ionic activity coefficients (γ), which are γ_Ca²⁺ = 0.28 (I = 0.7, 25 °C and 1 atm), γ_SO_4²⁻ = 0.12, and γ_CO_3²⁻ = 0.20 (I = 0.7, 25 °C and 1 atm), respectively, the activity corrections are needed in the thermodynamic modeling process. The definition of ionic strength (I) and activity coefficient are shown in Equations (1) and (2) [24]:

I = 1 / 2 \sum m_{i} Z_{i}^{2}

(1)

γ_{i} = \frac{a_{i}}{m_{i}}

(2)

where m_i is the molality of an aqueous species, i is the corresponding aqueous species, Z_i is the charge of i, a_i is activity of species i, and γ_i is the activity coefficient of species i. In this study, a simplified Helgeson-Kirkham-Flowers model was used to calculate the activity coefficient, as shown in Equation (3) [25,26,27]:

L o g γ_{i} = - A Z_{i}^{2} (\sqrt{\frac{I}{1 + B \sqrt{I}}}) - L o g (1 + 0.018 \sum m_{k}) + b I

(3)

where A is the Debye-Hückel slope, B is the distance of the closest approach, b is a solute specific parameter, and k is all solute species in the aqueous solution.

3. Results

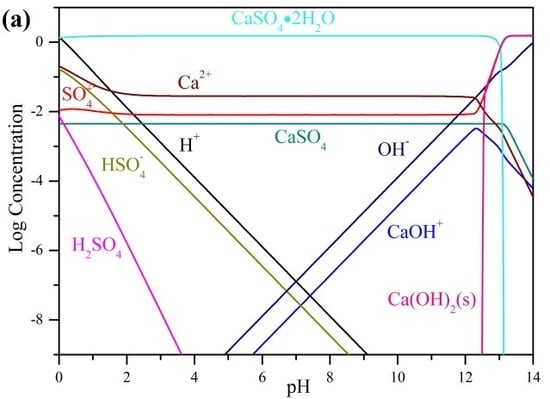
3.1. Precipitation

Figure 1 shows the thermodynamic calculations of 30 mM Ca(OH)₂ in aqueous solution at 25 °C with different pH. The theoretical values were obtained by solving the matrix consisting of both equilibrium constants (Equations (2) and (3) from Table 1) and mass balances (Equations (4) and (5)). With Matlab, this set of equations were simultaneously solved with 100 steps in the whole pH range (0~14), thus giving the distribution of each species at different pH. In the case of Ca(OH)₂ solution, four species, Ca²⁺, CaOH⁺, OH⁻, and Ca(OH)₂(s), were taken into consideration. Figure 1a shows the log concentrations of different species in 30 mM Ca(OH)₂ solution with different pH. Log concentrations were adopted due to the low concentrations of each species. As can be seen, with the increase of pH the concentration of Ca²⁺ first stays unchanged when pH < 12.6, while with the further increase of pH, the concentration of Ca²⁺ decreased slowly, and at the same time Ca(OH)₂(s) emerged in the solution as a precipitate. CaOH⁺ ions started to appear at pH 6, the log concentration of which increased linearly until pH 12.6, after which the log concentration of CaOH⁺ ions started to decrease linearly. In Figure 1b, the fraction of calcium was calculated vs. pH, and a similar change of concentration was also observed for Ca²⁺, CaOH⁺, and Ca(OH)₂. The theoretical parameters of saturated Ca(OH)₂ are shown in Table 1; as can be seen, the theoretical pH of saturated Ca(OH)₂ is 12.45 with C_Ca²⁺ = 19.48 mM. Similarly, the equilibrium distributions of saturated CaCO₃ solution can be calculated by solving the matrix composed of Equations (4)–(13) from Table 1 (thermodynamic parameters) and (6)–(8) (mass balances). The distributions of different species in CaCO₃ solution was also shown in Figure 2 and Table 1. As can be seen, for the saturated solution of CaCO₃, the equilibrium pH is 9.94 and C_Ca²⁺ = 0.1415 mM. For the saturated CaCO₃ solution, if the pH is high enough (pH > 13), Ca²⁺ from CaCO₃(s) will dissolve into solution and form Ca(OH)₂(s), thus causing the increase of concentration of free Ca²⁺ ions. As for saturated CaSO₄ solution (Figure 3), the equilibrium pH is 7.08 and the equilibrium C_Ca²⁺ = 12.03 mM. In the saturated solution of CaSO₄, the main precipitate would be CaSO₄·2H₂O; as can be seen from Figure 3b, with the increase of pH CaSO₄·2H₂O starts to decrease at pH 11 and the dominant precipitate becomes Ca(OH)₂(s) at approximately pH 13. Therefore, for recovering CaSO₄·2H₂O, the pH should be controlled properly. By comparing the data in Figure 1 and Figure 2, it is clear that the equilibrium concentration of Ca²⁺ in CaCO₃ solution was significantly smaller than that in Ca(OH)₂ solution, which was caused by the much smaller solubility products (K_sp) of CaCO₃, and should carbonation happen in the precipitation process the concentration of Ca²⁺ should also decrease, which would, in turn, cause the increase of SO₄²⁻. Based on the results obtained from Figure 1, Figure 2 and Figure 3, we conclude that the saturated CaCO₃ solution has the lowest equilibrium C_Ca²⁺, and contacting with CO₂ might decrease the concentration of Ca²⁺ ions, which will help us better understand the carbonation process discussed in Section 3.2. The detailed species distribution of saturated Ca(OH)₂, CaCO₃ and CaSO₄ can be found in Table 2.

C_{C a^{2 +}} + C_{C a {(O H)}_{2} (s)} + C_{C a O H^{+}} = C a_{t o t a l}

(4)

2 \times C_{C a^{2 +}} + C_{C a O H^{+}} = C_{O H^{-}}

(5)

C_{C a C O_{3} (s)} + C_{C a C O_{3}} + C_{C a H C O_{3}} + C_{C a^{2 +}} = C_{C a_{t o t a l}}

(6)

\begin{array}{l} C_{C a C O_{3} (s)} + C_{C a C O_{3}} + C_{C a H C O_{3}} + C_{C O_{3}^{2 -}} + C_{H C O_{3}^{-}} + C_{H_{2} C O_{3}} + C_{C O_{2}} + C_{C O_{2} (g)} \\ = C_{C O_{3}^{2 -}_{t o t a l}} \end{array}

(7)

C_{C a H C O_{3}} + C_{H C O_{3}^{-}} + 2 \times (C_{H_{2} C O_{3}} + C_{C O_{2}} + C_{C O_{2} (g)}) = C_{O H^{-}}

(8)

According to the ICP-OES measurement results, the concentration of SO₄²⁻ in the spent electrolyte sample was 1.53 M. Figure 4 shows the reaction equilibriums of 1.53 M SO₄²⁻ reacting with 1.55 M Ca(OH)₂ at different pH. Extra Ca(OH)₂ was introduced to ensure the removal of SO₄²⁻ ions. As can be seen from Figure 4, the main precipitates were CaSO₄·2H₂O in a wide pH range (pH: 2~12), according to Equation (9), and when pH < 2 [19], CaSO₄·2H₂O would dissolve into the solution and become Ca²⁺ and SO₄²⁻ ions, according to Equation (10). At the same time, if pH > 12, the ratio of CaSO₄·2H₂O might also decrease because of the formation of Ca(OH)₂(s) (Figure 4c) and SO₄²⁻ (Figure 4b), according to Equation (11). The final pH and composition of the mixture are shown in Table 3; as can be seen, the equilibrium pH of the mixture is 12.42 with C_Ca²⁺ = 25.06 mM, C_SO_4²⁻ = 8.668 mM, and C_CaSO_4·2H_2O = 1517 mM. Based on these data, the removal ratio of SO₄²⁻ can be calculated and shown in Table 3. Also, by comparing the data obtained from the precipitation process with the saturated CaCO₃ and CaSO₄ solution data, the result indicates that if CO₂ was introduced in the precipitation process, the removal efficiency of SO₄²⁻ might decrease. Therefore, ambient CO₂ should be avoided in the precipitation process to obtain a higher removal efficiency. Also, the theoretical results obtained in this model are very close to the experimental results of Fang et al. [23].

Ca (OH)_{2} (s) + H_{2} {SO}_{4} \leftrightarrow {CaSO}_{4} \cdot 2 H_{2} O (s)

(9)

{CaSO}_{4} \cdot 2 H_{2} O (s) + H^{+} \leftrightarrow {HSO}_{4}^{-} + {Ca}^{2 +} + 2 H_{2} O

(10)

{CaSO}_{4} \cdot 2 H_{2} O (s) + 2 {OH}^{-} \leftrightarrow Ca (OH)_{2} (s) + {SO}_{4}^{2 -} + 2 H_{2} O

(11)

Figure 5 shows the distributions of lead-related ions at different pH. As can be seen from Figure 5a, no precipitation was formed in the whole pH range due to the extremely low concentration of lead and the existence of SO₄²⁻ (Table 3). [28] This might be in favor of the precipitation process due to the fact that lead is toxic, and according to this simulation, no lead was precipitated in the precipitation process with Ca(OH)₂. Figure 5b shows the fraction of lead at different pH, based on which the distribution of lead can be divided into three regions: at low pH region (pH < 2), the main form of lead is Pd²⁺; at moderate pH region (2 < pH < 7), lead was mainly in the form of PbSO₄ (Equation (52) from Table 1); at high pH region (pH > 7), lead forms a complex with OH⁻ ions and forms four kinds of complexes with the increase of pH (Equations (48)–(51) from Table 1).

3.2. Carbonation

After the precipitation process, the extra Ca(OH)₂ should be removed and the carbonation process introduced to both remove extra Ca(OH)₂ and neutralize the solution. Due to the fact that the appearance of CO₂ might promote the production of CaCO₃, which in turn might influence the final products of the carbonation process, the carbonation process was divided into 2 scenarios: with filtration and without filtration of the precipitates resulted from the precipitation process, respectively. In the filtration and carbonation scenario, the total calcium concentration (T_Ca) T_Ca = C_Ca²⁺ + C_CaOH+ + C_CaSO₄ = 33.122 mM, while the total sulfate concentration (T_SO₄²⁻) T_SO₄²⁻ = C_SO₄²⁻ + C_CaSO₄ = 13.125 mM. Figure 6 shows the calculated species distributions of the carbonation process after filtration; as can be seen, the main precipitate when pH > 6 was CaCO₃ (Equation (12)), while in the pH range of 3~5 the main precipitate was CaSO₄·2H₂O (Equation (43) from Table 1). As shown in Figure 6b, with the increase of pH the ratio of calcium in Ca²⁺ ion form decreases and the ratio in CaCO₃ form increases, which was caused by the formation of CaCO₃ in the alkaline region (Equation (12)). As can be seen from Figure 6c, when the pH > 7, the dominant species is SO₄²⁻, because the dissociation of CaSO₄ (Equation (13)) and the dissociation of CaSO₄ were caused by the constant removal of Ca²⁺ according to Equation (12). When the final pH is 7, the equilibrium species distributions are shown in Table 3; as can be seen, the equilibrium C_[Ca²⁺_] = 0.4509 mM, C_[SO_4²⁻_] = 13.01 mM, and the main precipitate was CaCO₃(s) (32.44 mM).

{Ca}^{2 +} + {CO}_{2} + 2 {OH}^{-} \leftrightarrow {CaCO}_{3} (s) + H_{2} O

(12)

{CaSO}_{4} \leftrightarrow {Ca}^{2 +} + {SO}_{4}^{2 -}

(13)

In the case of carbonation without filtration, the total calcium concentration is T_ca = 1.55 M, and the total sulfate concentration is T_SO_4²⁻= 1.53 M. As can be seen from Figure 7, the dominant precipitated species were CaSO₄·2H₂O (pH: 2~5, Equation (9)), CaSO₄·2H₂O and CaCO₃ (pH: 5~13, Equations (9) and (12)), and Ca(OH)₂(s) and CaCO₃ (pH: 13~14, Equations (11) and (12)), respectively. When pH is smaller than 2, a certain amount of CaSO₄·2H₂O would dissolve, as can be seen from Figure 7b (Equation (10)). The decrease of C_CaSO_4·2H_2O in pH 5–7 was mainly caused by the formation of CaCO₃ (Equation (12)), which leads to the dissolution of CaSO₄·2H₂O (Equation (14)), and simultaneously results in the increase of C_SO_4²⁻ in the same region. In other words, this decrease of C_CaSO_4·2H_2O in pH 5–7 resulted from the combination of CaSO₄·2H₂O dissolution reactions (Equation (14)) and carbonation reaction (Equation (12)). When pH is larger than 13, the fraction of CaSO₄·2H₂O further decreases to almost zero; this was caused by both the formation of CaCO₃ (Equation (12)), and most importantly, the formation of Ca(OH)₂(s) (Equation (11)) at extremely high pH. The fraction of CaSO₄·2H₂O decreases with the increase of CO₂ concentrations, according to Figure 7b–d. To obtain a higher removal ratio of SO₄²⁻, 0.1 M CO₂ was chosen. The equilibrium species distributions of the solution at pH 7 are listed in Table 3; the equilibrium C_Ca²⁺ = 4.098 mM, C_SO_4²⁻= 460.43 mM, C_CaCO_3(s) = 476.2 mM, and C_CaSO_4·2H_2O = 1065 mM. The calculated removal ratio of sulfate, in this case, is lower (69.61%) than the carbonation after filtration (99.15%).

{CaSO}_{4} \cdot 2 H_{2} O (s) \leftrightarrow {Ca}^{2 +} + {SO}_{4}^{2 -} + 2 H_{2} O

(14)

Since carbonation with filtration was a better option than carbonation without filtration, only carbonation with filtration was calculated for lead (Figure 8). As can be seen from Figure 8a, the PbCO₃(s) precipitate (Equation (61) from Table 1) existed in the moderate pH region (5 < pH < 9); when pH is lower than this value PbCO₃(s) might react with H⁺ to form PbHCO₃⁺, according to Equation (15), while at a higher pH with the increase of pH, PbCO₃(s) might react with both CO₃²⁻ and OH⁻ to form Pb₃(CO₃)₂OH₂(s) (Equation (16)), Pb(CO₃)₂²⁻ (Equation (17)), PbCO₃OH⁻ (Equation (18)), and Pb(OH)₃⁻ (Equation (19)), respectively. The end pH = 7 was adopted for the carbonation process, in which 96.35% of lead was precipitated as PbCO₃(s), and thus stabilized with CaCO₃ in the carbonation process (Table 3).

{PbCO}_{3} (s) + H^{+} \leftrightarrow {PbHCO}_{3}^{+}

(15)

3 {PbCO}_{3} (s) + 2 {OH}^{-} \leftrightarrow {Pb}_{3} ({CO}_{3})_{2} {OH}_{2} (s) + {CO}_{3}^{2 -}

(16)

{PbCO}_{3} (s) + {CO}_{3}^{2 -} \leftrightarrow Pb ({CO}_{3})_{2}^{2 -}

(17)

{PbCO}_{3} (s) + {OH}^{-} \leftrightarrow {PbCO}_{3} {OH}^{-}

(18)

{PbCO}_{3} (s) + 3 {OH}^{-} \leftrightarrow Pb (OH)_{3}^{-} + {CO}_{3}^{2 -}

(19)

4. Conclusions

Normally, the spent LAB electrolytes can be directly filtered and reused on the condition that the electrolytes were collected and handled properly in the dissembling plant. For dissembling plants without appropriate collecting setups, electrolytes are often polluted with foreign ions, since electrolytes are often discharged onto the ground directly. These polluted electrolytes cannot be purified by simple filtration, and thus require more reasonable recycling techniques. Instead, it is more reasonable and profitable to recycle and stabilize SO₄²⁻ in the form of CaSO₄·2H₂O, which can be widely used as a fertilizer and for building materials. In this study, the polluted electrolyte sample was recycled with chemical precipitation and carbonation techniques. To understand the whole recycling process, thermodynamic simulations in the precipitation and carbonation processes were conducted. The thermodynamic calculations of saturated Ca(OH)₂, CaCO₃, and CaSO₄ solutions helped us to understand the whole process, since Ca(OH)₂ and CaSO₄ appear in both precipitation and carbonation processes when the pH is higher than 13. Additionally, CaCO₃ appears in the carbonation process with and without filtration. The theoretical limit for the removal ratio of SO₄²⁻ was predicted to be 99.15% with 1.53 M SO₄²⁻ and 1.55 M Ca(OH)₂. Also, by comparing the carbonation process with and without pre-filtration of the precipitates obtained from the precipitation process, the theoretical removal efficiency of SO₄²⁻ was calculated to be 99.15% and 69.61%, respectively. With the increase of CO₂ concentrations in the solution, the removal efficiency of SO₄²⁻ further decreased. Furthermore, the chemical precipitation and carbonation of lead in the spent electrolyte sample were calculated; no precipitation existed in the precipitation process due to the appearance of SO₄²⁻, while 96.35% of lead was precipitated as PbCO₃(s) in the carbonation process, which stabilized lead with CaCO₃. The thermodynamic calculations helped us to design and understanding the whole removal process quantitatively. Based on the thermodynamic calculation results, the optimized removal process of SO₄²⁻ should be precipitation without contact with ambient CO₂, since PbCO₃ might precipitate around pH 9, which would lead to the existence of lead in CaSO₄·2H₂O. Additionally, filtration should be undertaken before the carbonation process to avoid the re-dissolution of CaSO₄·2H₂O. After filtration, the final product of the recycling process (CaSO₄·2H₂O) is obtained. In the following carbonation process, the flow rate of CO₂ and pH should be controlled properly to stabilize lead and extra calcium in the form of PbCO₃ and CaCO₃, respectively. At last, after chemical precipitation and carbonation, there is still around 13 mM SO₄²⁻ in the solution, which needs to be removed by adsorption or ion-exchange techniques. The overall theoretical chemical precipitation limit for removal of SO₄²⁻ was 99.15%. The limitation of the simulation was: (1) in the simulation process of carbonation, where the system was assumed to be a closed system with all CO₂ dissolved in the solution; and (2) equilibrium at each pH is achieved by both carbonation reaction and addition of HCl or NaOH when needed. These limitations might cause the deviation of simulation values from experimental results, however, the tendency of the whole process should be similar, which makes the simulation of the carbonation process a good tool for reference.

Author Contributions

Conceptualization, T.F. and J.W.A.; data curation, B.F.; formal analysis, B.F.; investigation, S.G.; methodology, S.G.; project administration, J.W.A.; resources, J.W.A.; software, B.F.; supervision, T.F. and J.W.A.; validation, S.G., B.F., and J.W.A.; visualization, B.F.; writing—original draft, S.G.; writing—review and editing, T.F.

Funding

This research was supported by the National Strategic Project-Carbon Mineralization Flagship Center of the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (MSIT), the Ministry of Environment (ME) and the Ministry of Trade, Industry and Energy (MOTIE). (2017M3D8A2084752).

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

Bode, H. Lead-Acid Batteries; U.S. DOE: Washington, DC, USA, 1977; pp. 1–15.
Bhangu, B.S.; Bentley, P.; Stone, D.A.; Bingham, C.M. Nonlinear observers for predicting state-of-charge and state-of-health of lead-acid batteries for hybrid-electric vehicles. IEEE Trans. Veh. Technol. 2005, 54, 783–794. [Google Scholar] [CrossRef]
Parker, C.D. Lead–acid battery energy-storage systems for electricity supply networks. J. Power Sources 2001, 100, 18–28. [Google Scholar] [CrossRef]
Zou, G.; Dou, Y.; Chang, X.; Chen, Y. Design and application of a standalone hybrid wind-solar system for automatic observation systems used in the polar region. Appl. Sci. 2018, 8, 2376. [Google Scholar]
Chang, Y.; Mao, X.; Zhao, Y.; Feng, S.; Chen, H.; Finlow, D. Lead-acid battery use in the development of renewable energy systems in China. J. Power Sources 2009, 191, 176–183. [Google Scholar] [CrossRef]
Pavlov, D. Lead-Acid Batteries: Science and Technology, 1st ed.; Elsevier Science: Oxford, UK, 2011; pp. 21–26. [Google Scholar]
Recycling Used Lead-Acid Batteries: Health Considerations. Available online: https://apps.who.int/iris/bitstream/handle/10665/ (accessed on 31 May 2019).
Sun, Z.; Cao, H.; Zhang, X.; Lin, X.; Zheng, W.; Cao, G.; Sun, Y.; Zhang, Y. Spent lead-acid battery recycling in China–A review and sustainable analyses on mass flow of lead. Waste Manag. 2017, 64, 190–201. [Google Scholar] [CrossRef] [PubMed]
Ellis, T.W.; Mirza, A.H. The refining of secondary lead for use in advanced lead-acid batteries. J. Power Sources 2010, 195, 4525–4529. [Google Scholar] [CrossRef]
Bernardes, A.M.; Espinosa, D.C.R.; Tenorio, J.A.S. Recycling of batteries: A review of current processes and technologies. J. Power Sources 2004, 130, 291–298. [Google Scholar] [CrossRef]
Zhu, X.; Yang, J.; Gao, L.; Liu, J.; Yang, D.; Sun, X.; Zhang, W.; Wang, Q.; Li, L.; He, D.; et al. Preparation of lead carbonate from spent lead paste via chemical conversion. Hydrometallurgy 2013, 134–135, 47–53. [Google Scholar] [CrossRef]
Andrews, D.; Raychaudhuri, A.; Frias, C. Environmentally sound technologies for recycling secondary lead. J. Power Sources 2000, 88, 124–129. [Google Scholar] [CrossRef]
Liu, W.; Tian, J.; Chen, L.; Guo, Y. Temporal and spatial characteristics of lead emissions from the lead-acid battery manufacturing industry in China. Environ. Pollut. 2017, 220, 696–703. [Google Scholar] [CrossRef]
Spanos, C.; Berlinger, S.A.; Jayan, A.; West, A.C. Inverse Charging Techniques for Sulfation Reversal in Flooded Lead-Acid Batteries. J. Electrochem. Soc. 2016, 163, A1612–A1618. [Google Scholar] [CrossRef]
Jolly, R.; Rhin, C. The recycling of lead-acid batteries: Production of lead and polypropylene. Resour. Conserv. Recycl. 1994, 10, 137–143. [Google Scholar] [CrossRef]
Rust, N.; Ferg, E.E.; Masalova, I. A degradation study of isotactic virgin and recycled polypropylene used in lead acid battery casings. Polym. Test. 2006, 25, 130–139. [Google Scholar] [CrossRef]
Hong, S.; Cannon, F.S.; Hou, P.; Byrne, T.; Nieto-Delgado, C. Adsorptive removal of sulfate from acid mine drainage by polypyrrole modified activated carbons: Effects of polypyrrole deposition protocols and activated carbon source. Chemosphere 2017, 184, 429–437. [Google Scholar] [CrossRef] [PubMed]
Cuesta Mayorga, I.; Astilleros, J.M.; Fernández-Díaz, L. Precipitation of CaCO₃ polymorphs from aqueous solutions: The role of pH and sulfate groups. Minerals 2019, 9, 178. [Google Scholar] [CrossRef]
Gominsek, T.; Lubej, A.; Pohar, C. Continuous precipitation of calcium sulfate dehydrate from waste sulfuric acid and lime. J. Chem. Technol. Biotechnol. 2005, 80, 939–947. [Google Scholar] [CrossRef]
Najib, T.; Solgi, M.; Farazmand, A.; Heydarian, S.M.; Nasernejad, B. Optimization of sulfate removal by sulfate reducing bacteria using response surface methodology and heavy metal removal in a sulfidogenic UASB reactor. J. Environ. Chem. Eng. 2017, 5, 3256–3265. [Google Scholar] [CrossRef]
Arahman, N.; Mulyati, S.; Lubis, M.R.; Takagi, R.; Matsuyama, H. Removal profile of sulfate ion from mix ion solution with different type and configuration of anion exchange membrane in electrodialysis. J. Water Process Eng. 2017, 20, 173–179. [Google Scholar] [CrossRef]
Kartic, D.N.; Narayana, B.C.H.A.; Arivazhagan, M. Removal of high concentration of sulfate from pigment industry effluent by chemical precipitation using barium chloride: RSM and ANN modeling approach. J. Environ. Manag. 2018, 206, 69–76. [Google Scholar] [CrossRef]
Fang, P.; Tang, Z.; Chen, X.; Huang, J.; Tang, Z.; Cen, C. Removal of High-Concentration Sulfate Ions from the Sodium Alkali FGD Wastewater Using Ettringite Precipitation Method: Factor Assessment, Feasibility, and Prospect. J. Chem. 2018, 2018, 1265168. [Google Scholar] [CrossRef]
Garrels, R.M.; Thompson, M.E. A chemical model for sea water at 25 degrees C and one atmosphere total pressure. Am. J. Sci. 1962, 260, 57–66. [Google Scholar] [CrossRef]
Helgeson, H.C.; Kirkham, D.H.; Flowers, G.C. Theoretical prediction of the thermodynamic behavior of aqueous electrolytes by high pressures and temperatures; IV, Calculation of activity coefficients, osmotic coefficients, and apparent molal and standard and relative partial molal properties to 600 degrees C and 5kb. Am. J. Sci. 1981, 281, 1249–1516. [Google Scholar]
Oelkers, E.H.; Helgeson, H.C. Triple-ion anions and polynuclear complexing in supercritical electrolyte solutions. Geochim. Cosmochim. Acta 1990, 54, 727–738. [Google Scholar] [CrossRef]
Shock, E.L.; Oelkers, E.H.; Johnson, J.W.; Sverjensky, D.A.; Helgeson, H.C. Calculation of the thermodynamic properties of aqueous species at high pressures and temperatures. Effective electrostatic radii, dissociation constants and standard partial molal properties to 1000 °C and 5 kbar. J. Chem. Soc. Faraday Trans. 1992, 88, 803–826. [Google Scholar] [CrossRef]
Karimi, H. Effect of pH and initial Pb(II) concentration on the lead removal efficiency from industrial wastewater using Ca(OH)₂. Int. J. Water Wastewater Treat. 2017, 3, 1–4. [Google Scholar]

Figure 1. Calculated species distributions of 30 mM Ca(OH)₂ at different pH: (a) with log concentration vs. pH; (b) with fraction of calcium vs. pH.

Figure 2. Calculated species distributions of 10 mM CaCO₃ at different pH: (a) with log concentration vs. pH; (b) with fraction of calcium vs. pH.

Figure 3. Calculated species distributions of 20 mM CaSO₄ at different pH: (a) with log concentration vs. pH; (b) with fraction of calcium vs. pH; (c) with fraction of sulfate vs. pH.

Figure 4. Calculated species distributions of 1.53 M SO₄²⁻ reacting with 1.55 M Ca(OH)₂ at different pH: (a) with log concentration vs. pH; (b) with fraction of sulfate vs. pH; (c) with fraction of calcium vs. pH.

Figure 5. Calculated species distributions of 8.67 mM SO₄²⁻ reacting with 0.0145 mM Pb²⁺ at different pH: (a) with log concentration vs. pH; (b) with fraction of lead vs. pH.

Figure 6. Calculated species distributions of carbonation process with filtration at different pH: (a) with log concentration vs. pH; (b) with fraction of calcium vs. pH; and (c) with fraction of sulfate vs. pH.

Figure 7. Calculated species distributions of carbonation process without filtration at different pH: (a) C_CO₂ = 0.1 M with log concentration vs. pH; (b) C_CO₂ = 0.1 M with fraction of sulfate vs. pH; (c) C_CO₂ = 1 M with fraction of sulfate vs. pH; and (d) C_CO₂ = 2 M with fraction of sulfate vs. pH.

Figure 8. Calculated lead related species distributions of carbonation process with filtration at different pH: (a) C_CO₂ = 0.1 M with log concentration vs. pH; and (b) C_CO₂ = 0.1 M with fraction of lead vs. pH.

Table 1. Chemicals, formulas, reactions, and equilibrium constants used in the thermodynamic calculations.

Formulas	Possible Chemical Reactions		Log₁₀(K) ¹
H⁺/OH^-	H₂O $\leftrightarrow$ H⁺ + OH⁻	(1)	−13.99
Ca²⁺	2H⁺ + Ca(OH)₂(s) $\leftrightarrow$ Ca²⁺ + 2H₂O	(2)	22.62
CaOH⁺	H⁺ + Ca(OH)₂(s) $\leftrightarrow$ CaOH⁺ + H₂O	(3)	9.785
Ca(OH)₂(s)	CaCO₃(s) + 2H₂O $\leftrightarrow$ 2H⁺ + 2CO₃²⁻ + Ca(OH)₂(s)	(4)	−30.88
CaO(s)	CaCO₃(s) + H₂O $\leftrightarrow$ 2H⁺ + 2CO₃²⁻ + CaO(s)	(5)	−41.0
CaCO₃	CaCO₃(s) $\leftrightarrow$ CaCO₃	(6)	−4.961
CaHCO₃⁺	CaCO₃(s) + H⁺ $\leftrightarrow$ CaHCO₃⁺	(7)	3.08
CaOH⁺	CaCO₃(s) + H₂O $\leftrightarrow$ H⁺ + 2CO₃²⁻ + CaOH⁺	(8)	−21.11
CO₂	2H⁺ + CO₃²⁻ $\leftrightarrow$ H₂O + CO₂	(9)	16.68
CO₂(g)	2H⁺ + CO₃²⁻ $\leftrightarrow$ H₂O + CO₂(g)	(10)	18.15
H₂CO₃	2H⁺ + CO₃²⁻ $\leftrightarrow$ H₂CO₃	(11)	16.70
HCO₃⁻	H⁺ + CO₃²⁻ $\leftrightarrow$ HCO₃⁻	(12)	10.33
Ca²⁺	CaCO₃(s) $\leftrightarrow$ Ca²⁺ + CO₃²⁻	(13)	−8.30
CaOH⁺	CaSO₄(s) + H₂O $\leftrightarrow$ CaOH⁺ + H⁺ + SO₄²⁻	(14)	−17.21
CaSO₄	CaSO₄(s) $\leftrightarrow$ CaSO₄	(15)	−2.190
Ca²⁺/SO₄²⁻	CaSO₄(s) $\leftrightarrow$ Ca²⁺ + SO₄²⁻	(16)	−4.378
Ca(OH)₂ (s)	CaSO₄(s) +2H₂O $\leftrightarrow$ Ca(OH)₂(s) + 2H⁺ + SO₄²⁻	(17)	−26.99
CaO(s)	CaSO₄(s) +H₂O $\leftrightarrow$ CaO + 2H⁺ + SO₄²⁻	(18)	−37.08
CaSO₄·2H₂O (s)	CaSO₄(s) +2H₂O $\leftrightarrow$ CaSO₄·2H₂O(s)	(19)	0.161
H₂SO₄	2H⁺ + SO₄²⁻ $\leftrightarrow$ H₂SO₄	(20)	0.780
HSO₄⁻	H⁺ + SO₄²⁻ $\leftrightarrow$ HSO₄⁻	(21)	1.982
CaOH⁺	Ca(OH)₂(s) + H⁺ $\leftrightarrow$ H₂O + CaOH⁺	(22)	9.785
CaSO₄	CaSO₄·2H₂O(s) $\leftrightarrow$ CaSO₄ +2H₂O	(23)	−2.351
Ca²⁺	Ca(OH)₂(s) + 2H⁺ $\leftrightarrow$ Ca²⁺ + 2H₂O	(24)	22.62
CaO(s)	Ca(OH)₂(s) $\leftrightarrow$ CaO(s) + H₂O	(25)	−10.09
CaSO₄(s)	CaSO₄·2H₂O(s) $\leftrightarrow$ CaSO₄(s) +2H₂O	(26)	−0.161
H₂SO₄	CaSO₄·2H₂O(s) $\leftrightarrow$ H₂SO₄ + Ca(OH)₂(s)	(27)	−26.37
HSO₄⁻	CaSO₄·2H₂O(s) $\leftrightarrow$ HSO₄⁻ + Ca(OH)₂(s) + H⁺	(28)	−25.17
SO₄²⁻	CaSO₄·2H₂O(s) $\leftrightarrow$ SO₄²⁻ + Ca(OH)₂(s) + 2H⁺	(29)	−13.99
CaCO₃	Ca²⁺ + CO₂ + H₂O $\leftrightarrow$ CaCO₃ + 2H⁺	(30)	22.62
CaHCO₃⁺	Ca²⁺ + CO₂ + H₂O $\leftrightarrow$ CaHCO₃⁺ + H⁺	(31)	9.785
CaOH⁺	Ca²⁺ + H₂O $\leftrightarrow$ CaOH⁺ + H⁺	(32)	−30.88
CaSO₄	Ca²⁺ + SO₄²⁻ $\leftrightarrow$ CaSO₄	(33)	−41.0
CO₂(g)	CO₂ $\leftrightarrow$ CO₂(g)	(34)	−4.961
H₂CO₃	CO₂ + H₂O $\leftrightarrow$ H₂CO₃	(35)	3.080
H₂SO₄	2H⁺ + SO₄²⁻ $\leftrightarrow$ H₂SO₄	(36)	−21.11
HCO₃⁻	CO₂ + H₂O $\leftrightarrow$ H⁺ + HCO₃⁻	(37)	16.68
HSO₄⁻	H⁺ + SO₄²⁻ $\leftrightarrow$ HSO₄⁻	(38)	18.15
CO₃²⁻	CO₂ + H₂O $\leftrightarrow$ 2H⁺ + CO₃²⁻	(39)	16.7
Ca(OH)₂(s)	Ca²⁺ + 2H₂O $\leftrightarrow$ Ca(OH)₂(s) + 2H⁺	(40)	10.33
CaCO₃(s)	Ca²⁺ + 2H₂O + CO₂ $\leftrightarrow$ CaCO₃(s)	(41)	−8.30
CaSO₄(s)	Ca²⁺ + SO₄²⁻ $\leftrightarrow$ CaSO₄(s)	(42)	−17.21
CaSO₄·2H₂O(s)	Ca²⁺ + SO₄²⁻+ 2H₂O $\leftrightarrow$ CaSO₄·2H₂O (s)	(43)	−2.19
CaCO₃	Ca(OH)₂(s) + CO₂ $\leftrightarrow$ CaCO₃ + H₂O	(44)	−4.378
CaHCO₃⁺	Ca(OH)₂(s) + CO₂ + H⁺ $\leftrightarrow$ CaHCO₃⁺ + H₂O	(45)	−26.99
CaOH⁺	Ca(OH)₂(s) + H⁺ $\leftrightarrow$ CaOH⁺+ H₂O	(46)	−37.08
CaCO₃(s)	Ca(OH)₂(s) + CO₂ $\leftrightarrow$ CaCO₃(s) + H₂O	(47)	0.161
Pb(OH)₂	Pb²⁺ + 2H₂O $\leftrightarrow$ Pb(OH)₂ + 2H⁺	(48)	−17.12
Pb(OH)₃⁻	Pb²⁺ + 3H₂O $\leftrightarrow$ Pb(OH)₃⁻ + 3H⁺	(49)	−28.06
Pb₃(OH)₄²⁺	2Pb2+ + 4H₂O $\leftrightarrow$ Pb₃(OH)₄²⁺ + 4 H⁺	(50)	−23.88
PbOH⁺	Pb²⁺ + H₂O $\leftrightarrow$ PbOH⁺ + H⁺	(51)	−7.71
PbSO₄	Pb²⁺ + SO₄²⁻ $\leftrightarrow$ PbSO₄	(52)	2.69
Pb(OH)₂(s)	Pb²⁺ + 2H₂O $\leftrightarrow$ Pb(OH)₂(s) + 2H⁺	(53)	−13.6
PbO(s)	Pb²⁺ + 2H₂O $\leftrightarrow$ PbO(s) + 2H⁺	(54)	−12.9
PbSO₄(s)	Pb²⁺ + SO₄²⁻ $\leftrightarrow$ PbSO₄(s)	(55)	7.79
Pb(CO₃)₂²⁻	Pb²⁺ + 2H₂O + 2CO₂ $\leftrightarrow$ Pb(CO₃)₂²⁻ + 4H⁺	(56)	−23.26
PbCO₃	Pb²⁺ + H₂O + CO₂ $\leftrightarrow$ PbCO₃ + 2H⁺	(57)	−10.08
PbCO₃OH⁻	Pb²⁺ + 2H₂O + 2CO₂ $\leftrightarrow$ PbCO₃OH⁻ + 3H⁺	(58)	−18.48
PbHCO₃⁺	Pb²⁺ + H₂O + CO₂ $\leftrightarrow$ PbHCO₃⁺ + H⁺	(59)	−3.331
Pb₃(CO₃)₂(OH)₂(s)	3Pb²⁺ + 3H₂O + 2CO₂ $\leftrightarrow$ Pb₃(CO₃)₂(OH)₂(s) + 6H⁺	(60)	−13.96
PbCO₃(s)	Pb²⁺ + H₂O + CO₂ $\leftrightarrow$ PbCO₃(s) + 2H⁺	(61)	−3.48

Note: ^1. K data obtained from HSC Chemistry^® 6.0 database.

Table 2. Calculated concentrations of different species in saturated Ca(OH)₂, CaCO₃, and CaSO₄ solutions.

Contents	Species	Concentrations (mM)
Saturated Ca(OH)₂ (30 mM)	Ca(OH)₂ (s)	7.203
	Ca²⁺	19.48
	OH⁻	28.44
	CaOH⁺	3.318
Saturated CaCO₃ (10 mM)	CaCO₃(s)	9.847
	CaCO₃	1.094 × 10⁻²
	CaHCO₃⁺	1.415 × 10⁻⁴
	OH⁻	8.886 × 10⁻²
	Ca²⁺	0.1415
	CO₃²⁻	4.318 × 10⁻²
	HCO₃⁻	9.840 × 10⁻²
	H₂CO₃	2.560 × 10⁻⁵
	CO₂	2.468 × 10⁻⁵
Saturated CaSO₄ (20 mM)	OH⁻	1.212 × 10⁻⁴
	SO₄²⁻	12.03
	CaOH⁺	9.681 × 10⁻⁶
	CaSO₄	4.457
	H₂SO₄	3.236 × 10⁻¹³
	HSO₄⁻	6.279 × 10⁻⁵
	Ca²⁺	12.03
	CaSO₄·2H₂O	3.516

Table 3. Calculated equilibrium species distributions of the precipitation process and carbonation process, with and without filtration.

Contents	Species	Concentrations (mM)	Removal Efficiency of SO₄²⁻/Pb²⁺
1.55 M Ca(OH)₂ + 1.53 M SO₄²⁻	OH⁻	26.53	99.15%
	CaOH⁺	3.605
	CaSO₄	4.457
	Ca²⁺	25.06
	SO₄²⁻	8.668
	CaSO₄·2H₂O	1517
	Pb(OH)₂	3.447 × 10⁻⁴	0
	Pb(OH)₃⁻	1.416 × 10⁻²	0
Carbonation after filtration at pH 7 (0.1 M CO₂)	Ca²⁺	0.4509	99.15%
	SO₄²⁻	13.01
	CaSO₄	0.1118
	HCO₃⁻	57.32
	CaCO₃(s)	32.44
	PbCO₃(s)	1.397 × 10⁻²	96.35%
	PbCO₃	2.512 × 10⁻⁴
	PbHCO₃⁺	1.834 × 10⁻⁴
	Pb(CO₃)₂²⁻	7.332 × 10⁻⁵
Carbonation without filtration at pH 7 (0.1 M CO₂)	CaSO₄	4.457	69.61%
	HCO₃⁻	20.48
	Ca²⁺	4.098
	SO₄²⁻	460.43
	CaCO₃(s)	476.2
	CaSO₄·2H₂O	1065

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Gu, S.; Fu, B.; Fujita, T.; Ahn, J.W. Thermodynamic Simulations for Determining the Recycling Path of a Spent Lead-Acid Battery Electrolyte Sample with Ca(OH)₂. Appl. Sci. 2019, 9, 2262. https://doi.org/10.3390/app9112262

AMA Style

Gu S, Fu B, Fujita T, Ahn JW. Thermodynamic Simulations for Determining the Recycling Path of a Spent Lead-Acid Battery Electrolyte Sample with Ca(OH)₂. Applied Sciences. 2019; 9(11):2262. https://doi.org/10.3390/app9112262

Chicago/Turabian Style

Gu, Shuai, Bitian Fu, Toyohisa Fujita, and Ji Whan Ahn. 2019. "Thermodynamic Simulations for Determining the Recycling Path of a Spent Lead-Acid Battery Electrolyte Sample with Ca(OH)₂" Applied Sciences 9, no. 11: 2262. https://doi.org/10.3390/app9112262

APA Style

Gu, S., Fu, B., Fujita, T., & Ahn, J. W. (2019). Thermodynamic Simulations for Determining the Recycling Path of a Spent Lead-Acid Battery Electrolyte Sample with Ca(OH)₂. Applied Sciences, 9(11), 2262. https://doi.org/10.3390/app9112262

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

Thermodynamic Simulations for Determining the Recycling Path of a Spent Lead-Acid Battery Electrolyte Sample with Ca(OH)₂

Abstract

Featured Application

Abstract

1. Introduction

2. Materials and Methods

2.1. Materials

2.2. Methods

3. Results

3.1. Precipitation

3.2. Carbonation

4. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI