Expert Control Systems for Maximum Power Point Tracking in a Wind Turbine with PMSG: State of the Art
Abstract
:Featured Application
Abstract
1. Introduction
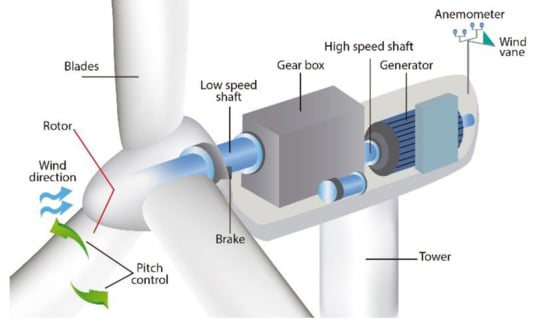
2. Wind Turbine Generator Systems
3. Expert Systems
3.1. Fuzzy Logic
3.2. Artificial Neural Networks
3.3. Intelligent Search Algorithms
4. Results: MPPT Techniques Review
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Court, V. Energy capture, technological change, and economic growth: An evolutionary perspective. BioPhys. Econ. Resour. Qual. 2018, 3, 1–27. [Google Scholar] [CrossRef]
- Sawyer, S.; Dyrholm, M. Global Wind Report Annual Market Update 2017; GWEC Global Wind Energy Council: Brussels, Belgium, 2018. [Google Scholar]
- Wang, L.; Liu, X.; Kolios, A. State of the art in the aeroelasticity of wind turbine blades: Aeroelastic modelling. Renew. Sustain. Energy Rev. 2016, 64, 195–210. [Google Scholar] [CrossRef] [Green Version]
- González-González, A.; Jimenez-Cortadi, A.; Galar, D.; Ciani, L. Condition monitoring of wind turbine pitch controller: A maintenance approach. Measurement 2018, 123, 80–93. [Google Scholar] [CrossRef]
- HMI Vestas Offshore Wind A/S, Dusager 4, 8200 Aarhus N, Denmark Aarhus. Available online: http://www.mhivestasoffshore.com/mhi-vestas-launches -the-first-10-mw-wind-turbine-in-history (accessed on 25 September 2018).
- Bibave, R.; Kulkarni, V. A novel maximum power point tracking method for wind energy conversion system: A review. In Proceedings of the International Conference on Computation of Power, Energy, Information and Communication (ICCPEIC), Chennai, India, 28–29 March 2018. [Google Scholar]
- Novaes-Menezes, E.J.; Araújo, A.M.; da Silva, N.S.B. A review on wind turbine control and its associated methods. J. Clean. Prod. 2018, 174, 945–953. [Google Scholar] [CrossRef]
- Slah, H.; Mehdi, D.; Lassaad, S. Advanced control of a PMSG wind turbine. Int. J. Mod. Nonlinear Theory Appl. 2016, 5, 1–10. [Google Scholar] [CrossRef]
- Amulya, M.; Prashanth, C.; Vijaya, M. Controlling flicker caused due to power fluctuations by using individual pitch control for a variable speed DFIG based wind turbine. Int. Res. J. Eng. Technol. 2017, 4, 286–293. [Google Scholar]
- Tiwari, R.; Babu, N.R. Recent developments of control strategies for wind energy conversion system. Renew. Sustain. Energy Rev. 2016, 66, 268–285. [Google Scholar] [CrossRef]
- Soued, S.; Ebrahim, M.A.; Ramadan, H.S.; Becherif, M. Optimal blade pitch control for enhancing the dynamic performance of wind power plants via metaheuristic optimizers. IET Electr. Power Appl. 2017, 11, 1432–1440. [Google Scholar] [CrossRef]
- Asghar, A.B.; Liu, X. Estimation of wind turbine power coefficient by adaptive neuro-fuzzy methodology. Neurocomputing 2017, 238, 227–233. [Google Scholar] [CrossRef]
- Karthi, K.; Radhakrishnan, R.; Baskaran, J.; Sam-Titus, L. A review of maximum power point tracking controls and wind electric generators. In Proceedings of the International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 11–12 July 2018. [Google Scholar]
- Abdullah, M.A.; Yatim, A.H.M.; Tan, C.W.; Saidur, R. A review of maximum power point tracking algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2012, 16, 3220–3227. [Google Scholar] [CrossRef]
- Kumar, D.; Chatterjee, K. A review of conventional and advanced MPPT algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2016, 1, 957–970. [Google Scholar] [CrossRef]
- Amrouche, S.; Rekioua, D.; Rekioua, T.; Bacha, S. Overview of energy storage in renewable energy systems. Int. J. Hydrog. Energy 2016, 41, 20914–20927. [Google Scholar] [CrossRef]
- Chavero-Navarrete, E.; Perea, M.T.; Correa, J.C.J.; Serrano, R.V.C.; Moreno, G.J.R. Expert control systems implemented in a pitch control of wind turbine: A review. IEEE Access 2019, 7, 13241–13259. [Google Scholar] [CrossRef]
- Hansen, A.D. Wind Turbine Technologies. In Wind Energy Engineering, 1st ed.; Elsevier Inc.: Roskilde, Denmark, 2017; pp. 145–160. [Google Scholar]
- Eisa, S.A. Modeling Dynamics and Control of type-3 DFIG wind turbines: Stability, Q Droop Function, Control Limits and Extreme Scenarios Simulations. Electr. Power Syst. Res. 2019, 166, 29–42. [Google Scholar] [CrossRef]
- Eisa, S.A.; Stone, W.; Wedeward, K. Mathematical modeling, stability, bifurcation analysis and simulations of a type-3 DFIG wind turbine’s dynamics with pitch control. In Proceedings of the 2017 Ninth Annual IEEE Green Technologies Conference (Green Tech), Denver, CO, USA, 21 April 2017. [Google Scholar]
- Eisa, S.A.; Wedeward, K.; Stone, W. Sensitivity analysis of a type-3 DFAG wind turbine’s dynamics with pitch control. In Proceedings of the 2016 IEEE Green Energy and Systems Conference (IGESC), Long Beach, CA, USA, 7 November 2016. [Google Scholar]
- Eisa, S.A.; Wedeward, K.; Stone, W. Wind Turbines Control Systems: Nonlinear Modeling, Simulation, two and three time scale approximations, and data validation. Int. J. Dyn. Control 2018, 6, 1776–1798. [Google Scholar] [CrossRef]
- Eisa, S.A. Nonlinear modeling, analysis and simulation of wind turbine control system with and without pitch control as in industry. In Advanced Control and Optimization Paradigms for Wind Energy Systems; Springer: Paris, France, 2019; pp. 1–40. [Google Scholar]
- Muyeen, S.M.; Hasan-Ali, M.; Takahashi, R.; Murata, T.; Tamura, J.; Tomaki, Y.; Sasano, E. Comparative study on transient stability analysis of wind turbine generator system using different drive train models. IET Renew. Power Gener. 2007, 1, 131–141. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Zhang, Y.; Chen, J.; Sang, Y.; Jiang, L. Passivity-based sliding-mode control design for optimal power extraction of a PMSG based variable speed wind turbine. Renew. Energy 2018, 119, 577–589. [Google Scholar] [CrossRef]
- Liu, J. Intelligent Control Design and MatLab Simulation, 1st ed.; Tsinghua University Press: Beijing, China, 2018. [Google Scholar]
- Chamorro, H.R.; Riaño, I.; Gerndt, R.; Zelinka, I.; Gonzalez-Longatt, F.; Sood, V.K. Synthetic inertia control based on fuzzy adaptive differential evolution. Int. J. Electr. Power Energy Syst. 2019, 105, 803–813. [Google Scholar] [CrossRef]
- Elfergani, A.; Elsharif, M.A.A.; Hamd, R.H.A.; Saad, S.M.; Naily, N.E.; Mohamed, F.A. Advanced self-tuned pitch angle control based on fuzzy logic for grid connected variable-speed wind turbine system. In Proceedings of the IEEE 9th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 20–22 March 2018. [Google Scholar]
- Ayrir, W.; Ourahou, M.; El-Hassouni, B.; Haddi, A. Direct torque control improvement of a variable speed DFIG based on a fuzzy inference system. Math. Comput. Simul. 2018. [Google Scholar] [CrossRef]
- Mazouz, F.; Belkacem, S.; Ouchen, S.; Harbouche, Y.; Abdessemed, R. Fuzzy Control of a Wind System Based on the DFIG; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2018; pp. 173–181. [Google Scholar]
- Da-Silva, I.N.; Spatti, D.; Andrade, R.; Bartocci, L.H.; Dos-Reis, S.F. Artificial Neural Networks: A Practical Course, 1st ed.; Springer International Publishing: New York, NY, USA, 2017. [Google Scholar]
- Zgurovsky, M.Z.; Zaychenko, Y.P. The Fundamentals of Computational Intelligence: System Approach, 1st ed.; Springer International Publishing: New York, NY, USA, 2017. [Google Scholar]
- Marugán, A.P.; Márquez, F.P.G.; Perez, J.M.P.; Ruiz-Hernández, D. A survey of artificial neural network in wind energy systems. Appl. Energy 2018, 228, 1822–1836. [Google Scholar] [CrossRef] [Green Version]
- Couceiro, M.; Ghamisi, P. Fractional Order Darwinian Particle Swarm Optimization, Applications and Evaluation of an Evolutionary Algorithm, 1st ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Kiranyaz, S.; Ince, T.; Gabbouj, M. Multidimensional Particle Swarm Optimization for Machine Learning and Pattern Recognition, 1st ed.; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Kesraoui, M.; Lagraf, S.A.; Chaib, A. Aerodynamic power control of wind turbine using fuzzy logic. In Proceedings of the IEEE 3rd International Renewable and Sustainable Energy Conference (IRSEC), Marrakech & Ouarzazate, Marrakech, Morocco, 10–13 December 2015. [Google Scholar]
- Ben-Smida, M.; Sakly, A. Fuzzy pitch angle control for grid connected variable-speed wind turbine system. In Proceedings of the IEEE 7th International Renewable Energy Congress, Hammamet, Tunisia, 22–24 March 2016. [Google Scholar]
- Slimen, A.; Tlijani, H.; Dhaoui, M.; Younes, R.B. Intelligent control of wind pump based on PMSG using pitch control. In Proceedings of the IEEE 14th International Multi-Conference on Systems, Signals & Devices (SSD), Marrakech Tensift El Haouz, Marrakech, Marocco, 30 March 2017. [Google Scholar]
- Al-Toma, A.S.; Taylor, G.A.; Abbod, M. Intelligent pitch angle control scheme for variable speed wind generator systems. In Proceedings of the IEEE 52nd International Universities Power Engineering Conference (UPEC), Crete, Greece, 28–31 August 2017. [Google Scholar]
- Narasimalu, S.; Chellaiah, B. Pitch angle control for horizontal axis wind turbine: A comparative study. In Proceedings of the IEEE Asian Conference on Energy, Power and Transportation Electrification (ACEPT), Singapore, 24–26 October 2017. [Google Scholar]
- Marmouh, S.; Boutoubat, M.; Mokrani, L. MPPT fuzzy logic controller of a wind energy conversion system based on a PMSG. In Proceedings of the 8th International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 15–17 November 2016. [Google Scholar]
- Rajvikram, M.; Renuga, P.; Swathisriranjani, M. Fuzzy based MPPT controller’s role in extraction of maximum power in wind energy conversion system. In Proceedings of the International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT), Medea, Algeria, 16–17 December 2016. [Google Scholar]
- Zheng, X.; Ding, D.; Li, P. Power Stable Regulation of Direct-Drive Permanent Magnet Wind. Power System Using Pitch and Torque Control; Electrical Engineering Department, Harbin Institute of Technology: Harbin, China, 2015. [Google Scholar]
- Cholo, C.A.; Ruiz, J.A.; Guacaneme, J.A. Evaluation of MPPT methods using fuzzy logic applied to a low power wind turbine. In Proceedings of the IEEE Workshop on Power Electronics and Power Quality Applications (PEPQA), Bogota, Colombia, 31 May–2 June 2017. [Google Scholar]
- Pachauri, R.K.; Kumar, H.; Gupta, A.; Chauhan, Y.K. Pitch Angle Controlling of Wind Turbine System Using Proportional-Integral/Fuzzy Logic Controller. Smart Innovation, Systems and Technologies; Springer: New Delhi, India, 2016; pp. 55–63. [Google Scholar]
- Tiwari, R.; Ramesh, N.; Sanjeevikumar, P. Fuzzy Logic-Based Pitch Angle Controller for PMSG-Based Wind Energy Conversion System. Advances in Smart Grid and Renewable Energy; Springer: Singapore, 2017; pp. 277–286. [Google Scholar]
- Van, T.L.; Nguyen, T.H.; Lee, D.C. Advanced pitch angle control based on fuzzy logic for variable-speed wind turbine systems. IEEE Trans. Energy Convers. 2015, 30, 578–587. [Google Scholar] [CrossRef]
- Yang, J.; Song, D.; Han, H.; Tong, P.; Zhou, L. The integrated control of fuzzy logic and model-based approach for variable-speed wind turbine. Turk. J. Electr. Eng. Comput. Sci. 2015, 23, 1715–1734. [Google Scholar] [CrossRef]
- Vega, D.C.; Marin, J.A.; Sanchez, R.T. Pitch angle controllers design for a horizontal axis wind turbine. In Proceedings of the IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa and Zihuatanejo, Ixtapa, Mexico, 4–6 November 2015. [Google Scholar]
- Huang, J.; Jia, H.; Cheng, G. Fuzzy-PI and fuzzy feedforward compound control of variable pitch system. In Proceedings of the 36th Chinese Control Conference, Dalian, China, 26–28 July 2017. [Google Scholar]
- Civelek, Z.; Lüy, M.; Çam, E.; Barışçı, N. Control of Pitch Angle of Wind Turbine by Fuzzy PID Controller. Intell. Autom. Soft Comput. 2016, 22, 463–471. [Google Scholar] [CrossRef]
- Alarcon, O.F.; Velasquez, B.I.; Hunter, A.R.; Pavez, L.B.; Moncada, R. Hybrid PID-fuzzy pitch control for wind turbines. In Proceedings of the IEEE Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Pucon, Chile, 18–20 October 2017. [Google Scholar]
- Baburajan, S. Improving the efficiency of a wind turbine system using a fuzzy-pid controller. In Proceedings of the IEEE Advances in Science and Engineering Technology International Conferences (ASET), Dubai and Sharjah and Abu Dhabi, Abu Dhabi, United Arab Emirates, 6 February–5 April 2018. [Google Scholar]
- Aicha, A.; Youcef, M.; Said, H.; Tayeb, A. Intelligent maximum power tracking control of PMSG wind energy conversion system. In Proceedings of the 5th International Conference on Electrical Engineering—Boumerdes (ICEE-B), Boumerdes, Algeria, 29–31 October 2017. [Google Scholar]
- Xiao, Y.; Huo, W.; Nan, G. Study of variable pitch control for direct-drive permanent magnet wind Turbines based on fuzzy logic algorithm. J. Inf. Comput. Sci. 2015, 12, 2849–2856. [Google Scholar] [CrossRef]
- Beddar, A.; Bouzekri, H.; Babes, B.; Afghoul, H. Experimental enhancement of fuzzy fractional order PI+I controller of grid connected variable speed wind energy conversion system. Energy Convers. Manag. 2016, 123, 569–580. [Google Scholar] [CrossRef]
- Elyaalaoui, K.; Ouassaid, M.; Cherkaoui, M. Primary frequency control using hierarchal fuzzy logic for a wind farm based on SCIG connected to electrical network. Sustain. Energy Grids Netw. 2018, 16, 188–195. [Google Scholar] [CrossRef]
- Ponce, P.; Ponce, H.; Molina, A. Doubly fed induction generator DFIG wind turbine controlled by artificial organic networks. Soft Comput. 2017, 22, 2867–2879. [Google Scholar] [CrossRef]
- Lee, J.; Kim, Y.S. Sensorless fuzzy-logic-based maximum power point tracking control for a small-scale wind power generation systems with a switched-mode rectifier. IET Renew. Power Gener. 2016, 10, 194–202. [Google Scholar] [CrossRef]
- Civelek, Z.; Lüy, M.; Çam, E.; Mamur, H. A new fuzzy logic proportional controller approach applied to individual pitch angle for wind turbine load mitigation. Renew. Energy 2017, 111, 708–717. [Google Scholar] [CrossRef]
- Han, B.; Yang, F.; Xiang, Z.; Zhou, L. Individual pitch controller based on fuzzy logic control for wind turbine load mitigation. IET Renew. Power Gener. 2016, 10, 687–693. [Google Scholar] [CrossRef]
- Lasheen, A.; Elshafei, L. Wind turbine collective pitch control via a fuzzy predictive algorithm. Renew. Energy 2016, 87, 298–306. [Google Scholar] [CrossRef]
- Yin, X.; Lin, Y.; Li, W.; Gu, Y.; Liu, H.; Lei, P. A novel fuzzy integral sliding mode current control strategy for maximizing wind power extraction and eliminating voltage harmonics. Energy 2015, 85, 677–686. [Google Scholar] [CrossRef]
- Saad, L.; Hicham, H.; Khalid, F. Optimal tracking, modeling and control of aerogenerator based on PMSG driven by wind turbine. In Proceedings of the IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, UK, 20–23 November 2016. [Google Scholar]
- Thanh, S.N.; Xuan, H.H.; The, C.N.; Hung, P.P.; Van, T.P.; Kennel, R. Fuzzy logic based maximum power point tracking technique for a stand-alone wind energy system. In Proceedings of the IEEE International Conference on Sustainable Energy Technologies (ICSET), Hanoi, Vietnam, 14–16 November 2016. [Google Scholar]
- Yin, X.; Zhang, W. Recurrent neural network based adaptive integral sliding mode power maximization control for wind power systems. Renew. Energy 2019. [Google Scholar] [CrossRef]
- Hong, C.M.; Chen, C.H.; Tu, C.S. Maximum power point tracking-based control algorithm for PMSG wind generation system without mechanical sensors. Energy Convers. Manag. 2013, 69, 58–67. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Liu, Y. Implementation of maximum power point tracking based on variable speed forecasting for wind energy systems. Processes 2019, 7, 158. [Google Scholar] [CrossRef]
- Jiao, X.; Meng, W.; Yang, Q.; Fu, L.; Chen, Q. Adaptive continuous neural pitch angle control for variable-speed wind turbines. Asian J. Control 2019. [Google Scholar] [CrossRef]
- Tiwari, R.; Krishnamurthy, K.; Neelakandan, R.; Padmanaban, S.; Wheeler, P. Neural network based maximum power point tracking control with quadratic boost converter for PMSG—Wind energy conversion system. Electronics 2018, 7, 20. [Google Scholar] [CrossRef]
- Tiwari, R.; Padmanaban, S.; Neelakandan, R. Coordinated control strategies for a permanent magnet synchronous generator based wind energy conversion system. Energies 2017, 10, 1493. [Google Scholar] [CrossRef]
- Heshmatian, S.; Khosravi, M.; Khaburi, D.A.; Rivera, M. A wind speed sensorless MPPT-pitch angle control scheme for a WECS using integral sliding mode control and neural network. In Proceedings of the IEEE Southern Power Electronics Conference (SPEC), Puerto Varas, Chile, 4–7 December 2017. [Google Scholar]
- Roodsari, B.N.; Macnab, C.J.B.; Nowicki, E.P. A novel adaptive controller using radial basis function neural network for the wind energy conversion system. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017. [Google Scholar]
- Mjabber, E.K.E.; Hajjaji, A.E.; Khamlichi, A. Analysis of a RBF neural network based controller for pitch angle of variable-speed wind turbines. Procedia Eng. 2017, 181, 552–559. [Google Scholar] [CrossRef]
- Han, B.; Zhou, L.; Zhang, Z. LIDAR-assisted radial basis function neural network optimization for wind turbines. IEEJ Trans. Electr. Electron. Eng. 2017, 13, 195–200. [Google Scholar] [CrossRef]
- Rahman, M.M.A.; Rahim, A.H.M.A. Performance evaluation of ANN and ANFIS based wind speed sensor-less MPPT controller. In Proceedings of the 5th International Conference on Informatics, Electronics and Vision (ICIEV), Dhaka, Bangladesh, 13–14 May 2016. [Google Scholar]
- Wei, C.; Zhang, Z.; Qiao, W.; Qu, L. An adaptive network-based reinforcement learning method for MPPT control of PMSG wind energy conversion systems. IEEE Trans. Power Electron. 2016, 31, 7837–7848. [Google Scholar] [CrossRef]
- Bagheri, P.; Sun, Q. Adaptive robust control of a class of non-affine variable-speed variable-pitch wind turbines with unmodeled dynamics. ISA Trans. 2016, 63, 233–241. [Google Scholar] [CrossRef] [PubMed]
- Dahbi, A.; Nait-Said, N.; Nait-Said, M.S. A novel combined MPPT-pitch angle control for wide range variable speed wind turbine based on neural network. Int. J. Hydrog. Energy 2016, 41, 9427–9442. [Google Scholar] [CrossRef]
- Kang, J.; Meng, W.; Abraham, A.; Liu, H. An adaptive PID neural network for complex nonlinear system control. Neurocomputing 2014, 135, 79–85. [Google Scholar] [CrossRef]
- Assareh, E.; Biglari, M. A novel approach to capture the maximum power from variable speed wind turbines using PI controller, RBF neural network and GSA evolutionary algorithm. Renew. Sustain. Energy Rev. 2015, 51, 1023–1037. [Google Scholar] [CrossRef]
- Wu, S.; Wang, Y.; Cheng, S. Extreme learning machine based wind speed estimation and sensorless control for wind turbine power generation system. Neurocomputing 2013, 102, 163–175. [Google Scholar] [CrossRef]
- Mohamed, A.A.A.; Haridy, A.L.; Hemeida, A.M. The whale optimization algorithm based controller for PMSG wind energy generation system. In Proceedings of the International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019. [Google Scholar]
- Priyadarshi, N.; Ramachandaramurthy, V.; Padmanaban, S.; Azam, F. An ant colony optimized MPPT for standalone hybrid PV-wind power system with single Cuk converter. Energies 2019, 12, 167. [Google Scholar] [CrossRef]
- Saad, N.H.; El-Sattar, A.A.; Marei, M.E. Improved bacterial foraging optimization for grid connected wind energy conversion system based PMSG with matrix converter. Ain Shams Eng. J. 2018, 9, 2183–2193. [Google Scholar] [CrossRef]
- Civelek, Z.; Çam, E.; Lüy, M.; Mamur, H. Proportional integral derivative parameter optimization of blade pitch controller in wind turbines by a new intelligent genetic algorithm. IET Renew. Power Gener. 2016, 10, 1220–1228. [Google Scholar] [CrossRef]
- Ebrahim, M.A.; Becherif, M.; Abdelaziz, A.Y. Dynamic performance enhancement for wind energy conversion system using Moth-Flame Optimization based blade pitch controller. Sustain. Energy Technol. Assess. 2018, 27, 206–212. [Google Scholar] [CrossRef]
- Kim, M.K. Optimal control and operation strategy for wind turbines contributing to grid primary frequency regulation. Appl. Sci. 2017, 7, 927. [Google Scholar] [CrossRef]
- Daud Pribadi, K.; Danang Wijaya, F. Sarjiya Dynamic response of maximum power point tracking using particle swarm optimization for wind energy conversion system. In Proceedings of the 8th International Conference on Information Technology and Electrical Engineering (ICITEE), Yogyakarta, Indonesia, 5–6 October 2016. [Google Scholar]
- Yassin, H.M.; Hanafy, H.H.; Hallouda, M.M. Design and implementation of PI controllers of direct drive PMSG wind turbine system tuned by Linearized biogeography-based optimization technique. In Proceedings of the 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016. [Google Scholar]
- Behera, S.; Subudhi, B.; Bhusan, B. Design of PI controller in pitch control of wind turbine: A comparison of PSO and PS algorithm. Int. J. Renew. Energy Res. 2016, 6, 271–281. [Google Scholar]
- Hodzic, M.; Tai, L.C. Grey predictor reference model for assisting particle swarm optimization for wind turbine control. Renew. Energy 2016, 86, 251–256. [Google Scholar] [CrossRef]
- Kasiri, H.; Momeni, H.R.; Abadeh, M.S. Review and improvement of several optimal intelligent pitch controllers and estimator of WECS via artificial intelligent approaches. In Complex System Modelling and Control Through Intelligent Soft Computations, 1st ed.; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Taher, S.A.; Farshadnia, M.; Mozdianfard, M.R. Optimal gain scheduling controller design of a pitch-controlled VS-WECS using DE optimization algorithm. Appl. Soft Comput. 2013, 13, 2215–2223. [Google Scholar] [CrossRef]




















| i | j | αi,j | i | j | αi,j |
|---|---|---|---|---|---|
| 4 | 4 | 4.9686 × 10−10 | 4 | 3 | −7.1535 × 10−8 |
| 4 | 2 | 1.6167 × 10−6 | 4 | 1 | −9.4839 × 10−6 |
| 4 | 0 | 1.4787 × 10−5 | 3 | 4 | −8.9194 × 10−8 |
| 3 | 3 | 5.9924 × 10−6 | 3 | 2 | −1.0479 × 10−4 |
| 3 | 1 | 5.7051 × 10−4 | 3 | 0 | −8.6018 × 10−4 |
| 2 | 4 | 2.7937 × 10−6 | 2 | 3 | −1.4855 × 10−4 |
| 2 | 2 | 2.1495 × 10−3 | 2 | 1 | −1.0996 × 10−2 |
| 2 | 0 | 1.5727 × 10−2 | - | - | - |
| 1 | 4 | −2.3895 × 10−5 | 1 | 3 | 1.0683 × 10−3 |
| 1 | 2 | −1.3365 × 10−4 | 1 | 1 | 6.0405 × 10−2 |
| 1 | 0 | −6.7606 × 10−2 | 0 | 4 | 1.1524 × 10−5 |
| 0 | 3 | −1.3365 × 10−4 | 0 | 2 | −1.2406 × 10−2 |
| 0 | 1 | 2.1808 × 10−1 | 0 | 0 | −4.1909 × 10−1 |
| Reference | Analysis of Results |
|---|---|
| Tiwari et al., 2018 | With a PI controller, the average power is 16.9 kW and generator speed varies. With FLC the average power is 17.2 kW and the generator speed established at 14.2 rad/s. |
| Barburajan, 2018 | Was compared the responses of the Fuzzy-PID and PID controllers. F-PID reduces rise time of 4.21 s to 0.63 s. PID has oscillations with a peak overshoot of 11.8% and F-PID of 0.02%. |
| Elyaalaoui et al., 2018 | Comparing PI, PDFPI and PIFPI controllers, the maximum settling time is 4 s, 4.7 s and 2 s respectively. The deviation (HZ) are −0.06 for IC, −0.04 for PI, −0.045 for PDFPI, and −0.01 for PIFPI. |
| Ponce et al., 2017 | Pitch angle is smaller with PID-AOC (5.2°) than with PID controller (8.2°). Stator and rotor power increase significantly, 10.8 and 30.5%, respectively. PID generates 2.5% of overshooting, while PID-AOC reaches 0.8%, increasing the performance in 68.0%. |
| Alarcaon et al., 2017 | According to error criteria compared between PID, diffuse and Hybrid (F-PID-5) controllers. The F-PID-5 obtained a minor error in the reference change. 66.16% better than FLC basic controller and 2.4% with respect to a PID. |
| Huang et al., 2017 | Results show that generator speed response improves from 3.68 s to 3.28 s on proposed method. Performance is improved in the attenuate oscillations of the actuator and the overshoot of the generator speed has been reduced. |
| Slimen et al., 2017 | Graphic results demonstrated better performance for FLC schemes than a PI control. |
| Al-Toma et al., 2017 | FLC reduces the overshoot by about 10% compared with a PI controller. |
| Aicha et al., 2017 | The adaptive FLC-PI controller shows a good performance and delivers more tracking speed and efficient maximum power tracking under fluctuating wind conditions than PI and fuzzy-PI controllers. |
| Cholo et al., 2017 | A ripple percentage of 2.13% was obtained, 84.28% lower than that of a P&O controller, allowing to affirm that the FLC controller has a better result. |
| Habibi et al., 2016 | It was compared with a proposed PI with better response time of 130 s versus 400 s. Overshoot reduction 1%. |
| Pachauri et al., 2016 | It compared with a PI controller. The settling time are Pitch angle 0.9 s for PI and 0.3 for FLC. Torque 1.0 s for PI and 0.25 s for FLC. Rotor speed 0.95 s for PI and 0.43 s for FLC. And EM torque 0.9 s for PI and 0.3 s for FLC. |
| Smida and Sakly, 2016 | It was compared with a PI control obtaining a better average error of 0.018% to 0.0088%, in absolute values it was reduced from 65.8% to 29.02% |
| Beddar et al., 2016 | The results illustrate the robustness and the superiority of FFOPI+I over FOPI and conventional PI, since guarantee low current total harmonic distortion with small overshot and fast settling time. |
| Civelek et al., 2015 | A PI reached best response time, an error in 1% in 1.5, FLC 3.5 s and FLC-PID in 0.35 s. Maximum Overshoot of the output power was reached to 790kW-PI, 740kW-FLC and 530kW-FLC-PID. |
| Vega et al., 2015 | The proposed combined controller FLC-PI has a better response than the PI controller and the FLC, this has been proved with a lower error of 0.4% compared to 0.66% from the PI and 1.33% from the FLC. |
| Xiao et al., 2015 | According to simulations, the proposed controller provides better performance compared to a PID. Its behavior is better near the nominal wind speed reducing the power overshoot to 3% than the cut-speed with only 0.4%. |
| Yang et al., 2015 | The average power for a conventional controller and the proposed is 2.98 MW and 3.01 MW, respectively. The speed rotor reached by gross controller is 19.7 rpm, higher than speed cut. Proposed controller reaches 19.15 rpm, lower than speed cut. |
| Van et al., 2015 | The average output power simulate in 2 MW PMSG with the proposed methods is 2.36%, 1.07% y 1.5% respectively higher. |
| Reference | Analysis of Results |
|---|---|
| Yin and Zhang, 2019 | Comparative experimental results with [67] demonstrates that the proposed controller possesses a remarkable learning capability of the RNN weights and can be used to maintain the optimum generator power. |
| Zhang et al., 2019 | Results show that the flux linkage and turbine rotational speed tracking the reference value almost without oscillation and back to stable state, which indicates its highly acceptable tracking performance, considering the quick reaction and following-up time. |
| Jiao et al., 2019 | With turbulent wind the standard deviation of generator shaft speed is 0.0206 rad/s for NN controller, and 0.0351 rad/s for the PI counterpart. The NN controller can produce smaller oscillation and provide electrical energy with higher quality for grid integration. |
| Tiwari et al., 2018 | The results are compared with a classical Perturb and Observe (P&O) method. The overall performance comparison of the maximum power drawn was 7.28% greater using the Boost converter, 3.68 with the SEPIC converter and 3.34 with the quadratic increase converter for wind speed below the rated speed. |
| Tiwari et al., 2017 | The proposed controller gives 2.021%, 4.623% and 9.893% more power during below rated wind speed and during above rated wind speed it produces 0.187%, 1.67%, 3.67% and 5.38% of rated generator power than the BPN, FLC and PI controller respectively. |
| Heshmatian et al., 2017 | A comparison is made between MLPNN controller and conventional PI regarding their performance in adjusting the pitch angle. The results approve the designed controller to be much faster and more accurate than the conventional PI. |
| Roodsari et al., 2017 | Compared with a well-designed PID controller the proposed adaptive controller shows less fluctuation in following the desired system power pattern and less rotor speed errors. |
| Mjabber et al., 2017 | Compared with a PI controller. Rotor speed is very stable and its fluctuation are considerably reduced. The pitch angle variations are much lower. The generator torque is very stable, the mean value is only 133.5-kNm than the 139.4 kNm given by PI. |
| Han et al., 2017 | The baseline controller is compared with PI controller. The effectiveness of controller is evaluated based on the damage equivalent loads. The tower base fore–aft moment was reduced by 15.3%, the tower base side-to-side moment was reduced by 9.8%, and the tower base torsional moment was reduced by 10.4%. |
| Rahman et al., 2016 | The performance ANFIS controller is compared with ANN controller. The maximum power error is 0.0095 watts for ANN and 0.000123 watts for ANFIS. |
| Wei et al., 2016 | The proposed algorithm enables the PMSG to produce a total energy of about 8.4 kJ in the two minutes, which is 5% more than 8 kJ energy produced by the PMSG with a conventional P&O method. |
| Bagheri and Sun, 2016 | The simulation results are analyzed alongside a PI controller and the controller designed for Jafarnejadsani et al. (2013). The proposed controller can precisely track the desired rotor speed in second region, but not the other controllers. The tracking error of the proposed controller is lower resulting in a lower generator torque. |
| Dahbi et al., 2016 | Graphic results show good behavior on the optimal rotor speed. Increased efficiency and performance of the turbine. The grid voltages and injected currents are in phase; therefore, unit power factor is reached. |
| Kang et al., 2014 | It was compared between traditional PID, PID-NN though standard PSO and adaptive PID-NN. Was documented the errors varied with time, with a time interval of 0.001 s. The adaptive PID-NN controller has fast convergence speed, high accuracy and stability. |
| Wu et al., 2013 | The proposed ELM wind speed estimation and sensorless control are proved effective. In most of the time, the wind speed error is less than 0.05 m/s. |
| Reference | Analysis of Results |
|---|---|
| Mohamed et al., 2019 | The results show that the dynamic responses for (T, ω, id, iq) by using WOA based controller results have lower overshoot and smaller setting time than other methods. |
| Priyadarshi et al., 2018 | Experimental results reveal that the ACO based MPPT provides seven times faster convergence compared to the PSO algorithm for achievement of MPP and tracking efficiency. |
| Saad et al., 2018 | The proposed control method has a fast, dynamic response by controlling the generator d-axis current to get the maximum active power under normal wind velocities. In addition, the controller proves to have capability and fast transient response under grid fault condition. |
| Civelek et al., 2016 | According to the results, an appreciable improvement of 17% was calculated on power overshoot with intelligent GA respect to classic GA. Furthermore, stability time was 0.79 better, with controller proposed. |
| Ebrahim et al., 2018 | According to simulations, the suggested design can guarantee system stability under increased mechanical torque perturbations and excessive wind speed with controller parameters uncertainties. Thus, the proposed approach succeeded in proving its capability to select the most robust PID controller. |
| Kim, 2017 | The results demonstrate that the proposed strategy can restrict the frequency drop, decrease the disturbances PMSG. |
| Duad et al., 2016 | With the PSO method, the system achieves a new speed of rotor and stabilized in less than 0.1 s. The system also achieves new output power and is stabilized in less than 0.2 s. When compared with wind turbine system without MPPT, there has been an increasing average efficiency of 25%. |
| Yassini et al., 2016 | Simulation and experimental results show that LBBO is a successful optimization technique in control systems for wind turbine system. |
| Behera et al., 2016 | The standard deviation in angular speed of rotor is seen to be low with the proposed PI-PSO controller (0.0338 pu) as compared to the standard P control (0.0384 pu) and without control (0.0482 pu). Similarly, the pitch angle has increased less (5.0911°) as compared to P control (7.0107°). |
| Hodzic and Tai, 2015 | The performance of the PI-PSO controller produces less oscillations in every analyzed case, especially when wind speed is higher. However, the overshoots are bigger and settling times are longer. |
| Kasiri et al., 2015 | Graphic results shown that in below rated wind speed, optimal power is attained by regulating; thus, the pitch angle is kept at a mechanical minimum and rotor speed is controlled in such a way that it is always acquired, akin to MPP tracking. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chavero-Navarrete, E.; Trejo-Perea, M.; Jáuregui-Correa, J.C.; Carrillo-Serrano, R.V.; Ríos-Moreno, J.G. Expert Control Systems for Maximum Power Point Tracking in a Wind Turbine with PMSG: State of the Art. Appl. Sci. 2019, 9, 2469. https://doi.org/10.3390/app9122469
Chavero-Navarrete E, Trejo-Perea M, Jáuregui-Correa JC, Carrillo-Serrano RV, Ríos-Moreno JG. Expert Control Systems for Maximum Power Point Tracking in a Wind Turbine with PMSG: State of the Art. Applied Sciences. 2019; 9(12):2469. https://doi.org/10.3390/app9122469
Chicago/Turabian StyleChavero-Navarrete, Ernesto, Mario Trejo-Perea, Juan Carlos Jáuregui-Correa, Roberto Valentín Carrillo-Serrano, and José Gabriel Ríos-Moreno. 2019. "Expert Control Systems for Maximum Power Point Tracking in a Wind Turbine with PMSG: State of the Art" Applied Sciences 9, no. 12: 2469. https://doi.org/10.3390/app9122469
APA StyleChavero-Navarrete, E., Trejo-Perea, M., Jáuregui-Correa, J. C., Carrillo-Serrano, R. V., & Ríos-Moreno, J. G. (2019). Expert Control Systems for Maximum Power Point Tracking in a Wind Turbine with PMSG: State of the Art. Applied Sciences, 9(12), 2469. https://doi.org/10.3390/app9122469