Short-Term Forecasting of Power Production in a Large-Scale Photovoltaic Plant Based on LSTM
Abstract
:1. Introduction
2. Theoretical Background
2.1. Neural Networks
2.2. Recurrent Neural Networks and Long Short-Term Memory
2.3. Gradient Descent Algorithm
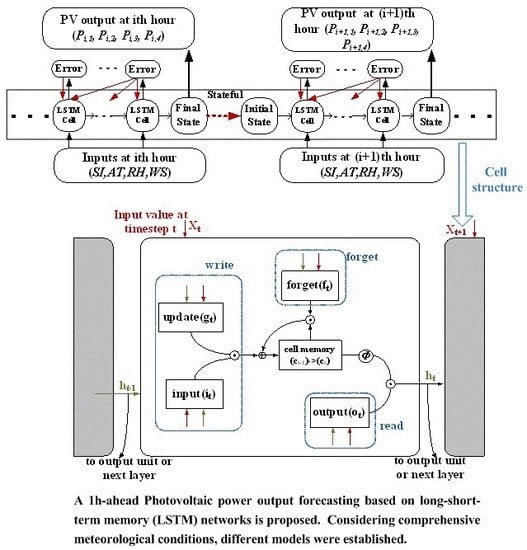
3. Model Description
3.1. Model Structure
3.2. Data Preparation
3.3. Performance Criteria
4. Evaluation and Discussions
4.1. Optimal Model Parameter Selection
4.2. Forecasting Result and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nguyen, T.H.T.; Nakayama, T.; Ishida, M. Optimal capacity design of battery and hydrogen system for the DC grid with photovoltaic power generation based on the rapid estimation of grid dependency. Int. J. Electr. Power Energy Syst. 2017, 89, 27–39. [Google Scholar] [CrossRef]
- Bhatti, A.R.; Salam, Z.; Aziz, M.J.B.A.; Yee, K.P. A critical review of electric vehicle charging using solar photovoltaic. Int. J. Energy Res. 2016, 40, 439–461. [Google Scholar] [CrossRef]
- Carlos, S.; Franco, J.F.; Rider, M.J.; Romero, R. Joint optimal operation of photovoltaic units and electric vehicles in residential networks with storage systems: A dynamic scheduling method. Int. J. Electr. Power Energy Syst. 2018, 103, 136–145. [Google Scholar]
- Miller, E.L.; Gaillard, N.; Kaneshiro, J.; DeAngelis, A.; Garland, R. Progress in new semiconductor materials classes for solar photoelectrolysis. Int. J. Energy Res. 2010, 34, 1215–1222. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M.; Lughi, V. Short-term forecasting of power production in a large-scale photovoltaic plant. Sol. Energy 2014, 105, 401–413. [Google Scholar] [CrossRef]
- Ogliari, E.; Dolara, A.; Manzolini, G.; Leva, S. Physical and hybrid methods comparison for the day ahead PV output power forecast. Renew. Energy 2017, 113, 11–21. [Google Scholar] [CrossRef]
- Vaz, A.; Elsinga, B.; Van Sark, W.; Brito, M. An artificial neural network to assess the impact of neighbouring photovoltaic systems in power forecasting in Utrecht, The Netherlands. Renew. Energy 2016, 85, 631–641. [Google Scholar] [CrossRef]
- Gandoman, F.H.; Aleem, S.H.A.; Omar, N.; Ahmadi, A.; Alenezi, F.Q. Short-term solar power forecasting considering cloud coverage and ambient temperature variation effects. Renew. Energy 2018, 123, 793–805. [Google Scholar] [CrossRef]
- Felice, M.D.; Petitta, M.; Ruti, P.M. Short-term predictability of photovoltaic production over Italy. Renew. Energy 2015, 80, 197–204. [Google Scholar] [CrossRef] [Green Version]
- Nobre, A.M.; Carlos, A.S., Jr.; Karthik, S.; Marek, K.; Zhao, L.; Martins, F.R.; Pereira, E.B.; Rüther, R.; Reindl, T. PV power conversion and short-term forecasting in a tropical, densely-built environment in Singapore. Renew. Energy 2016, 94, 496–509. [Google Scholar] [CrossRef]
- Hoolohan, V.; Tomlin, A.S. Improved near surface wind speed predictions using Gaussian process regression combined with numerical weather predictions and observed meteorological data. Renew. Energy 2018, 126, 1043–1054. [Google Scholar] [CrossRef]
- Huang, R.; Huang, T.; Gadh, R. Solar generation prediciton using the ARMA model in a laboratory-level micro-grid. In Proceedings of the IEEE SmartGridComm 2012 Symposium—Support for Storage, Renewable Sources, and MicroGrid, Tainan, Taiwan, 5–8 November 2012. [Google Scholar]
- Chen, C.; Duan, S.; Cai, T.; Liu, B.; Hu, G. Smart energy management system for optimal microgrid economic operation. IET Renew. Power Gener. 2010, 5, 258–267. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, J.; Xia, J.; Dai, Y.; Sheng, Y.; Yue, J. Performance evaluation and accuracy enhancement of a day-ahead wind power forecasting system in China. Renew. Energy 2012, 43, 234–241. [Google Scholar] [CrossRef]
- Shi, J.; Lee, W.J.; Liu, Y.Q.; Yang, Y.P.; Wang, P. Forecasting Power Output of Photovoltaic Systems Based on Weather Classification and Support Vector Machines. IEEE Trans. Ind. Appl. 2015, 48, 1064–1069. [Google Scholar] [CrossRef]
- Mandal, P.; Madhira, S.T.S.; Haque, A.U.; Meng, J.; Pineda, R.L. Forecasting Power Output of Solar Photovoltaic System Using Wavelet Transform and Artificial Intelligence Techniques. Procedia Comput. Sci. 2012, 12, 332–337. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Ward, J.K.; Tong, J.; Collins, L.; Platt, G. Machine learning for solar irradiance forecasting of photovoltaic system. Renew. Energy 2016, 90, 542–553. [Google Scholar] [CrossRef]
- Gers, F.A.; Schraudolph, N.N. Learning precise timing with LSTM recurrent networks. J. Mach. Learn. Res. 2003, 3, 115–143. [Google Scholar]
- Qureshi, A.S.; Khan, A.; Zameer, A.; Usman, A. Wind power prediction using deep neural network based meta regression and transfer learning. Appl. Soft Comput. 2017, 58, 742–755. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 2002, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Almeida, A.; Azkune, G. Predicting Human Behaviour with Recurrent Neural Networks. Appl. Sci. 2018, 8, 305. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Wang, F.; Yu, Y.; Zhang, Z.; Li, J.; Zhen, Z.; Li, K. Wavelet decomposition and convolutional LSTM networks based improved deep learning model for solar irradiance forecasting. Appl. Sci. 2018, 8, 1286. [Google Scholar]
- Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep Learning for solar power forecasting—An approach using AutoEncoder and LSTM Neural Networks. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 002858–002865. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Javed, K.; Gouriveau, R.; Zerhouni, N. SW-ELM: A summation wavelet extreme learning machine algorithm with a priori parameter initialization. Neurocomputing 2014, 123, 299–307. [Google Scholar] [CrossRef] [Green Version]
- Faraway, J.; Chatfield, C. Time series forecasting with neural networks: A comparative study using the airline data. Appl. Stat. 1998, 47, 231–250. [Google Scholar] [CrossRef]
- Cortez, B.; Carrera, B.; Kim, Y.J.; Jung, J.Y. An architecture for emergency event prediction using LSTM recurrent neural networks. Expert Syst. Appl. 2018, 97, 315–324. [Google Scholar] [CrossRef]
- Kingma, D.P.; Jimmy, L.B. Adma: A method for stochastic optimization. In ICLR; Arxiv.Org: Ithaca, NY, USA, 2015. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]













| Dates for All Seasons | Training Set | Validation Set | Test Set |
|---|---|---|---|
| Spring | 1 March 2017 to 10 May 2017 | 11 May to 13 May 2017 | 14 May to 16 May 2017 |
| Summer | 1 June to 31 July 2017 | 1 August to 3 August 2017 | 4 August to 6 August 2017 |
| Autumn | 1 September to 31 October 2017 | 1 November to 3 November 2017 | 4 November to 6 November 2017 |
| Winter | 1 December 2017 to 5 February 2018 | 6 February to 8 February 2018 | 9 February to 11 February 2018 |
| Layers and Parameters | |||
|---|---|---|---|
| Layers and Neurons of LSTM | Layers and Neurons of Dense | RMSE | MAPE |
| 1 (30) | 1 (80) | 11.26% | 2.72% |
| 2 (10, 10) | 2 (70, 80) | 8.21% | 2.01% |
| 3 (10, 10, 10) | 1 (80) | 11.18% | 2.76% |
| 4 (10, 10, 10, 30) | 2 (80, 80) | 12.30% | 2.95% |
| LSTM-Model | Learning Rate | Optimizer | Layers and Neurons of LSTM | Layers and Neurons of Dense | Dropout |
|---|---|---|---|---|---|
| #1 (Spring) | 0.01 | ADAM | 3 (10, 10, 10) | 1 (80) | 0.1 |
| #2 (Summer) | 0.01 | ADAM | 2 (10, 10) | 2 (70, 80) | \ |
| #3 (Autumn) | 0.15 | ADAM | 2 (10, 10) | 3 (70, 80, 80) | \ |
| #4 (Winter) | 0.01 | ADAM | 3 (10, 20, 20) | 1 (80) | \ |
| Season | BP | LSSVM | WNN | LSTM | |||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE (%) | MAPE (%) | RMSE (%) | MAPE (%) | RMSE (%) | MAPE (%) | RMSE (%) | MAPE (%) | ||
| Spring | training | 17.5% | 2.86% | 18.6% | 3.08% | 21.02% | 3.69% | 5.09% | 0.82% |
| forecasting | 19.6% | 4.82% | 20.1% | 5.37% | 18.8% | 4.8% | 5.34% | 1.51% | |
| Summer | training | 16.61% | 2.82% | 16.38% | 3.44% | 21.29% | 4.83% | 4.07% | 1.52% |
| forecasting | 13.03% | 3.18% | 13.3% | 2.85% | 19.05% | 4.68% | 9.57% | 2.01% | |
| Autumn | training | 21.91% | 3.14% | 21.71% | 3.28% | 26.99% | 4.38% | 4.96% | 1.06% |
| forecasting | 20.94% | 2.43% | 23.11% | 2.37% | 23.68% | 2.79% | 13.86% | 1.51% | |
| Winter | training | 24.05% | 2.45% | 24.68% | 2.42% | 29.85% | 3.16% | 3.38% | 0.38% |
| forecasting | 24.68% | 5.47% | 17.74% | 3.69% | 25.45% | 6% | 9.26% | 1.38% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Li, J.; Hong, F.; Long, D. Short-Term Forecasting of Power Production in a Large-Scale Photovoltaic Plant Based on LSTM. Appl. Sci. 2019, 9, 3192. https://doi.org/10.3390/app9153192
Gao M, Li J, Hong F, Long D. Short-Term Forecasting of Power Production in a Large-Scale Photovoltaic Plant Based on LSTM. Applied Sciences. 2019; 9(15):3192. https://doi.org/10.3390/app9153192
Chicago/Turabian StyleGao, Mingming, Jianjing Li, Feng Hong, and Dongteng Long. 2019. "Short-Term Forecasting of Power Production in a Large-Scale Photovoltaic Plant Based on LSTM" Applied Sciences 9, no. 15: 3192. https://doi.org/10.3390/app9153192
APA StyleGao, M., Li, J., Hong, F., & Long, D. (2019). Short-Term Forecasting of Power Production in a Large-Scale Photovoltaic Plant Based on LSTM. Applied Sciences, 9(15), 3192. https://doi.org/10.3390/app9153192