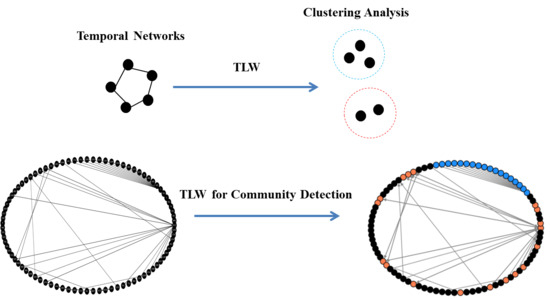
Temporal Label Walk for Community Detection and Tracking in Temporal Network
Abstract
:1. Introduction
- Propose a new method called Temporal Label Walk (TLW) to detect community structure in temporal networks without time window. Our approach transforms the community detection in network into a clustering analysis in vector space where no prior about the community structure is required. TLW can also maintain modularity at a reasonable level by combining time information.
- We reveal that simply mixing temporal data to snapshots and then measuring community structure is less effective with the course of time.
2. Our Method: Temporal Label Walk (TLW)
- Introduce the basic idea of our method including premise, feasibility, and process.
- Give mathematical definition of TLW.
- Measure the validation of community detection.
2.1. Basic Idea
2.2. Mathematical Definition
- Data sets are in the form of data streams,
- Interactions within communities are more frequent than those between communities.
- All temporal walks that end in v at , a new temporal walk starts from v and ends in u appears at . The variation of this new temporal walk is:where is an exponential decay function, is a constant and . We use to represent that interactions at are more important than those at .
- To maintain the timeliness of information, we define an enhancement function as another variation:where and is a unit vector with the vth element 1 and the rests 0. Note here v is the index of node v in set . Label value variation of u is:is the variation that u only interacts with v. Denoting by the set of all nodes that send messages to u at , variations of u is:At , the label value of u is also affected by . We can compute by:Set the label value . Then take the normalized vector of for the next iteration if to avoid the rapid growth of label value. To update label value of u at , the complete algorithm is described as follows:Computing label value can be regarded as a mapping , where is a snapshot at and . Community detection problem in temporal network can therefore be transformed to clustering analysis in high-dimensional vector space .
2.3. Evaluation
3. Experiment and Analysis
- Explain the importance of normalization,
- Use TLW to detect and track communities in real data sets and , and the modularity of several static methods including K-clique, label propagation, and asynchronous label propagation is given.
- Discuss the effects of parameters in experiments. We put this part in Section 4.
3.1. Normalization
3.2. Community Detection and Tracking
4. The Effects of Parameters
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Newman, M.E.J. Finding and Evaluating Community Structure in Networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Kernighan, B.W.; Lin, S. An Efficient Heuristic Procedure for Partitioning Graphs. Bell Syst. Tech. J. 1970, 49, 291–307. [Google Scholar] [CrossRef]
- Cordasco, G.; Gargano, L. Community detection via semi-synchronous label propagation algorithms. In Proceedings of the 2010 IEEE International Workshop on Business Applications of Social Network Analysis (BASNA), Bangalore, India, 15 December 2010; pp. 1–8. [Google Scholar]
- Rosval, M.; Bergstrom, C.T. Mapping change in large networks. PLoS ONE 2010, 5, e8694. [Google Scholar] [CrossRef] [PubMed]
- Studholme, C.; Hill, D.L.G.; Hawkes, D.J. An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognit. 1999, 32, 71–86. [Google Scholar] [CrossRef]
- Li, X.; Wu, B.; Guo, Q.; Zeng, X.; Shi, C. Dynamic community detection algorithm based on incremental identification. In Proceedings of the 2015 IEEE International Conference on Data Mining Workshop (ICDMW), Atlantic City, NJ, USA, 14–17 November 2015; pp. 900–907. [Google Scholar]
- Agarwal, P.; Verma, R.; Agarwal, A.; Chakraborty, T. DyPerm: Maximizing Permanence for Dynamic Community Detection. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Melbourne, VIC, Australia, 3–6 June 2018; pp. 437–449. [Google Scholar]
- Guo, Q.; Zhang, L.; Wu, B.; Zeng, X. Dynamic community detection based on distance dynamics. In Proceedings of the 2016 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM), San Francisco, CA, USA, 18–21 August 2016; pp. 329–336. [Google Scholar]
- DiTursi, D.J.; Ghosh, G.; Bogdanov, P. Local community detection in dynamic networks. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 847–852. [Google Scholar]
- Xie, J.; Chen, M.; Szymanski, B.K. LabelrankT: Incremental community detection in dynamic networks via label propagation. In Proceedings of the Proceedings of the Workshop on Dynamic Networks Management and Mining, New York, NY, USA, 22–27 June 2013; pp. 25–32. [Google Scholar]
- Sattari, M.; Zamanifar, K. A cascade information diffusion based label propagation algorithm for community detection in dynamic social networks. J. Comput. Sci. 2018, 25, 122–133. [Google Scholar] [CrossRef]
- Panzarasa, P.; Opsahl, T.; Carley, K.M. Patterns and dynamics of users’ behavior and interaction: Network analysis of an online community. J. Am. Soc. Inf. Sci. Technol. 2009, 60, 911–932. [Google Scholar] [CrossRef]
- Rozenshtein, P.; Gionis, A. Temporal pagerank. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Riva del Garda, Italy, 19–23 September 2016; pp. 674–689. [Google Scholar]
- Béres, F.; Pálovics, R.; Oláh, A.; Benczúr, A.A. Temporal walk based centrality metric for graph streams. Appl. Netw. Sci. 2018, 3, 32. [Google Scholar] [CrossRef] [PubMed]
- Pons, P.; Latapy, M. Computing communities in large networks using random walks. J. Graph Algorithms Appl. 2006, 10, 191–218. [Google Scholar] [CrossRef]
- Cai, B.; Wang, H.; Zeng, H.; Wang, H. Evaluation repeated random walks in community detection of social networks. In Proceedings of the 2010 International Conference on Machine Learning and Cybernetics, Qingdao, China, 11–14 July 2010; pp. 1849–1854. [Google Scholar]
- De Meo, P.; Ferrara, E.; Fiumara, G.; Provetti, A. Enhancing community detection using a network weighting strategy. Inf. Sci. 2013, 222, 648–668. [Google Scholar] [CrossRef] [Green Version]
- De Meo, P.; Ferrara, E.; Fiumara, G.; Provetti, A. Mixing local and global information for community detection in large networks. J. Comput. Syst. Sci. 2014, 80, 72–87. [Google Scholar] [CrossRef]
- Rémy, C.; Rym, B.; Matthieu, L. Tracking bitcoin users activity using community detection on a network of weak signals. In Proceedings of the International Conference on Complex Networks and Their Applications, Lyon, France, 29 November–1 December 2017; pp. 166–177. [Google Scholar]
- Frey, B.J.; Dueck, D. Clustering by passing messages between data points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef] [PubMed]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OQ, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Sculley, D. Web-scale k-means clustering. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; pp. 1177–1178. [Google Scholar]
- Viswanath, B.; Mislove, A.; Cha, M.; Gummadi, K.P. On the evolution of user interaction in facebook. In Proceedings of the 2nd ACM Workshop on Online Social Networks, Barcelona, Spain, 17 August 2009; pp. 37–42. [Google Scholar]
- Newman, M.E. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palla, G.; Derényi, I.; Farkas, I.; Vicsek, T. Uncovering the overlapping community structure of complex networks in nature and society. Nature 2005, 435, 814. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, U.N.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in large-scale networks. Phys. Rev. E 2007, 76, 036106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarmento, R.P.; Lemos, L.; Cordeiro, M.; Rossetti, G.; Cardoso, D. DynComm R Package–Dynamic Community Detection for Evolving Networks. arXiv 2019, arXiv:1905.01498. [Google Scholar]













| Method | Mini Batch K-Means | DBSCAN | AP |
|---|---|---|---|
| 1 day Modularity | 0.773 | 0.684 | 0.674 |
| 1 day Running time(s) | |||
| 1 week Running time(s) | |||
| 2 months Running time(s) |
| Method | K-Clique | Asynchronous | Label Propagation | DABP | TLW |
|---|---|---|---|---|---|
| 1 day | 0.780 | 0.780 | 0.780 | 0.587 | 0.773 |
| 1 week | 0.088 | 0.057 | 0.528 | 0.393 | 0.408 |
| 1 month | 0.051 | 0.045 | 0.205 | 0.276 | 0.311 |
| 2 months | 0.036 | 0.035 | 0.063 | 0.103 | 0.213 |
| 3 months | 0.038 | 0.032 | 0.088 | 0.069 | 0.225 |
| Method | K-Clique | Asynchronous | Label Propagation | TLW |
|---|---|---|---|---|
| 1 day (s) | ||||
| 1 week (s) | ||||
| 1 month (s) | ||||
| 2 months (s) | ||||
| 3 months(s) | ||||
| 4 months (s) |
| 0.643 | 0.642 | 0.660 | 0.650 | 0.685 | |
| 0.620 | 0.637 | 0.622 | 0.619 | 0.623 | |
| 0.569 | 0.560 | 0.553 | 0.544 | 0.508 | |
| 0.510 | 0.521 | 0.513 | 0.503 | 0.499 | |
| 0.406 | 0.478 | 0.365 | 0.301 | 0.216 | |
| 0.388 | 0.343 | 0.280 | 0.277 | 0.210 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wang, H.; Cheng, L.; Peng, W.; Li, X. Temporal Label Walk for Community Detection and Tracking in Temporal Network. Appl. Sci. 2019, 9, 3199. https://doi.org/10.3390/app9153199
Liu Z, Wang H, Cheng L, Peng W, Li X. Temporal Label Walk for Community Detection and Tracking in Temporal Network. Applied Sciences. 2019; 9(15):3199. https://doi.org/10.3390/app9153199
Chicago/Turabian StyleLiu, Zheliang, Hongxia Wang, Lizhi Cheng, Wei Peng, and Xiang Li. 2019. "Temporal Label Walk for Community Detection and Tracking in Temporal Network" Applied Sciences 9, no. 15: 3199. https://doi.org/10.3390/app9153199
APA StyleLiu, Z., Wang, H., Cheng, L., Peng, W., & Li, X. (2019). Temporal Label Walk for Community Detection and Tracking in Temporal Network. Applied Sciences, 9(15), 3199. https://doi.org/10.3390/app9153199