Development of Two Novel Hybrid Prediction Models Estimating Ultimate Bearing Capacity of the Shallow Circular Footing
Abstract
:1. Introduction
2. Methodology and Model Assessment
2.1. Artificial Neural Network
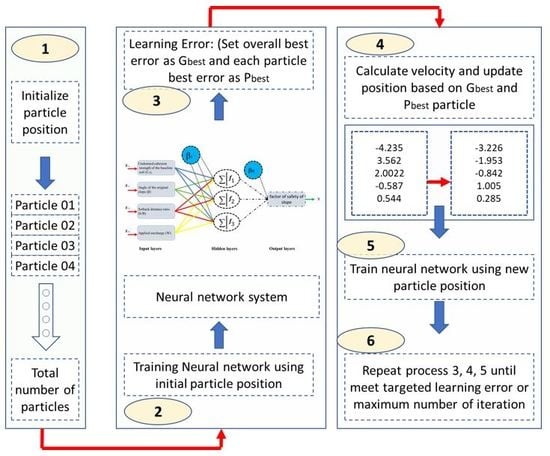
2.2. Particle Swarm Optimization (PSO)
2.3. Imperialist Competition Algorithm (ICA)
3. FEM Simulation and Data Collection
3.1. FEM Simulation
3.2. Model Assessment
4. Model Development for Fult Estimation
4.1. ANN Network Optimization
4.2. Hybrid PSO–ANN and ICA–ANN Models in Predicting Fult
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Asadi, A.; Moayedi, H.; Huat, B.B.; Parsaie, A.; Taha, M.R. Artificial neural networks approach for electrochemical resistivity of highly organic soil. Int. J. Electrochem. Sci 2011, 6, 1135–1145. [Google Scholar]
- Alrashed, A.A.A.A.; Karimipour, A.; Bagherzadeh, S.A.; Safaei, M.R.; Afrand, M. Electro- and thermophysical properties of water-based nanofluids containing copper ferrite nanoparticles coated with silica: Experimental data, modeling through enhanced ANN and curve fitting. Int. J. Heat Mass Transf. 2018, 127, 925–935. [Google Scholar] [CrossRef]
- Mojaddadi, H.; Pradhan, B.; Nampak, H.; Ahmad, N.; Ghazali, A.H.B. Ensemble machine-learning-based geospatial approach for flood risk assessment using multi-sensor remote-sensing data and GIS. Geomat. Nat. Hazards Risk 2017, 8, 1080–1102. [Google Scholar] [CrossRef] [Green Version]
- Azeez, O.S.; Pradhan, B.; Shafri, H.Z.; Shukla, N.; Lee, C.-W.; Rizeei, H.M. Modeling of CO emissions from traffic vehicles using artificial neural networks. Appl. Sci. 2019, 9, 313. [Google Scholar] [CrossRef]
- Bowles, J.E. Foundation Analysis and Design; McGraw-hill: New York, NY, USA, 1996. [Google Scholar]
- Nazir, R.; Moayedi, H. Soil Mass Loss Reduction during Rainfalls by Reinforcing the Slopes with the Surficial Confinement. World Acad. of Sci., Eng. Technol., Int. J. of Environ., Ecol., Geomat., Earth Sci. Eng. 2014, 8, 331–334. [Google Scholar]
- Nazir, R.; Ghareh, S.; Mosallanezhad, M.; Moayedi, H. The influence of rainfall intensity on soil loss mass from cellular confined slopes. Measurement 2016, 81, 13–25. [Google Scholar] [CrossRef]
- Bui, D.T.; Moayedi, H.; Gör, M.; Jaafari, A.; Foong, L.K. Predicting slope stability failure through machine learning paradigms. Isprs Int. Geo-Inf. 2019, 8, 395. [Google Scholar] [CrossRef]
- Moayedi, H.; Bui, D.T.; Gör, M.; Pradhan, B.; Jaafari, A. The feasibility of three prediction techniques of the artificial neural network, adaptive neuro-fuzzy inference system, and hybrid particle swarm optimization for assessing the safety factor of cohesive slopes. Isprs Int. Geo-Inf. 2019, 8, 391. [Google Scholar] [CrossRef]
- Meyerhof, G.G.; Hanna, A.M. Ultimate bearing capacity of foundations on layered soils under inclined load. Can. Geotech J. 1978, 15, 565–572. [Google Scholar] [CrossRef]
- Niroumand, H.; Kassim, K.A.; Nazir, R.; Faizi, K.; Adhami, B.; Moayedi, H.; Loon, W. Slope stability and sheet pile and contiguous bored pile walls. Electron. J. Geotech. Eng. 2012, 17, 19–27. [Google Scholar]
- Chakraborty, A.; Goswami, D. Prediction of slope stability using multiple linear regression (MLR) and artificial neural network (ANN). Arab. J. Geosci. 2017, 10, 11. [Google Scholar] [CrossRef]
- Nguyen, H.; Moayedi, H.; Foong, L.K.; Al Najjar, H.A.H.; Jusoh, W.A.W.; Rashid, A.S.A.; Jamali, J. Optimizing ANN models with PSO for predicting short building seismic response. Eng. Comput. 2019, 35, 1–15. [Google Scholar] [CrossRef]
- Moayedi, H.; Moatamediyan, A.; Nguyen, H.; Bui, X.-N.; Bui, D.T.; Rashid, A.S.A. Prediction of ultimate bearing capacity through various novel evolutionary and neural network models. Eng. Comput. 2019, 35, 1–17. [Google Scholar] [CrossRef]
- Rashid, A.S.A.; Kalatehjari, R.; Noor, N.M.; Yaacob, H.; Moayedi, H.; Sing, L.K. Relationship between liquidity index and stabilized strength of local subgrade materials in a tropical area. Measurement 2014, 55, 231–237. [Google Scholar] [CrossRef]
- Moayedi, H.; Mosallanezhad, M.; Nazir, R. Evaluation of Maintained Load Test (MLT) and Pile Driving Analyzer (PDA) in Measuring Bearing Capacity of Driven Reinforced Concrete Piles. Soil Mech. Found. Eng. 2017, 54, 150–154. [Google Scholar] [CrossRef]
- Moayedi, H.; Nazir, R.; Ghareh, S.; Sobhanmanesh, A.; Tan, Y.C. Performance Analysis of a Piled Raft Foundation System of Varying Pile Lengths in Controlling Angular Distortion. Soil Mech. Found. Eng. 2018, 55, 265–269. [Google Scholar] [CrossRef]
- Momeni, E.; Armaghani, D.J.; Fatemi, S.A.; Nazir, R. Prediction of bearing capacity of thin-walled foundation: A simulation approach. Eng. Comput. 2018, 34, 319–327. [Google Scholar] [CrossRef]
- Ranjan, G.; Rao, A.S.R. Basic and Applied Soil Mechanics; New Age International: Kerala, India, 2007. [Google Scholar]
- Das, B.M. Principles of Foundation Engineering, 8th ed.; McGraw-Hill Book Co.: Singapore, 2008. [Google Scholar]
- Moayedi, H.; Hayati, S. Modelling and optimization of ultimate bearing capacity of strip footing near a slope by soft computing methods. Appl. Soft Comput. 2018, 66, 208–219. [Google Scholar] [CrossRef]
- Haghbin, M. Bearing Capacity of Strip Footings Resting on Granular Soil Overlying Soft Clay. Int. J. Civ. Eng. 2016, 14, 467–477. [Google Scholar] [CrossRef]
- Lotfizadeh, M.R.; Kamalian, M. Estimating Bearing Capacity of Strip Footings over Two-Layered Sandy Soils Using the Characteristic Lines Method. Int. J. Civ. Eng. 2016, 14, 107–116. [Google Scholar] [CrossRef]
- Ahmadi, M.M.; Kouchaki, B.M. New and Simple Equations for Ultimate Bearing Capacity of Strip Footings on Two-Layered Clays: Numerical study. Int. J. Geomech. 2016, 16, 11. [Google Scholar] [CrossRef]
- McCulloch, W.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Hebb, D. The Organization of Behavior: A Neurophysiological Approach; Wiley: Hoboken, NJ, USA, 1949. [Google Scholar]
- Binh Thai, P.; Prakash, I.; Dieu Tien, B. Spatial prediction of landslides using a hybrid machine learning approach based on Random Subspace and Classification and Regression Trees. Geomorphology 2018, 303, 256–270. [Google Scholar]
- Dieu Tien, B.; Viet-Ha, N.; Nhat-Duc, H. Prediction of soil compression coefficient for urban housing project using novel integration machine learning approach of swarm intelligence and Multi-layer Perceptron Neural Network. Adv. Eng. Inform. 2018, 38, 593–604. [Google Scholar] [CrossRef]
- Sharma, L.K.; Singh, R.; Umrao, R.K.; Sharma, K.M.; Singh, T.N. Evaluating the modulus of elasticity of soil using soft computing system. Eng. Comput. 2017, 33, 497–507. [Google Scholar] [CrossRef]
- Shahri, A.A. An Optimized Artificial Neural Network Structure to Predict Clay Sensitivity in a High Landslide Prone Area Using Piezocone Penetration Test (CPTu) Data: A Case Study in Southwest of Sweden. Geotech. Geol. Eng. 2016, 34, 745–758. [Google Scholar] [CrossRef]
- Saghatforoush, A.; Monjezi, M.; Faradonbeh, R.S.; Armaghani, D.J. Combination of neural network and ant colony optimization algorithms for prediction and optimization of flyrock and back-break induced by blasting. Eng. Comput. 2016, 32, 255–266. [Google Scholar] [CrossRef]
- Gao, W.; Wu, H.; Siddiqui, M.K.; Baig, A.Q. Study of biological networks using graph theory. Saudi J. Biol. Sci. 2018, 25, 1212–1219. [Google Scholar] [CrossRef]
- Gao, W.; Guirao, J.L.G.; Basavanagoud, B.; Wu, J. Partial multi-dividing ontology learning algorithm. Inf. Sci. 2018, 467, 35–58. [Google Scholar] [CrossRef]
- Gao, W.; Wang, W.; Dimitrov, D.; Wang, Y. Nano properties analysis via fourth multiplicative ABC indicator calculating. Arab. J. Chem. 2018, 11, 793–801. [Google Scholar] [CrossRef]
- Gao, W.; Guirao, J.L.G.; Abdel-Aty, M.; Xi, W. An independent set degree condition for fractional critical deleted graphs. Discret. Contin. Dyn. Syst. -S 2019, 12, 877–886. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.; Bui, X.-N.; Bui, H.-B.; Mai, N.-L. A comparative study of artificial neural networks in predicting blast-induced air-blast overpressure at Deo Nai open-pit coal mine, Vietnam. Neural Comput. Appl. 2018, 1–17. [Google Scholar] [CrossRef]
- Bui, X.-N.; Nguyen, H.; Le, H.-A.; Bui, H.-B.; Do, N.-H. Prediction of Blast-induced Air Over-pressure in Open-Pit Mine: Assessment of Different Artificial Intelligence Techniques. Nat. Resour. Res. 2019, 1–21. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.-N.; Tran, Q.-H.; Mai, N.-L. A new soft computing model for estimating and controlling blast-produced ground vibration based on hierarchical K-means clustering and cubist algorithms. Appl. Soft Comput. 2019, 77, 376–386. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Micro Machine and Human Science, Proceedings of the Sixth International Symposium on Micro Machine and Human Science, 1995; IEEE: Nagoya, Japan, 1995; pp. 39–43. [Google Scholar]
- Huang, C.-L.; Dun, J.-F. A distributed PSO–SVM hybrid system with feature selection and parameter optimization. Appl. Soft Comput. 2008, 8, 1381–1391. [Google Scholar] [CrossRef]
- Wan, S.; Yen, J.Y.; Lin, C.Y.; Chou, T.Y. Construction of knowledge-based spatial decision support system for landslide mapping using fuzzy clustering and KPSO analysis. Arab. J. Geosci. 2015, 8, 1041–1055. [Google Scholar] [CrossRef]
- Zhang, X.; Nguyen, H.; Bui, X.; Tran, Q.; Nguyen, D.; Bui, D.; Moayedi, H. Novel Soft Computing Model for Predicting Blast-Induced Ground Vibration in Open-Pit Mines Based on Particle Swarm Optimization and XGBoost. Nat. Resour. Res. 2019, 28, 1–11. [Google Scholar] [CrossRef]
- Yuan, C.; Moayedi, H. Evaluation and comparison of the advanced metaheuristic and conventional machine learning methods for prediction of landslide occurrence. Eng. Comput. 2019, 36, 1–11. [Google Scholar] [CrossRef]
- Yuan, C.; Moayedi, H. The performance of six neural-evolutionary classification techniques combined with multi-layer perception in two-layered cohesive slope stability analysis and failure recognition. Eng. Comput. 2019, 36, 1–10. [Google Scholar] [CrossRef]
- Xi, W.; Li, G.; Moayedi, H.; Nguyen., H. A particle-based optimization of artificial neural network for earthquake-induced landslide assessment in Ludian county, China. Geomat. Nat. Hazards Risk 2019, 10, 1750–1771. [Google Scholar] [CrossRef] [Green Version]
- Moayedi, H.; Mosallanezhad, M.; Mehrabi, M.; Safuan, A.R.A.; Biswajeet, P. Modification of landslide susceptibility mapping using optimized PSO-ANN technique. Eng. Comput. 2018, 35, 967–984. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the CEC 2007. IEEE Congress on Evolutionary Computation, 2007; IEEE: Singapore; pp. 4661–4667.
- Mosallanezhad, M.; Moayedi, H. Developing hybrid artificial neural network model for predicting uplift resistance of screw piles. Arab. J. Geosci. 2017, 10, 479. [Google Scholar] [CrossRef]
- Moayedi, H.; Armaghani, D.J. Optimizing an ANN model with ICA for estimating bearing capacity of driven pile in cohesionless soil. Eng. Comput. 2017, 34, 347–356. [Google Scholar] [CrossRef]
- Mosallanezhad, M.; Moayedi, H. Comparison Analysis of Bearing Capacity Approaches for the Strip Footing on Layered Soils. Arab. J. Sci. Eng. 2017, 42, 3711–3722. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, M.X.; Dai, Z.H.; Li, J.Z.; Zeng, F.F. Bearing capacity of strip foundations in horizontal-vertical reinforced soils. Geotext. Geomembr. 2017, 45, 29–34. [Google Scholar] [CrossRef]
- Anvari, S.M.; Shooshpasha, I. Influence of size of granulated rubber on bearing capacity of fine-grained sand. Arab. J. Geosci. 2016, 9, 707. [Google Scholar] [CrossRef]
- Noorzad, R.; Manavirad, E. Bearing capacity of two close strip footings on soft clay reinforced with geotextile. Arab. J. Geosci. 2014, 7, 623–639. [Google Scholar] [CrossRef]
- Gao, W.; Dimitrov, D.; Abdo, H. Tight independent set neighborhood union condition for fractional critical deleted graphs and ID deleted graphs. Discret. Contin. Dyn. Syst. -S 2018, 12, 711–721. [Google Scholar] [CrossRef]




















| Ground Conditions | Foundation Diameter (B) (m) | (Upper Layer Thickness/Foundation Width) or h/B |
|---|---|---|
| Soil layer S1 on soil layer (S2, S3, S4, S5, S6, S7, S8) | 1.0 | 0, 0.2, 0.4, 0.8, 1.0, |
| Soil layer S8 on soil layer (S1, S2, S3, S4, S5, S6, S7) |
| Model | Inputs | Output | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Top Layer Properties | Bottom Layer Properties | ||||||||||||
| h/B | Settlement | Fult | |||||||||||
| (deg) | (deg) | kN/m3 | kPa | - | (deg) | (deg) | kN/m3 | kPa | - | - | mm | kPa | |
| 1 | 30 | 3.4 | 19 | 17500 | 0.333 | 33 | 5.8 | 19.9 | 25000 | 0.313 | 0.2 | 30.362 | 297.789 |
| 2 | 30 | 3.4 | 19 | 17500 | 0.333 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 0.2 | 30.358 | 641.312 |
| 3 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 36 | 8 | 20.5 | 35000 | 0.291 | 0.6 | 30.324 | 819.291 |
| 4 | 30 | 3.4 | 19 | 17500 | 0.333 | 34 | 6.4 | 20.1 | 27500 | 0.306 | 1 | 30.279 | 229.515 |
| 5 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 36 | 8 | 20.5 | 35000 | 0.291 | 0.2 | 30.264 | 645.802 |
| 6 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 31 | 4.2 | 19.3 | 20000 | 0.327 | 0.2 | 30.257 | 351.505 |
| 7 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 34 | 6.4 | 20.1 | 27500 | 0.306 | 0.6 | 30.175 | 674.178 |
| 8 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 39 | 10 | 20.9 | 50000 | 0.27 | 0.2 | 30.112 | 932.268 |
| 9 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 39 | 10 | 20.9 | 50000 | 0.27 | 0.8 | 30.071 | 1096.348 |
| 10 | 30 | 3.4 | 19 | 17500 | 0.333 | 37 | 8.8 | 20.7 | 40000 | 0.285 | 0.2 | 30.050 | 439.321 |
| 11 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 36 | 8 | 20.5 | 35000 | 0.291 | 0.4 | 30.041 | 739.102 |
| 12 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 37 | 8.8 | 20.7 | 40000 | 0.285 | 0.2 | 30.040 | 735.445 |
| 13 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 30 | 3.4 | 19 | 17500 | 0.333 | 0.2 | 30.005 | 307.149 |
| 14 | 30 | 3.4 | 19 | 17500 | 0.333 | 36 | 8 | 20.5 | 35000 | 0.291 | 0.4 | 29.973 | 292.666 |
| 15 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 34 | 6.4 | 20.1 | 27500 | 0.306 | 1 | 29.972 | 823.612 |
| 16 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 33 | 5.8 | 19.9 | 25000 | 0.313 | 0.8 | 29.949 | 692.368 |
| 17 | 30 | 3.4 | 19 | 17500 | 0.333 | 34 | 6.4 | 20.1 | 27500 | 0.306 | 0.2 | 29.942 | 324.735 |
| 18 | 30 | 3.4 | 19 | 17500 | 0.333 | 36 | 8 | 20.5 | 35000 | 0.291 | 0.6 | 29.940 | 249.580 |
| 19 | 30 | 3.4 | 19 | 17500 | 0.333 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 0.6 | 29.934 | 251.650 |
| 20 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 39 | 10 | 20.9 | 50000 | 0.27 | 0.6 | 29.904 | 1054.378 |
| 21 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 37 | 8.8 | 20.7 | 40000 | 0.285 | 0.6 | 29.884 | 896.035 |
| 22 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 39 | 10 | 20.9 | 50000 | 0.27 | 1 | 29.856 | 1124.575 |
| 23 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 34 | 6.4 | 20.1 | 27500 | 0.306 | 0.8 | 29.831 | 742.268 |
| 24 | 30 | 3.4 | 19 | 17500 | 0.333 | 31 | 4.2 | 19.3 | 20000 | 0.327 | 1 | 29.829 | 220.100 |
| 25 | 30 | 3.4 | 19 | 17500 | 0.333 | 31 | 4.2 | 19.3 | 20000 | 0.327 | 0.6 | 29.817 | 225.296 |
| 26 | 30 | 3.4 | 19 | 17500 | 0.333 | 31 | 4.2 | 19.3 | 20000 | 0.327 | 0.8 | 29.801 | 221.703 |
| 27 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 33 | 5.8 | 19.9 | 25000 | 0.313 | 0.4 | 29.784 | 533.911 |
| 28 | 42 | 11.5 | 21.1 | 65000 | 0.249 | 34 | 6.4 | 20.1 | 27500 | 0.306 | 0.2 | 29.771 | 497.129 |
| 29 | 30 | 3.4 | 19 | 17500 | 0.333 | 37 | 8.8 | 20.7 | 40000 | 0.285 | 0.8 | 29.709 | 239.304 |
| 30 | 30 | 3.4 | 19 | 17500 | 0.333 | 31 | 4.2 | 19.3 | 20000 | 0.327 | 0.4 | 29.701 | 230.895 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moayedi, H.; Kalantar, B.; Dounis, A.; Tien Bui, D.; Foong, L.K. Development of Two Novel Hybrid Prediction Models Estimating Ultimate Bearing Capacity of the Shallow Circular Footing. Appl. Sci. 2019, 9, 4594. https://doi.org/10.3390/app9214594
Moayedi H, Kalantar B, Dounis A, Tien Bui D, Foong LK. Development of Two Novel Hybrid Prediction Models Estimating Ultimate Bearing Capacity of the Shallow Circular Footing. Applied Sciences. 2019; 9(21):4594. https://doi.org/10.3390/app9214594
Chicago/Turabian StyleMoayedi, Hossein, Bahareh Kalantar, Anastasios Dounis, Dieu Tien Bui, and Loke Kok Foong. 2019. "Development of Two Novel Hybrid Prediction Models Estimating Ultimate Bearing Capacity of the Shallow Circular Footing" Applied Sciences 9, no. 21: 4594. https://doi.org/10.3390/app9214594
APA StyleMoayedi, H., Kalantar, B., Dounis, A., Tien Bui, D., & Foong, L. K. (2019). Development of Two Novel Hybrid Prediction Models Estimating Ultimate Bearing Capacity of the Shallow Circular Footing. Applied Sciences, 9(21), 4594. https://doi.org/10.3390/app9214594