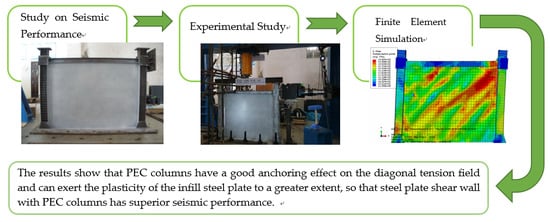
Study on Seismic Performance and Damage Analysis of Steel Plate Shear Wall with Partially Encased Composite (PEC) Columns
Abstract
:1. Introduction
2. Experimental Study
2.1. Specimen Design
2.2. Test Setup
2.3. Loading Program
2.4. Measuring-Point Arrangement
2.5. Damage Processes
2.6. Experimental Result Analyses
2.6.1. Loading-Displacement Curve
2.6.2. Skeleton Curve
2.6.3. Stress Distribution and Damage Analysis
- (1)
- Stress analysis of PEC columnsWhen the displacement reached 26 mm in 20th cycle, the infill steel plate had been yielded, but the stress of PEC columns was still small and the safety stock was still high. When loading forward to the right in the positive direction, the left flange of the PEC column near the side of lateral actuator (Z1, Z4, Z5, Z8, Z9, Z12, Z17, Z20, Z21, Z24, Z25, Z28) was in tension and the right flange away from side of lateral actuator (Z2, Z3, Z6, Z7, Z10, Z11, Z18, Z19, Z22, Z23, Z26, Z27) were in compression. When loading forward to the left in the negative direction, on the contrary, the right flange was in tension and the left flange was in compression. Since it was directly connected with the actuator, the deformation and the stress of left column were obviously greater than that of the right column. The right column had small deformations and stresses because of the buffer function provided by the deformation of the steel plate. According to the test data, the maximum stress of PEC columns and the concrete were 186 MPa and 27 MPa respectively when the steel plate was basically yielding. Therefore, when the steel plate was yielded, PEC columns still had high emergency capacity to ensure the stability of the framework and the occurrence of the yielding dissipation of the steel plate prior to the occurrence of the damage of the whole structure. The concrete stress was uniformly distributed in the normal working state, and the maximum value of concrete was 27.63 MPa. Therefore, the concrete was not damaged, and the stress can be continuously increased.
- (2)
- Stress analysis of infill steel plateBased on the analysis of the data, the upper end of the steel plate was pushed by the actuator from left to right when the displacement reaches +26 mm. At this moment, the main diagonal line H17-H24 suffered from the maximum stress that was more than 500 MPa. Meanwhile, we found that the stress of H4 was also large (reaching up to 400 MPa), indicating that the width of diagonal tension strip extended in the direction of the other diagonal line. Besides the stress in the main diagonal region (H18-H23-T5) reaches yield, the counter-diagonal (T11-T15 and T12-T16) also began to yield and dissipate energy. The yield area of the whole steel plate shear wall was about 2/3. Additionally, the stress of the upper part was usually greater than that of the lower part for the strain gages outside of the main diagonal line. Generally speaking, the steel plate has been significantly yielded at the value of +26 mm. When the displacement reached −29 mm in 21st cycle, there were results corresponding to the above analysis. In addition, it should be noted that the local stress in the corner is generally larger, while the stress in the middle, such as T16, was smaller.
2.6.4. Deformation Analysis
3. The Comparison of Finite Element and Experimental Results
3.1. Finite Element Modeling
3.1.1. Material Behaviors Modeling
3.1.2. Models of Steel Plate Shear Walls with PEC Columns
3.1.3. Loading Program
3.2. Comparison and Analysis
3.2.1. Failure Mode
3.2.2. Skeleton Curve
3.3. Summary
4. Parametric Analysis
4.1. Height-Thickness Ratio λ
4.2. Strength Grade of Concrete
4.3. Axial Compression Ratio μ
5. Conclusions and Future Work
- (1)
- It is found that the steel plate shear wall with PEC columns has better mechanical properties and superior seismic performance by finite element analysis and test research. The results show that the introduction of PEC columns into steel plate shear walls plays an outstanding role in improving the seismic performance of steel plate shear wall and exerting the advantages of deformation and energy dissipation of the infill steel plates.
- (2)
- The hysteretic behaviors of steel plate shear wall with PEC columns are stable, and the hysteretic curves are relatively full. The energy dissipation capacity is stable. The energy dissipation coefficient reaches 3.82 and 2.27 by using the finite element analysis and test, respectively. The energy dissipation coefficient is larger obtained by the finite element analysis and experiment.
- (3)
- PEC columns have a good anchoring effect on diagonal tension field of steel plate shear wall. The steel plate yield before the failure of PEC columns. The damage of the steel plate presents a remarkable “stripe” feature, and the concave-convex buckling is formed along the diagonal line where the stress is maximum.
- (4)
- The height-thickness ratio λ as the main parameter of the steel plate has a large effect on the ultimate strength and the hysteretic performance of steel plate shear wall with PEC columns. With the increase of height-thickness ratio, the hysteretic loop becomes full, the increase of ultimate bearing capacity is between 10% and 30%. The concrete strength as the main influential parameter on the axial compressive strength of PEC columns has little effect on the lateral resistance of the steel plate shear wall with PEC columns, and hysteretic behavior with the different grade concrete has little change. The axial compression ratio μ has a great effect on the ultimate bearing capacity of the structure. The ultimate strength and energy dissipation capacity decrease with the increasing of axial compression ratio μ.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Takahash, T.; Takemoto, Y. Experimental Study on Thin Steel Shear Walls and Particular Bracings under Altermative Horizontal Load. In IABSE Symposium on Resistance and Ultimate Deformability of Structures Acted on by Well-Defined Repeated Loads; International Association for Bridges and Structural Engineering: Lisbon, Portugal, 1973; pp. 185–191. [Google Scholar]
- Sabouri-Ghomi, S.; Roberts, T.M. Nonlinear dynamic analysis of steel plate shear walls including shear and bending deformations. Eng. Struct. 1992, 14, 309–317. [Google Scholar] [CrossRef]
- Roberts, T.M.; Sabouri-Ghomi, S. Hysteretic characteristics of unstiffened plate shear panels. Thin-Walled Struct. 1991, 12, 145–162. [Google Scholar] [CrossRef]
- Roberts, T.M.; Sabouri-Ghomi, S. Hysteretic characteristics of unstiffened perforated steel plate shear panels. Thin-Walled Struct. 1992, 14, 139–151. [Google Scholar] [CrossRef]
- Verma, A.; Sahoo, D.R. Seismic Collapse Analysis of Steel Plate Shear Wall Systems. Key Eng. Mater. 2018, 763, 702–708. [Google Scholar] [CrossRef]
- Verma, A.; Sahoo, D.R. Seismic performance of staggered steel plate shear wall systems in high rise buildings. Earthq. Eng. Struct. Dyn. 2017, 1, 3181–3189. [Google Scholar] [CrossRef]
- Lu, X.Z.; Xie, L.; Guan, H.; Huang, Y.L.; Lu, X. A shear wall element for nonlinear seismic analysis of super-tall buildings using OpenSees. Finite Elem. Anal. Des. 2015, 98, 14–25. [Google Scholar] [CrossRef] [Green Version]
- Mashhadiali, N.; Gholhaki, M.; Zahiri-Hshhem, R. Technical Note: Analytical Evaluation of the Vulnerability of Framed Tall Buildings with Steel Plate Shear Wall to Progressive Collapse. Int. J. Civ. Eng. 2016, 14, 595–608. [Google Scholar] [CrossRef]
- Wang, M.; Yang, W.G.; Shi, Y.J.; Xu, J. Seismic behaviors of steel plate shear wall structures with construction details and materials. J. Constr. Steel Res. 2015, 107, 194–210. [Google Scholar] [CrossRef]
- Zirakian, T.; Zhang, J. Seismic design and behavior of low yield point steel plate shear walls. Int. J. Steel Struct. 2015, 15, 135–151. [Google Scholar] [CrossRef]
- Berman, J.W. Seismic behavior of code designed steel plate shear walls. Steel Constr. 2011, 33, 230–244. [Google Scholar] [CrossRef]
- Bhowmick, A.K. Seismic behavior of steel plate shear walls with centrally placed circular perforations. Steel Constr. 2014, 75, 30–42. [Google Scholar] [CrossRef]
- Xu, W.F.; Yang, X.; Wang, F.L. Experimental investigation on the seismic behavior of newly-developed precast reinforced concrete block masonry shear walls. Appl. Sci. 2018, 8, 1071. [Google Scholar] [CrossRef]
- Jiang, S.F.; Lian, S.H.; Zhao, J.; Li, X.; Ma, S.L. Influence of a new form of bolted connection on the mechanical behaviors of a PC shear wall. Appl. Sci. 2018, 8, 1381. [Google Scholar] [CrossRef]
- Xue, M.; Lu, L.W. Interaction of infilled steel plate shear wall panels with surrounding frame members. In Proceeding of the Structureal Stability Research Council Annual Technical Session, Bethlehem, PA, USA, 11–12 April 1994; pp. 339–354. [Google Scholar]
- Lubell, A.S.; Prion, H.G.L.; Ventura, C.E.; Rezai, M. Unstiffened Steel Plate Shear Wall Performance under Cyclic Loading. J. Struct. Eng. 2000, 127, 453–460. [Google Scholar] [CrossRef]
- Astaneh-Asl, A.; Liu, J.; Mcmullin, K.M. Behavior and design of single plate shear connections. J. Constr. Steel Res. 2002, 58, 1121–1141. [Google Scholar] [CrossRef]
- Hitaka, T.; Matsui, C. Experimental Study on Steel Shear Wall with Slits. J. Struct. Eng. 2003, 129, 586–595. [Google Scholar] [CrossRef]
- Sabourighomi, S.; Mamazizi, S. Experimental investigation on stiffened steel plate shear walls with two rectangular openings. Thin-Walled Struct. 2015, 86, 56–66. [Google Scholar] [CrossRef]
- Jin, S.S.; Bai, J.L.; Ou, J. Seismic behavior of a buckling-restrained steel plate shear wall with inclined slots. J. Constr. Steel Res. 2017, 129, 1–11. [Google Scholar] [CrossRef]
- Wang, P.J.; Xue, Z.P.; Xiao, S.W. Seismic behavior of Self-Buckling-Restrained Steel Plate Shear Wall made by two incline-slotted infill plates. J. Constr. Steel Res. 2017, 133, 47–64. [Google Scholar] [CrossRef]
- Lu, J.Y.; Yu, S.J.; Xia, J.; Qiao, X.D.; Tang, Y. Experimental study on the hysteretic behavior of steel plate shear wall with unequal length slits. J. Constr. Steel Res. 2018, 147, 477–487. [Google Scholar] [CrossRef]
- Li, J.B.; Wang, Y.; Lu, Z.; Li, J.Z. Experimental Study and Numerical Simulation of a Laminated Reinforced Concrete Shear Wall with a Vertical Seam. Appl. Sci. 2017, 7, 629. [Google Scholar] [Green Version]
- Zirakian, T.; Zhang, J. Structural performance of unstiffened low yield point steel plate shear walls. J. Constr. Steel Res. 2015, 112, 40–53. [Google Scholar] [CrossRef]
- Nie, J.G.; Zhu, L. Lateral stiffness of steel plate shear walls. Sci. China 2014, 57, 151–162. [Google Scholar] [CrossRef]
- Clayton, P.M.; Berman, J.W.; Lowes, L.N. Subassembly testing and modeling of self-centering steel plate shear walls. Eng. Struct. 2013, 56, 1848–1857. [Google Scholar] [CrossRef]
- Clayton, P.M.; Berman, J.W.; Lowes, L.N. Seismic performance of self-centering steel plate shear walls with beam-only-connected web plates. J. Constr. Steel Res. 2015, 106, 198–208. [Google Scholar] [CrossRef] [Green Version]
- Clayton, P.M.; Dowden, D.M.; Chaohsien, L.I.; Berman, J.W.; Bruneau, M.; Lowes, N.L.; Tsai, K. Self-centering steel plate shear walls for improving seismic resilience. Front. Struct. Civ. Eng. 2016, 10, 283–290. [Google Scholar] [CrossRef]
- Clayton, P.M.; Tsai, C.; Berman, J.W.; Lowes, L.N. Comparison of web plate numerical models for self-centering steel plate shear walls. Earthq. Eng. Struct. Dyn. 2015, 44, 2093–2110. [Google Scholar] [CrossRef]
- Verma, A.; Sahoo, D.R. Estimation of lateral force contribution of boundary elements in steel plate shear wall systems. Earthq. Engng Struct. Dyn. 2017, 46, 1081–1098. [Google Scholar] [CrossRef]
- Ricles, J.M.; Paboojian, S.D. Seismic performance of steel-encased composite columns. J. Struct. Eng. 1994, 120, 2474–2494. [Google Scholar] [CrossRef]
- Shanmugam, N.E.; Lakshmi, B. State of the art report on steel–concrete composite columns. J. Constr. Steel Res. 2001, 57, 1041–1080. [Google Scholar] [CrossRef]
- Tremblay, R.; Massicotte, B. Experimental Study on the Behavior of Partially Encased Composite Columns Made with Light Welded H Steel Shapes under Compressive Axial Loads; Structral Stability Research Council 1998 Annual Technical Session & Meeting; Trans Tech Publications: Atlanta, GA, USA, 1998; pp. 195–204. [Google Scholar]
- Chicoine, T.; Tremblay, R.; Massicotte, B.; James, M.R.; Lu, L. Behavior and Strength of Partially Encased Composite Columns with Built-up Shapes. J. Struct. Eng. 2002, 128, 279–288. [Google Scholar] [CrossRef]
- Begum, M.; Drivers, R.G.; Elwi, A.E. Finite element modeling of partially encased composite columns using the dynamic explicit solution method. J. Struct. Eng. 2007, 133, 326–334. [Google Scholar] [CrossRef]
- Rahman, M.S.; Begum, M. Numerical simulations of fully encased composite columns under gravity loads. Appl. Mech. Mater. 2016, 860, 140–145. [Google Scholar] [CrossRef]
- Karimi, K.; Tait, M.J.; El-Dakhakhni, W.W. Testing and modeling of a novel FRP-encased steel–concrete composite column. Comp. Struct. 2011, 93, 1463–1473. [Google Scholar] [CrossRef]
- Zhao, G.T.; Feng, C. Axial Ultimate Capacity of Partially Encased Composite Columns. Appl. Mech. Mater. 2012, 166–169, 292–295. [Google Scholar] [CrossRef]
- Begum, M.; Driver, R.G.; Elwi, A.E. Behaviour of partially encased composite columns with high strength concrete. Eng. Struct. 2013, 56, 1718–1727. [Google Scholar] [CrossRef]
- Zhao, G.T.; Hu, Q.W. Seismic Behavior of Partially Encased Concrete Composite Columns. Appl. Mech. Mater. 2015, 777, 190–193. [Google Scholar] [CrossRef]
- Song, Y.C.; Wang, R.P.; Li, J. Local and post-local buckling behavior of welded steel shapes in partially encased composite columns. Thin-Walled Struct. 2016, 108, 93–108. [Google Scholar] [CrossRef]
- Marinopoulou, A.A.; Balopoulos, V.D.; Kalfas, C.N. Simulation of partially encased composite steel–concrete columns with steel columns. J. Constr. Steel Res. 2007, 63, 1058–1065. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Wang, T.; Yang, J.; Zhao, X.Z. Test and numerical simulation of partially encased composite columns subject to axial and cyclic horizontal loads. Int. J. Steel Struct. 2010, 10, 385–393. [Google Scholar] [CrossRef]
- Ellobody, E.; Young, B. Numerical simulation of concrete encased steel composite columns. J. Const. Steel Res. 2011, 67, 211–222. [Google Scholar] [CrossRef]
- Piquer, A.; Hernández-Figueirido, D. Protected steel columns vs partially encased columns: Fire resistance and economic considerations. J. Constr. Steel Res. 2016, 124, 47–56. [Google Scholar] [CrossRef] [Green Version]
- Ahn, J.K.; Lee, C.H. Fire behavior and resistance of partially encased and slim-floor composite beams. J. Constr. Steel Res. 2017, 129, 276–285. [Google Scholar] [CrossRef]
- Peng, J.X.; Hu, S.W.; Zhang, J.R.; Cai, C.S.; Li, L.Y. Influence of cracks on chloride diffusivity in concrete: A five-phase mesoscale model approach. Constr. Build. Mater. 2019, 197, 587–596. [Google Scholar] [CrossRef]
- Song, G.; Wang, C.; Wang, B. Structural Health Monitoring (SHM) of Civil Structures. Appl. Sci. 2017, 7, 789. [Google Scholar] [CrossRef]
- Yang, Y.W.; Divsholi, B.S.; Soh, C.K. A reusable PZT transducer for monitoring initial hydration and structural health of concrete. Sensors 2010, 10, 5193–5208. [Google Scholar] [CrossRef] [PubMed]
- Huo, L.S.; Wang, F.R.; Li, H.N.; Song, G. A fractal contact theory based model for bolted connection looseness monitoring using piezoceramic transducers. Smart Mater. Struct. 2017, 26, 104010. [Google Scholar] [CrossRef]
- Lu, G.T.; Li, Y.R.; Zhou, M.L.; Feng, Q.; Song, G. Detecting Damage Size and Shape in a Plate Structure Using PZT Transducer Array. J. Aerosp. Eng. 2018, 31, 04018075. [Google Scholar] [CrossRef]
- Huo, L.S.; Li, C.B.; Jiang, T.Y.; Li, H.N. Feasibility Study of Steel Bar Corrosion Monitoring Using a Piezoceramic Transducer Enabled Time Reversal Method. Appl. Sci. 2018, 8, 2304. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.Q.; Hao, H.; Ou, J.P. Guided wave propagation and spectral element method for debonding damage assessment in RC structures. J. Sound Vib. 2009, 324, 751–772. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Zhang, L.Y.; Liu, L.J.; Huo, L.S. Prestress monitoring of a steel strand in an anchorage connection using piezoceramic transducers and time reversal method. Appl. Sci. 2018, 18, 4018. [Google Scholar] [CrossRef] [PubMed]
- Du, G.F.; Kong, Q.Z.; Zhou, H.; Gu, H.C. Multiple cracks detection in pipeline using damage index matrix based on piezoceramic transducer-enabled stress wave propagation. Sensors 2017, 17, 1812. [Google Scholar] [CrossRef] [PubMed]
- Venugopal, V.P.; Wang, G. Modeling and analysis of Lamb wave propagation in a beam under Lead Zirconate Titanate actuation and sensing. J. Intell. Mater. Syst. Struct. 2015, 26, 1679–1698. [Google Scholar] [CrossRef]
- Wang, F.R.; Huo, L.S.; Song, G. A piezoelectric active sensing method for quantitative monitoring of bolt loosening using energy dissipation caused by tangential damping based on the fractal contact theory. Smart Mater. Struct. 2018, 27, 9. [Google Scholar] [CrossRef]
- Xu, K.; Deng, Q.S.; Cai, L.J.; Ho, S.H.; Song, G. Damage Detection of a Concrete Column Subject to Blast Loads Using Embedded Piezoceramic Transducers. Sensors 2018, 18, 1377. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.Y.; Wang, T.; Yang, D.; Liu, S.P.; Shao, J.H.; Li, Y.R. A Smart Washer for Bolt Looseness Monitoring Based on Piezoelectric Active Sensing Method. Appl. Sci. 2016, 6, 320. [Google Scholar] [CrossRef]
- Shao, J.H.; Wang, T.; Yin, H.Y.; Yang, D.; Li, Y.R. Bolt Looseness Detection Based on Piezoelectric Impedance Frequency Shift. Appl. Sci. 2016, 6, 298. [Google Scholar] [CrossRef]
- Wang, F.R.; Ho, S.C.M.; Huo, L.S.; Song, G. A Novel Fractal Contact-Electromechanical Impedance Model for Quantitative Monitoring of Bolted Joint Looseness. IEEE Access 2018, 6, 40212–40220. [Google Scholar] [CrossRef]
- Xu, J.; Wang, C.Y.; Li, H.G.; Zhang, C.W.; Hao, J.J.; Fan, S.L. Health Monitoring of Bolted Spherical Joint Connection Based on Active Sensing Technique Using Piezoceramic Transducers. Sensors 2018, 18, 1727. [Google Scholar] [CrossRef] [PubMed]
- Provdakis, C.P.; Stefanaki, K.D.; Voutetaki, M.E.; Tsompanakis, Y.; Stavroulaki, M. Damage detection in concrete structures using a simultaneously activated multi-mode PZT active sensing system: Numerical modelling. Struct. Infrastr. Eng. 2014, 10, 1451–1468. [Google Scholar] [CrossRef]
- Jiang, T.Y.; Kong, Q.Z.; Wang, W.X.; Huo, L.S. Monitoring of grouting compactness in a post-tensioning tendon duct using piezoceramic transducers. Sensors 2016, 16, 1343. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Li, B.; Song, G. Active debonding detection for large rectangular CFSTs based on wavelet packet energy spectrum with piezoceramics. J. Struct. Eng. 2013, 139, 1435–1443. [Google Scholar] [CrossRef]
- Luo, M.Z.; Li, W.J.; Hei, C.; Song, G. Concrete infill monitoring in concrete-filled FRP tubes using a PZT-based ultrasonic time-of-flight method. Sensors 2016, 16, 2083. [Google Scholar] [CrossRef] [PubMed]
- Kong, Q.Z.; Feng, Q.; Song, G. Water presence detection in a concrete crack using smart aggregates. Int. Smart Nano Mater. 2015, 6, 149–161. [Google Scholar] [CrossRef] [Green Version]
- Kong, Q.Z.; Robert, R.; Silva, P.; Mo, Y.L. Cyclic crack monitoring of a reinforced concrete column under simulated pseudo-dynamic loading using piezoceramic-based smart aggregates. Appl. Sci. 2016, 6, 341. [Google Scholar] [CrossRef]
- Gu, H.C.; Moslehy, Y.; Sanders, D.; Song, G. Multi-functional smart aggregate-based structural health monitoring of circular reinforced concrete columns subjected to seismic excitations. Smart Mater Struct. 2010, 19, 065026. [Google Scholar] [CrossRef]
- Li, W.J.; Kong, Q.Z.; Ho, S.C.M.; Lim, I. Feasibility study of using smart aggregates as embedded acoustic emission sensors for health monitoring of concrete structures. Smart Mater. Struct. 2016, 25, 115031. [Google Scholar] [CrossRef]
- Wang, J.J.; Kong, Q.Z.; Shi, Z.F.; Song, G. Electromechanical properties of smart aggregate: Theoretical modeling and experimental validation. Smart Mater. Struct. 2016, 25, 095008. [Google Scholar] [CrossRef]
- Hong, X.B.; Wang, H.; Wang, T.; Liu, G.X. Dynamic cooperative identification based on synergetics for pipe structural health monitoring with piezoceramic transducers. Smart Mater. Struct. 2013, 22, 045003. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, T.; Gu, H.; Gu, H.H. Active interface debonding detection of a concrete-filled steel tube with piezoelectric technologies using wavelet packet analysis. Mech. Syst. Sign. Proc. 2013, 36, 7–17. [Google Scholar] [CrossRef]
- Huang, Q.; Xu, B.; Li, B.; Song, G. Monitoring for large cross-section CFSTs of a super high-rise building with piezoceramic actuators and sensors. Adv. Mater. Res. 2011, 163–167, 7. [Google Scholar] [CrossRef]
- Du, G.F.; Zhang, J.; Zhang, J.C.; Song, G. Experimental study on stress monitoring of sand-filled steel tube during impact using piezoceramic smart aggregates. Sensors 2017, 17, 1930. [Google Scholar] [CrossRef] [PubMed]
- Kong, Q.Z.; Fan, S.L.; Bai, X.L.; Mo, Y.L.; Song, G. A novel embeddable spherical smart aggregate for structural health monitoring: Part I. Fabrication and electrical characterization. Smart Mater. Struct. 2017, 26, 8. [Google Scholar] [CrossRef]
- Kong, Q.Z.; Fan, S.L.; Mo, Y.L.; Song, G. A novel embeddable spherical smart aggregate for structural health monitoring: Part II. numerical and experimental verifications. Smart Mater. Struct. 2017, 26. [Google Scholar] [CrossRef]
- Soh, C.K.; Tseng, K.K.; Bhalla, S.; Gupta, A. Performance of smart piezoceramic patches in health monitoring of a RC bridge. Smart Mater. Struct. 2000, 9, 533. [Google Scholar] [CrossRef]
- Tsai, K.C.; Wu, S.; Popve, E.P. Cyclic performance of steel beam-column moment joints. Eng. Struct. 1995, 17, 596–602. [Google Scholar] [CrossRef]
- Mitra, N. Pinching4 Model (OpenSees User Documentation); University of California: Oakland, CA, USA, 2012. [Google Scholar]
- Federico, G.; Maurizio, O.; Paolo, S. Pinching in Steel Rack Joints: Numerical Modelling and Effects on Structural Response. Int. J. Steel Struct. 2019, 19, 131–146. [Google Scholar]



























| Member | Section-Size (mm) |
|---|---|
| infill plate | 1850 × 1400 × 2.5 |
| frame beam | H100 × 50 × 4.5 × 3.2 |
| left and right columns | H150 × 150 × 4 × 6 |
| Item | Forward Loading | Reverse Loading | ||||
|---|---|---|---|---|---|---|
| (kN/mm) | (kN) | (kN) | (kN/mm) | (kN) | (kN) | |
| Experiment | 40.38 | 535.5 | 516.2 | 39.94 | −506.5 | −468.0 |
| Finite Element | 42.89 | 502.0 | 502.0 | 43.28 | −508.4 | −466.2 |
| Difference (%) | 6.22 | −6.67 | −2.83 | 8.36 | 0.38 | −0.39 |
| Specimens Number | Peak of Point A (kN) | Displacement of Point A (mm) | Inter Story Drift of Point A | Peak of Point C (kN) | Displacement of Point C (mm) | Inter Story Drift of Point C | Lateral Stiffness (kN/mm) |
|---|---|---|---|---|---|---|---|
| S1t1.5 | 518 | 5.02 | 3.35 × 10−3 | 590.5 | 51.78 | 3.45 × 10−2 | 103.19 |
| S1t2.0 | 685.5 | 4.48 | 2.99 × 10−3 | 736.2 | 44.99 | 3.00 × 10−2 | 153.01 |
| S1t2.5 | 816.4 | 4.47 | 2.98 × 10−3 | 930.6 | 46.8 | 3.12 × 10−2 | 182.64 |
| S1t3.0 | 962.6 | 3.96 | 2.64 × 10−3 | 1104.9 | 47.7 | 3.18 × 10−2 | 243.08 |
| S1t3.5 | 1105.3 | 3.95 | 2.63 × 10−3 | 1419 | 50.26 | 3.35 × 10−2 | 279.82 |
| S1t4.0 | 1232.7 | 3.95 | 2.63 × 10−3 | 1622.7 | 53.83 | 3.59 × 10−2 | 312.08 |
| S1t4.5 | 1358.5 | 3.95 | 2.63 × 10−3 | 1761.5 | 52.5 | 3.50 × 10−2 | 343.92 |
| S1t5.0 | 1480.6 | 3.95 | 2.63 × 10−3 | 1962.1 | 53.82 | 3.59 × 10−2 | 374.84 |
| Specimens Number | SABC+SCDA Area (kN·mm) | SOBE+SODF Area (kN·mm) | Energy Dissipation Coefficient E |
|---|---|---|---|
| S1t1.5 | 63,360 | 28,800 | 2.2 |
| S1t2.0 | 80,640 | 25,040 | 3.5 |
| S1t2.5 | 128,510 | 33,600 | 3.82 |
| S1t3.0 | 135,640 | 35,120 | 3.86 |
| S1t3.5 | 157,840 | 39,840 | 3.96 |
| S1t4.0 | 170,640 | 38,400 | 4.44 |
| S1t4.5 | 202,640 | 44,280 | 4.57 |
| S1t5.0 | 221,920 | 47,550 | 4.67 |
| Specimens Number | Grade of Concrete | Axial Compression Ratio u | Plate Thickness |
|---|---|---|---|
| S1C30 | C30 | 0.3 | 2.5 mm |
| S1C40 | C40 | 0.3 | 2.5 mm |
| S1C50 | C50 | 0.3 | 2.5 mm |
| S1C60 | C60 | 0.3 | 2.5 mm |
| S1C70 | C70 | 0.3 | 2.5 mm |
| S1C80 | C80 | 0.3 | 2.5 mm |
| Specimens Number | Peak of Point A (kN) | Displacement of Point A (mm) | Inter Story Drift of Point A | Peak of Point C (kN) | Displacement of Point C (mm) | Inter Story Drift of Point C | Lateral Stiffness (kN/mm) |
|---|---|---|---|---|---|---|---|
| S1C30 | 816.4 | 4.47 | 2.98 × 10−3 | 930.6 | 46.8 | 3.12 × 10−2 | 182.64 |
| S1C40 | 823.3 | 4.47 | 2.98 × 10−3 | 951.8 | 46.8 | 3.12 × 10−2 | 184.18 |
| S1C50 | 823.1 | 4.47 | 2.98 × 10−3 | 955.5 | 46.8 | 3.12 × 10−2 | 184.14 |
| S1C60 | 823.8 | 4.47 | 2.98 × 10−3 | 985.2 | 46.8 | 3.12 × 10−2 | 184.3 |
| S1C70 | 826.7 | 4.47 | 2.98 × 10−3 | 971.2 | 46.8 | 3.12 × 10−2 | 184.94 |
| S1C80 | 824.3 | 3.96 | 2.64 × 10−3 | 970.3 | 45.9 | 3.06 × 10−2 | 208.16 |
| Specimens Number | SABC+SCDA Area (kN·mm) | SOBE+SODF Area (kN·mm) | Energy Dissipation Coefficient E |
|---|---|---|---|
| S1C30 | 128,510 | 33,600 | 3.82 |
| S1C40 | 129,120 | 33,780 | 3.82 |
| S1C50 | 129,740 | 33,850 | 3.83 |
| Specimens Number | Grade of Concrete | Axial Compression Ratio u | Plate Thickness |
|---|---|---|---|
| S1μ0 | C30 | 0 | 2.5 mm |
| S1μ02 | C30 | 0.2 | 2.5 mm |
| S1μ03 | C30 | 0.3 | 2.5 mm |
| S1μ04 | C30 | 0.4 | 2.5 mm |
| S1μ05 | C30 | 0.5 | 2.5 mm |
| S1μ06 | C30 | 0.6 | 2.5 mm |
| Specimens Number | Peak of Point A (kN) | Displacement of Point A (mm) | Inter Story Drift of Point A | Peak of Point C (kN) | Displacement of Point C (mm) | Inter Story Drift of Point C | Lateral Stiffness (kN/mm) |
|---|---|---|---|---|---|---|---|
| S1μ0 | 813 | 4.47 | 2.98 × 10−3 | 971.9 | 47.7 | 3.18 × 10−2 | 181.88 |
| S1μ02 | 825.3 | 4.47 | 2.98 × 10−3 | 942.7 | 46.8 | 3.12 × 10−2 | 184.63 |
| S1μ03 | 816.4 | 4.47 | 2.98 × 10−3 | 930.6 | 46.8 | 3.12 × 10−2 | 182.64 |
| S1μ04 | 821.5 | 4.47 | 2.98 × 10−3 | 921.8 | 47.7 | 3.18 × 10−2 | 183.78 |
| S1μ05 | 817.7 | 4.46 | 2.97 × 10−3 | 910.2 | 50.3 | 3.35 × 10−2 | 183.34 |
| S1μ06 | 817 | 4.46 | 2.87 × 10−3 | 850.5 | 47.7 | 3.18 × 10−2 | 183.18 |
| Specimens Number | SABC+SCDA Area (kN·mm) | SOBE + SODF Area (kN·mm) | Energy Dissipation Coefficient E |
|---|---|---|---|
| S1μ0 | 129,440 | 33,392 | 3.87 |
| S1μ02 | 128,540 | 33,476 | 3.84 |
| S1μ03 | 128,510 | 33,600 | 3.82 |
| S1μ04 | 128,540 | 34,360 | 3.66 |
| S1μ05 | 125,680 | 36,370 | 3.46 |
| S1μ06 | 170,640 | 36,640 | 3.41 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Zhang, H.; Yang, W. Study on Seismic Performance and Damage Analysis of Steel Plate Shear Wall with Partially Encased Composite (PEC) Columns. Appl. Sci. 2019, 9, 907. https://doi.org/10.3390/app9050907
Yin Z, Zhang H, Yang W. Study on Seismic Performance and Damage Analysis of Steel Plate Shear Wall with Partially Encased Composite (PEC) Columns. Applied Sciences. 2019; 9(5):907. https://doi.org/10.3390/app9050907
Chicago/Turabian StyleYin, Zhanzhong, Hui Zhang, and Wenwei Yang. 2019. "Study on Seismic Performance and Damage Analysis of Steel Plate Shear Wall with Partially Encased Composite (PEC) Columns" Applied Sciences 9, no. 5: 907. https://doi.org/10.3390/app9050907
APA StyleYin, Z., Zhang, H., & Yang, W. (2019). Study on Seismic Performance and Damage Analysis of Steel Plate Shear Wall with Partially Encased Composite (PEC) Columns. Applied Sciences, 9(5), 907. https://doi.org/10.3390/app9050907