Nonuniform Bessel-Based Radiation Distributions on A Spherically Curved Boundary for Modeling the Acoustic Field of Focused Ultrasound Transducers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Measurement Setup
2.2. Acoustic Field Modeling Using FEM
2.2.1. Radiator with Uniform Vibration Distribution
2.2.2. Radiator with “Classical” Nonuniform Vibration
2.2.3. Radiator with Bessel Acceleration
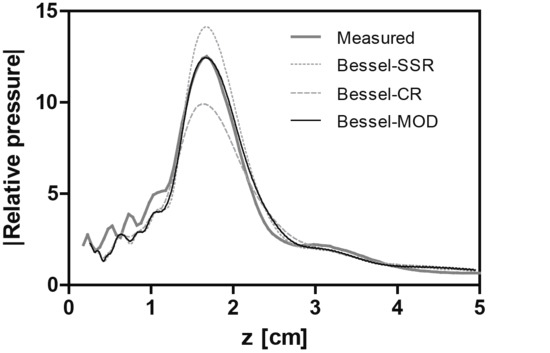
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bystritsky, A.; Korb, A.S.; Douglas, P.K.; Cohen, M.S.; Melega, W.P.; Mulgaonkar, A.P.; DeSalles, A.; Min, B.-K.; Yoo, S.-S. A review of low-intensity focused ultrasound pulsation. Brain Stimul. 2011, 4, 125–136. [Google Scholar] [CrossRef] [PubMed]
- Miller, D.L.; Smith, N.B.; Bailey, M.R.; Czarnota, G.J.; Hynynen, K.; Makin, I.R.S.; Bioeffects Committee of American Institute of Ultrasound in Medicine. Overview of Therapeutic Ultrasound Applications and Safety Considerations. J. Ultrasound Med. 2012, 31, 623–634. [Google Scholar] [CrossRef] [PubMed]
- Diederich, C.J.; Hynynen, K. Ultrasound technology for hyperthermia. Ultrasound Med. Biol. 1999, 25, 871–887. [Google Scholar] [PubMed]
- Huang, T.-H.; Tang, C.-H.; Chen, H.-I.; Fu, W.-M.; Yang, R.-S. Low-Intensity Pulsed Ultrasound-Promoted Bone Healing Is Not Entirely Cyclooxgenase 2 Dependent. J. Ultrasound Med. 2008, 27, 1415–1423. [Google Scholar] [CrossRef] [PubMed]
- Fishman, P.S.; Frenkel, V. Focused Ultrasound: An Emerging Therapeutic Modality for Neurologic Disease. Neurotherapeutics 2017, 14, 393–404. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y. Generation of uniform lesions in high intensity focused ultrasound ablation. Ultrasonics 2013, 53, 495–505. [Google Scholar] [CrossRef] [PubMed]
- Hynynen, K.; Roemer, R.; Anhalt, D.; Johnson, C.; Xu, Z.X.; Swindell, W.; Cetas, T. A scanned, focused, multiple transducer ultrasonic system for localized hyperthermia treatments. 1987. Int. J. Hyperth. 2010, 26, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Jung, Y.J.; Kim, R.; Ham, H.-J.; Park, S.I.; Lee, M.Y.; Kim, J.; Hwang, J.; Park, M.-S.; Yoo, S.-S.; Maeng, L.-S.; et al. Focused low-intensity pulsed ultrasound enhances bone regeneration in rat calvarial bone defect through enhancement of cell proliferation. Ultrasound Med. Biol. 2015, 41, 999–1007. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Tian, Z.; Wan, M. Bioeffects of Low-Intensity Ultrasound In Vitro. J. Ultrasound Med. 2010, 29, 963–974. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, V. Ultrasound mediated delivery of drugs and genes to solid tumors. Adv. Drug Deliv. Rev. 2008, 60, 1193–1208. [Google Scholar] [CrossRef] [PubMed]
- Hynynen, K. Ultrasound for drug and gene delivery to the brain. Adv. Drug Deliv. Rev. 2008, 60, 1209–1217. [Google Scholar] [CrossRef] [PubMed]
- Jenne, J.W.; Preusser, T.; Günther, M. High-intensity focused ultrasound: Principles, therapy guidance, simulations and applications. Z. Med. Phys. 2012, 22, 311–322. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, T.; Ohtsuka, H.; Arimura, N.; Sonoda, S.; Kato, C.; Ushimaru, K.; Hara, N.; Tachibana, K.; Sakamoto, T. Sonothrombolysis for intraocular fibrin formation in an animal model. Ultrasound Med. Biol. 2009, 35, 1845–1853. [Google Scholar] [CrossRef] [PubMed]
- Arora, D.; Cooley, D.; Perry, T.; Skliar, M.; Roemer, R.B. Direct thermal dose control of constrained focused ultrasound treatments: Phantom and in vivo evaluation. Phys. Med. Biol. 2005, 50, 1919–1935. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Hu, P.; Li, X.; Jeong, H. Calibration of focused circular transducers using a multi-Gaussian beam model. Appl. Acoust. 2018, 133, 182–185. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Jeong, H.; Cho, S. Calibration of focused ultrasonic transducers and absolute measurements of fluid nonlinearity with diffraction and attenuation corrections. J. Acoust. Soc. Am. 2017, 142, 984–990. [Google Scholar] [CrossRef] [PubMed]
- Cathignol, D.; Sapozhnikov, O.A.; Zhang, J. Lamb waves in piezoelectric focused radiator as a reason for discrepancy between O’Neil’s formula and experiment. J. Acoust. Soc. Am. 1997, 101, 1286–1297. [Google Scholar] [CrossRef]
- Rosnitskiy, P.B.; Yuldashev, P.V.; Sapozhnikov, O.A.; Maxwell, A.D.; Kreider, W.; Bailey, M.R.; Khokhlova, V.A. Design of HIFU Transducers for Generating Specified Nonlinear Ultrasound Fields. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 374–390. [Google Scholar] [CrossRef] [PubMed]
- Nell, D.M.; Myers, M.R. Thermal effects generated by high-intensity focused ultrasound beams at normal incidence to a bone surface. J. Acoust. Soc. Am. 2010, 127, 549–559. [Google Scholar] [CrossRef] [PubMed]
- O’Neil, H.T. Theory of Focusing Radiators. J. Acoust. Soc. Am. 1949, 21, 516–526. [Google Scholar] [CrossRef]
- Sapozhnikov, O.A.; Pishchal’nikov, Y.A.; Morozov, A.V. Reconstruction of the normal velocity distribution on the surface of an ultrasonic transducer from the acoustic pressure measured on a reference surface. Acoust. Phys. 2003, 49, 354–360. [Google Scholar] [CrossRef]
- Lucas, B.G.; Muir, T.G. The field of a focusing source. J. Acoust. Soc. Am. 1982, 72, 1289–1296. [Google Scholar] [CrossRef]
- Baboux, J.C.; Lakestani, F.; Perdrix, M. Theoretical and experimental study of the contribution of radial modes to the pulsed ultrasonic field radiated by a thick piezoelectric disk. J. Acoust. Soc. Am. 1984, 75, 1722–1731. [Google Scholar] [CrossRef]
- Maréchal, P.; Levassort, F.; Tran-Huu-Hue, L.-P.; Lethiecq, M. Effect of Radial Displacement of Lens on Response of Focused Ultrasonic Transducer. Jpn. J. Appl. Phys. 2007, 46, 3077–3085. [Google Scholar] [CrossRef]
- Riera-Franco de Sarabia, E.; Ramos-Fernandez, A.; Rodriguez-Lopez, F. Temporal evolution of transient transverse beam profiles in near-field zones. Ultrasonics 1994, 32, 47–56. [Google Scholar] [CrossRef]
- Laura, P.A. Directional Characteristics of Vibrating Circular Plates and Membranes. J. Acoust. Soc. Am. 1966, 40, 1031–1033. [Google Scholar] [CrossRef]
- Gutierrez, M.I.; Calas, H.; Ramos, A.; Vera, A.; Leija, L. Acoustic Field Modeling for Physiotherapy Ultrasound Applicators by Using Approximated Functions of Measured Non-Uniform Radiation Distributions. Ultrasonics 2012, 52, 767–777. [Google Scholar] [PubMed]
- Delannoy, B.; Bruneel, C.; Lasota, H.; Ghazaleh, M. Theoretical and Experimental-Study of the Lamb Wave Eigenmodes of Vibration in Terms of the Transducer Thickness to Width Ratio. J. Appl. Phys. 1981, 52, 7433–7438. [Google Scholar] [CrossRef]
- Canney, M.S.; Bailey, M.R.; Crum, L.A.; Khokhlova, V.A.; Sapozhnikov, O.A. Acoustic characterization of high intensity focused ultrasound fields: A combined measurement and modeling approach. J. Acoust. Soc. Am. 2008, 124, 2406–2420. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.B.; Moros, E.G.; Straube, W.L. Ultrasound field estimation method using a secondary source-array numerically constructed from a limited number of pressure measurements. J. Acoust. Soc. Am. 2000, 107, 3259–3265. [Google Scholar] [CrossRef] [PubMed]
- Dekker, D.L.; Piziali, R.L.; Dong, E. Effect of Boundary-Conditions on Ultrasonic-Beam Characteristics of Circular Disks. J. Acoust. Soc. Am. 1974, 56, 87–93. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez, M.I.; Lopez-Haro, S.A.; Vera, A.; Leija, L. Experimental Verification of Modeled Thermal Distribution Produced by a Piston Source in Physiotherapy Ultrasound. Biomed. Res. Int. 2016, 2016, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Rayleigh, L. The Theory of Sound; Dover Publications: New York, NY, USA, 1945. [Google Scholar]
- Khokhlova, V.A.; Souchon, R.; Tavakkoli, J.; Sapozhnikov, O.A.; Cathignol, D. Numerical modeling of finite-amplitude sound beams: Shock formation in the near field of a cw plane piston source. J. Acoust. Soc. Am. 2001, 110, 95–108. [Google Scholar] [CrossRef]
- Sapozhnikov, O.A.; Khokhlova, V.A.; Cathignol, D. Nonlinear waveform distortion and shock formation in the near field of a continuous wave piston source. J. Acoust. Soc. Am. 2004, 115, 1982–1987. [Google Scholar] [CrossRef]
- Chapelon, J.-Y.; Cathignol, D.; Cain, C.; Ebbini, E.; Kluiwstra, J.-U.; Sapozhnikov, O.A.; Fleury, G.; Berriet, R.; Chupin, L.; Guey, J.-L. New piezoelectric transducers for therapeutic ultrasound. Ultrasound Med. Biol. 2000, 26, 153–159. [Google Scholar] [CrossRef]
- Miner, G.W.; Laura, P.A. Calculation of Nearfield Pressure Induced by Vibrating Circular Plates. J. Acoust. Soc. Am. 1967, 42, 1025–1030. [Google Scholar] [CrossRef]
- Thomas, O.; Bilbao, S. Geometrically nonlinear flexural vibrations of plates: In-plane boundary conditions and some symmetry properties. J. Sound Vib. 2008, 315, 569–590. [Google Scholar] [CrossRef]
- Guo, N.; Cawley, P. Transient-Response of Piezoelectric Disks to Applied Voltage Pulses. Ultrasonics 1991, 29, 208–217. [Google Scholar] [CrossRef]
- Shaw, E.A.G. On the Resonant Vibrations of Thick Barium Titanate Disks. J. Acoust. Soc. Am. 1956, 28, 38–50. [Google Scholar] [CrossRef]
- Gutierrez, M.I.; Vera, A.; Leija, L.; Ramos, A.; Gutierrez, J. Acoustic field modeling of focused ultrasound transducers using non-uniform radiation distributions. In Proceedings of the 2017 14th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 20–22 September 2017; pp. 1–4. [Google Scholar]
- Marechal, P.; Levassort, F.; Tran-Huu-Hue, L.P.; Lethiecq, M. Electro-acoustic response at the focal point of a focused transducer as a function of the acoustical properties of the lens. In Proceedings of the World Congress on Ultrasonics 2003, Paris, France, 7–10 September 2003; pp. 535–538. [Google Scholar]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutierrez, M.I.; Ramos, A.; Gutierrez, J.; Vera, A.; Leija, L. Nonuniform Bessel-Based Radiation Distributions on A Spherically Curved Boundary for Modeling the Acoustic Field of Focused Ultrasound Transducers. Appl. Sci. 2019, 9, 911. https://doi.org/10.3390/app9050911
Gutierrez MI, Ramos A, Gutierrez J, Vera A, Leija L. Nonuniform Bessel-Based Radiation Distributions on A Spherically Curved Boundary for Modeling the Acoustic Field of Focused Ultrasound Transducers. Applied Sciences. 2019; 9(5):911. https://doi.org/10.3390/app9050911
Chicago/Turabian StyleGutierrez, Mario Ibrahin, Antonio Ramos, Josefina Gutierrez, Arturo Vera, and Lorenzo Leija. 2019. "Nonuniform Bessel-Based Radiation Distributions on A Spherically Curved Boundary for Modeling the Acoustic Field of Focused Ultrasound Transducers" Applied Sciences 9, no. 5: 911. https://doi.org/10.3390/app9050911
APA StyleGutierrez, M. I., Ramos, A., Gutierrez, J., Vera, A., & Leija, L. (2019). Nonuniform Bessel-Based Radiation Distributions on A Spherically Curved Boundary for Modeling the Acoustic Field of Focused Ultrasound Transducers. Applied Sciences, 9(5), 911. https://doi.org/10.3390/app9050911