Theoretical Study of the Iron Complexes with Aminoguanidine: Investigating Secondary Antioxidant Activity
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Complexes of Fe(III) with Protonated AG
3.2. Complexes of Fe(III) with AG
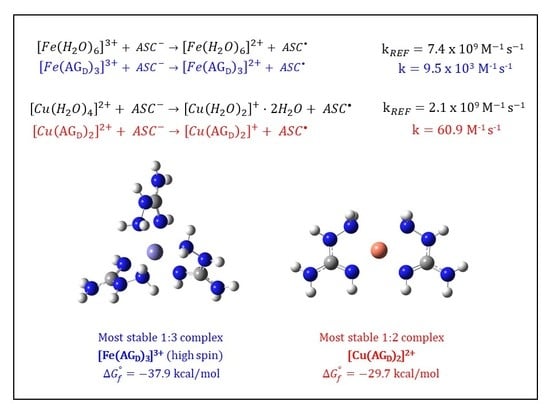
3.3. Kinetic Calculations for the Reduction of Fe(III): Comparison with the Cu(II)/Cu(I) Reduction
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thorpe, S.R.; Baynes, J.W. Maillard reaction products in tissue proteins: New products and new perspectives. Amino Acids 2003, 25, 275–281. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, P.; Cerami, A. Protein glycation, diabetes, and aging. Recent Prog. Horm. Res. 2001, 56, 1–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Münch, G.; Mayer, S.; Michaelis, J.; Hipkiss, A.R.; Riederer, P.; Müller, R.; Neumann, A.; Schinzel, R.; Cunningham, A.M. Influenced of advanced glycation end-products and AGE-inhibitors on nucleation-dependent polymerization of beta-amyloid peptide. Biochim. Biophys. Acta 1997, 1360, 17–29. [Google Scholar] [CrossRef] [Green Version]
- Stitt, A.W. The maillard reaction in eye diseases. Ann. N. Y. Acad. Sci. 2005, 1043, 582–597. [Google Scholar] [CrossRef] [Green Version]
- Colzani, M.; De Maddis, D.; Casali, G.; Carini, M.; Vistoli, G.; Aldini, G. Reactivity, selectivity, and reaction mechanisms of aminoguanidine, hydralazine, pyridoxamine, and carnosine as sequestering agents of reactive carbonyl species: A comparative study. Chem. Med. Chem. 2016, 11, 1778–1789. [Google Scholar] [CrossRef]
- Haber, F.; Weiss, J. On the catalyst of hydroperoxide. Naturwissenschaften 1932, 20, 948–950. [Google Scholar] [CrossRef]
- Zhao, M.J.; Jung, L. Kinetics of the competitive degradation of deoxyribose and other molecules by hydroxyl radicals produced by the fenton reaction in the presence of ascorbic acid. Free Radic. Res. 1995, 23, 229–243. [Google Scholar] [CrossRef]
- Burkitt, M.J.; Gilbert, B.C. Model studies of the iron-catalysed haber-weiss cycle and the ascorbate-driven fenton reaction. Free Radic. Res. Commun. 1990, 10, 265–280. [Google Scholar] [CrossRef]
- Price, D.L.; Rhett, P.M.; Thorpe, S.R.; Baynes, J.W. Chelating activity of advanced glycation end-products inhibitors. J. Biol. Chem. 2001, 276, 48967–48972. [Google Scholar] [CrossRef] [Green Version]
- Rahbar, S.; Natarajan, R.; Yerneni, K.K.; Scott, S.; Gonzales, N.; Nadler, J.L. Evidence that pioglitazone, metformin and pentoxifylline are inhibitors of glycation. Clin. Chim. Acta 2000, 301, 65–77. [Google Scholar] [CrossRef]
- Ortega-Castro, J.; Adrover, M.; Frau, J.; Donoso, J.; Muñoz, F. Chelating power of LR-74, a new AGE-inhibitor. Chem. Phys. Lett. 2008, 465, 120–125. [Google Scholar] [CrossRef]
- Casasnovas, R.; Ortega-Castro, J.; Donoso, J.; Frau, F.; Muñoz, F. Theoretical calculations of stability constants and pKa values of metal complexes in solution: Application to pyridoxamine-copper(II) complexes and their biological implications in AGE inhibition. Phys. Chem. Chem. Phys. 2013, 15, 16303–16313. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Rahman, E.; Bolton, W.K. Pimagedine: A novel therapy for diabetic nephropathy. Expert Opin. Investig. Drugs 2002, 11, 565–574. [Google Scholar]
- Li, Y.M.; Steffes, M.; Donnelly, T.; Liu, C.; Fuh, H.; Basgen, J.; Bucala, R.; Vlassara, H. Prevention of cardiovascular and renal pathology of aging by the advanced glycation inhibitor aminoguanidine. Proc. Natl. Acad. Sci. USA 1996, 93, 3902–3907. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ortega-Castro, J.; Frau, J.; Casasnovas, R.; Fernández, D.; Donoso, J.; Muñoz, F. High- and low-spin Fe(III) complexes of various AGE inhibitors. J. Phys. Chem. A 2012, 116, 2961–2971. [Google Scholar] [CrossRef]
- Ortega-Castro, J.; Adrover, M.; Frau, J.; Donoso, J.; Muñoz, F. Cu2+ complexes of some AGEs inhibitors. Chem. Phys. Lett. 2009, 475, 277–284. [Google Scholar] [CrossRef]
- Ortega-Castro, J.; Adrover, M.; Frau, J.; Salvà, A.; Donoso, J.; Muñoz, F. DFT studies on schiff base formation of vitamin B6 analogues. Reaction between a pyridoxamine-analogue and carbonyl compounds. J. Phys. Chem. A 2010, 114, 4634–4640. [Google Scholar] [CrossRef]
- Adrover, M.; Vilanova, B.; Muñoz, F.; Donoso, J. Pyridxamine, a scavenger agent of carbohydrates. Int. J. Chem. Kinet. 2007, 39, 154–167. [Google Scholar] [CrossRef]
- Adrover, M.; Vilanova, B.; Muñoz, F.; Donoso, J. Inhibition of glycosylation processes: The reaction between pyridoxamine and glucose. Chem. Biodivers. 2005, 2, 964–975. [Google Scholar] [CrossRef]
- Solís-Calero, C.; Ortega-Castro, J.; Frau, J.; Muñoz, F. Scavenger mechanism of methylglyoxal by metformin. A DFT study. Theor. Chem. Acc. 2015, 134, 48–62. [Google Scholar] [CrossRef]
- Rahbar, S.; Figarola, J.L. Novel inhibitors of advanced glycation endproducts. Arch. Biochem. Biophys. 2003, 419, 63–79. [Google Scholar] [CrossRef] [PubMed]
- Ramis, R.; Casasnovas, R.; Mariño, L.; Frau, J.; Adrover, M.; Vilanova, B.; Mora-Diez, N.; Ortega-Castro, J. A density functional theory study of the free-radical scavenging activity of aminoguanidine. Comparison with its reactive carbonyl compound and metal scavenging activities. Int. J. Quantum Chem. 2019, 119, e25911. [Google Scholar] [CrossRef]
- García-Díez, G.; Ramis, R.; Mora-Diez, N. Theoretical study of the copper complexes with aminoguanidine: Investigating secondary antioxidant activity. ACS Omega 2020, 5, 14502–14512. [Google Scholar] [CrossRef] [PubMed]
- Monreal-Corona, R.; Ippolito, A.A.; Biddlecombe, J.R.; Mora-Diez, N. Theoretical study of the iron complexes with lipoic and dihydrolipoic acids: Exploring secondary antioxidant activity. Antioxidants 2020, 9, 674. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09, Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Exchange-correlation functional with broad accuracy for metallic and non-metallic compounds, kinetics, and noncovalent interactions. J. Chem. Phys. 2005, 123, 161103–161106. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functional for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition metals: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Marcus, R.A. Electrons transfer reactions in chemistry. Theory and experiment. Rev. Mod. Phys. 1993, 65, 599–610. [Google Scholar] [CrossRef] [Green Version]
- Marcus, R.A. Transfer reactions in chemistry. Theory and experiment. Pure Appl. Chem. 1997, 69, 13–30. [Google Scholar] [CrossRef]
- Collins, F.C.; Kimball, G.E. Diffusion-controlled reaction rates. J. Colloid. Sci. 1949, 4, 425–437. [Google Scholar] [CrossRef]
- Smoluchowskim, M.Z. Versuch einer mathematischen theorie der koagulationskinetik kolloider Lösungen. J. Phys. Chem. 1917, 92, 129–168. [Google Scholar]
- Einstein, A. Über die von der molekularkinetischen theorie der wärme geforderte bewegung von in ruhenden flüssigkeiten suspendierten teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef] [Green Version]
- Stokes, G.G. Mathematical and Physical Papers; Cambridge University Press: Cambridge, UK, 1903; Volume 3. [Google Scholar]
- Castañeda-Arriaga, R.; Alvarez-Idaboy, J.R.; Mora-Diez, N. Theoretical study of copper complexes with lipoic and dihydrolipoic acids. RSC Adv. 2016, 6, 107924–107932. [Google Scholar] [CrossRef]
- Castañeda-Arriaga, R.; Mora-Diez, N.; Alvarez-Idaboy, J.R. Modelling the chemical repair of protein carbon-centered radicals formed via oxidative damage with dihydrolipoic acid. RCS Adv. 2015, 5, 96714–96719. [Google Scholar] [CrossRef]
- Castañeda-Arriaga, R.; Domínguez-Casto, A.; Lee, J.; Alvarez-Idaboy, J.R.; Mora-Diez, N. Chemical repair of protein-centred radicals: Long-distance dynamic factors. Can. J. Chem. 2016, 94, 1119–1126. [Google Scholar] [CrossRef]
- Ramis, R.; Casasnovas, R.; Ortega-Castro, J.; Frau, J.; Alvarez-Idaboy, J.R.; Mora-Diez, N. Modelling the repair of carbon-centered protein radicals by the antioxidants glutathione and Trolox. New J. Chem. 2019, 43, 2085–2097. [Google Scholar] [CrossRef]
- Galano, A.; Alvarez-Idaboy, J.R. A computational methodology for accurate predictions of rate constants in solution: Application to the assessment of primary antioxidant activity. J. Comput. Chem. 2013, 34, 2430–2445. [Google Scholar] [CrossRef]
- Romeo, I.; Parise, A.; Galano, A.; Russo, N.; Alvarez-Idaboy, J.R.; Marino, T. The antioxidant capability of higenamine: Insights from theory. Antioxidants 2020, 9, 358. [Google Scholar] [CrossRef]
- Goel, S.; Masunov, A.E. Pairwise spin-contamination correction method and dft study of mnh and h2 dissociation curves. In Computational Science—ICCS 2009; Allen, G., Nabrzyski, J., Seidel, E., van Albada, G.D., Dongarra, J., Sloot, P.M.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5545. [Google Scholar]
- Koskinen, M.; Mutikainen, I.; Tilus, P.; Pelttari, E.; Korvela, M.; Elo, H. Structure of aminoguanidine hemioxalate. Implications for the synthesis of amidinohydrazones. Mon. Chem. 1997, 128, 767–775. [Google Scholar] [CrossRef]
- Greenwood, N.N.; Earnshaw, A. Chemistry of the Elements, 2nd ed.; Butterworth-Heinemann: Leeds, UK, 1997. [Google Scholar]
- Edler, E.; Stein, M. Spin-state-dependent properties of an Iron(III) hydrogenase mimic. Eur. J. Inorg. Chem. 2014, 22, 3587–3599. [Google Scholar] [CrossRef] [Green Version]
- Boldyrev, V.V.; Tukhtaev, R.K.; Gavrilov, A.I.; Larionov, S.V.; Savel’eva, Z.A.; Lavrenova, L.G. Combustion of nickel and copper nitrate complexes of hydrazine derivatives as a method for manufacturing fine-grained and porous metals. Russ. J. Inorg. Chem. 1998, 43, 302–305. [Google Scholar]
- Buettner, G.G. Ascorbate autoxidation in the presence of iron and copper chelates. Free Rad. Res. Commun. 1986, 1, 349–353. [Google Scholar] [CrossRef] [PubMed]
- Francisco-Marquez, M.; Aguilar-Fernánde, M.; Galano, A. Anthranilic acid as a secondary antioxidant: Implications to the inhibition of OH production and the associated oxidative stress. Comp. Theor. Chem. 2016, 1077, 18–24. [Google Scholar] [CrossRef]
- Martínez, A.; Vargas, R.; Galano, A. Citric acid: A promising copper scavenger. Comp. Theor. Chem. 2018, 1133, 47–50. [Google Scholar] [CrossRef]
- Castañeda-Arriaga, R.; Pérez-González, A.; Reina, M.; Alvarez-Idaboy, J.R.; Galano, A. Comprehensive investigation of the antioxidant and pro-oxidant effects of phenolic compounds: A double-edged sword in the context of oxidative stress? J. Phys. Chem. B 2018, 122, 6198–6214. [Google Scholar] [CrossRef] [PubMed]
- Mravljak, J.; Jakopin, Z. Iron-binding and anti-fenton properties of novel amino acid-derived cyclic imide dioximes. Antioxidants 2019, 8, 473. [Google Scholar] [CrossRef] [Green Version]
- Kubicova, L.; Hadacek, F.; Bachmann, G.; Weckwerth, W.; Chobot, V. Coordination complex formation and redox properties of kynurenic and xanthurenic acid can affect brain tissue homeodynamics. Antioxidants 2019, 8, 476. [Google Scholar] [CrossRef] [Green Version]
- Brovč, E.V.; Pajk, S.; Šink, R.; Mravljak, J. Protein formulations containing polysorbates: Are metal chelators needed at all? Antioxidants 2020, 9, 441. [Google Scholar] [CrossRef]
- Wang, L.; Santos, E.; Schenk, D.; Rabago-Smith, M. Kinetics and mechanistic studies on the reaction between cytochrome c and tea catechins. Antioxidants 2014, 3, 559–568. [Google Scholar] [CrossRef]
- Guerreiro, J.F.; Gomes, M.A.G.B.; Pagliari, F.; Jansen, J.; Marafioti, M.G.; Nistico, C.; Hanley, R.; Costa, R.O.; Ferreira, S.S.; Mendes, F.; et al. Iron and copper complexes with antioxidant activity as inhibitors of the metastatic potential of glioma cells. RSC Adv. 2020, 10, 12699–12710. [Google Scholar] [CrossRef]
- Bielski, B.H.J.; Cabelli, D.E.; Arudi, R.L.; Ross, A.B. Reactivity of HO2/O−2 radicals in aqueous solution. J. Phys. Chem. Ref. Data 1985, 14, 1041–1100. [Google Scholar] [CrossRef]






| Complex | |||
|---|---|---|---|
| {14} [Fe(AGD)3]3+ hs (N2, N4) | −36.8 | 9.03 × 1026 | 26.96 |
| {15} [Fe(AGD)3]3+ ls (N2, N4) | −6.7 | 8.22 × 104 | 4.91 |
| {16} [Fe(AGD)3]3+ hs (same orientation, N2, N4) | −37.9 | 5.65 × 1027 | 27.75 |
| {17} [Fe(AGD)3(H2O)]3+ hs (N2, N4, N2′, N4′, N2′) | −24.1 | 4.96 × 1017 | 17.70 |
| {18} [Fe(AGD)3(H2O)2]3+ hs (N2, N4, N2′, N2′) | −19.1 | 1.03 × 1014 | 14.01 |
| {32} [Fe(AGD)2(H2O)2]3+ hs (trans, N2, N4) | −20.1 | 5.35 × 1014 | 14.73 |
| {34} [Fe(AGD)2(H2O)2]3+ hs (mirror image, N2, N4) | −19.0 | 7.91 × 1013 | 13.90 |
| {38} [Fe(AGD)2(H2O)2]3+ hs (cis, N2, N4) | −22.9 | 5.86 × 1016 | 16.77 |
| {43} [Fe(AGD)(H2O)4]3+ hs (N2, N4) | −10.3 | 3.48 × 107 | 7.54 |
| {49} [Fe(AGA)2(H2O)2]3+ hs (4-coord., N2) | −19.6 | 2.20 × 1014 | 14.34 |
| {51} [Fe(AGB)2(H2O)2]3+ hs (4-coord., N2) | −21.6 | 6.35 × 1015 | 15.80 |
| {54} [Fe(AGC)2(H2O)2]3+ hs (4-coord., N2) | −20.5 | 1.09 × 1015 | 15.04 |
| {57} [Fe(AGD)(H2O)3]3+ hs (5-coord., sq. pyr., N2, N4) | −15.3 | 1.63 × 1011 | 11.21 |
| {59} [Fe(AGD)2]3+ hs (4-coord., N2, N4) | −20.5 | 1.02 × 1015 | 15.01 |
| {60} [Fe(AGD)2(H2O)]3+ hs (5-coord., N2, N4) | −23.5 | 1.78 × 1017 | 17.25 |
| Reaction | kapp | Ratio | kapp | Ratio |
|---|---|---|---|---|
| 7.28 × 109 | 7.43 × 109 | |||
| {15} {61} + (ls) | 7.76 × 109 | 0.94 | 4.48 | 1.66 × 109 |
| {16} {62} + | 8.09 × 109 | 0.90 | 9.47 × 103 | 7.85 × 105 |
| {14} {63} + | 8.29 × 109 | 0.88 | 1.96 × 105 | 3.79 × 104 |
| {17} {64} + | 8.30 × 109 | 0.88 | 1.53 × 108 | 48.6 |
| {38} {65} + | 8.08 × 109 | 0.90 | 6.57 × 108 | 11.3 |
| 7.71 × 109 | 2.10 × 109 | |||
| 2.80 × 109 | 2.75 | 60.9 | 3.45 × 107 | |
| 3.49 × 109 | 2.21 | 66.6 | 3.15 × 107 | |
| 7.02 × 109 | 1.10 | 3.56 × 104 | 5.90 × 104 | |
| 7.40 × 109 | 1.04 | 8.01 × 104 | 2.62 × 104 | |
| 7.47 × 109 | 1.03 | 4.83 × 105 | 4.35 × 103 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Díez, G.; Mora-Diez, N. Theoretical Study of the Iron Complexes with Aminoguanidine: Investigating Secondary Antioxidant Activity. Antioxidants 2020, 9, 756. https://doi.org/10.3390/antiox9080756
García-Díez G, Mora-Diez N. Theoretical Study of the Iron Complexes with Aminoguanidine: Investigating Secondary Antioxidant Activity. Antioxidants. 2020; 9(8):756. https://doi.org/10.3390/antiox9080756
Chicago/Turabian StyleGarcía-Díez, Guillermo, and Nelaine Mora-Diez. 2020. "Theoretical Study of the Iron Complexes with Aminoguanidine: Investigating Secondary Antioxidant Activity" Antioxidants 9, no. 8: 756. https://doi.org/10.3390/antiox9080756
APA StyleGarcía-Díez, G., & Mora-Diez, N. (2020). Theoretical Study of the Iron Complexes with Aminoguanidine: Investigating Secondary Antioxidant Activity. Antioxidants, 9(8), 756. https://doi.org/10.3390/antiox9080756