Modelling the Proton-Conductive Membrane in Practical Polymer Electrolyte Membrane Fuel Cell (PEMFC) Simulation: A Review
Abstract
:1. Introduction
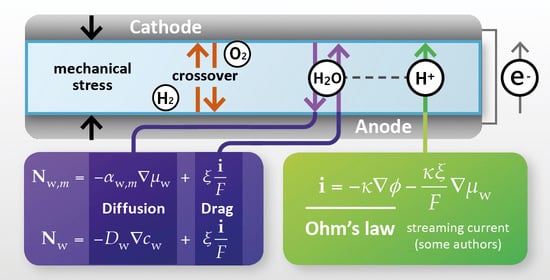
2. Proton-Exchange Membrane: Role and Essential Transport Phenomena
2.1. Role of the Membrane
2.2. Membrane Types and Fundamental Material Properties
2.3. Essential Transport Phenomena in the Membrane
- charge;
- proton mass;
- water mass.
- proton flux (current density);
- water flux.
- momentum (flow/mechanical stress, discussed in Section 7);
- heat (discussed in Section 9);
- dilute dissolved gas mass, to account for gas crossover (discussed in Section 10.1);
- dissolved ion mass (other than protons, discussed in Section 10.2).
3. Charge Transport-Only Membrane Models
3.1. Zero-Dimensional (0D, Lumped) Resistance Models
3.2. Constant Hydration Models
4. Sorption of Water
4.1. Sorption Isotherms
4.2. Empirical Sorption Models for Nafion 1100
4.3. Detailed Sorption Models
4.4. Sorption within the Catalyst Layer
5. Coupled Proton-Water Transport
- proton conductivity κ—the ratio of current density to electrolyte potential gradient for uniform water content;
- electroosmotic drag coefficient ξ—the ratio of water flux to current density for uniform water content;
- water diffusivity Dw—the ratio of water flux to water concentration gradient for zero current density.
- membrane-phase electrolyte potential φ as the thermodynamic variable conjugate to the driving force for current flow, under uniform hydration;
- chemical potential of water μw (expressed as required in terms of the local water content λ) as the thermodynamic variable conjugate to the driving force for water flux, at zero proton current.
5.1. Springer Membrane Model
5.2. Weber–Newman Membrane Model
5.3. Binary Friction Model (BFM)
5.4. Proton Conductivity as a Function of Water Content
5.5. Water Diffusivity as a Function of Water Content
5.6. Electroosmotic Drag Coefficient
5.7. Water Transport: Liquid-Equilibrated Conditions
6. Interface-Specific Phenomena
6.1. Interfacial Proton Transport Resistance
6.2. Interfacial Water Transport Resistance: Vapour-Equilibrated Conditions
6.3. Interfacial Water Transport Resistance: Liquid-Equilibrated Conditions
7. Mechanical Phenomena
7.1. Hydraulic Transport of Water (Flow)
7.2. Membrane Expansion and Mechanical Constraint
8. Transient Response of the Membrane
9. Non-Isothermal Phenomena
10. Transport of Other Chemical Species
10.1. Dilute Gas Transport
10.2. Transport of Other Ions
11. Membrane Degradation
11.1. Mechanical Degradation Models
11.2. Chemical Degradation Models
12. Perspective
- The composite nature of reinforced membranes, including its effect on conductivity, diffusivity, water uptake, and mechanical coupling to transport phenomena.
- The introduction of radical scavengers or other membrane ‘additives’.
- Parameterisation at relevant operating conditions (>60 °C), as opposed to at ambient conditions.
- The impact of variations in different membrane chemistries/side-chain length.
- The use of very thin membranes (<50 μm).
- In-plane inhomogeneities in electrode profiles.
13. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Abbreviation | Definition |
|---|---|
| BET | Brunauer–Emmett–Teller |
| BFM | binary friction model |
| CL | catalyst layer |
| DEFC | direct ethanol fuel cell |
| DMFC | direct methanol fuel cell |
| EIS | electrochemical impedance spectroscopy |
| ePTFE | expanded polytetrafluoroethylene |
| GAB | Guggenheim–Anderson–de Boer |
| GDL | gas diffusion layer |
| IEC | ion-exchange capacity |
| LE | liquid-equilibrated |
| MEA | membrane-electrode assembly |
| MPL | microporous layer |
| MRI | magnetic resonance imaging |
| NMR | nuclear magnetic resonance |
| PEM | polymer electrolyte membrane |
| PEMFC | polymer electrolyte membrane fuel cell |
| PEMWE | polymer electrolyte membrane water electrolyser |
| PFSA | perfluorosulfonic acid |
| VE | vapour-equilibrated |
| Symbol | Unit | Definition |
|---|---|---|
| Ak | 1 | Empirical coefficient, binary friction model |
| Acat | V | Tafel slope (cathode) |
| Adeg | m2 | Degraded area |
| ak | various | Polynomial coefficients, various models |
| apore | m−1 | Effective pore surface area per unit volume, Choi–Datta sorption isotherm |
| avol | m−1 | Volumetric surface area, membrane-vapour contact in CL |
| aw,vap | 1 | Activity, water vapour in gas phase |
| aw | 1 | Activity, sorbed water |
| bk | various | Coefficients, various models |
| cf | mol m−3 | Sulfonic acid group concentration |
| cside-chain | mol m−3 | Side chain concentration, Quiroga degradation model |
| cw | mol m−3 | Concentration, sorbed water |
| Di | m2 s−1 | Fick’s law diffusion coefficient, dilute species i |
| Dcap | kg m−1 s−1 | Capillary diffusion coefficient |
| Dw | m2 s−1 | Fick’s law diffusion coefficient, sorbed water |
| Dw,T | kg m−1 s−1 K−1 | Thermal diffusion coefficient |
| Dλ | m2 s−1 | Effective diffusion coefficient with respect to water content gradient, sorbed water |
| Dμ | m2 s−1 | Self-diffusion coefficient, sorbed water |
| Dμ,WN | m2 s−1 | Self-diffusion coefficient, sorbed water (binary Weber-Newman definition) |
| EA,m | J mol−1 | Activation energy, process m |
| Ecell | V | Cell voltage |
| EOCV | V | Open-circuit cell voltage |
| Emn | kg mol−1 | Empirical coefficients, Meyers sorption isotherm |
| F | C mol−1 | Faraday constant |
| f | 1 | Mazumder diffusion function |
| feff | 1 | Membrane porosity, binary friction model |
| ∆Hm | J mol−1 | Enthalpy change, process m |
| i | A m−2 | Current density |
| ifar | A m−2 | Equivalent current density of proton flux from faradaic reaction |
| icell | A m−2 | Cell current density |
| iref | A m−2 | Reference current density |
| Ka,mem | mol m−3 | Acidity constant, sulfonic acid groups |
| Kdrag | 1 | Phenomenological ratio of water flux to proton flux |
| KH,i | Pa m3 mol−1 | Henry’s law coefficient, species i |
| Kmem | Pa−1 | Langmuir equilibrium constant, Mashio sorption isotherm |
| K1 | 1 | Empirical coefficient, Thampan BET isotherm / Meyers sorption isotherm |
| K2 | 1 | Empirical coefficient, Meyers isotherm |
| k | W m−1 K−1 | Thermal conductivity |
| kbond | s−1 | Water bonding rate constant, Meng water uptake model |
| kdeg | various | Degradation rate constant |
| kG | 1 | Empirical coefficient, Klika GAB isotherm |
| kint | m s−1 | Interfacial water transport coefficient |
| kvol | s−1 | Interfacial water transport coefficient (volumetric) |
| kvap | s m−2 kg−1 | Sorption rate constant, Meng model |
| Lmem | m | Membrane thickness |
| MEW | kg mol−1 | Equivalent weight (polymer mass per 1 mol sulfonic acid groups) |
| Mw | kg mol−1 | Molar mass, water |
| mw | kg | Mass of water in reference volume V |
| Nw | mol m−2 s−1 | Molar flux, sorbed water |
| N+ | mol m−2 s−1 | Molar flux, protons |
| ni | mol | Content of species in reference volume V |
| ncond | 1 | Scaling exponent with water content, proton conductivity |
| nw,sat | 1 | Empirical coefficient, Thampan BET isotherm |
| p | Pa | Pressure |
| pi,k | Pa | Partial pressure, species i in phase k |
| p0 | Pa | Reference pressure |
| pL | Pa | Absolute pressure in liquid phase |
| psat | Pa | Saturation vapour pressure (water) |
| pw,vap | Pa | Partial pressure, water vapour in gas phase |
| Q | W m−3 | Volumetric heat source |
| q | W m−2 | Heat flux |
| q | 1 | Empirical coefficient, binary friction model |
| RΩ | Ω | Ohmic cell series resistance |
| R | J K−1 mol−1 | Gas constant |
| Rw | kg m−3 s−1 | Liquid water source |
| rcrit | m | Critical maximum/minimum radius of liquid saturation |
| rhole | m | Pinhole radius |
| SL | 1 | Fraction of available membrane channels expanded by liquid water |
| s | 1 | Empirical coefficient, binary friction model |
| T | K | Temperature |
| T0 | K | Reference temperature |
| t | s | Time |
| Uano | V | Anode operating potential |
| V | m3 | Reference volume |
| V(r) | m−1 | Relative volume probability distribution function |
| Vdry | m3 | Reference volume, dry conditions |
| m3 mol−1 | Molar volume, hydrated membrane | |
| m3 mol−1 | Molar volume, sulfonic acid groups | |
| m3 mol−1 | Molar volume, sorbed water | |
| Ymem | Pa | Young’s modulus, membrane |
| zi | 1 | Charge number, species i |
| α | 1 | Net number of water molecules transferred per proton |
| αλ | 1 | Empirical coefficient, Setzler–Fuller conductivity model |
| αw | mol2 m−1 s−1 J−1 | Diffusion coefficient, Weber–Newman model |
| β | 1 | Scaling coefficient, Meyers isotherm |
| βw | 1 | Swelling coefficient, water sorption |
| γw | N m−1 | Surface tension, water-gas interface |
| εij | 1 | Strain tensor |
| εdeg | 1 | Void proportion of degraded membrane |
| θc | 1 | Contact angle of water-gas interface in membrane |
| θm | K | Characteristic temperature, process m |
| κ | S m−1 | Proton conductivity |
| κp | m2 | Permeability |
| κsorp | Pa | Pore elasticity, Choi–Datta sorption isotherm |
| κk | S m−1 | Proton conductivity, equilibration condition k |
| κϕ | m2 | Electroosmotic permeability, Schlögl equation |
| κ0 | S m−1 | Proton conductivity, reference conditions |
| λ | 1 | Water content |
| λcrit | 1 | Critical water content, electroosmotic drag models |
| λeq | 1 | Water content, at equilibrium with a defined water activity |
| λeq,crit | 1 | Critical water content, Meyers isotherm |
| λeq,L | 1 | Water content, liquid-equilibrated conditions |
| λeq,V | 1 | Water content, vapour-equilibrated conditions |
| λmax,k | 1 | Maximum water content, equilibration condition k, Weber–Newman model |
| λmin | 1 | Minimum water content, binary friction model |
| λmono | 1 | Water content, effective monolayer |
| λsat | 1 | Saturated water content |
| λ+ | 1 | Proton content |
| λ0 | 1 | Reference water content |
| μ | Pa s | Dynamic viscosity, sorbed water |
| μw | J mol−1 | Chemical potential, sorbed water |
| ξ | 1 | Electroosmotic drag coefficient |
| ρ | kg m−3 | Membrane density |
| ρdry | kg m−3 | Membrane density (dry conditions) |
| ρw | kg m−3 | Density of sorbed water |
| ϕ | V | Electrolyte potential, membrane phase |
| ϕm | 1 | Effective membrane volume fraction, Flory–Huggins model |
| ϕw | 1 | Water volume fraction, membrane phase |
| ϕw,crit | 1 | Critical volume fraction, Weber–Newman conductivity model |
| ϕw,max | 1 | Conductivity-maximum volume fraction, Weber–Newman conductivity model |
| ϕk | 1 | Empirical coefficient, Meyers isotherm |
| χ | 1 | Flory–Huggins parameter |
| χc | 1 | Degree of constraint, Weber membrane mechanical model |
| ψi | mol m−1 s−1 Pa−1 | Permeation coefficient, species i |
| ω | 1 | Empirical coefficient, Kosakian conductivity model |
References
- Kusoglu, A.; Weber, A.Z. New Insights into Perfluorinated Sulfonic-Acid lonomers. Chem. Rev. 2017, 117, 987–1104. [Google Scholar] [CrossRef]
- Kreuer, K.D.; Paddison, S.J.; Spohr, E.; Schuster, M. Transport in proton conductors for fuel-cell applications: Simulations, elementary reactions, and phenomenology. Chem. Rev. 2004, 104, 4637–4678. [Google Scholar] [CrossRef] [Green Version]
- Hickner, M.A.; Pivovar, B.S. The chemical and structural nature of proton exchange membrane fuel cell properties. Fuel Cells 2005, 5, 213–229. [Google Scholar] [CrossRef]
- Peighambardoust, S.J.; Rowshanzamir, S.; Amjadi, M. Review of the proton exchange membranes for fuel cell applications. Int. J. Hydrogen Energy 2010, 35, 9349–9384. [Google Scholar] [CrossRef]
- Yuan, X.-Z.; Wang, H. PEM Fuel Cell Fundamentals. In PEM Fuel Cell Electrocatalysts and Catalyst Layers: Fundamentals and Applications; Zhang, J., Ed.; Springer: London, UK, 2008; pp. 1–87. [Google Scholar]
- Andreaus, B.; Eikerling, M. Catalyst Layer Operation in PEM Fuel Cells: From Structural Pictures to Tractable Models. In Device and Materials Modeling in PEM Fuel Cells; Paddison, S.J., Promislow, K.S., Eds.; Springer: New York, NY, USA, 2009; pp. 41–90. [Google Scholar]
- Weber, A.Z.; Borup, R.L.; Darling, R.M.; Das, P.K.; Dursch, T.J.; Gu, W.B.; Harvey, D.; Kusoglu, A.; Litster, S.; Mench, M.M.; et al. A Critical Review of Modeling Transport Phenomena in Polymer-Electrolyte Fuel Cells. J. Electrochem. Soc. 2014, 161, F1254–F1299. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Li, Z.; Zhang, J.B. Review of characterization and modeling of polymer electrolyte fuel cell catalyst layer: The blessing and curse of ionomer. Front. Energy 2017, 11, 334–364. [Google Scholar] [CrossRef]
- Weber, A.Z.; Newman, J. Modeling transport in polymer-electrolyte fuel cells. Chem. Rev. 2004, 104, 4679–4726. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X.G. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Nasef, M.M.; Aly, A.A. Water and charge transport models in proton exchange membranes: An overview. Desalination 2012, 287, 238–246. [Google Scholar] [CrossRef]
- Zamel, N.; Li, X.G. Effective transport properties for polymer electrolyte membrane fuel cells - With a focus on the gas diffusion layer. Prog. Energy Combust. Sci. 2013, 39, 111–146. [Google Scholar] [CrossRef]
- Balasubramanian, S.; Weber, A.Z. Continuum, Macroscopic Modeling of Polymer-Electrolyte Fuel Cells. In Physical Multiscale Modeling and Numerical Simulation of Electrochemical Devices for Energy Conversion and Storage: From Theory to Engineering to Practice; Franco, A.A., Doublet, M.L., Bessler, W.G., Eds.; Springer: London, UK, 2016; pp. 91–149. [Google Scholar]
- Costamagna, P. Transport phenomena in polymeric membrane fuel cells. Chem. Eng. Sci. 2001, 56, 323–332. [Google Scholar] [CrossRef]
- Smitha, B.; Sridhar, S.; Khan, A.A. Solid polymer electrolyte membranes for fuel cell applications—A review. J. Membr. Sci. 2005, 259, 10–26. [Google Scholar] [CrossRef]
- Zaton, M.; Roziere, J.; Jones, D.J. Current understanding of chemical degradation mechanisms of perfluorosulfonic acid membranes and their mitigation strategies: A review. Sustain. Energy Fuels 2017, 1, 409–438. [Google Scholar] [CrossRef]
- Gebert, M.; Ghielmi, A.; Merlo, L.; Corasaniti, M.; Arcella, V. AQUIVION(TM)–The Short-Side-Chain and Low-EW PFSA for Next-Generation PEFCs Expands Production and Utilization. ECS Trans. 2010, 26, 279–283. [Google Scholar] [CrossRef]
- Solvay. Available online: https://www.solvay.com/en/brands/aquivion-ion-conducting-polymers (accessed on 20 October 2020).
- Emery, M.; Frey, M.; Guerra, M.; Haugen, G.; Hintzer, K.; Lochhaas, K.H.; Pham, P.; Pierpont, D.; Schaberg, M.; Thaler, A.; et al. The Development of New Membranes for Proton Exchange Membrane Fuel Cells. ECS Trans. 2007, 11, 3–14. [Google Scholar] [CrossRef] [Green Version]
- 3M Company. Available online: https://www.3m.com/3M/en_US/design-and-specialty-materials-us/ionomers/ (accessed on 20 October 2020).
- Penner, R.M.; Martin, C.R. Ion Transporting Composite Membranes: I. Nafion--Impregnated Gore--Tex. J. Electrochem. Soc. 1985, 132, 514–515. [Google Scholar] [CrossRef]
- Bahar, B.; Hobson, A.R.; Kolde, J.A. Integral Composite Membrane. U.S. Patent US5599614A, 4 February 1997. [Google Scholar]
- Endoh, E. Highly Durable MEA for PEMFC Under High Temperature and Low Humidity Conditions. ECS Trans. 2006, 3, 9–18. [Google Scholar] [CrossRef]
- Shi, S.W.; Weber, A.Z.; Kusoglu, A. Structure/property relationship of Nafion XL composite membranes. J. Membr. Sci. 2016, 516, 123–134. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.J.; Tan, J.T.; Zhan, Z.G.; Pan, M. Water transport law of fuel cell membranes at different current densities. Chin. Sci. Bull. Chin. 2019, 64, 2254–2261. [Google Scholar] [CrossRef] [Green Version]
- Yandrasits, M.A.; Lindell, M.J.; Hamrock, S.J. New directions in perfluoroalkyl sulfonic acid-based proton-exchange membranes. Curr. Opin. Electrochem. 2019, 18, 90–98. [Google Scholar] [CrossRef]
- Rolfi, A.; Oldani, C.; Merlo, L.; Facchi, D.; Ruffo, R. New perfluorinated ionomer with improved oxygen permeability for application in cathode polymeric electrolyte membrane fuel cell. J. Power Sources 2018, 396, 95–101. [Google Scholar] [CrossRef]
- Varcoe, J.R.; Atanassov, P.; Dekel, D.R.; Herring, A.M.; Hickner, M.A.; Kohl, P.A.; Kucernak, A.R.; Mustain, W.E.; Nijmeijer, K.; Scott, K.; et al. Anion-exchange membranes in electrochemical energy systems. Energy Environ. Sci. 2014, 7, 3135–3191. [Google Scholar] [CrossRef] [Green Version]
- The Chemours Company FC, LLC. Product Bulletin P-11: Nafion(TM) NR211 and NR212 Ion Exchange Materials: Solution Cast Membranes; The Chemours Company FC, LLC.: Wilmington, DE, USA, 2017. [Google Scholar]
- Thampan, T.; Malhotra, S.; Tang, H.; Datta, R. Modeling of conductive transport in proton-exchange membranes for fuel cells. J. Electrochem. Soc. 2000, 147, 3242–3250. [Google Scholar] [CrossRef]
- Hasan, M.; Goshtasbi, A.; Chen, J.X.; Santare, M.H.; Ersal, T. Model-Based Analysis of PFSA Membrane Mechanical Response to Relative Humidity and Load Cycling in PEM Fuel Cells. J. Electrochem. Soc. 2018, 165, F3359–F3372. [Google Scholar] [CrossRef] [Green Version]
- The Chemours Company FC, LLC. Product Bulletin P-12: Nafion(TM) N115, N117 and N1110 Ion Exchange Materials: Extrusion Cast Membranes; The Chemours Company FC, LLC.: Wilmington, DE, USA, 2016. [Google Scholar]
- Berg, P.; Promislow, K.; St Pierre, J.; Stumper, J.; Wetton, B. Water management in PEM fuel cells. J. Electrochem. Soc. 2004, 151, A341–A353. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.M.; Srinivasan, S.; Chamberlin, C.E. Modeling of Proton Exchange Membrane Fuel Cell Performance with an Empirical Equation. J. Electrochem. Soc. 1995, 142, 2670–2674. [Google Scholar] [CrossRef]
- Gerteisen, D.; Heilmann, T.; Ziegler, C. Modeling the phenomena of dehydration and flooding of a polymer electrolyte membrane fuel cell. J. Power Sources 2009, 187, 165–181. [Google Scholar] [CrossRef]
- Wu, H.; Li, X.G.; Berg, P. On the modeling of water transport in polymer electrolyte membrane fuel cells. Electrochim. Acta 2009, 54, 6913–6927. [Google Scholar] [CrossRef]
- Newman, J.; Tiedemann, W. Porous-electrode theory with battery applications. AIChE J. 1975, 21, 25–41. [Google Scholar] [CrossRef] [Green Version]
- Iden, H.; Sato, K.; Ohma, A.; Shinohara, K. Relationship among Microstructure, Ionomer Property and Proton Transport in Pseudo Catalyst Layers. J. Electrochem. Soc. 2011, 158, B987–B994. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Von Schroeder, P. Über Erstarrungs- und Quellugserscheinungen von Gelatine. Z. Phys. Chem. 1903, 45, 75–117. [Google Scholar] [CrossRef]
- Choi, P.H.; Datta, R. Sorption in proton-exchange membranes—An explanation of Schroeder’s paradox. J. Electrochem. Soc. 2003, 150, E601–E607. [Google Scholar] [CrossRef] [Green Version]
- Weber, A.Z.; Newman, J. Transport in polymer-electrolyte membranes—I. Physical model. J. Electrochem. Soc. 2003, 150, A1008–A1015. [Google Scholar] [CrossRef]
- Freger, V. Hydration of Ionomers and Schroeder’s Paradox in Nafion. J. Phys. Chem. B 2009, 113, 24–36. [Google Scholar] [CrossRef]
- Eikerling, M.H.; Berg, P. Poroelectroelastic theory of water sorption and swelling in polymer electrolyte membranes. Soft Matter 2011, 7, 5976–5990. [Google Scholar] [CrossRef]
- Jeck, S.; Scharfer, P.; Kind, M. Absence of Schroeder’s paradox: Experimental evidence for water-swollen Nafion (R) membranes. J. Membr. Sci. 2011, 373, 74–79. [Google Scholar] [CrossRef]
- Hwang, G.S.; Parkinson, D.Y.; Kusoglu, A.; MacDowell, A.A.; Weber, A.Z. Understanding Water Uptake and Transport in Nafion Using X-ray Microtomography. ACS Macro Lett. 2013, 2, 288–291. [Google Scholar] [CrossRef]
- Bridgeman, O.C.; Aldrich, E.W. Vapor Pressure Tables for Water. J. Heat Transf. 1964, 86, 279–286. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X.G. Three-dimensional multiphase modeling of cold start processes in polymer electrolyte membrane fuel cells. Electrochim. Acta 2009, 54, 6876–6891. [Google Scholar] [CrossRef]
- Gurau, V.; Zawodzinski, T.A.; Mann, J.A. Two-phase transport in PEM fuel cell cathodes. J. Fuel Cell Sci. Technol. 2008, 5. [Google Scholar] [CrossRef]
- Andersson, M.; Beale, S.B.; Espinoza, M.; Wu, Z.; Lehnertbe, W. A review of cell-scale multiphase flow modeling, including water management, in polymer electrolyte fuel cells. Appl. Energy 2016, 180, 757–778. [Google Scholar] [CrossRef]
- Springer, T.E.; Wilson, M.S.; Gottesfeld, S. Modeling and Experimental Diagnostics in Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 1993, 140, 3513–3526. [Google Scholar] [CrossRef]
- Zawodzinski, T.A.; Derouin, C.; Radzinski, S.; Sherman, R.J.; Smith, V.T.; Springer, T.E.; Gottesfeld, S. Water Uptake by and Transport Through Nafion® 117 Membranes. J. Electrochem. Soc. 1993, 140, 1041–1047. [Google Scholar] [CrossRef]
- Zawodzinski, T.A.; Springer, T.E.; Uribe, F.; Gottesfeld, S. Characterization of polymer electrolytes for fuel cell applications. Solid State Ion. 1993, 60, 199–211. [Google Scholar] [CrossRef]
- Broka, K.; Ekdunge, P. Modelling the PEM fuel cell cathode. J. Appl. Electrochem. 1997, 27, 281–289. [Google Scholar] [CrossRef]
- Hinatsu, J.T.; Mizuhata, M.; Takenaka, H. Water Uptake of Perfluorosulfonic Acid Membranes from Liquid Water and Water Vapor. J. Electrochem. Soc. 1994, 141, 1493–1498. [Google Scholar] [CrossRef]
- Pasaogullari, U.; Wang, C.Y.; Chen, K.S. Two-phase transport in polymer electrolyte fuel cells with bilayer cathode gas diffusion media. J. Electrochem. Soc. 2005, 152, A1574–A1582. [Google Scholar] [CrossRef]
- Kulikovsky, A.A. Quasi-3D modeling of water transport in polymer electrolyte fuel cells. J. Electrochem. Soc. 2003, 150, A1432–A1439. [Google Scholar] [CrossRef]
- Meier, F.; Eigenberger, G. Transport parameters for the modelling of water transport in ionomer membranes for PEM-fuel cells. Electrochim. Acta 2004, 49, 1731–1742. [Google Scholar] [CrossRef]
- Karpenko-Jereb, L.; Innerwinkler, P.; Kelterer, A.M.; Sternig, C.; Fink, C.; Prenninger, P.; Tatschl, R. A novel membrane transport model for polymer electrolyte fuel cell simulations. Int. J. Hydrogen Energy 2014, 39, 7077–7088. [Google Scholar] [CrossRef]
- Futerko, P.; Hsing, I.M. Two-dimensional finite-element method study of the resistance of membranes in polymer electrolyte fuel cells. Electrochim. Acta 2000, 45, 1741–1751. [Google Scholar] [CrossRef]
- Morris David, R.; Sun, X. Water-sorption and transport properties of Nafion 117 H. J. Appl. Polym. Sci. 1993, 50, 1445–1452. [Google Scholar] [CrossRef]
- Steinkamp, K.; Schumacher, J.O.; Goldsmith, F.; Ohlberger, M.; Ziegler, C. A nonisothermal PEM fuel cell model including two water transport mechanisms in the membrane. J. Fuel Cell Sci. Technol. 2008, 5. [Google Scholar] [CrossRef]
- Klika, V.; Kubant, J.; Pavelka, M.; Benziger, J.B. Non-equilibrium thermodynamic model of water sorption in Nafion membranes. J. Membr. Sci. 2017, 540, 35–49. [Google Scholar] [CrossRef]
- Meyers, J.P.; Newman, J. Simulation of the Direct Methanol Fuel Cell: I. Thermodynamic Framework for a Multicomponent Membrane. J. Electrochem. Soc. 2002, 149, A710–A717. [Google Scholar] [CrossRef]
- Weber, A.Z.; Newman, J. Transport in polymer-electrolyte membranes—II. Mathematical model. J. Electrochem. Soc. 2004, 151, A311–A325. [Google Scholar] [CrossRef]
- Weber, A.Z.; Newman, J. A Combination Model for Macroscopic Transport in Polymer-Electrolyte Membranes. In Device and Materials Modeling in PEM Fuel Cells; Paddison, S.J., Promislow, K.S., Eds.; Springer: New York, NY, USA, 2009; pp. 157–198. [Google Scholar]
- Murahashi, T.; Naiki, M.; Nishiyama, E. Water transport in the proton exchange-membrane fuel cell: Comparison of model computation and measurements of effective drag. J. Power Sources 2006, 162, 1130–1136. [Google Scholar] [CrossRef]
- Eikerling, M. Water management in cathode catalyst layers of PEM fuel cells—A structure-based model. J. Electrochem. Soc. 2006, 153, E58–E70. [Google Scholar] [CrossRef]
- Kusoglu, A.; Kwong, A.; Clark, K.T.; Gunterman, H.P.; Weber, A.Z. Water Uptake of Fuel-Cell Catalyst Layers. J. Electrochem. Soc. 2012, 159, F530–F535. [Google Scholar] [CrossRef]
- Jung, C.Y.; Yi, S.C. Influence of the water uptake in the catalyst layer for the proton exchange membrane fuel cells. Electrochem. Commun. 2013, 35, 34–37. [Google Scholar] [CrossRef]
- DeCaluwe, S.C.; Baker, A.M.; Bhargava, P.; Fischer, J.E.; Dura, J.A. Structure-property relationships at Nafion thin-film interfaces: Thickness effects on hydration and anisotropic ion transport. Nano Energy 2018, 46, 91–100. [Google Scholar] [CrossRef]
- Mashio, T.; Sato, K.; Ohma, A. Analysis of Water Adsorption and Condensation in Catalyst Layers for Polymer Electrolyte Fuel Cells. Electrochim. Acta 2014, 140, 238–249. [Google Scholar] [CrossRef]
- Kim, T.-H.; Yoo, J.H.; Maiyalagan, T.; Yi, S.-C. Influence of the Nafion agglomerate morphology on the water-uptake behavior and fuel cell performance in the proton exchange membrane fuel cells. Appl. Surf. Sci. 2019, 481, 777–784. [Google Scholar] [CrossRef]
- Morris, D.R.P.; Liu, S.P.; Gonzalez, D.V.; Gostick, J.T. Effect of Water Sorption on the Electronic Conductivity of Porous Polymer Electrolyte Membrane Fuel Cell Catalyst Layers. ACS Appl. Mater. Interfaces 2014, 6, 18609–18618. [Google Scholar] [CrossRef]
- Kosakian, A.; Padilla Urbina, L.; Heaman, A.; Secanell, M. Understanding single-phase water-management signatures in fuel-cell impedance spectra: A numerical study. Electrochim. Acta 2020, 350. [Google Scholar] [CrossRef]
- Fimrite, J.; Struchtrup, H.; Djilali, N. Transport phenomena in polymer electrolyte membranes—I. Modeling framework. J. Electrochem. Soc. 2005, 152, A1804–A1814. [Google Scholar] [CrossRef]
- Fimrite, J.; Carnes, B.; Struchtrup, H.; Djilali, N. Transport phenomena in polymer electrolyte membranes—II. Binary friction membrane model. J. Electrochem. Soc. 2005, 152, A1815–A1823. [Google Scholar] [CrossRef]
- Fimrite, J.; Carnes, B.; Struchtrup, H.; Djilali, N. Coupled Proton and Water Transport in Polymer Electrolyte Membranes. In Device and Materials Modeling in PEM Fuel Cells; Paddison, S.J., Promislow, K.S., Eds.; Springer: New York, NY, USA, 2009; pp. 123–155. [Google Scholar]
- Zawodzinski, T.A.; Neeman, M.; Sillerud, L.O.; Gottesfeld, S. Determination of water diffusion coefficients in perfluorosulfonate ionomeric membranes. J. Phys. Chem. 1991, 95, 6040–6044. [Google Scholar] [CrossRef]
- Zawodzinski, T.A.; Davey, J.; Valerio, J.; Gottesfeld, S. The water content dependence of electro-osmotic drag in proton-conducting polymer electrolytes. Electrochim. Acta 1995, 40, 297–302. [Google Scholar] [CrossRef]
- Fuller, T.F.; Newman, J. Experimental Determination of the Transport Number of Water in Nafion 117 Membrane. J. Electrochem. Soc. 1992, 139, 1332–1337. [Google Scholar] [CrossRef]
- Carnes, B.; Djilali, N. Analysis of coupled proton and water transport in a PEM fuel cell using the binary friction membrane model. Electrochim. Acta 2006, 52, 1038–1052. [Google Scholar] [CrossRef]
- Motupally, S.; Becker, A.J.; Weidner, J.W. Diffusion of water in Nafion 115 membranes. J. Electrochem. Soc. 2000, 147, 3171–3177. [Google Scholar] [CrossRef]
- Shah, A.A.; Kim, G.S.; Gervais, W.; Young, A.; Promislow, K.; Li, J.; Ye, S. The effects of water and microstructure on the performance of polymer electrolyte fuel cells. J. Power Sources 2006, 160, 1251–1268. [Google Scholar] [CrossRef] [Green Version]
- Djilali, N.; Sui, P.C. Transport phenomena in fuel cells: From microscale to macroscale. Int. J. Comput. Fluid Dyn. 2008, 22, 115–133. [Google Scholar] [CrossRef]
- Li, J.Y.; Nemat-Nasser, S. Micromechanical analysis of ionic clustering in Nafion perfluorinated membrane. Mech. Mater. 2000, 32, 303–314. [Google Scholar] [CrossRef] [Green Version]
- Van Bussel, H.P.L.H.; Koene, F.G.H.; Mallant, R.K.A.M. Dynamic model of solid polymer fuel cell water management. J. Power Sources 1998, 71, 218–222. [Google Scholar] [CrossRef]
- Wiezell, K.; Gode, P.; Lindbergh, G. Steady-state and EIS investigations of hydrogen electrodes and membranes in polymer electrolyte fuel cells I. Modeling. J. Electrochem. Soc. 2006, 153, A749–A758. [Google Scholar] [CrossRef]
- Ju, H.C.; Wang, C.Y.; Cleghorn, S.; Beuscher, U. Nonisothermal modeling of polymer electrolyte fuel cells—I. Experimental validation. J. Electrochem. Soc. 2005, 152, A1645–A1653. [Google Scholar] [CrossRef] [Green Version]
- Neubrand, W. Modellbildung und Simulation von Elektromembranverfahren; Logos Verlag Berlin: Berlin, Germany, 1999. [Google Scholar]
- Ramousse, J.; Deseure, J.; Lottin, O.; Didierjean, S.; Maillet, D. Modelling of heat, mass and charge transfer in a PEMFC single cell. J. Power Sources 2005, 145, 416–427. [Google Scholar] [CrossRef]
- Dobson, P.; Lei, C.; Navessin, T.; Secanell, M. Characterization of the PEM Fuel Cell Catalyst Layer Microstructure by Nonlinear Least-Squares Parameter Estimation. J. Electrochem. Soc. 2012, 159, B514–B523. [Google Scholar] [CrossRef]
- Sone, Y.; Ekdunge, P.; Simonsson, D. Proton Conductivity of Nafion 117 as Measured by a Four--Electrode AC Impedance Method. J. Electrochem. Soc. 1996, 143, 1254–1259. [Google Scholar] [CrossRef]
- Baschuk, J.J.; Li, X.G. Modeling of ion and water transport in the polymer electrolyte membrane of PEM fuel cells. Int. J. Hydrogen Energy 2010, 35, 5095–5103. [Google Scholar] [CrossRef]
- Setzler, B.P.; Fuller, T.F. A Physics-Based Impedance Model of Proton Exchange Membrane Fuel Cells Exhibiting Low-Frequency Inductive Loops. J. Electrochem. Soc. 2015, 162, F519–F530. [Google Scholar] [CrossRef]
- Janssen, G.J.M. A phenomenological model of water transport in a proton exchange membrane fuel cell. J. Electrochem. Soc. 2001, 148, A1313–A1323. [Google Scholar] [CrossRef]
- Eikerling, M.; Kharkats, Y.I.; Kornyshev, A.A.; Volfkovich, Y.M. Phenomenological Theory of Electro--osmotic Effect and Water Management in Polymer Electrolyte Proton--Conducting Membranes. J. Electrochem. Soc. 1998, 145, 2684–2699. [Google Scholar] [CrossRef]
- St-Pierre, J. Simple mathematical model for water diffusion in Nafion membranes. J. Electrochem. Soc. 2007, 154, B88–B95. [Google Scholar] [CrossRef]
- Okada, T.; Xie, G.; Tanabe, Y. Theory of water management at the anode side of polymer electrolyte fuel cell membranes. J. Electroanal. Chem. 1996, 413, 49–65. [Google Scholar] [CrossRef]
- Fuller, T.F.; Newman, J. Water and Thermal Management in Solid--Polymer--Electrolyte Fuel Cells. J. Electrochem. Soc. 1993, 140, 1218–1225. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.V.; White, R.E. A Water and Heat Management Model for Proton--Exchange--Membrane Fuel Cells. J. Electrochem. Soc. 1993, 140, 2178–2186. [Google Scholar] [CrossRef]
- Mazumder, S. A generalized phenomenological model and database for the transport of water and current in polymer electrolyte membranes. J. Electrochem. Soc. 2005, 152, A1633–A1644. [Google Scholar] [CrossRef]
- Ye, X.H.; Wang, C.Y. Measurement of water transport properties through membrane-electrode assemblies. J. Electrochem. Soc. 2007, 154, B676–B682. [Google Scholar] [CrossRef]
- Wu, H.; Berg, P.; Li, X.G. Non-isothermal transient modeling of water transport in PEM fuel cells. J. Power Sources 2007, 165, 232–243. [Google Scholar] [CrossRef]
- Pivovar, B.S. An overview of electro-osmosis in fuel cell polymer electrolytes. Polymer 2006, 47, 4194–4202. [Google Scholar] [CrossRef]
- Peng, Z.; Morin, A.; Huguet, P.; Schott, P.; Pauchet, J. In-Situ Measurement of Electroosmotic Drag Coefficient in Nafion Membrane for the PEMFC. J. Phys. Chem. B 2011, 115, 12835–12844. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.H.; McClure, J.P.; Fedkiw, P.S. Transport properties of proton- and hydroxide-exchange membranes for fuel cells. Electrochim. Acta 2012, 79, 126–132. [Google Scholar] [CrossRef]
- Um, S.; Wang, C.Y. Computational study of water transport in proton exchange membrane fuel cells. J. Power Sources 2006, 156, 211–223. [Google Scholar] [CrossRef]
- Ge, S.H.; Yi, B.L.; Ming, P.W. Experimental determination of electro-osmotic drag coefficient in Nafion membrane for fuel cells. J. Electrochem. Soc. 2006, 153, A1443–A1450. [Google Scholar] [CrossRef]
- Ge, S.H.; Li, X.G.; Yi, B.L.; Hsing, I.M. Absorption, desorption, and transport of water in polymer electrolyte membranes for fuel cells. J. Electrochem. Soc. 2005, 152, A1149–A1157. [Google Scholar] [CrossRef]
- Ise, M.; Kreuer, K.D.; Maier, J. Electroosmotic drag in polymer electrolyte membranes: An electrophoretic NMR study. Solid State Ion. 1999, 125, 213–223. [Google Scholar] [CrossRef]
- Benziger, J.B.; Cheah, M.J.; Klika, V.; Pavelka, M. Interfacial Constraints on Water and Proton Transport Across Nafion Membranes. J. Polym. Sci. Part. B-Polym. Phys. 2015, 53, 1580–1589. [Google Scholar] [CrossRef]
- Berning, T. On water transport in polymer electrolyte membranes during the passage of current. Int. J. Hydrogen Energy 2011, 36, 9341–9344. [Google Scholar] [CrossRef]
- Berg, P.; Stornes, M. Towards a Consistent Interpretation of Electro-osmotic Drag in Polymer Electrolyte Membranes. Fuel Cells 2016, 16, 715–724. [Google Scholar] [CrossRef]
- Dreyer, W.; Guhlke, C.; Müller, R. Overcoming the shortcomings of the Nernst-Planck model. Phys. Chem. Chem. Phys. 2013, 15, 7075–7086. [Google Scholar] [CrossRef] [PubMed]
- Bernardi, D.M.; Verbrugge, M.W. Mathematical model of a gas diffusion electrode bonded to a polymer electrolyte. AIChE J. 1991, 37, 1151–1163. [Google Scholar] [CrossRef]
- Pivovar, B.S.; Kim, Y.S. The membrane-electrode interface in PEFCs. J. Electrochem. Soc. 2007, 154, B739–B744. [Google Scholar] [CrossRef]
- Kim, Y.S.; Pivovar, B.S. The Membrane-Electrode Interface in PEFCs IV. The origin and implications of interfacial resistance. J. Electrochem. Soc. 2010, 157, B1616–B1623. [Google Scholar] [CrossRef]
- Tsampas, M.N.; Pikos, A.; Brosda, S.; Katsaounis, A.; Vayenas, C.G. The effect of membrane thickness on the conductivity of Nafion. Electrochim. Acta 2006, 51, 2743–2755. [Google Scholar] [CrossRef]
- Rangel-Cárdenas, A.L.; Koper, G.J.M. Transport in Proton Exchange Membranes for Fuel Cell Applications—A Systematic Non-Equilibrium Approach. Materials 2017, 10, 576. [Google Scholar] [CrossRef] [Green Version]
- Cheah, M.J.; Kevrekidis, I.G.; Benziger, J. Effect of Interfacial Water Transport Resistance on Coupled Proton and Water Transport Across Nafion. J. Phys. Chem. B 2011, 115, 10239–10250. [Google Scholar] [CrossRef] [PubMed]
- Kientiz, B.; Yamada, H.; Nonoyama, N.; Weber, A.Z. Interfacial Water Transport Effects in Proton-Exchange Membranes. J. Fuel Cell Sci. Technol. 2011, 8. [Google Scholar] [CrossRef]
- Um, S.; Wang, C.Y.; Chen, K.S. Computational fluid dynamics modeling of proton exchange membrane fuel cells. J. Electrochem. Soc. 2000, 147, 4485–4493. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.Y. Transient analysis of polymer electrolyte fuel cells. Electrochim. Acta 2005, 50, 1307–1315. [Google Scholar] [CrossRef]
- Meng, H. A three-dimensional PEM fuel cell model with consistent treatment of water transport in MEA. J. Power Sources 2006, 162, 426–435. [Google Scholar] [CrossRef]
- Adachi, M.; Navessin, T.; Xie, Z.; Frisken, B.; Holdcroft, S. Correlation of In Situ and Ex Situ Measurements of Water Permeation Through Nafion NRE211 Proton Exchange Membranes. J. Electrochem. Soc. 2009, 156, B782–B790. [Google Scholar] [CrossRef] [Green Version]
- Yau, T.C.; Cimenti, M.; Bi, X.T.T.; Stumper, J. Water transport and Schroder’s Paradox in fuel cell membrane electrode assemblies. J. Power Sources 2013, 224, 285–289. [Google Scholar] [CrossRef]
- Teranishi, K.; Tsushima, S.; Hirai, S. Analysis of water transport in PEFCs by magnetic resonance imaging measurement. J. Electrochem. Soc. 2006, 153, A664–A668. [Google Scholar] [CrossRef]
- Liu, X.L.; Lou, G.F.; Wen, Z. Three-dimensional two-phase flow model of proton exchange membrane fuel cell with parallel gas distributors. J. Power Sources 2010, 195, 2764–2773. [Google Scholar] [CrossRef]
- Majsztrik, P.W.; Satterfield, M.B.; Bocarsly, A.B.; Benziger, J.B. Water sorption, desorption and transport in Nafion membranes. J. Membr. Sci. 2007, 301, 93–106. [Google Scholar] [CrossRef]
- Davey, J.; Mukundan, R.; Spendelow, J.; Hussey, D.S.; Jacobson, D.; Arif, M.; Borup, R.L. Water Dynamics in a PEM Fuel Cell: Effect of Current and Humidity Transients. ECS Trans. 2008, 16, 329–340. [Google Scholar] [CrossRef]
- Monroe, C.W.; Romero, T.; Merida, W.; Eikerling, M. A vaporization-exchange model for water sorption and flux in Nafion. J. Membr. Sci. 2008, 324, 1–6. [Google Scholar] [CrossRef]
- Gurau, V.; Edwards, R.V.; Mann, J.A.; Zawodzinski, T.A. A look at the multiphase mixture model for PEM fuel cell simulations. Electrochem. Solid State Lett. 2008, 11, B132–B135. [Google Scholar] [CrossRef]
- Berning, T.; Odgaard, M.; Kær, S.K. Water balance simulations of a polymer-electrolyte membrane fuel cell using a two-fluid model. J. Power Sources 2011, 196, 6305–6317. [Google Scholar] [CrossRef]
- Berg, P.; Novruzi, A.; Promislow, K. Analysis of a cathode catalyst layer model for a polymer electrolyte fuel cell. Chem. Eng. Sci. 2006, 61, 4316–4331. [Google Scholar] [CrossRef]
- Satterfield, M.B.; Benziger, J.B. Non-fickian water vapor sorption dynamics by nafion membranes. J. Phys. Chem. B 2008, 112, 3693–3704. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.H.; Kjeang, E. Macroscopic In-Situ Modeling of Chemical Membrane. Degradation in Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 2014, 161, F823–F832. [Google Scholar] [CrossRef]
- Vorobev, A.; Zikanov, O.; Shamim, T. A computational model of a PEM fuel cell with finite vapor absorption rate. J. Power Sources 2007, 166, 92–103. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, C.; Gerteisen, D. Validity of two-phase polymer electrolyte membrane fuel cell models with respect to the gas diffusion layer. J. Power Sources 2009, 188, 184–191. [Google Scholar] [CrossRef]
- Weber, A.Z.; Newman, J. Transport in polymer-electrolyte membranes—III. Model validation in a simple fuel-cell model. J. Electrochem. Soc. 2004, 151, A326–A339. [Google Scholar] [CrossRef]
- Meng, H.; Han, B.; Ruan, B. Numerical modeling of liquid water transport inside and across membrane in PEM fuel cells. Asia-Pac. J. Chem. Eng. 2013, 8, 104–114. [Google Scholar] [CrossRef]
- Bernardi, D.M.; Verbrugge, M.W. A Mathematical Model of the Solid--Polymer--Electrolyte Fuel Cell. J. Electrochem. Soc. 1992, 139, 2477–2491. [Google Scholar] [CrossRef]
- Hwang, G.S.; Kaviany, M.; Nam, J.H.; Kim, M.H.; Son, S.Y. Pore-Water Morphological Transitions in Polymer Electrolyte of a Fuel Cell. J. Electrochem. Soc. 2009, 156, B1192–B1200. [Google Scholar] [CrossRef]
- Falcão, D.S.; Oliveira, V.B.; Rangel, C.M.; Pinho, C.; Pinto, A.M.F.R. Water transport through a PEM fuel cell: A one-dimensional model with heat transfer effects. Chem. Eng. Sci. 2009, 64, 2216–2225. [Google Scholar] [CrossRef] [Green Version]
- Jung, C.Y.; Lee, C.S.; Yi, S.C. Computational analysis of transport phenomena in proton exchange membrane for polymer electrolyte fuel cells. J. Membr. Sci. 2008, 309, 1–6. [Google Scholar] [CrossRef]
- Nam, J.; Chippar, P.; Kim, W.; Ju, H. Numerical analysis of gas crossover effects in polymer electrolyte fuel cells (PEFCs). Appl. Energy 2010, 87, 3699–3709. [Google Scholar] [CrossRef]
- Rama, P.; Chen, R. Polymer Electrolyte Fuel Cell Transport Mechanisms: A Universal Approach to Multilayer Two-Phase Modeling Through the General Transport Equation. J. Fuel Cell Sci. Technol. 2010, 7. [Google Scholar] [CrossRef]
- Weber, A.Z.; Newman, J. A theoretical study of membrane constraint in polymer-electrolyte fuel cells. AIChE J. 2004, 50, 3215–3226. [Google Scholar] [CrossRef]
- Goulet, M.-A.; Arbour, S.; Lauritzen, M.; Kjeang, E. Water sorption and expansion of an ionomer membrane constrained by fuel cell electrodes. J. Power Sources 2015, 274, 94–100. [Google Scholar] [CrossRef]
- Tang, Y.L.; Karlsson, A.M.; Santare, M.H.; Gilbert, M.; Cleghorn, S.; Johnson, W.B. An experimental investigation of humidity and temperature effects on the mechanical properties of perfluorosulfonic acid membrane. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2006, 425, 297–304. [Google Scholar] [CrossRef]
- Tang, Y.L.; Kusoglu, A.; Karlsson, A.M.; Santare, M.H.; Cleghorn, S.; Johnson, W.B. Mechanical properties of a reinforced composite polymer electrolyte membrane and its simulated performance in PEM fuel cells. J. Power Sources 2008, 175, 817–825. [Google Scholar] [CrossRef] [Green Version]
- Kusoglu, A.; Kienitz, B.L.; Weber, A.Z. Understanding the Effects of Compression and Constraints on Water Uptake of Fuel-Cell Membranes. J. Electrochem. Soc. 2011, 158, B1504–B1514. [Google Scholar] [CrossRef]
- Tang, Y.L.; Santare, M.H.; Karlsson, A.M.; Cleghorn, S.; Johnson, W.B. Stresses in proton exchange membranes due to hygro-thermal loading. J. Fuel Cell Sci. Technol. 2006, 3, 119–124. [Google Scholar] [CrossRef] [Green Version]
- Kusoglu, A.; Tang, Y.L.; Lugo, M.; Karlsson, A.M.; Santare, M.H.; Cleghorn, S.; Johnson, W.B. Constitutive response and mechanical properties of PFSA membranes in liquid water. J. Power Sources 2010, 195, 483–492. [Google Scholar] [CrossRef] [Green Version]
- Khattra, N.S.; Karlsson, A.M.; Santare, M.H.; Walsh, P.; Busby, F.C. Effect of time-dependent material properties on the mechanical behavior of PFSA membranes subjected to humidity cycling. J. Power Sources 2012, 214, 365–376. [Google Scholar] [CrossRef] [Green Version]
- Khorasany, R.M.H.; Goulet, M.-A.; Sadeghi Alavijeh, A.; Kjeang, E.; Wang, G.G.; Rajapakse, R.K.N.D. On the constitutive relations for catalyst coated membrane applied to in-situ fuel cell modeling. J. Power Sources 2014, 252, 176–188. [Google Scholar] [CrossRef]
- Futter, G.A.; Gazdzicki, P.; Friedrich, A.; Latz, A.; Jahnke, T. Physical modeling of polymer-electrolyte membrane fuel cells: Understanding water management and impedance spectra. J. Power Sources 2018, 391, 148–161. [Google Scholar] [CrossRef]
- Franco, A.A.; Schott, P.; Jallut, C.; Maschke, B. A multi-scale dynamic mechanistic model for the transient analysis of PEFCs. Fuel Cells 2007, 7, 99–117. [Google Scholar] [CrossRef]
- Shah, A.A.; Kim, G.S.; Sui, P.C.; Harvey, D. Transient non-isothermal model of a polymer electrolyte fuel cell. J. Power Sources 2007, 163, 793–806. [Google Scholar] [CrossRef]
- Ziegler, C.; Yu, H.M.; Schumacher, J.O. Two-phase dynamic modeling of PEMFCs and simulation of cyclo-voltammograms. J. Electrochem. Soc. 2005, 152, A1555–A1567. [Google Scholar] [CrossRef]
- Khandelwal, M.; Mench, M.M. Direct measurement of through-plane thermal conductivity and contact resistance in fuel cell materials. J. Power Sources 2006, 161, 1106–1115. [Google Scholar] [CrossRef]
- Dai, W.; Wang, H.J.; Yuan, X.Z.; Martin, J.J.; Yang, D.J.; Qiao, J.L.; Ma, J.X. A review on water balance in the membrane electrode assembly of proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2009, 34, 9461–9478. [Google Scholar] [CrossRef]
- Kim, S.; Mench, M.M. Investigation of temperature-driven water transport in polymer electrolyte fuel cell: Thermo-osmosis in membranes. J. Membr. Sci. 2009, 328, 113–120. [Google Scholar] [CrossRef]
- Fu, R.S.; Preston, J.S.; Pasaogullari, U.; Shiomi, T.; Miyazaki, S.; Tabuchi, Y.; Hussey, D.S.; Jacobson, D.L. Water Transport Across a Polymer Electrolyte Membrane under Thermal Gradients. J. Electrochem. Soc. 2011, 158, B303–B312. [Google Scholar] [CrossRef] [Green Version]
- Weber, A.Z. Gas-crossover and membrane-pinhole effects in polymer-electrolyte fuel cells. J. Electrochem. Soc. 2008, 155, B521–B531. [Google Scholar] [CrossRef] [Green Version]
- Kundu, S.; Fowler, M.W.; Simon, L.C.; Abouatallah, R.; Beydokhti, N. Degradation analysis and modeling of reinforced catalyst coated membranes operated under OCV conditions. J. Power Sources 2008, 183, 619–628. [Google Scholar] [CrossRef]
- Zhang, J.X.; Gasteiger, H.A.; Gu, W.B. Electrochemical Measurement of the Oxygen Permeation Rate through Polymer Electrolyte Membranes. J. Electrochem. Soc. 2013, 160, F616–F622. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, C.S.; Mukerjee, S. Oxygen permeation studies on alternative proton exchange membranes designed for elevated temperature operation. Electrochim. Acta 2003, 48, 1845–1859. [Google Scholar] [CrossRef]
- Ahluwalia, R.K.; Wang, X. Buildup of nitrogen in direct hydrogen polymer-electrolyte fuel cell stacks. J. Power Sources 2007, 171, 63–71. [Google Scholar] [CrossRef]
- Giacinti Baschetti, M.; Minelli, M.; Catalano, J.; Sarti, G.C. Gas permeation in perflurosulfonated membranes: Influence of temperature and relative humidity. Int. J. Hydrogen Energy 2013, 38, 11973–11982. [Google Scholar] [CrossRef]
- Baik, K.D.; Kim, M.S. Characterization of nitrogen gas crossover through the membrane in proton-exchange membrane fuel cells. Int. J. Hydrogen Energy 2011, 36, 732–739. [Google Scholar] [CrossRef]
- Karpenko-Jereb, L.; Sternig, C.; Fink, C.; Tatschl, R. Membrane degradation model for 3D CFD analysis of fuel cell performance as a function of time. Int. J. Hydrogen Energy 2016, 41, 13644–13656. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.W.; Sui, P.C.; Kumar, S.; Djilali, N. Modelling and simulations of carbon corrosion during operation of a Polymer Electrolyte Membrane fuel cell. Electrochim. Acta 2009, 54, 5583–5592. [Google Scholar] [CrossRef]
- Sundaram, N.; Peppas, N.A. Friction coefficient analysis of multicomponent solute transport through polymer membranes. J. Appl. Polym. Sci. 1996, 60, 95–101. [Google Scholar] [CrossRef]
- Weber, A.Z.; Delacourt, C. Mathematical Modelling of Cation Contamination in a Proton-exchange Membrane. Fuel Cells 2008, 8, 459–465. [Google Scholar] [CrossRef]
- Burlatsky, S.F.; Gummalla, M.; Atrazhev, V.V.; Dmitriev, D.V.; Kuzminyh, N.Y.; Erikhman, N.S. The Dynamics of Platinum Precipitation in an Ion Exchange Membrane. J. Electrochem. Soc. 2011, 158, B322–B330. [Google Scholar] [CrossRef]
- Wong, K.H.; Kjeang, E. Mitigation of Chemical Membrane Degradation in Fuel Cells: Understanding the Effect of Cell Voltage and Iron Ion Redox Cycle. ChemSusChem 2015, 8, 1072–1082. [Google Scholar] [CrossRef] [PubMed]
- Futter, G.A.; Latz, A.; Jahnke, T. Physical modeling of chemical membrane degradation in polymer electrolyte membrane fuel cells: Influence of pressure, relative humidity and cell voltage. J. Power Sources 2019, 410, 78–90. [Google Scholar] [CrossRef]
- U.S. Department of Energy. 3.4. Fuel Cell. In Fuel Cell Technologies Office Multi-Year Research, Development, and Demonstration Plan; U.S. Department of Energy: Washington, DC, USA, 2017. [Google Scholar]
- Qiu, D.K.; Peng, L.F.; Lai, X.M.; Ni, M.; Lehnert, W. Mechanical failure and mitigation strategies for the membrane in a proton exchange membrane fuel cell. Renew. Sustain. Energy Rev. 2019, 113. [Google Scholar] [CrossRef]
- Kim, S.; Khandelwal, M.; Chacko, C.; Mench, M.M. Investigation of the Impact of Interfacial Delamination on Polymer Electrolyte Fuel Cell Performance. J. Electrochem. Soc. 2009, 156, B99–B108. [Google Scholar] [CrossRef]
- Burlatsky, S.F.; Gummalla, M.; O’Neill, J.; Atrazhev, V.V.; Varyukhin, A.N.; Dmitriev, D.V.; Erikhman, N.S. A mathematical model for predicting the life of polymer electrolyte fuel cell membranes subjected to hydration cycling. J. Power Sources 2012, 215, 135–144. [Google Scholar] [CrossRef] [Green Version]
- Atrazhev, V.V.; Astakhova, T.Y.; Dmitriev, D.V.; Erikhman, N.S.; Sultanov, V.I.; Patterson, T.; Burlatsky, S.F. The Model of Stress Distribution in, Polymer Electrolyte Membrane. J. Electrochem. Soc. 2013, 160, F1129–F1137. [Google Scholar] [CrossRef] [Green Version]
- Khorasany, R.M.H.; Singh, Y.; Sadeghi Alavijeh, A.; Rajapakse, R.K.N.D.; Kjeang, E. In-situ simulation of membrane fatigue in polymer electrolyte fuel cells. Int. J. Hydrogen Energy 2017, 42, 11838–11844. [Google Scholar] [CrossRef]
- Chandesris, M.; Vincent, R.; Guetaz, L.; Roch, J.-S.; Thoby, D.; Quinaud, M. Membrane degradation in PEM fuel cells: From experimental results to semi-empirical degradation laws. Int. J. Hydrogen Energy 2017, 42, 8139–8149. [Google Scholar] [CrossRef]
- Shah, A.A.; Ralph, T.R.; Walsh, F.C. Modeling and Simulation of the Degradation of Perfluorinated Ion-Exchange Membranes in PEM Fuel Cells. J. Electrochem. Soc. 2009, 156, B465–B484. [Google Scholar] [CrossRef] [Green Version]
- Gummalla, M.; Atrazhev, V.V.; Condit, D.; Cipollini, N.; Madden, T.; Kuzminyh, N.Y.; Weiss, D.; Burlatsky, S.F. Degradation of Polymer-Electrolyte Membranes in Fuel Cells II. Theoretical model. J. Electrochem. Soc. 2010, 157, B1542–B1548. [Google Scholar] [CrossRef]
- Coulon, R.; Bessler, W.G.; Franco, A.A. Modeling Chemical Degradation of a Polymer Electrolyte Membrane and its Impact on Fuel Cell Performance. ECS Trans. 2010, 25, 259–273. [Google Scholar] [CrossRef]
- Singh, R.; Sui, P.C.; Wong, K.H.; Kjeang, E.; Knights, S.; Djilali, N. Modeling the Effect of Chemical Membrane Degradation on PEMFC Performance. J. Electrochem. Soc. 2018, 165, F3328–F3336. [Google Scholar] [CrossRef] [Green Version]
- Fink, C.; Gößling, S.; Karpenko-Jereb, L.; Urthaler, P. CFD Simulation of an Industrial PEM Fuel Cell with Local Degradation Effects. Fuel Cells 2020, 20, 431–452. [Google Scholar] [CrossRef]
- Quiroga, M.A.; Malek, K.; Franco, A.A. A Multiparadigm Modeling Investigation of Membrane Chemical Degradation in PEM Fuel Cells. J. Electrochem. Soc. 2016, 163, F59–F70. [Google Scholar] [CrossRef] [Green Version]
- Carcadea, E.; Varlam, M.; Marinoiu, A.; Raceanu, M.; Ismail, M.S.; Ingham, D.B. Influence of catalyst structure on PEM fuel cell performance—A numerical investigation. Int. J. Hydrogen Energy 2019, 44, 12829–12841. [Google Scholar] [CrossRef] [Green Version]
- Penga, Z.; Bergbreiter, C.; Barbir, F.; Scholta, J. Numerical and experimental analysis of liquid water distribution in PEM fuel cells. Energy Convers. Manag. 2019, 189, 167–183. [Google Scholar] [CrossRef]
- Rizvandi, O.B.; Yesilyurt, S. A pseudo three-dimensional, two-phase, non-isothermal model of proton exchange membrane fuel cell. Electrochim. Acta 2019, 302, 180–197. [Google Scholar] [CrossRef]
- Wang, Y.L.; Wang, S.X.; Liu, S.C.; Li, H.; Zhu, K. Three-dimensional simulation of a PEM fuel cell with experimentally measured through-plane gas effective diffusivity considering Knudsen diffusion and the liquid water effect in porous electrodes. Electrochim. Acta 2019, 318, 770–782. [Google Scholar] [CrossRef]
- Zhang, G.B.; Xie, X.; Xie, B.A.; Du, Q.; Jiao, K. Large-scale multi-phase simulation of proton exchange membrane fuel cell. Int. J. Heat Mass Transf. 2019, 130, 555–563. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.G. Oxygen transport in polymer electrolyte membrane fuel cells based on measured electrode pore structure and mass transport properties. Energy Convers. Manag. 2019, 186, 570–585. [Google Scholar] [CrossRef]










| Coefficient | Value |
|---|---|
| a0 | −2.1794 |
| a1 | +0.02953 K−1 |
| a2 | −9.1837 × 10−5 K−2 |
| a3 | +1.4454 × 10−7 K−3 |
| Coefficient | Value |
|---|---|
| b−1 | −5.8002206 × 103 |
| b0 | 1.3914993 |
| b1 | −0.048640239 |
| b2 | 4.1764768 × 10−5 |
| b3 | 1.4452093 × 10−8 |
| be | 6.5459673 |
| Coefficient | Value |
|---|---|
| K1 | 100 |
| K2 | 0.217 |
| E00 | −0.0417 kg mol−1 |
| E+0 | −0.052 kg mol−1 |
| E++ | −3.7216 kg mol−1 |
| Coefficient | Value |
|---|---|
| λmin | 1.65 |
| D+0 | 6.5 × 10−9 m2 s−1 |
| s | 0.83 |
| q | 1.5 |
| A+ | 0.084 |
| A0 | 0.5 |
| θdiff | 1800 K |
| Data Source | κ0/S m−1 | λ0 | θcond/K | ncond |
|---|---|---|---|---|
| Springer [39] | 0.5139 | 0.6344 | 1268 | 1 |
| van Bussel–Kulikovsky [57,87] | 0.5736 | 1.253 | undefined | 1 |
| Weber [65] | 0.2646 | 2 | 1800 | 1.5 |
| Wiezell [88], fit to Zawodzinski [52] | 0.45 | 0.222 | undefined | 1 |
| Meier [58], fit to Zawodzinski [79] | 0.491 * | 0.543 | 1190 | 1 |
| i | ai | bi |
|---|---|---|
| 0 | −0.8 | −0.1254 |
| 1 | 0.075 | 0.1832 |
| 2 | −6.375 × 10−4 | −8.65 × 10−3 |
| 3 | 1.93 × 10−5 | 9.4 × 10−5 |
| Data Source | λcrit | αξ,λ |
|---|---|---|
| Zawodzinski et al. [80] (room temperature) | 14 | 0.1875 |
| van Bussel–Kulikovsky (T = 80 °C) [57,87] | 9 | 0.117 |
| Data Source | ξ0 | αξ,T/K−1 |
|---|---|---|
| Ge et al. [109] | 1.984 | 0.0126 |
| Ise et al. [111] | 1.812 | 0.014 |
| Coefficient | H2 | O2 |
|---|---|---|
| ψV0/mol m−1 s−1 Pa−1 | 2.9 × 10−15 | 1.1 × 10−15 |
| ψw/mol m−1 s−1 Pa−1 | 2.2 × 10−14 | 1.9 × 10−14 |
| ψL0/mol m−1 s−1 Pa−1 | 1.8 × 10−14 | 1.2 × 10−14 |
| EA,DV/kJ mol−1 | 21 | 22 |
| EA,DL/kJ mol−1 | 18 | 20 |
| KH,gas,0/Pa m3 mol−1 | θsoln,gas/K | |
|---|---|---|
| H2 | 2.584 × 103 | −170 |
| O2 | 1.348 × 105 | 666 |
| HF | 4.149 × 108 | 7400 |
| H2O2 | 6.83 × 107 | 7379 |
| Gas | Dgas,0/m2 s−1 | θdiff,gas/K |
|---|---|---|
| H2 | 4.1× 10−7 | 2602 |
| O2 | 3.1 × 10−7 | 2736 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dickinson, E.J.F.; Smith, G. Modelling the Proton-Conductive Membrane in Practical Polymer Electrolyte Membrane Fuel Cell (PEMFC) Simulation: A Review. Membranes 2020, 10, 310. https://doi.org/10.3390/membranes10110310
Dickinson EJF, Smith G. Modelling the Proton-Conductive Membrane in Practical Polymer Electrolyte Membrane Fuel Cell (PEMFC) Simulation: A Review. Membranes. 2020; 10(11):310. https://doi.org/10.3390/membranes10110310
Chicago/Turabian StyleDickinson, Edmund J. F., and Graham Smith. 2020. "Modelling the Proton-Conductive Membrane in Practical Polymer Electrolyte Membrane Fuel Cell (PEMFC) Simulation: A Review" Membranes 10, no. 11: 310. https://doi.org/10.3390/membranes10110310
APA StyleDickinson, E. J. F., & Smith, G. (2020). Modelling the Proton-Conductive Membrane in Practical Polymer Electrolyte Membrane Fuel Cell (PEMFC) Simulation: A Review. Membranes, 10(11), 310. https://doi.org/10.3390/membranes10110310