Oxygen Transport Membranes for Efficient Glass Melting
Abstract
:1. Introduction
2. Review of Oxygen Transport Membranes
- A new 1-D OTM model is developed to predict the thermodynamic performance and design of planar membrane modules;
- The OTM model is calibrated using newly published experimental data from a 30 μm thick dense LSCF membrane;
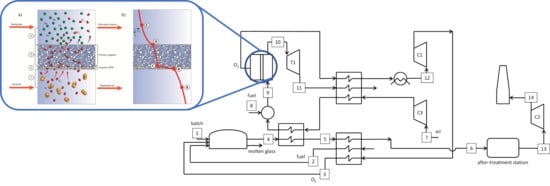
- The designed OTM modules are integrated into three new glass furnace layouts with oxy-fuel combustion;
- The proposed layouts are assessed from an energy and economic viewpoint to select the optimal configuration.
3. Modelling of Supported OTM
3.1. OTM Module Model
- One-dimensional analysis: numerical discretization in finite volumes along the axial directory of the streams. In each finite volume, the permeation model, the fluid-dynamic models are solved
- Steady state analysis
- Ideal gases and ideal mixtures
- Uniform distribution across all channels
- Negligible thermal losses towards the environment
3.2. Fluid-Dynamic and Heat Transfer Model
3.3. Permeation Model
- Gas phase diffusion of molecular oxygen from the bulk phase to the membrane surface on the feed side.
- Diffusion across the ceramic membrane layer; this comprises of the following sub-processes:
- Oxygen reduction (ORR), which involves: (i) surface exchange reaction on the feed side—chemisorption of the oxygen molecule onto a metal oxide at an oxide-ion vacancy; (ii) dissociation and reduction of O2 with the consequent production of oxygen anions; (iii) incorporation of O2− ion into the lattice structure [24].
- Ionic transport throughout the dense membrane material—single-phase (MIEC) or composite. Simultaneous bulk-diffusion of charged species and small polarons in the bulk phase.
- Surface-exchange reaction on the permeate interface—oxygen anions recombination to form molecular oxygen and oxygen vacancies in the solid structure
- Oxygen transport in the porous support structure.
- Gas diffusion and counter-diffusion of chemical species from the gas bulk to the membrane surface and vice-versa.
3.3.1. Gas Phase Bulk Diffusion
3.3.2. Solid Phase Bulk Diffusion
3.3.3. Superficial Reactions
3.3.4. Permeation in Porous Media
4. Calibration of Permeation Model
4.1. Experimental Set-Up
4.2. Results of Experimental Tests
- ▪
- air feed (200 NL min−1) and helium as sweep gas (100–300 NL min−1),
- ▪
- oxygen feed (200 NL min−1) and helium as sweep gas (100–300 NL min−1),
- ▪
- oxygen feed (200 NL min−1) and nitrogen as sweep gas (100–300 NL min−1).
4.3. Support Calibration
- J [m3 s−1 m−2] is the volumetric flux across the porous structure.
- t [m] is the support thickness.
- μ [Pa s] is the dynamic viscosity.
- α [m2] is a viscosity coefficient which represents the Δp losses due to diffusivity effects. This is a calibration parameter.
- ρ [kg m−3] is the average density.
- β [m] is a momentum coefficient which represents the Δp losses due to turbulent effects. This is a calibration parameter.
4.4. Supported Membrane Calibration
5. Heat and Mass Balance of Glass Melting Furnace
5.1. Air-Blown Reference Case
5.2. Oxyfuel Case with VSA Unit
5.3. Oxyfuel Cases with Integrated OTM Systems
5.4. Energy Assessment
5.5. Design and Performance of the Integrated OTMs
6. Economic Assessment
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| Channel width/ | |
| Channel height/ | |
| Volumetric molar concentration/ | |
| Concentration of mobile charge carriers k/ | |
| Binary diffusion coefficient of species i into k/ | |
| Hydraulic diameter/ | |
| Knudsen diffusion coefficient/ | |
| Activation energy of forward reaction/ | |
| Activation energy of reverse reaction/ | |
| Faraday constant/ | |
| Specific molar enthalpy/ | |
| Mass transfer coefficient/ | |
| Current density of charge carrier k/ | |
| Diffusive molar flux of species i/ | |
| Forward reaction rate constant/ | |
| Reverse reaction rate constant/ | |
| Equilibrium constant of reaction/- | |
| Molecular mass of species i/ | |
| Absolute molar flux of species i/ | |
| Pressure/ | |
| Thermal power/ | |
| Universal gas constant/ | |
| Average pore radius/ | |
| Reaction rate/ | |
| Sherwood number/- | |
| Temperature/ | |
| Support thickness/ | |
| Molar fraction of species i/- | |
| Velocity/ | |
| Number of charge carrier k/- | |
| Transversal coordinate through supported membrane/- | |
| Greek symbols | |
| Mass diffusion boundary layer/ | |
| Standard reaction enthalpy/ | |
| Average porosity/- | |
| Electrostatic potential/ | |
| Chemical potential of charge carrier k/ | |
| Molecule diffusion volume of species i/- | |
| Charge carrier k conductivity/ | |
| Average tortuosity/- | |
| Acronyms | |
| OTM | Oxygen Transport Membrane |
| MIEC | Mixed Ionic-Electronic Conductor |
| ORR | Oxygen Reduction Reaction |
| TPB | Triple Phase Boundary |
| DPB | Double Phase Boundary |
| SFM | Stagnant Film Model |
| DGM | Dusty Gas Model |
| SOFC | Solid Oxide Fuel Cells |
| VSA | Vacuum Swing Adsorption |
| PSA | Pressure Swing Adsorption |
| Subscripts/Superscripts | |
| Membrane wall | |
| Gas bulk phase | |
| Mixture | |
| ′ | Feed (reduction) side |
| ″ | Permeate (oxidation) side |
| Effective property | |
| Knudsen diffusion term | |
Appendix A
| Stream | ṁ, kg h−1 | T, °C | p, kPa | Ar | CO2 | H2O | N2 | O2 |
|---|---|---|---|---|---|---|---|---|
| 1 | 3750.0 | 15.0 | ||||||
| 2 | 309.3 | 15.0 | fuel (CH4: 89, C2H6: 7, CO2: 2, C3H8: 1.11; N2: 0.89) | |||||
| 3 | 5559.8 | 15.0 | 101 | 0.92 | 0.03 | 1.03 | 77.28 | 20.73 |
| 4 | 5559.8 | 21.4 | 107 | 0.92 | 0.03 | 1.03 | 77.28 | 20.73 |
| 5 | 5559.8 | 935.2 | 0.92 | 0.03 | 1.03 | 77.28 | 20.73 | |
| 6 | 5869.1 | 1313.7 | 0.84 | 8.86 | 17.54 | 70.76 | 2 | |
| 7 | 8732.9 | 361.8 | 0.87 | 6.03 | 12.25 | 72.85 | 8 | |
| 8 | 24828.1 | 46.6 | 93 | 0.84 | 2.12 | 11.20 | 70.86 | 14.98 |
| 9 | 24828.1 | 58.1 | 102 | 0.84 | 2.12 | 11.20 | 70.86 | 14.98 |
| Stream | ṁ, kg h−1 | T, °C | p, kPa | Ar | CO2 | H2O | N2 | O2 |
|---|---|---|---|---|---|---|---|---|
| 1 | 3750.0 | |||||||
| 2 | 235.7 | 450 | fuel (CH4: 89, C2H6: 7, CO2: 2, C3H8: 1.11; N2: 0.89) | |||||
| 3 | 983.2 | 15.0 | 101 | 4.00 | 4.00 | 92.00 | ||
| 4 | 983.2 | 21.5 | 107 | 4.00 | 4.00 | 92.00 | ||
| 5 | 983.2 | 550.0 | 104 | 4.00 | 4.00 | 92.00 | ||
| 6 | 1219.0 | 1313.7 | 101 | 2.76 | 32.04 | 60.17 | 3.03 | 2.00 |
| 7 | 1219.0 | 835.3 | 2.76 | 32.04 | 60.17 | 3.03 | 2.00 | |
| 8 | 10804.0 | 50.9 | 93 | 1.08 | 3.71 | 13.88 | 64.03 | 17.31 |
| 9 | 10804.0 | 62.4 | 102 | 1.08 | 3.71 | 13.88 | 64.03 | 17.31 |
| 10 | 1306.4 | 15.0 | 101 | 0.92 | 0.03 | 1.03 | 77.28 | 20.73 |
| 11 | 1306.4 | 25.6 | 111 | 0.92 | 0.03 | 1.03 | 77.28 | 20.73 |
| 12 | 1306.4 | 750 | 0.92 | 0.03 | 1.03 | 77.28 | 20.73 | |
| Stream | ṁ, kg/h | T, °C | p, kPa | Ar | CO2 | H2O | N2 | O2 |
|---|---|---|---|---|---|---|---|---|
| 1 | 3750 | |||||||
| 2 | 234.4 | 450.0 | fuel (CH4: 89, C2H6: 7, CO2: 2, C3H8: 1.11; N2: 0.89) | |||||
| 3 | 893.6 | 550.0 | 107 | 100.00 | ||||
| 4 | 1128.0 | 1313.7 | 101 | 33.96 | 63.77 | 0.28 | 2.00 | |
| 5 | 1128.0 | 800.0 | 101 | 33.96 | 63.77 | 0.28 | 2.00 | |
| 6 | 1128.0 | 501.0 | 101 | 33.96 | 63.77 | 0.28 | 2.00 | |
| 7 | 8690.4 | 15.0 | 101 | 0.92 | 0.03 | 1.03 | 77.28 | 20.73 |
| 8 | 57.1 | 15.0 | fuel (CH4: 89, C2H6: 7, CO2: 2, C3H8: 1.11; N2: 0.89) | |||||
| 9 | 8747.6 | 950.0 | 400 | 0.91 | 1.16 | 3.14 | 76.45 | 18.34 |
| 10 | 7853.8 | 950.0 | 400 | 1.00 | 1.28 | 3.46 | 84.17 | 10.10 |
| 11 | 7853.8 | 648.0 | 103 | 1.00 | 1.28 | 3.46 | 84.17 | 10.10 |
| 12 | 893.6 | 40.0 | 24 | 100.00 | ||||
| 13 | 5583.6 | 58.3 | 93 | 0.68 | 7.06 | 19.76 | 56.85 | 15.65 |
| 14 | 5583.6 | 69.8 | 102 | 0.68 | 7.06 | 19.76 | 56.85 | 15.65 |
| Stream | ṁ, kg h−1 | T, °C | p, kPa | Ar | CO2 | H2O | N2 | O2 |
|---|---|---|---|---|---|---|---|---|
| 1 | 3750.0 | |||||||
| 2 | 260.8 | 15.0 | fuel (CH4: 89, C2H6: 7, CO2: 2, C3H8: 1.11; N2: 0.89) | |||||
| 3 | 2280.8 | 950.0 | 0.04 | 40.64 | 5.46 | 3.86 | 50.00 | |
| 4 | 2541.5 | 1313.7 | 0.03 | 52.78 | 41.91 | 3.28 | 2.00 | |
| 5 | 2541.5 | 900.0 | 0.03 | 52.78 | 41.91 | 3.28 | 2.00 | |
| 6 | 2541.5 | 250.0 | 0.03 | 52.78 | 41.91 | 3.28 | 2.00 | |
| 7 | 2019.1 | 40.0 | 93 | 0.05 | 83.65 | 7.93 | 5.2 | 3.17 |
| 8 | 2019.1 | 49.0 | 102 | 0.05 | 83.65 | 7.93 | 5.2 | 3.17 |
| 9 | 32.7 | 15.0 | 101 | 0.92 | 0.03 | 1.03 | 77.28 | 20.73 |
| 10 | 1260.3 | 61.7 | 111 | 0.09 | 80.62 | 7.68 | 7.81 | 3.81 |
| 11 | 1260.3 | 700.0 | 109 | 0.09 | 80.62 | 7.68 | 7.81 | 3.81 |
| 12 | 9.4 | 15.0 | fuel (CH4: 89, C2H6: 7, CO2: 2, C3H8: 1.11; N2: 0.89) | |||||
| 13 | 1269.7 | 950.0 | 107 | 0.08 | 81.01 | 10.87 | 7.69 | 0.34 |
| 14 | 9862.2 | 192.1 | 434 | 0.92 | 0.03 | 1.03 | 77.28 | 20.73 |
| 15 | 9862.2 | 330.8 | 425 | 0.92 | 0.03 | 1.03 | 77.28 | 20.73 |
| 16 | 9862.2 | 550.0 | 416 | 0.92 | 0.03 | 1.03 | 77.28 | 20.73 |
| 17 | 9862.2 | 700.0 | 408 | 0.92 | 0.03 | 1.03 | 77.28 | 20.73 |
| 18 | 66.4 | 15.0 | fuel (CH4: 89, C2H6: 7, CO2: 2, C3H8: 1.11; N2: 0.89) | |||||
| 19 | 9928.8 | 950.0 | 400 | 0.91 | 1.19 | 3.19 | 76.43 | 18.28 |
| 20 | 8917.6 | 950.0 | 400 | 1.00 | 1.31 | 3.52 | 84.12 | 10.06 |
| 21 | 8917.6 | 648.1 | 103 | 1.00 | 1.31 | 3.52 | 84.12 | 10.06 |
| 22 | 8917.6 | 415.5 | 101 | 1.00 | 1.31 | 3.52 | 84.12 | 10.06 |
- a pressure ratio of 1.06 for the blower C1 (air to the burners);
- a pressure ratio of 1.1 for the blower C2 (extraction of the gas from the after-treatment station).
- a pressure ratio of 1.06 for the blower C1 (oxygen to pre-heater then to burners);
- a pressure ratio of 1.1 for the blower C2 (extraction of the gas from the after-treatment station);
- a pressure ratio of 1.1 for the blower C3 (delivering the hot carrier through the regenerative heat exchanger for oxygen and fuel pre-heating);
- pressure ratios of 4.43 and 1.1 for the vacuum pump C1 and the blower C2, respectively, with the previously considered efficiency values;
- a pressure ratio of 4.2 with an isentropic efficiency of 83% for the compressor C3;
- a pressure ratio of 3.88 with an isentropic efficiency of 87% for the turbine T1;
- a mechanical-electrical efficiency of 0.9 for the micro-gas turbine including the compressor C3 and the turbine T1.
- pressure ratios of 1.1 for both the blowers C1 and C2, with the previously considered efficiency values;
- a pressure ratio of 4.28 (differently from the case in Figure 13, one more passage through heat exchanger is considered here) with an isentropic efficiency of 83% for the compressor C3;
- a pressure ratio of 3.88 with an isentropic efficiency of 87% for the turbine T1;
- a mechanical-electrical efficiency of 0.9 for the micro-gas turbine including the compressor C3 and the turbine T1.
References
- Vellini, M.; Savioli, M. Energy and environmental analysis of glass container production and recycling. Energy 2009, 34, 2137–2143. [Google Scholar] [CrossRef]
- Schmitz, A.; Kamiński, J.; Scalet, B.M.; Soria, A. Energy consumption and CO2 emissions of the European glass industry. Energy Policy 2011, 39, 142–155. [Google Scholar] [CrossRef]
- El-Behery, S.M.; Hussien, A.; Kotb, H.; El-Shafie, M. Performance evaluation of industrial glass furnace regenerator. Energy 2017, 119, 1119–1130. [Google Scholar] [CrossRef]
- Sardeshpande, V.R.; Anthony, R.; Gaitonde, U.; Banerjee, R. Performance analysis for glass furnace regenerator. Appl. Energy 2011, 88, 4451–4458. [Google Scholar] [CrossRef]
- Sardeshpande, V.; Gaitonde, U.; Banerjee, R. Model based energy benchmarking for glass furnace. Energy Convers. Manag. 2007, 48, 2718–2738. [Google Scholar] [CrossRef]
- Beerkens, R.G.C. New concepts for energy efficient & emission friendly melting of glass. Ceramic Trans. Ser. 2012, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Beerkens, R.G.C.; Van Limpt, J. Energy efficiency benchmarking of glass furnaces. Ceramic Eng. Sci. Proceed. 2008, 93–105. [Google Scholar] [CrossRef]
- Beerkens, R.G.C. Energy balances of glass furnaces: Parameters determining energy consumption of glass melt processes. In Mechanical Properties and Performance of Engineering Ceramics and Composites VI 2007; John Wiley & Sons: New York, NY, USA, 2009; pp. 102–116. [Google Scholar]
- Dyer, P. Ion transport membrane technology for oxygen separation and syngas production. Solid State Ion. 2000, 134, 21–33. [Google Scholar] [CrossRef]
- Sunarso, J.; Baumann, S.; Serra, J.M.; Meulenberg, W.A.; Liu, S.; Lin, Y.S.; Da Costa, J.C.D. Mixed ionic-electronic conducting (MIEC) ceramic-based membranes for oxygen separation. J. Membr. Sci. 2008, 320, 13–41. [Google Scholar] [CrossRef]
- Brown, J. Solid oxide fuel cell technology. IEEE Trans. Energy Convers. 1988, 3, 193–198. [Google Scholar] [CrossRef]
- Serra, J.M.; Garcia-Fayos, J.; Baumann, S.; Schulze-Küppers, F.; Meulenberg, W.A. Oxygen permeation through tape-cast asymmetric all-La0.6Sr0.4Co0.2Fe0.8O3−δ membranes. J. Membr. Sci. 2013, 447, 297–305. [Google Scholar] [CrossRef]
- Plazaola, A.A.; Cruellas, A.; Liu, Y.; Porras, N.B.; Tanaka, D.A.P.; Annaland, M.V.S.; Gallucci, F. Mixed ionic-electronic conducting membranes (MIEC) for their application in membrane reactors: A review. Processes 2019, 7, 128. [Google Scholar] [CrossRef] [Green Version]
- Kishimoto, M.; Lomberg, M.; Ruiz-Trejo, E.; Brandon, N.P. Towards the design-led optimization of solid oxide fuel cell electrodes. ECS Trans. 2015, 68, 2019–2028. [Google Scholar] [CrossRef]
- Chen, C. Microstructural development, electrical properties and oxygen permeation of zirconia-palladium composites. Solid State Ion. 1995, 76, 23–28. [Google Scholar] [CrossRef] [Green Version]
- Zou, Y.; Schulze-Küppers, F.; Balaguer, M.; Malzbender, J.; Krüger, M. Creep behavior of porous La0.6Sr0.4Co0.2Fe0.8O3-δ substrate material for oxygen separation application. J. Eur. Ceram. Soc. 2018, 38, 1702–1710. [Google Scholar] [CrossRef]
- Kirchen, P.; Apo, D.J.; Hunt, A.; Ghoniem, A.F. A novel ion transport membrane reactor for fundamental investigations of oxygen permeation and oxy-combustion under reactive flow conditions. Proc. Combust. Inst. 2013, 34, 3463–3470. [Google Scholar] [CrossRef]
- Habib, M.A.; Nemitallah, M.; Ben-Mansour, R.; Ben-Mansour, R. Recent development in oxy-combustion technology and its applications to gas turbine combustors and ITM reactors. Energy Fuels 2012, 27, 2–19. [Google Scholar] [CrossRef]
- Mancini, N.; Mitsos, A. Ion transport membrane reactors for oxy-combustion–Part II: Analysis and comparison of alternatives. Energy 2011, 36, 4721–4739. [Google Scholar] [CrossRef]
- Allam, R.J. Improved oxygen production technologies. Energy Procedia 2009, 1, 461–470. [Google Scholar] [CrossRef] [Green Version]
- Geffroy, P.-M.; Vivet, A.; Guironnet, L.; Richet, N.; Rossignol, F.; Chartier, T. Perovskite foams used in combination with dense ceramic membranes for oxygen transport membrane applications. Ceram. Int. 2018, 44, 19831–19835. [Google Scholar] [CrossRef]
- Giostri, A.; Di Marcoberardino, G.; Chiesa, P.; Campanari, S. Simulation of oxygen transport membranes for CPO reactors in small-scale hydrogen or Syngas production applications. Energy Procedia 2017, 142, 1589–1594. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Adler, S.B.; Lane, J.A.; Steele, B.C.H. Electrode kinetics of porous mixed-conducting oxygen electrodes. J. Electrochem. Soc. 1996, 143, 3554–3564. [Google Scholar] [CrossRef]
- Mancini, N.; Mitsos, A. Ion transport membrane reactors for oxy-combustion – Part I: Intermediate-fidelity modeling. Energy 2011, 36, 4701–4720. [Google Scholar] [CrossRef]
- Zydney, A.L. Stagnant film model for concentration polarization in membrane systems. J. Membr. Sci. 1997, 130, 275–281. [Google Scholar] [CrossRef]
- Brouwers, H.; Chesters, A. Film models for transport phenomena with fog formation: The classical film model. Int. J. Heat Mass Transf. 1992, 35, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Brouwers, H.J.H. Stagnant film model for effect of diffusional layer thickness on heat transfer and exerted friction. AIChE J. 1995, 41, 1821–1825. [Google Scholar] [CrossRef] [Green Version]
- Poling, B.E.; Prausnitz, J.M.; O’Connel, J.P. Properties of Gases and Liquids, 5th ed.; The McGraw-Hill Companies: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Krishna, R.; Wesselingh, J. The Maxwell-Stefan approach to mass transfer. Chem. Eng. Sci. 1997, 52, 861–911. [Google Scholar] [CrossRef]
- Xu, S.J.; Thomson, W.J. Oxygen permeation rates through ion-conducting perovskite membranes. Chem. Eng. Sci. 1999, 54, 3839–3850. [Google Scholar] [CrossRef]
- Hunt, A.; Dimitrakopoulos, G.; Kirchen, P.; Ghoniem, A.F. Measuring the oxygen profile and permeation flux across an ion transport (La0.9Ca0.1FeO3−δ) membrane and the development and validation of a multistep surface exchange model. J. Membr. Sci. 2014, 468, 62–72. [Google Scholar] [CrossRef]
- Chen, C.; Kruidhof, H.; Bouwmeester, H.J.M.; Verweij, H.; Burggraaf, A. Thickness dependence of oxygen permeation through erbiastabilized bismuth oxide-silver composites. Solid State Ion. 1997, 99, 215–219. [Google Scholar] [CrossRef] [Green Version]
- Bao, C.; Jiang, Z.; Zhang, X. Modeling mass transfer in solid oxide fuel cell anode: I. Comparison between Fickian, Stefan-Maxwell and dusty-gas models. J. Power Sources 2016, 310, 32–40. [Google Scholar] [CrossRef]
- Zhu, H.; Kee, R.J.; Janardhanan, V.M.; Deutschmann, O.; Goodwin, D.G. Modeling Elementary Heterogeneous Chemistry and Electrochemistry in Solid-Oxide Fuel Cells. J. Electrochem. Soc. 2005, 152, 2427–2440. [Google Scholar] [CrossRef] [Green Version]
- Baumann, S.; Schulze-Küppers, F.; Roitsch, S.; Betz, M.; Zwick, M.; Pfaff, E.; Meulenberg, W.A.; Mayer, J.; Stöver, D. Influence of sintering conditions on microstructure and oxygen permeation of Ba0.5Sr0.5Co0.8Fe0.2O3−δ (BSCF) oxygen transport membranes. J. Membr. Sci. 2010, 359, 102–109. [Google Scholar] [CrossRef]
- Drago, F.; Schulze-Küppers, S.; Baumann, P. Pinacci, Experimental and theoretical approach for evaluation of porous support resistance on the permeation of oxygen separation membranes. In Proceedings of the Euromembrane, Aachen, Germany, 8–10 September 2015. [Google Scholar]
- Drago, F.; Schulze-Küppers, S.; Baumann, P. Pinacci, Porous support resistance on the permeation of asymmetric LSCF membrane in the presence of sweep gas. In Proceedings of the 14th International Conference on Inorganic Membranes, Atlanta, GA, USA, 10–13 July 2016. [Google Scholar]
- Baumann, S.; Serra, J.M.; Lobera, M.; Escolástico, S.; Schulze-Küppers, F.; Meulenberg, W.A. Ultrahigh oxygen permeation flux through supported Ba0.5Sr0.5Co0.8Fe0.2O3−δ membranes. J. Membr. Sci. 2011, 377, 198–205. [Google Scholar] [CrossRef] [Green Version]
- Metals, G.S. GKN Sinter Metals: Product Catalogue for Metallic Membranes, (n.d.). Available online: https://docplayer.org/15696083-Metallische-membranen-sika-r-as-metal-membranes-sika-r-as.html (accessed on 17 December 2020).
- Kong, W.; Zhang, Q.; Xu, X.; Chen, D. A simple expression for the tortuosity of gas transport paths in solid oxide fuel cells’ porous electrodes. Energies 2015, 8, 13953–13959. [Google Scholar] [CrossRef] [Green Version]
- Joos, J.; Carraro, T.; Weber, A.; Ivers-Tiffée, E. Reconstruction of porous electrodes by FIB/SEM for detailed microstructure modeling. J. Power Sources 2011, 196, 7302–7307. [Google Scholar] [CrossRef]
- GS (Gas-Steam Cycles)—Department of Energy, Politecnico di Milano, (n.d.). Available online: http://www.gecos.polimi.it/expertise/software-development/ (accessed on 17 December 2020).
- Chiesa, P.; Macchi, E. A thermodynamic analysis of different options to break 60% electric efficiency in combined cycle power plants. J. Eng. Gas Turbines Power 2004, 126, 770–785. [Google Scholar] [CrossRef]
- Giuffrida, A.; Moioli, S.; Romano, M.C.; Lozza, G. Lignite-fired air-blown IGCC systems with pre-combustion CO2 capture. Int. J. Energy Res. 2016, 40, 831–845. [Google Scholar] [CrossRef]
- Bonalumi, D.; Giuffrida, A. Investigations of an air-blown integrated gasification combined cycle fired with high-sulphur coal with post-combustion carbon capture by aqueous ammonia. Energy 2016, 117, 439–449. [Google Scholar] [CrossRef]
- Cloete, S.; Giuffrida, A.; Romano, M.; Chiesa, P.; Pishahang, M.; Larring, Y. Integration of chemical looping oxygen production and chemical looping combustion in integrated gasification combined cycles. Fuel 2018, 220, 725–743. [Google Scholar] [CrossRef]
- Zaabout, A.; Romano, M.C.; Cloete, S.; Giuffrida, A.; Morud, J.; Chiesa, P.; Amini, S. Thermodynamic assessment of the swing adsorption reactor cluster (SARC) concept for post-combustion CO2 capture. Int. J. Greenh. Gas Control. 2017, 60, 74–92. [Google Scholar] [CrossRef]
- Beerkens, R.G.C.; Muysenberg, H.P. Comparative study on energy-saving technologies for glass furnaces. Glas. Berichte 1992, 65, 216–224. [Google Scholar]
- An Innovative Oxygen Combustion Technology for Environment Friendly Primary Flat Glass Production, (n.d.). Available online: https://www.oxyfuel-heatrecovery.com/project/welcome-hotoxyglass-life-project (accessed on 24 January 2018).
- Bermudez, J.M.; Garcia-Fayos, J.; Reina, T.R.; Reed, G.; Persoon, E.S.; Görtz, D.; Schroeder, M.; Millan, M.; Serra, J.M. Thermochemical stability of LaxSr1-xCoyFe1-yO3-δ and NiFe2O4-Ce0.8Tb0.2O2-δ under real conditions for its application in oxygen transport membranes for oxyfuel combustion. J. Membr. Sci. 2018, 562, 26–37. [Google Scholar] [CrossRef]
- Galanti, L.; Massardo, A.F. Micro gas turbine thermodynamic and economic analysis up to 500kWe size. Appl. Energy 2011, 88, 4795–4802. [Google Scholar] [CrossRef]
- Final Publishable Report Summary—DEMOYS. 2015. Available online: https://cordis.europa.eu/docs/results/241/241309/final1-demoys-publishable-summary-report-re1.pdf (accessed on 17 December 2020).















| A | B | C | D | |
|---|---|---|---|---|
| Fuel energy introduced in the furnace, kWth | 3992.7 | 3043.5 | 3026.6 | 3368.4 |
| Heat carried in the glass, kWth | 1628.1 | 1628.1 | 1628.1 | 1628.1 |
| Heat recovered and recycled into the furnace, kWth | 1542.7 | 218 | 153.6 | 251.5 |
| Heat supply from O2 separation, kWth | - | - | 55.4 | 271.4 |
| Heat introduced by supplementary fuel, kWth | - | - | - | 121.0 |
| Heat loss in the flue gas, kWth | 910.4 | 475.2 | 217.3 | 194.0 |
| Other heat losses, kWth | 1464.6 | 945.9 | 945.9 | 1091.7 |
| Heat transferred to the micro-gas turbine cycle, kWth | - | - | 290.9 | 860.4 |
| A | B | C | D | |
|---|---|---|---|---|
| Fuel to the glass melting furnace, kWth | 3992.7 | 3043.5 | 3043.5 | 3368.4 |
| Electric power duty due to auxiliaries, kWel | 105.1 | 47.3 | 77.1 | 8.4 |
| Electric power duty for O2 production, kWel | - | 275.2 | - | |
| Electric power from the micro-gas turbine, kWel | - | - | −319.6 | −374.2 |
| Overall electric power, kWel | 105.1 | 322.5 | −242.5 | −365.8 |
| Equivalent fuel, kg/h | 16.3 | 50.0 | −37.6 | −56.7 |
| Additional fuel, kg/h | - | - | 57.1 | 75.8 |
| Primary fuel, kWth | 4202.9 | 3688.5 | 3280 | 3616 |
| No Sweep (3-end) OTM | Sweep (4-end) OTM | ||||
|---|---|---|---|---|---|
| Split fraction | % | 40% | 50% | 60% | 50% |
| O2 Molar flow rate | mol s−1 | 7.76 | 8.80 | ||
| channel width | mm | 21.5 | 21.5 | 21.5 | 21.5 |
| wall thick | mm | 2.5 | 2.5 | 2.5 | 2.5 |
| channel per layer | - | 20 | 20 | 20 | 20 |
| membrane width | m | 0.480 | 0.480 | 0.480 | 0.480 |
| layers per stack | - | 50 | 50 | 50 | 50 |
| b/afeed | - | 1.00 | 1.00 | 1.00 | 1.00 |
| b/aperm | - | 3.01 | 3.01 | 3.01 | 3.01 |
| membrane thickness | μm | 30.00 | 30.00 | 30.00 | 30.00 |
| support thickness | mm | 0.70 | 0.70 | 0.70 | 0.70 |
| membrane height | m | 0.032 | 0.032 | 0.032 | 0.032 |
| membrane per stack | - | 50 | 50 | 50 | 50 |
| stack height | m | 1.590 | 1.590 | 1.590 | 1.590 |
| channel length | m | 0.480 | 0.480 | 0.480 | 0.480 |
| membrane area | m2 | 0.23 | 0.23 | 0.23 | 0.23 |
| channels number | - | 42538 | 47087 | 54795 | 97083 |
| Active area | m2 | 438 | 484 | 568 | 1003 |
| O2 Volume Flux | NmL cm−2 min−1 | 2.598 | 2.352 | 2.001 | 1.180 |
| Pressure loss feed | mbar | 0.002 | 0.001 | 0.001 | 0.750 |
| Pressure loss permeate | mbar | - | - | - | 0.86 |
| stack area | m2 | 11.6 | 11.6 | 11.6 | 11.5 |
| stack volume | m3 | 0.37 | 0.37 | 0.37 | 0.37 |
| stack number | - | 38 | 42 | 49 | 87 |
| B | C | |
|---|---|---|
| Cost of plant *, k€ | 2378.7 | 2482.1 |
| Yearly cost of fuel for the furnace, k€ | 1849.4 | 1839.4 |
| Yearly cost of additional fuel, k€ | - | 448.3 |
| Yearly cost of electricity, k€ | 410.2 | −308.5 |
| Discounted total cost, M€ | 17.54 | 15.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mastropasqua, L.; Drago, F.; Chiesa, P.; Giuffrida, A. Oxygen Transport Membranes for Efficient Glass Melting. Membranes 2020, 10, 442. https://doi.org/10.3390/membranes10120442
Mastropasqua L, Drago F, Chiesa P, Giuffrida A. Oxygen Transport Membranes for Efficient Glass Melting. Membranes. 2020; 10(12):442. https://doi.org/10.3390/membranes10120442
Chicago/Turabian StyleMastropasqua, Luca, Francesca Drago, Paolo Chiesa, and Antonio Giuffrida. 2020. "Oxygen Transport Membranes for Efficient Glass Melting" Membranes 10, no. 12: 442. https://doi.org/10.3390/membranes10120442
APA StyleMastropasqua, L., Drago, F., Chiesa, P., & Giuffrida, A. (2020). Oxygen Transport Membranes for Efficient Glass Melting. Membranes, 10(12), 442. https://doi.org/10.3390/membranes10120442