Experimental Design as a Tool for Optimizing and Predicting the Nanofiltration Performance by Treating Antibiotic-Containing Wastewater
Abstract
:1. Introduction
2. Theory
3. Materials and Methods
4. Results and Discussion
4.1. Membrane Characterisation
4.2. Effect of Control Factors on Permeate Flux
4.3. Effect of Control Factors on Rejection
4.4. Modeling for Predictions of Permeate Flux and Antibiotic Rejection
4.5. External Model Validation
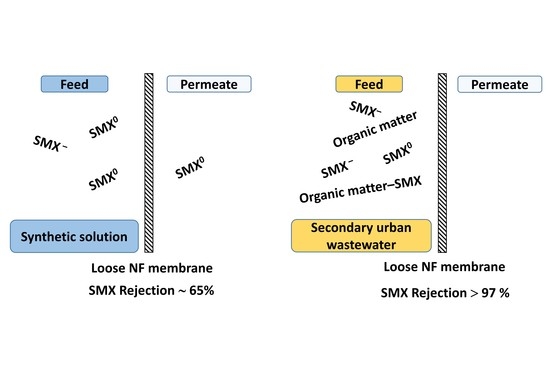
4.6. Effect of the Wastewater Background Matrix on the NF Performance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Klein, E.Y.; Van Boeckel, T.B.; Martinez, E.M.; Pant, S.; Gandra, S.; Levin, S.A.; Goossens, H.; Laxminarayan, R. Global increase and geographic convergence in antibiotic consumption between 2000 and 2015. PNAS 2018, 115, 3463–3470. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Senta, I.; Terzic, S.; Ahel, M. Occurrence and fate of dissolved and particulate antimicrobials in municipal wastewater treatment. Water Res. 2013, 47, 705–714. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, J.; Xu, Y.; Wang, H.; Guo, C.; Qiu, H.; He, Y.; Zhang, Y.; Li, X.; Meng, W. Occurrence of antibiotics and antibiotic resistance genes in a sewage treatment plant and its effluent-receiving river. Chemosphere 2015, 119, 1379–1385. [Google Scholar] [CrossRef]
- Baransi-Karkaby, K.; Bass, M.; Freger, V. In situ modification of reverse osmosis membrane elements for enhanced removal of multiple micropollutants. Membranes 2019, 9, 28. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gorito, A.M.; Ribeiro, A.R.; Almeida, C.M.R.; Silva, A.M.T. A review on the application of constructed wetlands for the removal of priority substances and contaminants of emerging concern listed in recently launched EU legislation. Environ. Pollut. 2017, 227, 428–443. [Google Scholar] [CrossRef] [PubMed]
- Shanmuganathan, S.; Loganathan, P.; Kazner, C.; Johir, M.A.H.; Vigneswaran, S. Submerged membrane filtration adsorption hybrid system for the removal of organic micropollutants from a water reclamation plant reverse osmosis concentrate. Desalination 2017, 401, 134–141. [Google Scholar] [CrossRef] [Green Version]
- Giacobbo, A.; Soares, E.V.; Bernardes, A.M.; Rosa, M.J.; de Pinho, M.N. Atenolol removal by nanofiltration: A case-specific mass transfer correlation. Water Sci. Technol. 2020, 81, 210–216. [Google Scholar] [CrossRef]
- Li, D.; Yan, M.; Hu, J.; Ren, L.; Zhang, Y.; Li, K. Determination and fate of oxytetracycline and related compounds in oxytetrac. Environ. Toxicol. 2008, 27, 80–86. [Google Scholar] [CrossRef]
- de Cazes, M.; Abejón, R.; Belleville, M.-P.; Sanchez-Marcano, J. Membrane bioprocesses for pharmaceutical micropollutant removal from waters. Membranes 2014, 4, 692–729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aziz, M.; Ojumu, T. Exclusion of estrogenic and androgenic steroid hormones from municipal membrane bioreactor wastewater using UF/NF/RO membranes for water reuse application. Membranes 2020, 10, 37. [Google Scholar] [CrossRef] [Green Version]
- Larsson, D.G.J. Pollution from drug manifacturing: Review and perspectives. Philos. Trans. R. Soc. B. 2014, 369, 20130571–20130578. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fick, J.; Söderström, H.; Lindberg, R.H.; Phan, C.; Tysklind, M.; Larsson, D.G.J. Contamination of surface, ground, and drinking water from pharmaceutical production. Environ. Toxicol. Chem. 2009, 28, 2522–2527. [Google Scholar] [CrossRef] [PubMed]
- Bisarya, S.C.; Patil, D.M. Determination of salicylic-acid and phenol (ppm level) in effluent from aspirin plant. Res. Ind. 1993, 38, 170–172. [Google Scholar]
- Wang, J.; Zhuan, R.; Chu, L. The occurrence, distribution and degradation of antibiotics by ionizing radiation: An overview. Sci. Total Environ. 2019, 646, 1385–1397. [Google Scholar] [CrossRef]
- Montagner, C.C.; Sodré, F.F.; Acayaba, R.D.; Vidal, C.; Campestrini, I.; Locatelli, M.A.; Pescara, I.C.; Albuquerque, A.F.; Umbuzeiro, G.A.; Jardim, W.F. Ten years-snapshot of the occurrence of emerging contaminants in drinking, surface and ground waters and wastewaters from São Paulo State, Brazil. J. Braz. Chem. Soc. 2019, 30, 614–632. [Google Scholar] [CrossRef]
- Rutgersson, C.; Fick, J.; Marathe, N.; Kristiansson, E.; Janzon, A.; Angelin, M.; Johansson, A.; Shouche, Y.; Flach, C.F.; Larsson, D.G.J. Fluoroquinolones and qnr genes in sediment, water, soil, and human fecal flora in an environment polluted by manufacturing discharges. Environ. Sci. Technol. 2014, 48, 7825–7832. [Google Scholar] [CrossRef]
- Shah, A.D.; Huang, C.; Kim, J. Mechanisms of antibiotic removal by nanofiltration membranes: Model development and application. J. Memb. Sci. 2012, 389, 234–244. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Zhang, T.; Li, X. Performance of nanofiltration membrane in rejecting trace organic compounds: Experiment and model prediction. Desalination 2015, 370, 7–16. [Google Scholar] [CrossRef]
- Kim, T.; Drewes, J.E.; Summers, R.S.; Amy, G.L. Solute transport model for trace organic neutral and charged compounds through nanofiltration and reverse osmosis membranes. Water Res. 2007, 41, 3977–3988. [Google Scholar] [CrossRef]
- Kong, F.; Wang, X.; Yang, H.; Chen, J.; Guo, C.; Zhang, T.; Xie, Y.F. The role of solubility on the rejection of trace organics by nanofiltration membrane: Exemplified with disinfection by-products. Environ. Sci. Pollut. Res. 2017, 24, 18400–18409. [Google Scholar] [CrossRef]
- Xu, R.; Zhou, M.; Wang, H.; Wang, X.; Wen, X. Influences of temperature on the retention of PPCPs by nanofiltration membranes: Experiments and modeling assessment. J. Memb. Sci. 2020, 599, 117817. [Google Scholar] [CrossRef]
- Yangali-Quintanilla, V.; Sadmani, A.; McConville, M.; Kennedy, M.; Amy, G. A QSAR model for predicting rejection of emerging contaminants pharmaceuticals, (endocrine disruptors) by nanofiltration membranes. Water Res. 2010, 44, 373–384. [Google Scholar] [CrossRef] [PubMed]
- Flyborg, L.; Björlenius, B.; Ullner, M.; Persson, K.M. A PLS model for predicting rejection of trace organic compounds by nanofiltration using treated wastewater as feed. Sep. Purif. Technol. 2017, 174, 212–221. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Comerton, A.M.; Andrews, R.C.; Bagley, D.M.; Hao, C. The rejection of endocrine disrupting and pharmaceutically active compounds by NF and RO membranes as a function of compound and water matrix properties. J. Memb. Sci. 2008, 313, 323–335. [Google Scholar] [CrossRef]
- Catarino, M.; Mendes, A. Dealcoholizing wine by membrane separation processes. Innov. Food Sci. Emerg. Technol. 2011, 12, 330–337. [Google Scholar] [CrossRef]
- Giacobbo, A.; Oliveira, M.; Duarte, E.C.N.F.; Mira, H.M.C.; Bernardes, A.M.; de Pinho, M.N. Ultrafiltration Based Process for the Recovery of Polysaccharides and Polyphenols from Winery Effluents. Sep. Sci. Technol. 2013, 48, 438–444. [Google Scholar] [CrossRef]
- da Trindade, C.D.M.; Giacobbo, A.; Ferreira, V.G.; Rodrigues, M.A.S.; Bernardes, A.M. Membrane separation processes applied to the treatment of effluents from nanoceramic coating operations. Desalin. Water Treat. 2015, 55, 28–38. [Google Scholar] [CrossRef]
- Wilson, A.D.; Stewart, F.F. Deriving osmotic pressures of draw solutes used in osmotically driven membrane processes. J. Memb. Sci. 2013, 431, 205–211. [Google Scholar] [CrossRef]
- Venzke, C.D.; Giacobbo, A.; Klauck, C.R.; Viegas, C.; Hansen, E.; Monteiro de Aquim, P.; Rodrigues, M.A.S.; Bernardes, A.M. Integrated membrane processes (EDR-RO) for water reuse in the petrochemical industry. J. Membr. Sci. Res. 2018, 4, 218–226. [Google Scholar]
- Chem Axon Chemicalize. Instant Cheminformatics Solutions. Chemicalize calculation module developed by ChemAxon. Chemicalize was used for sulfametoxazole and norfloxacin, properties and microspeciation in aqueous solution as a function of pH. Available online: https://chemicalize.com (accessed on 10 June 2020).
- Kong, F.X.; Yang, H.W.; Wu, Y.Q.; Wang, X.M.; Xie, Y.F. Rejection of pharmaceuticals during forward osmosis and prediction by using the solution-diffusion model. J. Memb. Sci. 2015, 476, 410–420. [Google Scholar] [CrossRef]
- APHA—American Public Health Association. Standard Methods for the Examination of Water and Wastewater, 21th ed.; Amercian Public Health Association: Washingtion, DC, USA, 2005. [Google Scholar]
- de Souza, D.I.; Dottein, E.M.; Giacobbo, A.; Rodrigues, M.A.S.; de Pinho, M.N.; Bernardes, A.M. Nanofiltration for the removal of norfloxacin from pharmaceutical effluent. J. Environ. Chem. Eng. 2018, 6, 6147–6153. [Google Scholar] [CrossRef]
- Giacobbo, A.; Bernardes, A.M.; de Pinho, M.N. Sequential pressure-driven membrane operations to recover and fractionate polyphenols and polysaccharides from second racking wine lees. Sep. Purif. Technol. 2017, 173, 49–54. [Google Scholar] [CrossRef]
- Giacobbo, A.; Bernardes, A.M.; Rosa, M.J.F.; de Pinho, M.N. Concentration polarization in ultrafiltration/nanofiltration for the recovery of polyphenols from winery wastewaters. Membranes 2018, 8, 46. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bellona, C.; Drewes, J.E.; Xu, P.; Amy, G. Factors affecting the rejection of organic solutes during NF/RO treatment—a literature review. Water Res. 2004, 38, 2795–2809. [Google Scholar] [CrossRef]
- Nghiem, L.D.; Schäfer, A.I.; Elimelech, M. Pharmaceutical retention mechanisms by nanofiltration membranes. Environ. Sci. Technol. 2005, 39, 7698–7705. [Google Scholar] [CrossRef]
- Hidalgo, A.M.; León, G.; Gómez, M.; Murcia, M.D.; Gómez, E.; Gómez, J.L. Application of the Spiegler–Kedem–Kachalsky model to the removal of 4-chlorophenol by different nanofiltration membranes. Desalination 2013, 315, 70–75. [Google Scholar] [CrossRef]
- Cheng, X.Q.; Liu, Y.; Guo, Z.; Shao, L. Nanofiltration membrane achieving dual resistance to fouling and chlorine for “green” separation of antibiotics. J. Memb. Sci. 2015, 493, 156–166. [Google Scholar] [CrossRef]
- Baker, R.W. Membrane Technology and Applications, 2nd ed.; John Wiley & Sons: West Sussex, UK, 2012; ISBN 0470854456. [Google Scholar]
- Solomons, T.W.G.; Fryhle, C. Organic Chemistry, 6th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Dolar, D.; Vuković, A.; Ašperger, D.; Košutić, K. Effect of water matrices on removal of veterinary pharmaceuticals by nanofiltration and reverse osmosis membranes. J. Environ. Sci. 2011, 23, 1299–1307. [Google Scholar] [CrossRef]
- Kim, S.; Chu, K.H.; Al-Hamadani, Y.A.J.; Park, C.M.; Jang, M.; Kim, D.-H.; Yu, M.; Heo, J.; Yoon, Y. Removal of contaminants of emerging concern by membranes in water and wastewater: A review. Chem. Eng. J. 2018, 335, 896–914. [Google Scholar] [CrossRef]
- Thanuttamavong, M.; Yamamoto, K.; Ik Oh, J.; Ho Choo, K.; June Choi, S. Rejection characteristics of organic and inorganic pollutants by ultra low-pressure nanofiltration of surface water for drinking water treatment. Desalination 2002, 145, 257–264. [Google Scholar] [CrossRef]






| Physicochemical Characteristic | NOR | SMX |
|---|---|---|
| Molecular formula 1 | C16H18FN3O3 | C10H11N3O3S |
| Molecular weight 1 (Da) | 319.33 | 253.28 |
| Structural formula 1 |  |  |
| pKa 1 | 5.58; 8.68 | 1.97; 6.16 |
| log KOW 2 | −1.03 | −0.89 |
| Polarisability 1 (A°) | 31.15 | 24.16 |
| Stokes radius 2 (nm) | 0.47 | 0.39 |
| Diffusion coefficient (10−1 m2 s−1)2 | 5.22 | 6.25 |
| Factor | Level (−1) | Level (+1) |
|---|---|---|
| A, Antibiotic MW (Da) | 253 | 319 |
| B, Feed flow rate (L h−1) | 480 1 | 850 2 |
| C, Concentration (mg L−1) | 5 | 25 |
| D, Membrane MWCO (Da) | 200 | 400 |
| E, Transmembrane pressure (bar) | 6 | 16 |
| Parameter | NF Feed Wastewater 1 |
|---|---|
| pH | 6.01 ± 0.11 |
| Conductivity (µS cm−1) | 428 ± 14.1 |
| Total solids (mg L−1) | 539 ± 139 |
| Total suspended solids (mg L−1) | 3.90 ± 0.60 |
| Dissolved organic carbon – DOC (mg L−1) | 8.50 ± 0.40 |
| Chemical oxygen demand – COD (mg O2 L−1) | 184 ± 192 |
| NOR (mg L−1) | 9.40 ± 3.00 |
| SMX (mg L−1) | 9.10 ± 1.40 |
| Antibiotic | MW (Da) | Concentration (mg L−1) | QF (L h−1) | NF97 | NF270 | ||
|---|---|---|---|---|---|---|---|
| LPS 1 | LPW− LPS (%) | LPS 1 | LPW− LPS (%) | ||||
| NOR | 319 | 5 | 480 | 2.99 ± 0.05 | 3.55 | 8.40 ± 0.10 | 4.22 |
| 5 | 850 | 3.04 ± 0.22 | 1.94 | 8.29 ± 0.23 | 5.47 | ||
| 25 | 480 | 2.90 ± 0.13 | 6.45 | 7.91 ± 0.15 | 9.81 | ||
| 25 | 850 | 3.01 ± 0.05 | 2.90 | 7.89 ± 0.13 | 10.0 | ||
| SMX | 253 | 5 | 480 | 3.01 ± 0.01 | 2.90 | 8.93 ± 0.01 | −1.82 |
| 5 | 850 | 3.20 ± 0.02 | −3.23 | 9.25 ± 0.04 | −5.47 | ||
| 25 | 480 | 2.75 ± 0.08 | 11.3 | 8.58 ± 0.45 | 2.17 | ||
| 25 | 850 | 3.04 ± 1.94 | 1.94 | 8.49 ± 0.57 | 3.19 | ||
| Antibiotic | MW (Da) | Concentration (mg L−1) | QF (L h−1) | R (%) | |
|---|---|---|---|---|---|
| NF97 | NF270 | ||||
| NOR | 319 | 5 | 480 | 99.6 ± 0.3 | 95.6 ± 1.0 |
| 5 | 850 | 99.0 ± 0.4 | 95.2 ± 0.4 | ||
| 25 | 480 | 98.7 ± 0.3 | 96.8 ± 0.8 | ||
| 25 | 850 | 89.2 ± 3.0 | 95.0 ± 0.7 | ||
| SMX | 253 | 5 | 480 | 98.4 ± 0.1 | 65.3 ± 1.0 |
| 5 | 850 | 98.4 ± 0.1 | 65.4 ± 2.0 | ||
| 25 | 480 | 98.4 ± 0.1 | 63.3 ± 3.0 | ||
| 25 | 850 | 98.6 ± 0.1 | 69.1 ± 1.1 | ||
| Antibiotic | Membrane | Water Recovery (%) | Permeate Flux (kg h−1 m−2 bar−1) | Rejection (%) | ||
|---|---|---|---|---|---|---|
| Experimental | Predicted | Experimental | Predicted | |||
| NOR | NF97 | 65 | 12.7 | 19.27 | 98.08 | 98.72 |
| 70 | 12.5 | 19.27 | 98.64 | 98.72 | ||
| NF270 | 65 | 38.5 | 55.88 | 97.06 | 97.22 | |
| 70 | 38.2 | 55.88 | 96.47 | 97.22 | ||
| SMX | NF97 | 65 | 12.66 | 19.22 | 97.80 | 98.39 |
| 70 | 12.45 | 19.22 | 98.01 | 98.39 | ||
| NF270 | 65 | 38.52 | 56.72 | 96.26 | 63.47 | |
| 70 | 38.14 | 56.76 | 97.01 | 63.47 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Souza, D.I.; Giacobbo, A.; da Silva Fernandes, E.; Rodrigues, M.A.S.; de Pinho, M.N.; Bernardes, A.M. Experimental Design as a Tool for Optimizing and Predicting the Nanofiltration Performance by Treating Antibiotic-Containing Wastewater. Membranes 2020, 10, 156. https://doi.org/10.3390/membranes10070156
de Souza DI, Giacobbo A, da Silva Fernandes E, Rodrigues MAS, de Pinho MN, Bernardes AM. Experimental Design as a Tool for Optimizing and Predicting the Nanofiltration Performance by Treating Antibiotic-Containing Wastewater. Membranes. 2020; 10(7):156. https://doi.org/10.3390/membranes10070156
Chicago/Turabian Stylede Souza, Dalva Inês, Alexandre Giacobbo, Eduardo da Silva Fernandes, Marco Antônio Siqueira Rodrigues, Maria Norberta de Pinho, and Andréa Moura Bernardes. 2020. "Experimental Design as a Tool for Optimizing and Predicting the Nanofiltration Performance by Treating Antibiotic-Containing Wastewater" Membranes 10, no. 7: 156. https://doi.org/10.3390/membranes10070156
APA Stylede Souza, D. I., Giacobbo, A., da Silva Fernandes, E., Rodrigues, M. A. S., de Pinho, M. N., & Bernardes, A. M. (2020). Experimental Design as a Tool for Optimizing and Predicting the Nanofiltration Performance by Treating Antibiotic-Containing Wastewater. Membranes, 10(7), 156. https://doi.org/10.3390/membranes10070156