Theoretical Evaluation of Polyelectrolyte Layering during Layer-by-Layer Coating of Ultrafiltration Hollow Fiber Membranes
Abstract
:1. Introduction
1.1. Layer-by-Layer Process and Influences
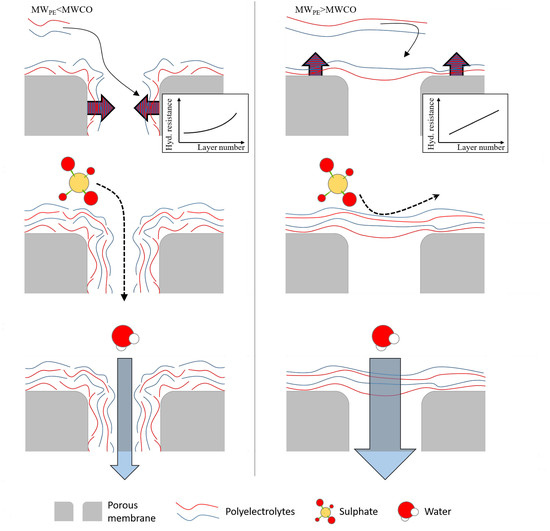
1.2. Membrane Fouling and Modeling
1.3. Standard Blocking Model
1.4. Cake Layer Formation
2. Materials and Methods
2.1. Materials
2.2. Membrane
2.3. Modification
2.4. Filtration Setup
2.5. Fluorescence Measurement
3. Development of the Layering Model
4. Results and Discussion
4.1. Normalized Flux, Hydraulic Resistance, and Share Factor
4.2. Plausibility of the Model
4.3. Rejection for MgSO4
4.4. Fluorescence Measurement
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ang, W.L.; Mohammad, A.W.; Hilal, N.; Leo, C.P. A review on the applicability of integrated/hybrid membrane processes in water treatment and desalination plants. Desalination 2015, 363, 2–18. [Google Scholar] [CrossRef]
- Mohammad, A.W.; Teow, Y.H.; Ang, W.L.; Chung, Y.T.; Oatley-Radcliffe, D.L.; Hilal, N. Nanofiltration membranes review: Recent advances and future prospects. Desalination 2015, 356, 226–254. [Google Scholar] [CrossRef]
- Gao, Y.; Qin, J.; Wang, Z.; Østerhus, S.W. Backpulsing technology applied in MF and UF processes for membrane fouling mitigation: A review. J. Membr. Sci. 2019, 587, 117136. [Google Scholar] [CrossRef]
- Racar, M.; Dolar, D.; Špehar, A.; Košutić, K. Application of UF/NF/RO membranes for treatment and reuse of rendering plant wastewater. Process Saf. Environ. Prot. 2017, 105, 386–392. [Google Scholar] [CrossRef]
- Joseph, N.; Ahmadiannamini, P.; Hoogenboom, R.; Vankelecom, I.F.J. Layer-by-layer preparation of polyelectrolyte multilayer membranes for separation. Polym. Chem. 2014, 5, 1817–1831. [Google Scholar] [CrossRef]
- Menne, D.; Üzüm, C.; Koppelmann, A.; Wong, J.E.; van Foeken, C.; Borre, F.; Dähne, L.; Laakso, T.; Pihlajamäki, A.; Wessling, M. Regenerable polymer/ceramic hybrid nanofiltration membrane based on polyelectrolyte assembly by layer-by-layer technique. J. Membr. Sci. 2016, 520, 924–932. [Google Scholar] [CrossRef]
- De Grooth, J.; Haakmeester, B.; Wever, C.; Potreck, J.; de Vos, W.M.; Nijmeijer, K. Long term physical and chemical stability of polyelectrolyte multilayer membranes. J. Membr. Sci. 2015, 489, 153–159. [Google Scholar] [CrossRef]
- Su, B.; Wang, T.; Wang, Z.; Gao, X.; Gao, C. Preparation and performance of dynamic layer-by-layer PDADMAC/PSS nanofiltration membrane. J. Membr. Sci. 2012, 423–424, 324–331. [Google Scholar] [CrossRef]
- Guzmán, E.; Ritacco, H.; Ortega, F.; Svitova, T.; Radke, C.J.; Rubio, R.G. Adsorption kinetics and mechanical properties of ultrathin polyelectrolyte multilayers: Liquid-supported versus solid-supported films. J. Phys. Chem. B 2009, 113, 7128–7137. [Google Scholar] [CrossRef]
- Cherstvy, A.G. Electrostatics and Charge Regulation in Polyelectrolyte Multilayered Assembly. J. Phys. Chem. B 2014, 118, 4552–4560. [Google Scholar] [CrossRef]
- Dubas, S.T.; Schlenoff, J.B. Factors Controlling the Growth of Polyelectrolyte Multilayers. Macromolecules 1999, 32, 8153–8160. [Google Scholar] [CrossRef]
- De Grooth, J.; Oborný, R.; Potreck, J.; Nijmeijer, K.; de Vos, W.M. The role of ionic strength and odd–even effects on the properties of polyelectrolyte multilayer nanofiltration membranes. J. Membr. Sci. 2015, 475, 311–319. [Google Scholar] [CrossRef]
- McAloney, R.A.; Sinyor, M.; Dudnik, V.; Goh, M.C. Atomic Force Microscopy Studies of Salt Effects on Polyelectrolyte Multilayer Film Morphology. Langmuir 2001, 17, 6655–6663. [Google Scholar] [CrossRef]
- Guzmán, E.; Ritacco, H.; Rubio, J.E.F.; Rubio, R.G.; Ortega, F. Salt-induced changes in the growth of polyelectrolyte layers of poly(diallyl-dimethylammonium chloride) and poly(4-styrene sulfonate of sodium). Soft Matter 2009, 5, 2130. [Google Scholar] [CrossRef]
- Menne, D. Entwicklung von “Layer-by-Layer” Nanofiltrationsmembranen. Ph.D. Thesis, Rheinisch-Westfälische Technische Hochschule Aachen, Aachen, Germany, 2017. [Google Scholar]
- Reurink, D.M.; Haven, J.P.; Achterhuis, I.; Lindhoud, S.; Roesink, E.H.D.W.; de Vos, W.M. Annealing of Polyelectrolyte Multilayers for Control over Ion Permeation. Adv. Mater. Interfaces 2018, 5, 1800651. [Google Scholar] [CrossRef] [Green Version]
- Tang, K.; Besseling, N.A.M. Formation of polyelectrolyte multilayers: Ionic strengths and growth regimes. Soft Matter 2016, 12, 1032–1040. [Google Scholar] [CrossRef] [Green Version]
- Elżbieciak-Wodka, M.; Kolasińska-Sojka, M.; Warszyński, P. Effect of mono- and divalent ions on the formation and permeability of polyelectrolyte multilayer films. J. Electroanal. Chem. 2017, 789, 123–132. [Google Scholar] [CrossRef]
- Wong, J.E.; Zastrow, H.; Jaeger, W.; von Klitzing, R. Specific ion versus electrostatic effects on the construction of polyelectrolyte multilayers. Langmuir 2009, 25, 14061–14070. [Google Scholar] [CrossRef]
- Nestler, P.; Paßvogel, M.; Helm, C.A. Influence of Polymer Molecular Weight on the Parabolic and Linear Growth Regime of PDADMAC/PSS Multilayers. Macromolecules 2013, 46, 5622–5629. [Google Scholar] [CrossRef]
- Soltwedel, O.; Nestler, P.; Neumann, H.-G.; Paßvogel, M.; Köhler, R.; Helm, C.A. Influence of Polycation (PDADMAC) Weight on Vertical Diffusion within Polyelectrolyte Multilayers during Film Formation and Postpreparation Treatment. Macromolecules 2012, 45, 7995–8004. [Google Scholar] [CrossRef]
- Harris, J.J.; Stair, J.L.; Bruening, M.L. Layered Polyelectrolyte Films as Selective, Ultrathin Barriers for Anion Transport. Chem. Mater. 2000, 12, 1941–1946. [Google Scholar] [CrossRef]
- Malaisamy, R.; Bruening, M.L. High-flux nanofiltration membranes prepared by adsorption of multilayer polyelectrolyte membranes on polymeric supports. Langmuir 2005, 21, 10587–10592. [Google Scholar] [CrossRef]
- Liu, C.; Shi, L.; Wang, R. Enhanced hollow fiber membrane performance via semi-dynamic layer-by-layer polyelectrolyte inner surface deposition for nanofiltration and forward osmosis applications. React. Funct. Polym. 2015, 86, 154–160. [Google Scholar] [CrossRef]
- Miller, M.D.; Bruening, M.L. Correlation of the Swelling and Permeability of Polyelectrolyte Multilayer Films. Chem. Mater. 2005, 17, 5375–5381. [Google Scholar] [CrossRef]
- McCormick, M.; Smith, R.N.; Graf, R.; Barrett, C.J.; Reven, L.; Spiess, H.W. NMR Studies of the Effect of Adsorbed Water on Polyelectrolyte Multilayer Films in the Solid State. Macromolecules 2003, 36, 3616–3625. [Google Scholar] [CrossRef]
- Schwarz, B.; Schönhoff, M. Surface Potential Driven Swelling of Polyelectrolyte Multilayers. Langmuir 2002, 18, 2964–2966. [Google Scholar] [CrossRef]
- Xiao, K.; Wang, X.; Huang, X.; Waite, T.D.; Wen, X. Combined effect of membrane and foulant hydrophobicity and surface charge on adsorptive fouling during microfiltration. J. Membr. Sci. 2011, 373, 140–151. [Google Scholar] [CrossRef]
- Iritani, E. A Review on Modeling of Pore-Blocking Behaviors of Membranes During Pressurized Membrane Filtration. Dry. Technol. 2013, 31, 146–162. [Google Scholar] [CrossRef]
- Ho, Z. A Combined Pore Blockage and Cake Filtration Model for Protein Fouling during Microfiltration. J. Colloid Interface Sci. 2000, 232, 389–399. [Google Scholar] [CrossRef]
- Lee, S.; Park, P.-K.; Kim, J.-H.; Yeon, K.-M.; Lee, C.-H. Analysis of filtration characteristics in submerged microfiltration for drinking water treatment. Water Res. 2008, 42, 3109–3121. [Google Scholar] [CrossRef]
- Davis, R.H. Modeling of Fouling of Crossflow Microfiltration Membranes. Sep. Purif. Methods 1992, 21, 75–126. [Google Scholar] [CrossRef]
- Crittenden, J.C. MWH’s Water Treatment. Principles and Design, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2012; ISBN 0470405392. [Google Scholar]
- Usman, M.; Katsoyiannis, I.; Mitrakas, M.; Zouboulis, A.; Ernst, M. Performance Evaluation of Small Sized Powdered Ferric Hydroxide as Arsenic Adsorbent. Water 2018, 10, 957. [Google Scholar] [CrossRef] [Green Version]
- Lyu, X.; Peterson, A.M. The Princess and the Pea Effect: Influence of the first layer on polyelectrolyte multilayer assembly and properties. J. Colloid Interface Sci. 2017, 502, 165–171. [Google Scholar] [CrossRef]
- Adusumilli, M.; Bruening, M.L. Variation of ion-exchange capacity, zeta potential, and ion-transport selectivities with the number of layers in a multilayer polyelectrolyte film. Langmuir 2009, 25, 7478–7485. [Google Scholar] [CrossRef]
- Dillmann, S.; Kaushik, S.A.; Stumme, J.; Ernst, M. Characterization and Performance of LbL-Coated Multibore Membranes: Zeta Potential, MWCO, Permeability and Sulfate Rejection. Membranes 2020, 10, 412. [Google Scholar] [CrossRef]







| Parameter | Abbreviation | Unit | MB220 | MB100 |
|---|---|---|---|---|
| Active layer thickness/pore length | 2 | 2 | ||
| Capillary diameter | 0.9 | 0.9 | ||
| Molecular weight cut-off | 220 | 100 | ||
| Initial pore diameter | 36 | 22 | ||
| Number of pores per unit of active area | 2.85 | 7.63 | ||
| Porosity | 29 | 29 |
| Assumed Parameters | Unit | M_220-PSS | M_100-PSS | M_100-PDADMAC |
|---|---|---|---|---|
| Dynamic viscosity (η) | 1.002 | |||
| Thickness per double layer ( | 4.0 | |||
| Mass deposited per layer ( | 0.25 | |||
| Fitted parameters | ||||
| Standard blocking constant () | 7.9 | 4.0 | 2.5 | |
| Specific cake resistance () | 46.2 | 20.6 | 7.3 | |
| Transition coefficient a () | 10.5 | 4.0 | 4.0 | |
| Transition coefficient b () | 3.0 | 4.5 | 4.5 | |
| Resulting correlation coefficient and chi-squared value | ||||
| Correlation coefficient resistance () | 0.999 | 00.994 | 0.992 | |
| Chi-squared value () | 0.86 | 0.75 | 0.62 | |
| Correlation coefficient resistance () | 0.995 | 0.994 | 0.991 | |
| Chi-squared value () | 1.33 | 0.25 | 0.37 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stumme, J.; Ashokkumar, O.; Dillmann, S.; Niestroj-Pahl, R.; Ernst, M. Theoretical Evaluation of Polyelectrolyte Layering during Layer-by-Layer Coating of Ultrafiltration Hollow Fiber Membranes. Membranes 2021, 11, 106. https://doi.org/10.3390/membranes11020106
Stumme J, Ashokkumar O, Dillmann S, Niestroj-Pahl R, Ernst M. Theoretical Evaluation of Polyelectrolyte Layering during Layer-by-Layer Coating of Ultrafiltration Hollow Fiber Membranes. Membranes. 2021; 11(2):106. https://doi.org/10.3390/membranes11020106
Chicago/Turabian StyleStumme, Jakob, Omjothi Ashokkumar, Saskia Dillmann, Robert Niestroj-Pahl, and Mathias Ernst. 2021. "Theoretical Evaluation of Polyelectrolyte Layering during Layer-by-Layer Coating of Ultrafiltration Hollow Fiber Membranes" Membranes 11, no. 2: 106. https://doi.org/10.3390/membranes11020106
APA StyleStumme, J., Ashokkumar, O., Dillmann, S., Niestroj-Pahl, R., & Ernst, M. (2021). Theoretical Evaluation of Polyelectrolyte Layering during Layer-by-Layer Coating of Ultrafiltration Hollow Fiber Membranes. Membranes, 11(2), 106. https://doi.org/10.3390/membranes11020106