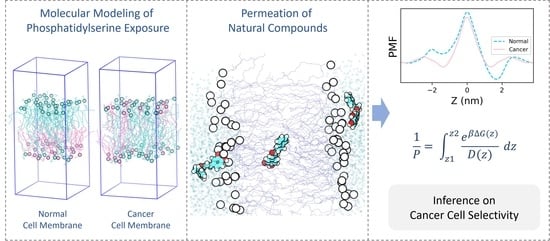
Phosphatidylserine Exposed Lipid Bilayer Models for Understanding Cancer Cell Selectivity of Natural Compounds: A Molecular Dynamics Simulation Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Generation of Lipid Bilayer Systems
2.2. Equilibration of Lipid Bilayer Systems
2.3. Calculation of Membrane Properties
2.4. Steered Molecular Dynamics Simulations and Umbrella Sampling
2.5. Calculation of PMF and Permeability Coefficients
3. Results and Discussion
3.1. Structural Properties of Lipid Bilayer Systems
3.2. PMF Profiles of the Natural Compounds
3.3. Resistivity Profiles of the Natural Compounds
3.4. Permeability Coefficients of the Natural Compounds
3.5. Implications of the Study
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chari, R.V. Targeted cancer therapy: Conferring specificity to cytotoxic drugs. Acc. Chem. Res. 2008, 41, 98–107. [Google Scholar] [CrossRef] [PubMed]
- Coates, A.; Abraham, S.; Kaye, S.B.; Sowerbutts, T.; Frewin, C.; Fox, R.; Tattersall, M. On the receiving end—Patient perception of the side-effects of cancer chemotherapy. Eur. J. Cancer Clin. Oncol. 1983, 19, 203–208. [Google Scholar] [CrossRef]
- Escribá, P.V. Membrane-lipid therapy: A new approach in molecular medicine. Trends Mol. Med. 2006, 12, 34–43. [Google Scholar] [CrossRef]
- Alves, A.C.; Ribeiro, D.; Nunes, C.; Reis, S. Biophysics in cancer: The relevance of drug-membrane interaction studies. Biochim. Biophys. Acta (BBA)-Biomembr. 2016, 1858, 2231–2244. [Google Scholar] [CrossRef] [PubMed]
- Azordegan, N.; Fraser, V.; Le, K.; Hillyer, L.M.; Ma, D.W.; Fischer, G.; Moghadasian, M.H. Carcinogenesis alters fatty acid profile in breast tissue. Mol. Cell. Biochem. 2013, 374, 223–232. [Google Scholar] [CrossRef]
- Merchant, T.; Kasimos, J.; De Graaf, P.; Minsky, B.; Gierke, L.; Glonek, T. Phospholipid profiles of human colon cancer using 31 P magnetic resonance spectroscopy. Int. J. Colorectal Dis. 1991, 6, 121–126. [Google Scholar] [CrossRef] [PubMed]
- Selkirk, J.K.; Elwood, J.; Morris, H. Study on the proposed role of phospholipid in tumor cell membrane. Cancer Res. 1971, 31, 27–31. [Google Scholar] [PubMed]
- Hildebrand, J.; Marique, D.; Vanhouche, J. Lipid composition of plasma membranes from human leukemic lymphocytes. J. Lipid Res. 1975, 16, 195–199. [Google Scholar] [CrossRef]
- Liebes, L.F.; Pelle, E.; Zucker-Franklin, D.; Silber, R. Comparison of lipid composition and 1, 6-diphenyl-1, 3, 5-hexatriene fluorescence polarization measurements of hairy cells with monocytes and lymphocytes from normal subjects and patients with chronic lymphocytic leukemia. Cancer Res. 1981, 41, 4050–4056. [Google Scholar] [PubMed]
- Baro, L.; Hermoso, J.; Nunez, M.; Jimenez-Rios, J.; Gil, A. Abnormalities in plasma and red blood cell fatty acid profiles of patients with colorectal cancer. Br. J. Cancer 1998, 77, 1978–1983. [Google Scholar] [CrossRef]
- Ran, S.; Downes, A.; Thorpe, P.E. Increased exposure of anionic phospholipids on the surface of tumor blood vessels. Cancer Res. 2002, 62, 6132–6140. [Google Scholar] [PubMed]
- Ran, S.; Thorpe, P.E. Phosphatidylserine is a marker of tumor vasculature and a potential target for cancer imaging and therapy. Int. J. Radiat. Oncol. Biol. Phys. 2002, 54, 1479–1484. [Google Scholar] [CrossRef]
- Stafford, J.H.; Thorpe, P.E. Increased exposure of phosphatidylethanolamine on the surface of tumor vascular endothelium. Neoplasia 2011, 13, 299–308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verkleij, A.; Zwaal, R.; Roelofsen, B.; Comfurius, P.; Kastelijn, D.; Van Deenen, L. The asymmetric distribution of phospholipids in the human red cell membrane. A combined study using phospholipases and freeze-etch electron microscopy. Biochim. Biophys. Acta (BBA)-Biomembr. 1973, 323, 178–193. [Google Scholar] [CrossRef]
- Yamaji-Hasegawa, A.; Tsujimoto, M. Asymmetric distribution of phospholipids in biomembranes. Biol. Pharm. Bull. 2006, 29, 1547–1553. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clark, M.R. Flippin’lipids. Nat. Immunol. 2011, 12, 373–375. [Google Scholar] [CrossRef] [PubMed]
- Gurtovenko, A.A.; Vattulainen, I. Lipid transmembrane asymmetry and intrinsic membrane potential: Two sides of the same coin. J. Am. Chem. Soc. 2007, 129, 5358–5359. [Google Scholar] [CrossRef]
- Gurtovenko, A.A.; Vattulainen, I. Membrane potential and electrostatics of phospholipid bilayers with asymmetric transmembrane distribution of anionic lipids. J. Phys. Chem. B 2008, 112, 4629–4634. [Google Scholar] [CrossRef] [Green Version]
- Falkovich, S.G.; Martinez-Seara, H.; Nesterenko, A.M.; Vattulainen, I.; Gurtovenko, A.A. What Can We Learn about Cholesterol’s Transmembrane Distribution Based on Cholesterol-Induced Changes in Membrane Dipole Potential? J. Phys. Chem. Lett. 2016, 7, 4585–4590. [Google Scholar] [CrossRef] [PubMed]
- López Cascales, J.; Otero, T.; Smith, B.D.; Gonzalez, C.; Marquez, M. Model of an asymmetric DPPC/DPPS membrane: Effect of asymmetry on the lipid properties. A molecular dynamics simulation study. J. Phys. Chem. B 2006, 110, 2358–2363. [Google Scholar] [CrossRef]
- Orsi, M.; Sanderson, W.E.; Essex, J.W. Permeability of small molecules through a lipid bilayer: A multiscale simulation study. J. Phys. Chem. B 2009, 113, 12019–12029. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thai, N.Q.; Theodorakis, P.E.; Li, M.S. Fast Estimation of the Blood–Brain Barrier Permeability by Pulling a Ligand through a Lipid Membrane. J. Chem. Inf. Model. 2020, 60, 3057–3067. [Google Scholar] [CrossRef] [PubMed]
- Wadhwa, R.; Yadav, N.S.; Katiyar, S.P.; Yaguchi, T.; Lee, C.; Ahn, H.; Yun, C.-O.; Kaul, S.C.; Sundar, D. Molecular dynamics simulations and experimental studies reveal differential permeability of withaferin-A and withanone across the model cell membrane. Sci. Rep. 2021, 11, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Dickson, C.J.; Hornak, V.; Bednarczyk, D.; Duca, J.S. Using Membrane Partitioning Simulations to Predict Permeability of Forty-Nine Drug-Like Molecules. J. Chem. Inf. Model. 2019, 59, 236–244. [Google Scholar] [CrossRef]
- Bhargava, P.; Malik, V.; Liu, Y.; Ryu, J.; Kaul, S.C.; Sundar, D.; Wadhwa, R. Molecular insights into withaferin-A-induced senescence: Bioinformatics and experimental evidence to the role of NFκB and CARF. J. Gerontol. Ser. A 2019, 74, 183–191. [Google Scholar] [CrossRef]
- Sari, A.N.; Bhargava, P.; Dhanjal, J.K.; Putri, J.F.; Radhakrishnan, N.; Shefrin, S.; Ishida, Y.; Terao, K.; Sundar, D.; Kaul, S.C. Combination of withaferin-A and CAPE provides superior anticancer potency: Bioinformatics and experimental evidence to their molecular targets and mechanism of action. Cancers 2020, 12, 1160. [Google Scholar] [CrossRef]
- Garg, S.; Huifu, H.; Kumari, A.; Sundar, D.; Kaul, S.C.; Wadhwa, R. Induction of senescence in cancer cells by a novel combination of Cucurbitacin B and withanone: Molecular mechanism and therapeutic potential. J. Gerontol. Ser. A 2020, 75, 1031–1041. [Google Scholar] [CrossRef] [PubMed]
- Malik, V.; Kumar, V.; Kaul, S.C.; Wadhwa, R.; Sundar, D. Computational Insights into the Potential of Withaferin-A, Withanone and Caffeic Acid Phenethyl Ester for Treatment of Aberrant-EGFR Driven Lung Cancers. Biomolecules 2021, 11, 160. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Katiyar, S.P.; Sundar, D.; Kaul, Z.; Miyako, E.; Zhang, Z.; Kaul, S.C.; Reddel, R.R.; Wadhwa, R. Withaferin-A kills cancer cells with and without telomerase: Chemical, computational and experimental evidences. Cell Death Dis. 2017, 8, e2755. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, R.; Shah, N.; Lee, J.-S.; Katiyar, S.P.; Li, L.; Oh, E.; Sundar, D.; Yun, C.-O.; Wadhwa, R.; Kaul, S.C. Withanone-rich combination of Ashwagandha withanolides restricts metastasis and angiogenesis through hnRNP-K. Mol. Cancer Ther. 2014, 13, 2930–2940. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vaishnavi, K.; Saxena, N.; Shah, N.; Singh, R.; Manjunath, K.; Uthayakumar, M.; Kanaujia, S.P.; Kaul, S.C.; Sekar, K.; Wadhwa, R. Differential Activities of the Two Closely Related Withanolides, Withaferin A and Withanone: Bioinformatics and Experimental Evidences. PLoS ONE 2012, 7, e44419. [Google Scholar] [CrossRef] [Green Version]
- Kimoto, T.; Arai, S.; Kohguchi, M.; Aga, M.; Nomura, Y.; Micallef, M.J.; Kurimoto, M.; Mito, K. Apoptosis and suppression of tumor growth by artepillin C extracted from Brazilian propolis. Cancer Detect. Prev. 1998, 22, 506–515. [Google Scholar] [CrossRef]
- Szliszka, E.; Zydowicz, G.; Mizgala, E.; Krol, W. Artepillin C (3,5-diprenyl-4-hydroxycinnamic acid) sensitizes LNCaP prostate cancer cells to TRAIL-induced apoptosis. Int. J. Oncol. 2012, 41, 818–828. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Souza, R.P.; Bonfim-Mendonça, P.S.; Damke, G.M.; de-Assis Carvalho, A.R.; Ratti, B.A.; Dembogurski, D.S.; da-Silva, V.R.; Silva, S.O.; Da-Silva, D.B.; Bruschi, M.L. Artepillin C induces selective oxidative stress and inhibits migration and invasion in a comprehensive panel of human cervical cancer cell lines. Anti-Cancer Agents Med. Chem. 2018, 18, 1750–1760. [Google Scholar] [CrossRef] [PubMed]
- Diamond, J.M.; Katz, Y. Interpretation of nonelectrolyte partition coefficients between dimyristoyl lecithin and water. J. Membr. Biol. 1974, 17, 121–154. [Google Scholar] [CrossRef]
- Marrink, S.-J.; Berendsen, H.J. Simulation of water transport through a lipid membrane. J. Phys. Chem. 1994, 98, 4155–4168. [Google Scholar] [CrossRef] [Green Version]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Meng, F.; Xu, W. Drug permeability prediction using PMF method. J. Mol. Model. 2013, 19, 991–997. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.T.; Comer, J.; Herndon, C.; Leung, N.; Pavlova, A.; Swift, R.V.; Tung, C.; Rowley, C.N.; Amaro, R.E.; Chipot, C. Simulation-based approaches for determining membrane permeability of small compounds. J. Chem. Inf. Model. 2016, 56, 721–733. [Google Scholar] [CrossRef] [Green Version]
- DeMarco, K.R.; Bekker, S.; Clancy, C.E.; Noskov, S.Y.; Vorobyov, I. Digging into lipid membrane permeation for cardiac ion channel blocker d-sotalol with all-atom simulations. Front. Pharmacol. 2018, 9, 26. [Google Scholar] [CrossRef] [Green Version]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berendsen, H.J.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Guixà-González, R.; Rodriguez-Espigares, I.; Ramírez-Anguita, J.M.; Carrió-Gaspar, P.; Martinez-Seara, H.; Giorgino, T.; Selent, J. MEMBPLUGIN: Studying membrane complexity in VMD. Bioinformatics 2014, 30, 1478–1480. [Google Scholar] [CrossRef] [Green Version]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Gr. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. (TOMS) 1996, 22, 469–483. [Google Scholar] [CrossRef] [Green Version]
- Vermeer, L.S.; De Groot, B.L.; Réat, V.; Milon, A.; Czaplicki, J. Acyl chain order parameter profiles in phospholipid bilayers: Computation from molecular dynamics simulations and comparison with 2 H NMR experiments. Eur. Biophys. J. 2007, 36, 919–931. [Google Scholar] [CrossRef] [Green Version]
- Hummer, G. Position-dependent diffusion coefficients and free energies from Bayesian analysis of equilibrium and replica molecular dynamics simulations. New J. Phys. 2005, 7. [Google Scholar] [CrossRef]
- Utsugi, T.; Schroit, A.J.; Connor, J.; Bucana, C.D.; Fidler, I.J. Elevated expression of phosphatidylserine in the outer membrane leaflet of human tumor cells and recognition by activated human blood monocytes. Cancer Res. 1991, 51, 3062–3066. [Google Scholar]
- Riedl, S.; Rinner, B.; Asslaber, M.; Schaider, H.; Walzer, S.; Novak, A.; Lohner, K.; Zweytick, D. In search of a novel target—Phosphatidylserine exposed by non-apoptotic tumor cells and metastases of malignancies with poor treatment efficacy. Biochim. Biophys. Acta (BBA)-Biomembr. 2011, 1808, 2638–2645. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lopes, D.; Jakobtorweihen, S.; Nunes, C.; Sarmento, B.; Reis, S. Shedding light on the puzzle of drug-membrane interactions: Experimental techniques and molecular dynamics simulations. Prog. Lipid Res. 2017, 65, 24–44. [Google Scholar] [CrossRef]
- Moradi, S.; Nowroozi, A.; Shahlaei, M. Shedding light on the structural properties of lipid bilayers using molecular dynamics simulation: A review study. RSC Adv. 2019, 9, 4644–4658. [Google Scholar] [CrossRef] [Green Version]
- Klauda, J.B.; Venable, R.M.; Freites, J.A.; O’Connor, J.W.; Tobias, D.J.; Mondragon-Ramirez, C.; Vorobyov, I.; MacKerell, A.D., Jr.; Pastor, R.W. Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types. J. Phys. Chem. B 2010, 114, 7830–7843. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Thiessen, P.A.; Bolton, E.E.; Chen, J.; Fu, G.; Gindulyte, A.; Han, L.; He, J.; He, S.; Shoemaker, B.A. PubChem substance and compound databases. Nucleic Acids Res. 2016, 44, D1202–D1213. [Google Scholar] [CrossRef] [PubMed]
- Cheng, T.; Zhao, Y.; Li, X.; Lin, F.; Xu, Y.; Zhang, X.; Li, Y.; Wang, R.; Lai, L. Computation of octanol-water partition coefficients by guiding an additive model with knowledge. J. Chem. Inf. Model. 2007, 47, 2140–2148. [Google Scholar] [CrossRef] [PubMed]
- Missner, A.; Pohl, P. 110 years of the Meyer–Overton rule: Predicting membrane permeability of gases and other small compounds. ChemPhysChem 2009, 10, 1405–1414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhargava, P.; Grover, A.; Nigam, N.; Kaul, A.; Ishida, Y.; Kakuta, H.; Kaul, S.C.; Terao, K.; Wadhwa, R. Anticancer activity of the supercritical extract of Brazilian green propolis and its active component, artepillin C: Bioinformatics and experimental analyses of its mechanisms of action. Int. J. Oncol. 2018, 52, 925–932. [Google Scholar] [CrossRef]
- Li, J.; Shen, Z.; Ma, X.; Ren, W.; Xiang, L.; Gong, A.; Xia, T.; Guo, J.; Wu, A. Neuropeptide Y Y1 receptors meditate targeted delivery of anticancer drug with encapsulated nanoparticles to breast cancer cells with high selectivity and its potential for breast cancer therapy. ACS Appl. Mater. Interfaces 2015, 7, 5574–5582. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.B.; Lee, R.J. Tumor-selective targeted delivery of genes and antisense oligodeoxyribonucleotides via the folate receptor. Adv. Drug Deliv. Rev. 2004, 56, 1193–1204. [Google Scholar] [CrossRef] [PubMed]
- Mahmoodzadeh, F.; Jannat, B.; Ghorbani, M. Chitosan-based nanomicelle as a novel platform for targeted delivery of methotrexate. Int. J. Biol. Macromol. 2019, 126, 517–524. [Google Scholar] [CrossRef]
- Chatzisideri, T.; Leonidis, G.; Sarli, V. Cancer-targeted delivery systems based on peptides. Future Med. Chem. 2018, 10, 2201–2226. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Zhang, M.; Yung, B.; Li, H.; Zhou, C.; Lee, L.J.; Lee, R.J. Lactosylated liposomes for targeted delivery of doxorubicin to hepatocellular carcinoma. Int. J. Nanomed. 2012, 7, 5465. [Google Scholar] [CrossRef] [Green Version]
- Ayatollahi, S.; Salmasi, Z.; Hashemi, M.; Askarian, S.; Oskuee, R.K.; Abnous, K.; Ramezani, M. Aptamer-targeted delivery of Bcl-xL shRNA using alkyl modified PAMAM dendrimers into lung cancer cells. Int. J. Biochem. Cell Biol. 2017, 92, 210–217. [Google Scholar] [CrossRef] [PubMed]







| Membrane | No. of POPC Molecules | No. of POPS Molecules | ||
|---|---|---|---|---|
| Outer Leaflet | Inner Leaflet | Outer Leaflet | Inner Leaflet | |
| Normal | 36 | 12 | 0 | 24 |
| Cancer | 24 | 24 | 12 | 12 |
| Cancer Cell Membrane | Normal Cell Membrane | XLOGP3-AA | |||
|---|---|---|---|---|---|
| P (cm/s) | log P | P (cm/s) | log P | ||
| Withanone (Wi-N) | 7.64 × 10−6 | −5.12 | 1.33 × 10−6 | −5.88 | 3.1 |
| Withaferin A (Wi-A) | 1.16 × 10−3 | −2.94 | 1.06 × 10−4 | −3.98 | 3.8 |
| Caffeic Acid Phenethyl Ester (CAPE) | 8.37 × 10−1 | −0.08 | 2.31 × 10−1 | −0.64 | 4.2 |
| Artepillin C (ARC) | 4.67 | 0.67 | 4.14 | 0.62 | 5.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radhakrishnan, N.; Kaul, S.C.; Wadhwa, R.; Sundar, D. Phosphatidylserine Exposed Lipid Bilayer Models for Understanding Cancer Cell Selectivity of Natural Compounds: A Molecular Dynamics Simulation Study. Membranes 2022, 12, 64. https://doi.org/10.3390/membranes12010064
Radhakrishnan N, Kaul SC, Wadhwa R, Sundar D. Phosphatidylserine Exposed Lipid Bilayer Models for Understanding Cancer Cell Selectivity of Natural Compounds: A Molecular Dynamics Simulation Study. Membranes. 2022; 12(1):64. https://doi.org/10.3390/membranes12010064
Chicago/Turabian StyleRadhakrishnan, Navaneethan, Sunil C. Kaul, Renu Wadhwa, and Durai Sundar. 2022. "Phosphatidylserine Exposed Lipid Bilayer Models for Understanding Cancer Cell Selectivity of Natural Compounds: A Molecular Dynamics Simulation Study" Membranes 12, no. 1: 64. https://doi.org/10.3390/membranes12010064
APA StyleRadhakrishnan, N., Kaul, S. C., Wadhwa, R., & Sundar, D. (2022). Phosphatidylserine Exposed Lipid Bilayer Models for Understanding Cancer Cell Selectivity of Natural Compounds: A Molecular Dynamics Simulation Study. Membranes, 12(1), 64. https://doi.org/10.3390/membranes12010064