Simulation and Experiment of Compression Molding Behavior of Substrate Block Suitable for Mechanical Transplanting Based on Discrete Element Method (DEM)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Determination of the Intrinsic Parameters of the Peat
2.1.1. Moisture Content and Density
2.1.2. Stacking Angle
2.2. Calibration of Discrete Element Simulation Parameters of the Peat
2.2.1. Setting of the Simulations
2.2.2. The Sensitivity of the DEM Parameters to the Stacking Angle
2.2.3. Calibration of DEM Parameters of Peat
2.3. DEM Simulation for the Compression Molding of Peat Substrate Blocks
2.4. Experiment on the Compression Molding of Peat Substrate Blocks
3. Results and Discussion
3.1. Calibration of the DEM Parameters of Peat
3.1.1. Plackett–Burman (PB) Test
3.1.2. The Steepest Climbing Test
3.1.3. Box–Behnken Test
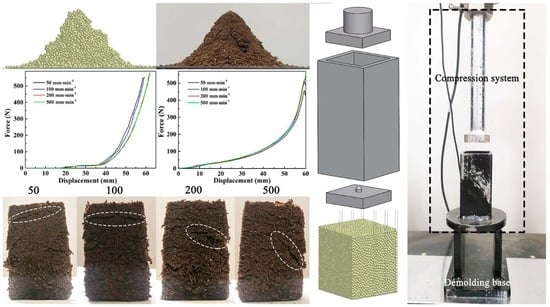
3.2. Compression Molding Behavior of Substrate Block
4. Conclusions
- (1)
- In the proposed calibration method of the DEM parameters of peat particles, the shear modulus of the particles, the static friction coefficient of the particle–particle interactions, the rolling friction coefficient of the particle-particle interactions, and surface energy were found have significant effects on the stacking angle of peat through the Plackett–Burman test. After the range was narrowed by the steepest climbing test, the significant parameters were optimized by the second-order regression model established in the Box–Behnken test. The result of the validation test of the stacking angle of peat under optimal parameters showed the average relative error between the simulated (50.89°) and the physical stacking angle (51.15°) was 0.51%, indicating the good reliability and accuracy of the DEM model and the simulated parameters of the peat particles.
- (2)
- In the physical and simulated experiments of the compression molding of peat substrate blocks, the compression force of the measured and simulated test all included an initial linear stage followed by a second non-linear stiffening stage in the whole compression process. Additionally, the maximum force increased with increasing loading speed in both the measured and simulated test. The relative errors between measured and simulated maximum force were around 10%, and, especially, the loading speed at 500 mm·min−1 was 5.45%. In general, the DEM simulations had a good match with the experimental measurements, and the DEM model could capture the compression behavior of particles.
- (3)
- The peat substrate blocks all exhibited surface cracks under different loading speeds, and the location of the crack was closer to the bottom as the loading speed increased. It was due to the inhomogeneous particle distribution, resulting in varying degrees of compaction along the forming direction at higher loading speeds. While the practical production of substrate blocks mostly involves rapid prototyping to ensure operational efficiency, the compression molding of pure peat usually has lower mechanical properties that do not meet the requirements of mechanical transplanting. Hence, it is suggested to add some agglomerant to enhance the interparticle binding.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Jin, X.; Tang, L.; Li, R.; Zhao, B.; Ji, J.; Ma, Y. Edge recognition and reduced transplantation loss of leafy vegetable seedlings with Intel RealsSense D415 depth camera. Comput. Electron. Agric. 2022, 198, 107030. [Google Scholar] [CrossRef]
- Nandede, B.M.; Carpenter, G.; Byale, N.A.; Chilur, R.; Jadhav, M.L.; Pagare, V. Manually operated single row vegetable transplanter for vegetable seedlings. Int. J. Agric. Sci. 2017, 9, 4911–4914. [Google Scholar]
- Rahul, K.; Raheman, H.; Paradkar, V. Design and development of a 5R 2DOF parallel robot arm for handling paper pot seedlings in a vegetable transplanter. Comput. Electron. Agric. 2019, 166, 105014. [Google Scholar] [CrossRef]
- Zhao, W.; Cui, Z.; Guan, C.; Chen, Y.; Yang, Y.; Gao, Q. Design and experiment of vegetable seedling substrate block forming machine. J. Chin. Agric. Mech. 2021, 42, 77–82. [Google Scholar]
- Gao, G.; Liang, Y.; Du, Y.; Zhao, W. Optimization design and test of compression molding mechanism. J. Chin. Agric. Mech. 2020, 41, 43–49. [Google Scholar]
- Xu, T.; Cui, Z.; Guan, C.; Chen, Y.; Xiao, T. Design and experiment of sending and taking seedling device of substrate block seedling transplanter. J. Chin. Agric. Mech. 2021, 42, 50–55. [Google Scholar]
- Yang, L.; Cao, H.; Yuan, Q.; Luoa, S.; Liu, Z. Component optimization of dairy manure vermicompost, straw, and peat in seedling compressed substrates using simplex-centroid design. J. Air Waste Manag. 2018, 68, 215–226. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, L.; Yuan, Q.; Liu, Z.; Cao, H.; Luo, S. Experiment on seedling of compressed substrates with cow dung aerobic composting and earthworm cow dung composting. Trans. Chin. Soc. Agric. Eng. 2016, 32, 226–233. [Google Scholar]
- Xin, M.; Chen, T.; Zhang, Q.; Jiao, J.; Bai, X.; Song, Y.; Zhao, R.; Wei, C. Parameters optimization for molding of vegetable seedling substrate nursery block with rice straw. Trans. Chin. Soc. Agric. Eng. 2017, 33, 219–225. [Google Scholar]
- Qu, P.; Cao, Y.; Wu, G.; Tang, Y.; Xia, L. Preparation and Properties of Coir-Based Substrate Bonded by Modified Urea Formaldehyde Resins for Seedlings. BioResources 2018, 13, 4332–4345. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Liu, D.; Xie, F.; Ashwehmbom, L.G.; Zhang, Z.; Tang, Q. Calibration of discrete element parameters and experimental verification for modelling subsurface soils. Biosyst. Eng. 2021, 212, 215–227. [Google Scholar] [CrossRef]
- Liu, K.; Su, H.; Li, F.; Jiao, W. Research on parameter calibration of soil discrete element model based on response surface method. J. Chin. Agric. Mech. 2021, 42, 143–149. [Google Scholar]
- Hoshishima, C.; Ohsaki, S.; Nakamura, H.; Watano, S. Parameter calibration of discrete element method modelling for cohesive and non-spherical particles of powder. Powder Technol. 2021, 386, 199–208. [Google Scholar] [CrossRef]
- Wan, D.; Wang, M.; Zhu, Z.; Wang, F.; Zhou, L.; Liu, R.; Gao, W.; Shu, Y.; Xiao, H. Coupled GIMP and CPDI material point method in modelling blast-induced three-dimensional rock fracture. Int. J. Min. Sci. Technol. 2022, 32, 1097–1114. [Google Scholar] [CrossRef]
- Luo, S. Molding Process and Molding Machine Design and Experiment of Vermicompost Substrate. Ph.D. Thesis, Huazhong Agricultural University, Wuhan, China, 2019. [Google Scholar]
- Zhao, L.; Zhou, H.; Xu, L.; Song, S.; Zhang, C.; Yu, Q. Parameter calibration of coconut bran substrate simulation model based on discrete element and response surface methodology. Powder Technol. 2022, 395, 183–194. [Google Scholar] [CrossRef]
- Xing, J.; Zhang, R.; Wu, P.; Zhang, X.; Dong, X.; Chen, Y.; Ru, S. Parameter calibration of discrete element simulation model for latosol particles in hot areas of Hainan Province. Trans. Chin. Soc. Agric. Eng. 2020, 36, 158–166. [Google Scholar]
- Liu, H.; Zhang, W.; Ji, Y.; Qi, B.; Li, K. Parameter calibration of soil particles in annual rice-wheat region based on discrete element method. J. Chin. Agric. Mech. 2020, 41, 153–159. [Google Scholar]
- Xia, R.; Li, B.; Wang, X.; Li, T.; Yang, Z. Measurement and calibration of the discrete element parameters of wet bulk coal. Measurement 2019, 142, 84–95. [Google Scholar] [CrossRef]
- Maraldi, M.; Molari, L.; Regazzi, N.; Molari, G. Analysis of the parameters affecting the mechanical behaviour of straw bales under compression. Biosyst. Eng. 2017, 160, 179–193. [Google Scholar] [CrossRef]







| Symbol | Parameters | Low Level (−1) | High Level (+1) |
|---|---|---|---|
| A | Poisson’s ratio of the particles | 0.2 | 0.4 |
| B | Shear modulus of the particles (MPa) | 1 | 10 |
| C | Impact recovery coefficient of particle–particle | 0.2 | 0.6 |
| D | Static friction coefficient of particle–particle | 0.2 | 0.8 |
| E | Rolling friction coefficient of particle–particle | 0.1 | 0.5 |
| F | Impact recovery coefficient of particle–steel | 0.2 | 0.6 |
| G | Static friction coefficient of particle–steel | 0.2 | 0.6 |
| H | Rolling friction coefficient of particle–steel | 0.05 | 0.25 |
| J | Surface energy (J·m−2) | 0.1 | 1 |
| K, L | Virtual parameter | −1 | 1 |
| Run | A | B | C | D | E | F | G | H | J | K | L | Stacking Angle (°) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | 59 |
| 2 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 32.76 |
| 3 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | 41.43 |
| 4 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | 57.17 |
| 5 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 33.38 |
| 6 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | 46.23 |
| 7 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 37.47 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 61.64 |
| 9 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 44.28 |
| 10 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | 54.66 |
| 11 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 84.23 |
| 12 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 83.65 |
| 13 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 43.13 |
| p | Contribution (%) | p-Value | Order |
|---|---|---|---|
| A | 3.05 | 0.0822 | 6 |
| B | 21.02 | 0.0133 * | 2 |
| C | 3.05 | 0.0821 | 5 |
| D | 18.56 | 0.0150 * | 3 |
| E | 5.17 | 0.0509 | 4 |
| F | 1.42 | 0.1549 | 9 |
| G | 1.85 | 0.1253 | 8 |
| H | 1.88 | 0.1236 | 7 |
| J | 43.42 | 0.0065 ** | 1 |
| No. | B | D | E | J | Stacking Angle (°) | Relative Error (%) |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.8 | 0.5 | 0.1 | 32.74 | 35.99 |
| 2 | 3.25 | 0.65 | 0.4 | 0.325 | 51.07 | 0.16 |
| 3 | 5.5 | 0.5 | 0.3 | 0.55 | 54.81 | 7.16 |
| 4 | 7.75 | 0.35 | 0.2 | 0.775 | 70.67 | 38.16 |
| 5 | 10 | 0.2 | 0.1 | 1 | 82.75 | 61.78 |
| Run | B | D | E | J | Stacking Angle (°) |
|---|---|---|---|---|---|
| 1 | 0 | 1 | −1 | 0 | 53.0542 |
| 2 | 0 | −1 | 1 | 0 | 56.04395 |
| 3 | 0 | 1 | 0 | 1 | 50.8817 |
| 4 | 1 | −1 | 0 | 0 | 55.8771 |
| 5 | 1 | 0 | −1 | 0 | 61.63415 |
| 6 | 0 | −1 | 0 | −1 | 46.189 |
| 7 | 0 | 0 | 0 | 0 | 53.98465 |
| 8 | 0 | 0 | 0 | 0 | 50.0464 |
| 9 | 0 | 0 | 0 | 0 | 53.55925 |
| 10 | 1 | 0 | 0 | −1 | 44.7601 |
| 11 | 0 | 0 | 0 | 0 | 53.65835 |
| 12 | 0 | 0 | −1 | −1 | 47.10265 |
| 13 | 0 | 1 | 0 | −1 | 41.7636 |
| 14 | −1 | 0 | 1 | 0 | 50.258 |
| 15 | −1 | 0 | 0 | −1 | 39.92395 |
| 16 | 0 | 0 | 1 | 1 | 62.2329 |
| 17 | 0 | −1 | 0 | 1 | 59.3303 |
| 18 | 0 | 0 | 1 | −1 | 44.90385 |
| 19 | 0 | 0 | −1 | 1 | 58.3123 |
| 20 | −1 | 0 | −1 | 0 | 55.354 |
| 21 | 1 | 0 | 1 | 0 | 58.5406 |
| 22 | −1 | 1 | 0 | 0 | 47.8322 |
| 23 | −1 | −1 | 0 | 0 | 51.86525 |
| 24 | −1 | 0 | 0 | 1 | 60.9074 |
| 25 | 1 | 1 | 0 | 0 | 56.82535 |
| 26 | 0 | −1 | −1 | 0 | 57.6126 |
| 27 | 1 | 0 | 0 | 1 | 54.70705 |
| 28 | 0 | 1 | 1 | 0 | 56.0758 |
| 29 | 0 | 0 | 0 | 0 | 56.5945 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 867.18 | 14 | 61.94 | 8.63 | 0.0001 ** |
| B | 57.22 | 1 | 57.22 | 7.98 | 0.0135 * |
| D | 34.97 | 1 | 34.97 | 4.87 | 0.0444 * |
| E | 2.10 | 1 | 2.10 | 0.2921 | 0.5974 |
| J | 556.63 | 1 | 556.63 | 77.58 | <0.0001 ** |
| BD | 6.20 | 1 | 6.20 | 0.8646 | 0.3682 |
| BE | 1.00 | 1 | 1.00 | 0.1397 | 0.7142 |
| BJ | 30.45 | 1 | 30.45 | 4.24 | 0.0585 |
| DE | 5.27 | 1 | 5.27 | 0.7342 | 0.4059 |
| DJ | 4.05 | 1 | 4.05 | 0.5640 | 0.4651 |
| EJ | 9.36 | 1 | 9.36 | 1.30 | 0.2725 |
| B2 | 0.0047 | 1 | 0.0047 | 0.0007 | 0.9800 |
| D2 | 2.45 | 1 | 2.45 | 0.3419 | 0.5680 |
| E2 | 52.94 | 1 | 52.94 | 7.38 | 0.0167 * |
| J2 | 75.29 | 1 | 75.29 | 10.49 | 0.0059 ** |
| Residual | 100.44 | 14 | 7.17 | ||
| Lack of fit | 78.70 | 10 | 7.87 | 1.45 | 0.3851 |
| Pure error | 21.74 | 4 | 5.44 | ||
| Cor Total | 967.62 | 28 |
| Loading Speed (mm·min−1) | Maximum Compressive Force (N) | Relative Error (%) | |
|---|---|---|---|
| Measured | Simulated | ||
| 50 | 456.2 | 520.9 | 14.18 |
| 100 | 509.6 | 550.9 | 8.10 |
| 200 | 526.6 | 573.0 | 8.81 |
| 500 | 550.8 | 580.8 | 5.45 |
| Loading Speed (mm·min−1) | Particle Number | Average Particle Number | Variable Coefficient (%) | ||
|---|---|---|---|---|---|
| Center | Quarter | Side | |||
| 50 | 827 | 861 | 690 | 793 (90.52) | 11.42 |
| 100 | 836 | 848 | 691 | 792 (87.39) | 11.04 |
| 200 | 823 | 836 | 660 | 773 (98.08) | 12.69 |
| 500 | 814 | 841 | 655 | 770 (100.50) | 13.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, J.; Cui, Z.; Chen, Y.; Guan, C.; Chen, M.; Ma, B. Simulation and Experiment of Compression Molding Behavior of Substrate Block Suitable for Mechanical Transplanting Based on Discrete Element Method (DEM). Agriculture 2023, 13, 883. https://doi.org/10.3390/agriculture13040883
Fu J, Cui Z, Chen Y, Guan C, Chen M, Ma B. Simulation and Experiment of Compression Molding Behavior of Substrate Block Suitable for Mechanical Transplanting Based on Discrete Element Method (DEM). Agriculture. 2023; 13(4):883. https://doi.org/10.3390/agriculture13040883
Chicago/Turabian StyleFu, Jingjing, Zhichao Cui, Yongsheng Chen, Chunsong Guan, Mingjiang Chen, and Biao Ma. 2023. "Simulation and Experiment of Compression Molding Behavior of Substrate Block Suitable for Mechanical Transplanting Based on Discrete Element Method (DEM)" Agriculture 13, no. 4: 883. https://doi.org/10.3390/agriculture13040883
APA StyleFu, J., Cui, Z., Chen, Y., Guan, C., Chen, M., & Ma, B. (2023). Simulation and Experiment of Compression Molding Behavior of Substrate Block Suitable for Mechanical Transplanting Based on Discrete Element Method (DEM). Agriculture, 13(4), 883. https://doi.org/10.3390/agriculture13040883