Significance of Fluvial Sediment Supply in Coastline Modelling at Tidal Inlets

Abstract

The sediment budget associated with future coastline change in the vicinity of tidal inlets consists of four components; sea level rise-driven landward movement of the coastline (i.e., the Bruun effect), basin infilling effect due to sea level rise-induced increase in accommodation space, basin volume change due to variation in river discharge, and coastline change caused by change in fluvial sediment supply. These four components are affected by climate change and/or anthropogenic impacts. Despite this understanding, holistic modelling techniques that account for all the aforementioned processes under both climate change and anthropogenic influences are lacking. This manuscript presents the applications of a newly-developed reduced complexity modelling approach that accounts for both climate change and anthropogenically-driven impacts on future coastline changes. Modelled results corresponding to the year 2100 indicate considerable coastline recessions at Wilson Inlet (152 m) and the Swan River system (168 m) in Australia and Tu Hien Inlet (305 m) and Thuan An Inlet (148 m) in Vietnam. These results demonstrate that coastline models should incorporate both climate change and anthropogenic impacts to quantify future changes in fluvial sediment supply to coasts to achieve better estimates of total coastline changes at tidal inlets. Omission of these impacts is one of the major drawbacks in all the existing coastline models that simulate future coastline changes at tidal inlets. A comparison of these modelled future coastline changes with the predictions made by a relevant existing modelling technique (Scale Aggregated Model for Inlet-interrupted Coasts (SMIC)) indicates that the latter method overestimates total coastline recessions at the Swan River system, and the Tu Hien and Thuan An Inlets by 7%, 10%, and 30%, respectively, underlining the significance of integrating both climate change and anthropogenic impacts to assess future coastline changes at tidal inlets.

1. Introduction

Coastlines in the vicinity of tidal inlets are shaped and affected not only by oceanic processes like tides, waves and mean sea level changes, but also by terrestrial processes, such as river flow, fluvial sediment supply, land use pattern changes, and land management [1,2,3]. For a given combination of anthropogenic impacts, such as deforestation, damming of rivers, and changes in land use and management patterns and environmental forcing, like rainfall and temperature, a river catchment will produce a certain amount of sediment flux. Depending on river morphodynamics, all or part of this sediment will eventually enter the downstream estuary. Depending on whether the estuary is in a sediment importing or exporting phase (relative to the ocean side of the estuary), all or part of the fluvial sediment received by the estuary will either settle within the estuary or enter the nearshore zone. Subjected to contemporary wave and tide processes, sediment supplied into the nearshore zone may contribute to one or more morphodynamic processes (e.g., ebb-delta development, coastline progradation, deposition on the lower shoreface). Any substantial change(s) in anthropogenic impact(s), such as dam construction or demolition, changes in crop patterns, changes in land management or variation(s) in environmental forcing due to climate change, could result in considerable changes in these sediment transport pathways. This could, in turn, have significant implications on estuary morphology, tidal flats, wetlands, coastlines, ebb-deltas, shorefaces, and a myriad of other physical impacts.

Despite scientists, engineers and managers having been, for decades, cognisant of this fact, owing to the inherent divisions between traditional academic disciplines such as hydrology, geology, oceanography, and coastal engineering, have resulted in a fragmented approach towards assessing anthropogenic and climate change driven impacts on long-term evolution of catchment, estuarine, and coastal systems. Owing to this reason, most of the studies to date have concentrated only on one or two of the three main components of catchment-estuary-coastal systems (CEC systems), while ignoring the other(s) (e.g., [2,3,4,5,6,7]). Given that the foreshadowed population growth and predicted climate change by the 21st century and beyond, suitable modelling techniques that can effectively simulate the long-term evolution of catchment, estuarine and coastal system behaviour are (urgently) required by contemporary coastal zone planners and managers to investigate the probable impacts of the aforementioned system forcing on the holistic behaviour of CEC systems.

The Scale-aggregated Model for Inlet-interrupted Coasts (SMIC) presented by [8] is the first of its kind that treats CEC systems in a holistic manner, while giving consideration to the description of physics governing each of the three components of the integrated systems. Although SMIC provides a solid platform to holistically probe into CEC systems, the highly-simplified method adopted in quantifying the fluvial sediment supply can be identified as its major drawback in accurately estimating the long-term behaviour of CEC systems under climate change and anthropogenic forcing.

Given the vulnerabilities of estuary-coastal systems, their significance and laps in existing modelling techniques that can holistically simulate their future behaviour, a reduced complexity modelling (RC modelling) technique is currently being developed to assess probable local scale (~30 km alongshore) coastline changes in the vicinity of small tidal inlets, estuaries with low-lying margins and barrier island coasts at macro (50–100 year) time scales. This manuscript presents a part of this study, which scrutinizes the significance of fluvial sediment supply in assessing future coastlines changes at small tidal inlets. Case studies used in SMIC applications [8] were used in this work as well, making it convenient to compare this model performances with that of relevant existing method(s). Therefore, this study focuses on coastline variations at CEC systems in Western Australia (Wilson Inlet and Swan River) and Vietnam (Tu Hien and Thuan An Inlets). Inlet-estuary systems considered in this study are small barrier estuaries, which can be found along microtidal, wave-dominated sandy coasts (~50% of the world’s coastlines [9]). These four sites represent seasonally (Wilson), intermittently (Tu Hien), and permanently open (Swan River and Thuan An) inlet systems. They are also attributed with different basin and tidal prisms sizes and annual river flow volumes [8]. Compared to the present conditions, the catchments of Tu Hien and Thuan An inlet systems would generate larger river discharge volumes by 2100, whereas these volumes from the Wilson and Swan river systems are expected to be smaller [10].

2. Methods

Total coastline change at a tidal inlet can be synthesized according to the following [8]:

$$\Delta {\mathrm{C}}_{\mathrm{T}}=\Delta {\mathrm{C}}_{\mathrm{BE}}+\Delta {\mathrm{C}}_{\mathrm{BI}}+\Delta {\mathrm{C}}_{\mathrm{BV}}+\Delta {\mathrm{C}}_{\mathrm{FS}}$$

(1)

where $\Delta {\mathrm{C}}_{\mathrm{T}}$ is the total coastline change (m), $\Delta {\mathrm{C}}_{\mathrm{BE}}$ is sea-level rise driven landward movement of the coastline, $\Delta {\mathrm{C}}_{\mathrm{BI}}$ is the basin infilling due to sea-level rise induced increase in accommodation space, $\Delta {\mathrm{C}}_{\mathrm{BV}}$ is the basin volume change due to variation in river flow and $\Delta {\mathrm{C}}_{\mathrm{FS}}$ is the coastline change due to change in the fluvial sediment supply.

For detailed insights regarding the derivations of above four components in equation [1], readers are referred to [8]. Given the focal point of this study hinges on the significance of fluvial sediment supply in assessing future coastline changes, brief descriptions of the relevant methods adopted are presented herewith.

2.1. Sea-Level Rise-Driven Landward Movement of the Coastline

Conceivably the most renowned climate-change driven impact on coastlines, described by [11]. The resulting coastline recession ($\Delta {\mathrm{C}}_{\mathrm{BE}}$) is given by:

$$\Delta {\mathrm{C}}_{\mathrm{BE}}=\frac{\Delta \mathrm{S}}{\tan \mathsf{\beta }}$$

(2)

where ${\mathsf{\Delta }\mathrm{C}}_{\mathrm{BE}}$ is the coastal recession (m), $\mathsf{\Delta }\mathrm{S}$ is sea level rise (m), and $\mathsf{\beta }$ is the slope of the active beach profile.

2.2. Basin Infilling due to Sea-Level Rise-Induced Increase in Accommodation Space

Accommodation space is the additional volume created within the basin due to a given increment in mean sea-level $\left(\Delta \mathrm{S}\right)$. This volume ($\Delta \mathrm{S}\times {\mathrm{A}}_{\mathrm{b}}$; where, ${\mathrm{A}}_{\mathrm{b}}$ is the basin surface area (${\mathrm{m}}^2$)) results in a sediment demand that creates an additional coastline erosion ($\Delta {\mathrm{C}}_{\mathrm{BI}}$ (m)). Such a coastal recession results in a landward shift of the coastal profile from the coastline to the depth of closure (${\mathrm{h}}_{\mathrm{DoC}}$ (m)) along a certain alongshore length (affected coastline length (${\mathrm{L}}_{\mathrm{AC}}$ (m))).

There exists a timescale difference in sea-level rise (hydrodynamic forcing) and concomitant basin infilling (morphological response). This lag in morphological response is estimated to be about 50% of the volume required by the corresponding forcing conditions [8]. These relationships can be expressed as the following:

$$\Delta {\mathrm{C}}_{\mathrm{BI}}\times {\mathrm{L}}_{\mathrm{AC}}\times {\mathrm{h}}_{\mathrm{DoC}}=\mathrm{fac}\times \Delta \mathrm{S}\times {\mathrm{A}}_{\mathrm{b}}$$

(3)

2.3. Basin Volume Change due to Variation in River Flow

Basin volume would change due to the possible future changes in annual river discharge ($\Delta {\mathrm{Q}}_{\mathrm{R}}$ (${\mathrm{m}}^3$)). In order to maintain the basin cross-sectional velocities, a basin-inlet system would undergo changes in its bed level, so that the changes in basin volume is accommodated. This process will result in a certain change in the nearby coast (${\mathsf{\Delta }\mathrm{C}}_{\mathrm{BV}}\left(\mathrm{m}\right)$), which can be calculated as the following [8]:

$$\Delta {\mathrm{C}}_{\mathrm{BV}}\times {\mathrm{L}}_{\mathrm{AC}}\times {\mathrm{h}}_{\mathrm{DoC}}=\frac{\Delta {\mathrm{Q}}_{\mathrm{R}}\times {\mathrm{V}}_{\mathrm{B}}}{\left(\mathrm{P}+{\mathrm{Q}}_{\mathrm{R}}\right)}$$

(4)

where ${\mathrm{Q}}_{\mathrm{R}}$ is the present river flow into the basin during ebb (${\mathrm{m}}^3$), $\Delta {\mathrm{Q}}_{\mathrm{R}}$ is the climate-change driven variation in river flow during ebb (${\mathrm{m}}^3$), ${\mathrm{V}}_{\mathrm{B}}$ is the present basin volume (${\mathrm{m}}^3$) and P is the mean ebb tidal prism (${\mathrm{m}}^3$).

2.4. Coastline Change due to Changes in Fluvial Sediment Supply

Anthropogenic and climate-change driven impacts that may occur in future would result in swift changes in fluvial sediment ($\Delta {\mathrm{Q}}_{\mathrm{S}}\mathrm{in}{\mathrm{m}}^3$) supplied to coasts. Subsequently, these changes would affect the volume of sediment exchanged between the basin and its neighbouring coast. The relevant changes in coastline ($\Delta {\mathrm{C}}_{\mathrm{FS}}$ (m)) can be calculated as [8]:

$$\Delta {\mathrm{C}}_{\mathrm{FS}}\times {\mathrm{L}}_{\mathrm{AC}}\times {\mathrm{h}}_{\mathrm{DoC}}={{\displaystyle \int }}_0^{\mathrm{T}}\Delta {\mathrm{Q}}_{\mathrm{S}}\left(\mathrm{t}\right)·\mathrm{dt}$$

(5)

where T is the time period considered (in years).

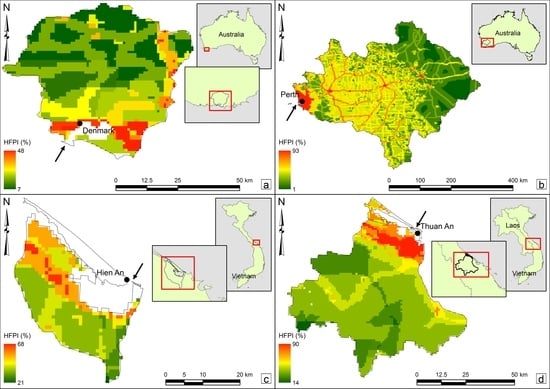
2.5. Factors Affecting Fluvial Sediment Supply to Coasts

Rivers contribute for about 95% of the sediment received by the oceans [12]. Despite the amount of soil eroded from catchments is increasing due to the combined effects of climate change and anthropogenic impacts [12,13,14], it is being reported that the amount of sediment received by the oceans is considerably reduced caused by anthropogenic sediment retention [3,7,12,15]. Therefore, it is generally accepted that anthropogenic factors overwhelm the impact of natural processes on fluvial sediment supply to the coasts [15].

Climatic factors such as temperature, mean and extreme rainfall, and river flow are the main factors that affect fluvial sedimentation [12,13,16]. Predicted climate changes in the future would most likely result in an increased temperature [17], thus influencing the rate of soil erosion (both chemical and mechanical) and storage and the release of water from the Earth’s lithosphere [13]. The combined effect of reduced rainfall and increased temperature results in water stresses to plants, resulting in diminished growths and, hence, amplified soil erosion that results in a larger sediment yield from catchments. Contrariwise, high rainfall and low temperatures facilitate favourable conditions for plant growth, and hence reduce soil erosion, which in turn diminishes the sediment yield from catchments [16]. Global-scale studies indicate that the rivers contemporary discharge less water to the oceans due to both increased water usage and diminished precipitation [7,15,17,18,19], which, in turn, directly affects fluvial sediment supply to the coasts and oceans.

On the other hand, anthropogenic impacts on fluvial sediment supply vary over a wider spectrum. Land-use management practices (e.g., urbanization, changes in land use, land management and agricultural practices), changes in water management practices (e.g., dam constructions or demolition, streamflow regulation, introduction of flood control mechanisms) and river sand mining are the most prominent human-induced drivers that affect fluvial sediment supply [7,12,13,15,18]. Owing to the aforementioned factors, human activities have simultaneously increased catchment sediment yield via accelerated soil erosion, yet, have also significantly reduced the amount of sediment received by the coasts due to retention within reservoirs [3,7,13,15,16,20,21,22].

2.6. Assessment of Fluvial Sediment Supply to Coasts

The proposed new reduced complexity model by [23] utilizes the empirical BQART model presented by [13] to assess the annual fluvial sediment supply to the coasts. This empirical model is based on 488 globally-distributed datasets. For catchments with a mean annual temperature greater than or equal to 2 °C, the aforementioned model estimates annual sediment volume supplied to the coast by the following equation:

$${\mathrm{Q}}_{\mathrm{s}}=\mathsf{\omega }\times \mathrm{B}\times {\mathrm{Q}}^{0.31}\times {\mathrm{A}}^{0.5}\times \mathrm{R}\times \mathrm{T}$$

(6)

where ω is 0.02 or 0.0006 for the sediment volume $\left({\mathrm{Q}}_{\mathrm{s}}\right)$, expressed in kg/s or MT/year, respectively, Q is the annual river discharge from the catchment considered $\left({\mathrm{km}}^3/\mathrm{year}\right)$, A is the catchment area $\left({\mathrm{km}}^2\right)$, R is the relief of the catchment (km) and T is the catchment-wide mean annual temperature (℃).

Term ‘B’ in the above equation [6] represents the catchment sediment production and comprises glacial erosion $\left(\mathrm{I}\right)$, catchment lithology (L) that accounts for its soil type and erodibility, a reservoir trapping efficiency factor $\left({\mathrm{T}}_{\mathrm{E}}\right)$, and the human-induced erosion factor $\left({\mathrm{E}}_{\mathrm{h}}\right)$, which is expressed as follows:

$$\mathrm{B}=\mathrm{IL}\left(1-{\mathrm{T}}_{\mathrm{E}}\right){\mathrm{E}}_{\mathrm{h}}$$

(7)

Glacial erosion $\left(\mathrm{I}\right)$ in above equation [7] is expressed as:

$$\mathrm{I}=1+\left(0.09{\mathrm{A}}_{\mathrm{g}}\right)$$

(8)

where ${\mathrm{A}}_{\mathrm{g}}$ is the percentage of ice cover of the catchment area.

The human-induced erosion factor (${\mathrm{E}}_{\mathrm{h}}$; anthropogenic factor) of the above equation [7] depends on land-use practices, socio-economic conditions and population density [13]. The authors of [13] have estimated this human disturbance potential based on Gross National Product (per capita) and population density and have also suggested its optimum rage to between 0.3 and 2.0.

Instead of using countrywide estimates of GNP/capita and population density to estimate the human-induced soil erosion factor (${\mathrm{E}}_{\mathrm{h}}$), high-resolution spatial information published by [24] in the form of a human footprint index (HFPI) is used in this study, so that the anthropogenic influences on sedimentation is better represented [21,23]. The human footprint index is developed by using several global datasets such as population distribution, urban areas, roads, navigable rivers, electrical infrastructures and agricultural land use [25]. This dataset is available at a spatial resolution of 0.25 × 0.25 degrees and is regionally normalized to account for the interaction between the natural environment and human influences [25]. Figure 1 illustrates the human footprint indices across the catchments of the selected four case study sites. These HFPI values were used to determine the human-induced erosion factors for the respective catchment areas.

In the model presented by [8], future changes in fluvial sediment supply are calculated based on the Universal Soil Loss Equation (USLE):

$${\mathrm{A}}_{\mathrm{sl}}={\mathrm{R}}_{\mathrm{sl}}\times {\mathrm{K}}_{\mathrm{sl}}\times {\mathrm{L}}_{\mathrm{sl}}\times {\mathrm{S}}_{\mathrm{sl}}\times {\mathrm{C}}_{\mathrm{sl}}\times {\mathrm{P}}_{\mathrm{sl}}$$

(9)

where; ${\mathrm{A}}_{\mathrm{sl}}$ is the annual soil loss $\left({\mathrm{m}}^3\right)$ per unit area in the catchment, ${\mathrm{R}}_{\mathrm{sl}}$ is the rainfall erosivity factor, ${\mathrm{K}}_{\mathrm{sl}}$ is the soil erodibility factor, ${\mathrm{L}}_{\mathrm{sl}}$ is the slope length factor, ${\mathrm{S}}_{\mathrm{sl}}$ is the slope gradient factor, ${\mathrm{C}}_{\mathrm{sl}}$ is the crop/vegetation management factor and ${\mathrm{P}}_{\mathrm{sl}}$ is the support practice factor (all dimensionless).

Despite the fact that the USLE encapsulates both anthropogenic and climate-change driven impacts on fluvial sediment supply, in the Scaled Aggregated Model for Inlet-interrupted Coasts (SMIC), change in fluvial sediment supply is calculated only by considering the variations in annual rainfall from a present to future time horizon. This highly-simplified method adopted by [8] omits factors like changes in temperature, river discharge, land use, and land management practises, which can significantly influence the changes in future sediment supply to the coasts.

3. Model Applications and Results

The newly-developed reduced complexity model for small tidal inlets is applied at the selected four study sites to assess the potential coastline changes due to anthropogenic and climate change impacts by 2100. Model input parameters in

Table 1. Model input parameters (present conditions).

Parameter	Wilson Inlet	Swan River	Tu Hien Inlet	Thuan An Inlet
$\mathrm{River}\mathrm{discharge}\left(\mathrm{Q}\mathrm{in}{\mathrm{km}}^3/\mathrm{year}\right)$	0.2	0.5	0.8	5.5
$\mathrm{Temperature}\left(\mathrm{T}\mathrm{in}°\mathrm{C}\right)$	23	23	25	25
$\mathrm{Mean}\mathrm{ebb}\mathrm{tidal}\mathrm{prism}\left(\mathrm{P}\mathrm{in}{10}^6{\mathrm{m}}^3\right)$ *	2.4	2.6	15	47
$\mathrm{Basin}\mathrm{surface}\mathrm{area}\left({\mathrm{A}}_{\mathrm{b}}\mathrm{in}{\mathrm{km}}^2\right)$ *	48	52	100	110
$\mathrm{Basin}\mathrm{volume}\left({\mathrm{V}}_{\mathrm{b}}\mathrm{in}{10}^6{\mathrm{m}}^3\right)$ *	85	312	122	178
$\mathrm{Catchment}\mathrm{area}\left(\mathrm{A}\mathrm{in}{\mathrm{km}}^2\right)$ *	2263	121,000	600	3800
$\mathrm{Catchment}\mathrm{relief}\left(\mathrm{R}\mathrm{in}\mathrm{km}\right)$	0.16	0.53	1.2	1.2
$\mathrm{Lithology}\mathrm{factor}\left(\mathrm{L}\right)$ **	0.5	0.5	1.0	1.0
$\mathrm{Anthropogenic}\mathrm{factor}\left({\mathrm{E}}_{\mathrm{h}}\right)$	0.55	0.58	0.99	0.82
$\mathrm{Beach}\mathrm{profile}\mathrm{slope}\left(\tan \mathsf{\beta }\right)$ *	0.01	0.01	0.01	0.01
$\mathrm{Depth}\mathrm{of}\mathrm{closure}\left({\mathrm{h}}_{\mathrm{DoC}}\mathrm{in}\mathrm{m}\right)$ *	20	20	15	15
$\mathrm{Inlet}-\mathrm{affected}\mathrm{coastline}\mathrm{length}\left({\mathrm{L}}_{\mathrm{AC}}\mathrm{in}\mathrm{m}\right)$ *	15	20	10	20

* according to the values adopted in [8], ** obtained from [13].

are obtained from published literature or by using standard calculations. River discharge (Q) values are obtained from the Supplementary Table 1 of [8]. Annual mean temperature values (T) are calculated by utilizing relevant daily temperature values, obtained from the ERA 40 dataset that was published by The European Centre for Medium-Range Weather Forecasts (ECMWF). Anthropogenic factors on soil erosion at catchments $\left({\mathrm{E}}_{\mathrm{h}}\right)$ are represented via HFPI data, obtained from [24]. Those HFPI values were linearly rescaled to be complied with the optimum range (0.3, 2.0) suggested by [13] for human induced erosion factor $\left({\mathrm{E}}_{\mathrm{h}}\right)$.

Temperature projections of Representative Concentration Pathway 8.5 (RCP 8.5) were obtained from the 5th Assessment Report of the Intergovernmental Panel on Climate Change [17]. The authors of [8] have adopted 0.8 m of sea-level rise as one of the climate-change driven model input parameters. Therefore, in this study, the future increment of temperature $\left(\Delta \mathrm{T}\right)$ was selected to be the likely maximum increment predicted in [17]. Changes in future runoff $\left(\Delta \mathrm{Q}\right)$ are the percentage values adopted in [8], which are obtained from Figure 3.5 of [10]. Selecting the corresponding increment for the anthropogenic erosion factor $\left({\mathrm{E}}_{\mathrm{h}}\right)$ was mainly governed by the rate of population growth, urbanization, and proposed development plans within the study areas. Due to the large uncertainties associated with those aforementioned factors, one value was set for all the four sites considered in this study. Thus, the baseline case simulation input parameters presented in

Table 2. Model input parameters for baseline case simulation (year 2100).

Parameter	Wilson Inlet	Swan River	Tu Hien Inlet	Thuan An Inlet
$\mathrm{Sea}\mathrm{level}\mathrm{rise}\left(\Delta \mathrm{S}\mathrm{in}\mathrm{m}\right)$	0.8	0.8	0.8	0.8
$\mathrm{Temperature}\mathrm{increment}\left(\Delta \mathrm{T}\mathrm{in}°\mathrm{C}\right)$	4.8	4.8	4.8	4.8
$\mathrm{Change}\mathrm{in}\mathrm{run}\mathrm{off}\left(\Delta \mathrm{Q}\mathrm{in}\%\right)$	−30	−30	+15	+15
$\mathrm{Change}\mathrm{in}\mathrm{anthropogenic}\mathrm{factor} \left(\Delta {\mathrm{E}}_{\mathrm{h}}\mathrm{in}\%\right)$	+20	+20	+20	+20

consist of the worst-case climate change and anthropogenic forcing combinations.

Predicted coastline changes at the four study sites by 2100 are presented in

Table 3. Modelled coastline changes of the baseline case simulation.

Component	Potential Coastline Change (m) by 2100
	Wilson Inlet	Swan River	Tu Hien Inlet	Thuan An Inlet
$\mathrm{Bruun}\mathrm{effect}\left(\Delta {\mathrm{C}}_{\mathrm{BE}}\right)$	80	80	80	80
$\mathrm{Basin}\mathrm{Infilling}\mathrm{effect}\left(\Delta {\mathrm{C}}_{\mathrm{BI}}\right)$	64	52	266	146
$\mathrm{Basin}\mathrm{volume}\mathrm{change}\mathrm{effect}\left(\Delta {\mathrm{C}}_{\mathrm{BV}}\right)$	9	48	−4	−7
$\mathrm{Fluvial}\mathrm{sediment}\mathrm{supply}\mathrm{effect}\left(\Delta {\mathrm{C}}_{\mathrm{FS}}\right)$	−1	−12	−37	−71
$\mathrm{Total}\left(\Delta {\mathrm{C}}_{\mathrm{T}}\right)$	152	168	305	148

(herein, the baseline case simulation results). Positive and negative values in all the coastline changes are corresponding to coastline recession and progradation, respectively.

Above baseline case simulation results (Table 3) are compared with the modelled outcomes published by [8]. Since three of the four components (Bruun effect $\left(\Delta {\mathrm{C}}_{\mathrm{BE}}\right)$, Basin Infilling effect $\left(\Delta {\mathrm{C}}_{\mathrm{BI}}\right)$ and Basin volume change effect $\left(\Delta {\mathrm{C}}_{\mathrm{BV}}\right)$, highlighted in Table 3) of the total coastline change at tidal inlets are similar for both the models considered, only the relevant coastline changes due fluvial sediment supply variation and resulting total coastline changes by 2100 are presented in

Table 4. Comparison of predicted coastline changes with SMIC predictions.

Component		Potential Coastline Change (m) by 2100
		Wilson Inlet	Swan River	Tu Hien Inlet	Thuan An Inlet
$\mathrm{Fluvial}\mathrm{sediment}\mathrm{supply}\mathrm{effect}\left(\Delta {\mathrm{C}}_{\mathrm{FS}}\right)$	New RCM	−1	−12	−37	−71
	SMIC	0	0	−2	−7
$\mathrm{Total}\left(\Delta {\mathrm{C}}_{\mathrm{T}}\right)$	New RCM	152	168	305	148
	SMIC	153	180	340	212
Difference in Total [New RCM—SMIC]		−1 (~0%)	−12 (−7%)	−35 (−10%)	−64 (−30%)

RCM—Reduced Complexity Model.

.

In order to determine the sensitivity of climate change and anthropogenic forcing on fluvial sediment supply and subsequently their impacts on total coastline change at tidal inlets, different sets of model input parameters were also considered. For those model inputs, climate change projections relevant to the lower limits of the Representative Concentration Pathway 2.6 (RCP 2.6), presented in [17] were used. The corresponding value for anthropogenic impact was selected by considering the relentless population growth and myriad environmental pressures accompanied with it. These model input parameters, together with the relevant coastline changes are presented in

Table 5. Modelled coastline changes by 2100 under different climate-change and anthropogenic forcing scenarios considered.

Parameter	Component	Potential Coastline Change (m) by 2100
		Wilson Inlet	Swan River	Tu Hien Inlet	Thuan An Inlet
Baseline Simulation	$\mathrm{Total}\left(\Delta {\mathrm{C}}_{\mathrm{T}}\right)$	152	168	305	148
SMIC Results	$\mathrm{Total}\left(\Delta {\mathrm{C}}_{\mathrm{T}}\right)$	153	180	340	212
$\Delta \mathrm{T}=0.3°\mathrm{C}$	$\mathrm{FSS}\mathrm{effect}\left(\Delta {\mathrm{C}}_{\mathrm{FS}}\right)$	~0	−4	−21	−39
	$\mathrm{Total}\left(\Delta {\mathrm{C}}_{\mathrm{T}}\right)$	152	176	321	180
	% Difference from BLS	-	5%	5%	22%
$*\Delta \mathrm{Q}=\pm 5\%$	$\mathrm{FSS}\mathrm{effect}\left(\Delta {\mathrm{C}}_{\mathrm{FS}}\right)$	−1	−17	−34	−65
	$\mathrm{BVC}\mathrm{effect}\left(\Delta {\mathrm{C}}_{\mathrm{BV}}\right)$	1	8	−1	−2
	$\mathrm{Total}\left(\Delta {\mathrm{C}}_{\mathrm{T}}\right)$	144	123	311	159
	% Difference from BLS	−5%	−27%	2%	7%
$\Delta {\mathrm{E}}_{\mathrm{h}}=10\%$	$\mathrm{FSS}\mathrm{effect}\left(\Delta {\mathrm{C}}_{\mathrm{FS}}\right)$	~0	−8	−28	−53
	$\mathrm{Total}\left(\Delta {\mathrm{C}}_{\mathrm{T}}\right)$	152	172	314	166
	% Difference from BLS	-	2%	3%	12%

* Coastline changes at Wilson Inlet and Swan River (Australia) are driven by $\Delta \mathrm{Q}=-5\%$, whereas the same at Tu Hien and Thuan An Inlets (Vietnam) are driven by $\Delta \mathrm{Q}=+5\%$. FSS—Fluvial sediment supply, BVC—basin volume change, BLS—baseline simulation.

.

Model results under baseline case simulation indicate that the four tidal-affected coastlines considered in this study are significantly eroding due to the combined effects of climate change and anthropogenic impacts (Table 4). Two arid/semi-arid systems in the Australian continent, Wilson Inlet and Swan River systems, and the larger system in Vietnam, Thuan An Inlet, would experience coastal recessions of similar magnitudes (~150 m), whereas the smaller system in Vietnam, Tu Hien Inlet, shows a coastline retreat as double as that of the other three systems (~300 m). At all these systems, the Bruun effect $\left(\Delta {\mathrm{C}}_{\mathrm{BE}}\right)$ and basin infilling effect $\left(\Delta {\mathrm{C}}_{\mathrm{BI}}\right)$ (i.e., oceanic processes) are the main contributors for the resulting total coastline recessions (Table 3).

As a consequence of their arid climate, predicted coastline changes at the two systems in Australia are less affected by climate change-driven terrestrial processes. Furthermore, estimated anthropogenic impact factors for these two systems are also small. Therefore, the combined effects of climatic and anthropogenic forcing yield very little changes in fluvial sediment supply to these coasts, and, thus, result in minor changes at the two CEC systems in Australia. Tu Hien and Thuan An Inlets in Vietnam will pass more fluvial sediment to their nearshore zones due to the combined effects of climate change and anthropogenic forcing, resulting in considerable coastline progradation which, in turn, reduces the total coastal recessions caused by the two oceanic processes.

The lower extreme temperature increment and river discharge changes considered in Table 5 illustrate the relevance of different climate parameters on fluvial sediment supply and, subsequently, on total coastline changes at tidal inlets. Under the least temperature increment considered $\left(0.3 °\mathrm{C}\right)$, arid CEC systems in Australia show trivial coastline changes due to variations in fluvial sediment supply (~0 m and −4 m, respectively) by 2100. This is quite different for the two systems in Vietnam, where the coastline changes for the same climatic condition were recorded as −21 m and −39 m at Tu Hien and Thuan An Inlets, respectively. These effects on the coastline are considerably less than the baseline case simulation results of −37 m and −71 m calculated for the respective locations. Therefore, when compared with the baseline case simulation, the reduced temperature increment has resulted in about a 5% and 22% increase in total coastline recessions at Tu Hien and Thuan An Inlets, respectively.

Climate change-driven changes in river discharges have trivial impacts on total coastline changes in all of the systems. Reduced future river discharges in the Australian CEC systems (−5%) would increase the estuarine sediment demands, thus resulting in coastal recessions at Wilson Inlet (1 m) and Swan River systems (8 m). Under the baseline case simulation, coastal recessions due to basin volume changes at the same locations were recorded as 9 m and 48 m, respectively. Slightly increased river discharge predictions (+5%) in Vietnam by 2100 would result in trivial coastline progradations at Tu Hien Inlet (1 m) and Thuan An Inlet (2 m).

Possible future changes in waves and currents due to climate change may change sediment transport patterns at tidal inlets. However, investigating future changes in sediment transport patterns due to climate change driven variations in waves and currents is beyond the scope of this study. Hence, it is assumed that the existing sediment transport conditions at the inlets remain invariant over the time period considered in this study. Climate change is also likely to alter both intensity and frequency of storms. Such changes in storm conditions would cause irrevocable changes to the inlet-estuary systems and its adjacent coasts. The reduced complexity modelling techniques adopted in this study cannot represent such extreme events. System response to such events would be better represented via insights obtained from detailed process-based modelling techniques.

When the anthropogenic impact factor is set to be 10% greater than the present conditions, all the systems indicate coastline recessions by 2100. Tu Hien Inlet (9 m) and Thuan An Inlet (18 m) systems in Vietnam exhibit considerably increased total coastline recessions, while the same increment at Swan River system in Australia is predicted to be 4 m. Therefore, when compared with the baseline case simulation results, the reduced anthropogenic influence factor has accounted for about 2% increment in total coastline change in the Swan River system, whereas the same for Tu Hien and Thuan An Inlets are found to be about 3% and 12%, respectively.

4. Discussion

A comparison of the model results of the new reduced complexity model for small tidal inlets with SMIC outcomes exemplifies that the latter method tends to overestimate total coastal recession. This can be attributed to the differences in the methods adopted to estimate future fluvial sediment supply changes. In SMIC, the variation of future fluvial sediment supply is considered to be depend only on the percentage change in precipitation. Contrarily, in the new reduced complexity model, the same future variations are attributed to temperature, river discharge, and anthropogenic influences. Wilson Inlet in Australia is the only instance where the two methods have yielded similar predictions for total coastal recessions by 2100. Arid conditions and less anthropogenic impact within its catchment can be attributed as the main reasons for such an outcome. SMIC has overestimated the total coastal recessions in the Swan River system, and the Tu Hien and Thuan An Inlet systems by 12 m, 35 m, and 64 m, respectively. These overestimations are about 7%, 10%, and 30% of the total coastal recessions estimated by SMIC at the respective CEC systems (Table 4). Except for the arid Wilson Inlet system in Australia, SMIC results overestimate the predicted total coastline changes corresponding to the least increments of temperature, river discharge, and anthropogenic factors at other CEC systems as well (Table 5).

5. Conclusions

This manuscript presents a part of a long-term study that is being undertaken to investigate the holistic behaviour of catchment-estuary-coastal systems under the influences of both climate change and anthropogenic impacts at macro time scales. The corresponding new modelling technique for small tidal inlets was applied to four case study sites considered in a previous study to compare the performance of the new model with the existing method.

Model simulations indicate that the four systems considered in this study would experience significant coastal recessions by 2100. In all the four case study sites, climate-change induced sea-level rise-driven oceanic processes (i.e., the Bruun effect and the basin infilling effect) overwhelm the climate-change and anthropogenic impacts driven terrestrial processes (i.e., the basin volume effect and fluvial sediment supply effect). Except for the arid catchment conditions in the Wilson Inlet system, future changes in fluvial sedimentation would result in extra sediment supply to the coastal zones, reducing the total coastal recessions, especially at the Tu Hien and Thuan An Inlets in Vietnam by the next century. Therefore, accurate estimation of future changes in fluvial sediment supply is essential to determine the total coastline changes at tidal inlets.

A comparison of the baseline case simulation results with the modelled results for the lowest predictions for climate change impacts and anthropogenic factors by 2100 indicate that for non-arid conditions, temperature, river discharge, and human influences make significant impacts on fluvial sediment supply to coasts. Neglecting these terms would significantly undermine the assessment of future changes in the fluvial sediment supply to the coasts and, subsequently, the total coastline changes.

Despite being a comprehensive technique of assessing holistic behaviour of the catchment-estuary-coastal system at macro time scales, the Scale Aggregated Model for Inlet-interrupted Coasts (SMIC) does not account for anthropogenic impacts and also omits some key climatic parameters, such as temperature and river discharge, in assessing future changes in fluvial sediment supply to the coasts. Therefore, SMIC applications at small tidal inlet-estuary systems with sandy coasts and non-arid catchments are most likely to underpredict future changes in fluvial sediment supply to the coasts and, subsequently, overpredict coastline recession.