A Novel Obstacle Localization Method for an Underwater Robot Based on the Flow Field
Abstract
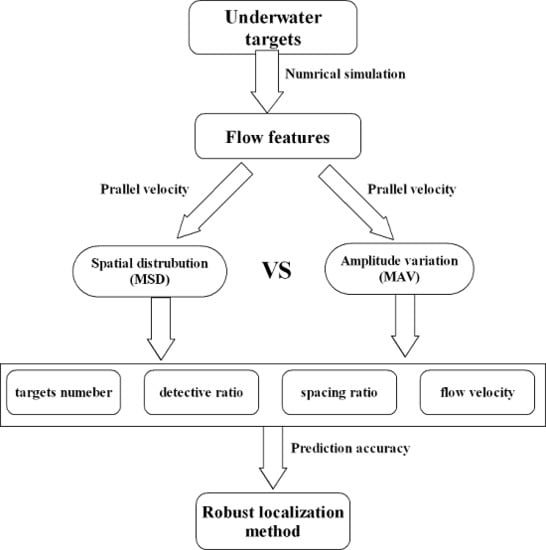
:1. Introduction
2. Implementation of the Test Problem
2.1. System Model
2.2. Numerical Method
2.3. Numerical Validation
3. Location Strategies
3.1. Method of Spatial Distribution (MSD)
3.2. Method of Amplitude Variation (MAV)
4. Discussion of Tandem Targets
4.1. Influence of the Spacing Ratio
4.2. Influence of the Flow Velocity
5. Conclusions
- The amplitude variation of extreme points on the parallel velocity curve can be used to estimate the locations of targets. For the cases of flow past one and two targets in a uniform flow field, the estimated error of MAV was less than 1%, which was evidently smaller than that of MSD.
- Changes in the detective ratio and spacing ratio had obvious influences on the estimated error of MSD, but they had little influence on the results of MAV.
- Robust flow sensing is not based on the spatial distribution of the flow field but rather, on the fluctuation range.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, J.H.; Kim, M.G.; Kang, H.; Lee, M.J.; Cho, G.R. UUV Simulation Modeling and its Control Method: Simulation and Experimental Studies. J. Mar. Sci. Eng. 2019, 7, 89. [Google Scholar] [CrossRef]
- Davide, C.; Marco, B.; Gabriele, B.; Massimo, C.; Andrea, R.; Enrica, Z.; Lucia, M.; Paola, C. A Novel Gesture-Based Language for Underwater Human-Robot Interaction. J. Mar. Sci. Eng. 2018, 6, 91. [Google Scholar]
- Corina, B.; Matthew, W.; Dunnigan, M.; Petillot, P. Coupled and Decoupled Force/Motion Controllers for an Underwater Vehicle-Manipulator System. J. Mar. Sci. Eng. 2018, 6, 96. [Google Scholar]
- Szyrowski, T.; Khan, A.; Pemberton, R.; Sharma, S.K.; Singh, Y.; Polvara, R. Range Extension for Electromagnetic Detection of Subsea Power and Telecommunication Cables. J. Mar. Sci. Eng. Technol. 2019, 1–8. [Google Scholar] [CrossRef]
- Emberton, S.; Chittka, L.; Cavallaro, A. Underwater Image and Video Dehazing with Pure Haze Region Segmentation. Comput. Vis. Image Underst. 2017, 168, 145–156. [Google Scholar] [CrossRef]
- Li, C.; Guo, J. Underwater Image Enhancement by Dehazing and Color Correction. J. Electron. Imaging 2015, 24, 033023. [Google Scholar] [CrossRef]
- Zhang, J.X. Principle of Biomimetic Detection Based on Flow Field Information of Underwater Moving Object. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2015. [Google Scholar]
- Muhammad, N.; Toming, G.; Tuhtan, J.A.; Musall, M.; Kruusmaa, M. Underwater Map-based Localization Using Flow Features. Auton. Robot. 2017, 41, 417–436. [Google Scholar] [CrossRef]
- Zheng, R.; Kamran, M. A Model of the Lateral Line of Fish for Vortex Sensing. Bioinspir. Biomim. 2012, 7, 036016. [Google Scholar]
- Coombs, S.; Patton, P. Lateral Line Stimulation Patterns and Prey Orienting Behavior in the Lake Michigan Mottled Sculpin (Cottus bairdi). J. Comput. Physiol. A 2009, 195, 279–297. [Google Scholar] [CrossRef]
- Mchenry, M.J.; Feitl, K.E.; Strother, J.A.; Trump, W.J.V. Larval Zebrafish Rapidly Sense the Water Flow of a Predator’s Strike. Biol. Lett. 2009, 5, 477–479. [Google Scholar] [CrossRef]
- Quinzio, S.; Fabrezi, M. The Lateral Line System in Anuran Tadpoles: Neuromast Morphology, Arrangement, and Innervation. Anat. Rec. 2014, 297, 1508–1522. [Google Scholar] [CrossRef] [PubMed]
- Schaumburg, F.; Kler, P.A.; Berli, C.L.A. Numerical Prototyping of Lateral Flow Biosensors. Sens. Actuators B Chem. 2018, 259, 1099–1107. [Google Scholar] [CrossRef]
- Tuhtan, J.A.; Fuentes-Pérez, J.F.; Strokina, N.; Toming, G.; Musall, M.; Noack, M.; Kruusmaa, M. Design and Application of a Fish-shaped Lateral Line Probe for Flow Measurement. Rev. Sci. Instrum. 2016, 87, 045110. [Google Scholar] [CrossRef] [PubMed]
- Dusek, J.E.; Triantafyllou, M.S.; Lang, J.H. Piezoresistive Foam Sensor Arrays for Marine Applications. Sens. Actuators A Phys. 2016, 248, 173–183. [Google Scholar] [CrossRef]
- Delamare, J.; Sanders, R.G.P.; Krijnen, G.J.M. 3D Printed Biomimetic Whisker-based Sensor with Co-planar Capacitive Sensing. In Proceedings of the 2016 IEEE International Conference on Sensors, Orlando, FL, USA, 30 October–3 November 2016. [Google Scholar]
- Zhu, P.; Ma, B.; Jiang, C.; Deng, J.; Wang, Y. Improved Sensitivity of Micro Thermal Sensor for Underwater Wall Shear Stress Measurement. Microsyst. Technol. 2015, 21, 785–789. [Google Scholar] [CrossRef]
- Djapic, V.; Dong, W.J.; Bulsara, A.; Anderson, G. Challenges in Underwater Navigation: Exploring Magnetic Sensors Anomaly Sensing and Navigation. In Proceedings of the 2016 IEEE International Conference on Sensors Applications Symposium, Zadar, Croatia, 13–15 April 2015. [Google Scholar]
- Salmanpour, M.S.; Sharif, K.Z.; Aliabadi, M. Impact Damage Localisation with Piezoelectric Sensors under Operational and Environmental Conditions. Sensors 2017, 17, E1178. [Google Scholar] [CrossRef]
- Campos, R.; Gracias, N.; Ridao, P. Underwater Multi-vehicle Trajectory Alignment and Mapping Using Acoustic and Optical Constraints. Sensors 2016, 16, 387. [Google Scholar] [CrossRef]
- Mou, B.; He, B.J.; Zhao, D.X.; Chau, K.W. Numerical Simulation of the Effects of Building Dimensional Variation on Wind Pressure Distribution. Eng. Appl. Comput. Fluid 2019, 11, 293–309. [Google Scholar] [CrossRef]
- Ghalandari, M.; Koohshahi, E.M.; Mohamadian, F.; Shamshirband, S.; Chau, K.W. Numerical Simulation of Nanofluid Flow inside a Root Canal. Eng. Appl. Comput. Fluid 2019, 13, 254–264. [Google Scholar] [CrossRef]
- Jorge, P.; Beatriz, D.P.; Jesús, F.O.; Eduardo, B.M. A CFD Study on the Fluctuating Flow Field across a Parallel Triangular Array with One Tube Oscillating Transversely. J. Fluid Struct. 2018, 76, 411–430. [Google Scholar]
- Manoochehr, F.M.; Mohammad, T.S.; Mostafa, R. Numerical Simulation of the Hydraulic Performance of Triangular and Trapezoidal Gabion Weirs in Free Flow Condition. Flow Meas. Instrum. 2018, 62, 93–104. [Google Scholar]
- Hassan, E.S. Mathematical Description of the Stimuli to the Lateral Line System of Fish Derived from a Three-dimensional Flow Field Analysis. Biol. Cybern. 1992, 6, 443–452. [Google Scholar] [CrossRef]
- Humphrey, J.A. Drag Force Acting on a Neuromast in the Fish Lateral Line Trunk Canal II: Analytical Modelling of Parameter Dependencies. J. R. Soc. Interface 2009, 6, 641–653. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.S.; Vendhan, C.P.; Krishnankutty, P. Study of Water Wave Diffraction around Cylinders Using a Finite-element Model of Fully Nonlinear Potential Flow Theory. Ships Offsh. Struct. 2017, 12, 276–289. [Google Scholar] [CrossRef]
- Zhang, J.X.; Fan, X.; Liang, D.F.; Liu, H. Numerical Investigation of Nonlinear Wave Passing through Finite Circular Array of Slender Cylinders. Eng. Appl. Comput. Fluid 2019, 13, 102–116. [Google Scholar] [CrossRef]
- Song, X.W.; Qi, Y.C.; Zhang, M.X.; Zhang, G.G.; Zhan, W.C. Application and Optimization of Drag Reduction Characteristics on the Flow around a Partial Grooved Cylinder by Using the Response Surface Method. Eng. Appl. Comput. Fluid 2019, 13, 158–176. [Google Scholar] [CrossRef]
- Quezada, M.; Tamburrino, A.; Nino, Y. Numerical Simulation of Scour around Circular Piles Due to Unsteady Currents and Oscillatory Flows. Eng. Appl. Comput. Fluid 2018, 12, 354–374. [Google Scholar] [CrossRef]
- Barbier, C.; Humphrey, J.A.C. Drag Force Acting on a Neuromast in the Fish Lateral Line Trunk Canal. I. Numerical Modelling of External–Internal Flow Coupling. J. R. Soc. Interface 2009, 6, 627–640. [Google Scholar] [CrossRef]
- Zhou, H.; Hu, T.J.; Low, K.H.; Shen, L.C.; Ma, Z.W.; Wang, G.M.; Xu, H.J. Bio-inspired Flow Sensing and Prediction for Fish-like Undulating Locomotion: A CFD-aided Approach. J. Bionic Eng. 2015, 12, 406–417. [Google Scholar] [CrossRef]
- Singh, Y.; Bhattacharyya, S.K.; Idichandy, V.G. CFD Approach to Modelling, Hydrodynamic Analysis and Motion Characteristics of a Laboratory Underwater Glider with Experimental Results. J. Ocean Eng. Sci. 2017, 2, 90–119. [Google Scholar] [CrossRef]
- Tao, J.; Yu, X. Hair Flow Sensors: From Bio-inspiration to Bio-mimicking a Review. Smart Mater. Struct. 2012, 21, 113001. [Google Scholar] [CrossRef]
- Abdulsadda, A.T.; Tan, X. Nonlinear Estimation-based Dipole Source Localization for Artificial Lateral Line Systems. Bioinspir. Biomim. 2013, 8, 026005. [Google Scholar] [CrossRef] [PubMed]
- Abdulsadda, A.T.; Tan, X. An Artificial Lateral Line System Using IPMC Sensor Arrays. Int. J. Smart Nano Mater. 2012, 3, 226–242. [Google Scholar] [CrossRef]
- Dagamseh, A.M.K.; Lammerink, T.S.J.; Kolster, M.L.; Bruinink, C.M.; Wiegerink, R.J.; Krijnen, G.J.M. Dipole-source Localization Using Biomimetic Flow-sensor Arrays Positioned as Lateral-line System. Sens. Actuators A Phys. 2010, 162, 355–360. [Google Scholar] [CrossRef]
- Salumae, T.; Kruusmaa, M. Flow-relative Control of an Underwater Robot. Proc. R. Soc. A Math Phys. 2013, 469, 1–19. [Google Scholar] [CrossRef]
- Venturelli, R.; Akanyeti, O.; Visentin, F.; Jezov, J.; Chambers, L.; Toming, G.; Brown, J.; Kruusmaa, M.; Megill, W.M.; Fiorini, P. Hydrodynamic Pressure Sensing with an Artificial Lateral Line in Steady and Unsteady Flows. Bioinsper. Biomim. 2012, 7, 036004. [Google Scholar] [CrossRef]
- Fuentes-Perez, J.F.; Uhtan, J.A.; Baeza, R.C.; Musall, M.; Toming, G.; Muhammad, N. Current Velocity Estimation Using a Lateral Line Probe. Ecol. Eng. 2015, 85, 296–300. [Google Scholar] [CrossRef]
- Yang, Y.; Nguyen, N.; Chen, N.; Lockwood, M.; Tucker, C.; Hu, H.; Jones, D. Artificial Lateral Line with Biomimetic Neuromasts to Emulate Fish Sensing. Bioinspir. Biomim. 2010, 5, 16001. [Google Scholar] [CrossRef] [Green Version]
- Bao, Y.; Zhou, D.; Zhao, Y.J. A Two Step Taylor-characteristic-based Galerkin Method for Incompressible Flows and Its Application to Flow over Triangular Cylinder with Different Incidence Angles. Int. J. Numer. Methods Fluids 2010, 62, 1181–1208. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Zhao, X.Z.; Cheng, D.; Zhang, D.K.; Hu, Z.J. Numerical Study of Low-Reynolds-number Flow Past Two Tandem Square Cylinders with Varying Incident Angles of the Downstream One Using a CIP-based Model. Ocean Eng. 2016, 121, 414–421. [Google Scholar] [CrossRef]









| Case | Number of Elements | Percentage Changes/% | ||
|---|---|---|---|---|
| Grid-1 | 0.001H | 7.94 × 106 | 0.1418 | 0.77 |
| Grid-2 | 0.005H | 1.33 × 106 | 0.1429 | 3.99 |
| Grid-3 | 0.01H | 0.47 × 106 | 0.1486 | \ |
| 1.25 | 1.75 | 2.25 | 2.75 | 3.25 | |
|---|---|---|---|---|---|
| 1.26 | 1.74 | 2.23 | 2.73 | 3.28 | |
| 0.80 | 0.63 | 0.89 | 0.73 | 0.92 |
| (m/s) | 0.5 | 1.0 | 1.5 | 2.0 |
|---|---|---|---|---|
| 5.846 | 6.495 | 6.279 | 6.306 | |
| 0.573 | 0.746 | 0.685 | 0.652 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Wu, J.; Qin, Q. A Novel Obstacle Localization Method for an Underwater Robot Based on the Flow Field. J. Mar. Sci. Eng. 2019, 7, 437. https://doi.org/10.3390/jmse7120437
Lin X, Wu J, Qin Q. A Novel Obstacle Localization Method for an Underwater Robot Based on the Flow Field. Journal of Marine Science and Engineering. 2019; 7(12):437. https://doi.org/10.3390/jmse7120437
Chicago/Turabian StyleLin, Xinghua, Jianguo Wu, and Qing Qin. 2019. "A Novel Obstacle Localization Method for an Underwater Robot Based on the Flow Field" Journal of Marine Science and Engineering 7, no. 12: 437. https://doi.org/10.3390/jmse7120437
APA StyleLin, X., Wu, J., & Qin, Q. (2019). A Novel Obstacle Localization Method for an Underwater Robot Based on the Flow Field. Journal of Marine Science and Engineering, 7(12), 437. https://doi.org/10.3390/jmse7120437