T-Coin: Dynamic Traffic Congestion Pricing System for the Internet of Vehicles in Smart Cities

Abstract

Alleviating traffic congestion is one of the main challenges for the Internet of Vehicles (IoV) in smart cities. Many congestion pricing systems have been proposed recently. However, most of them focus on punishing the vehicles that use certain roads during peak hours, neglecting the proven fact that rewards can encourage drivers to follow the rules. Therefore, in this paper, we propose a new congestion pricing system based on reward and punishment policies for the IoV in a smart city environment, where the vehicles are rewarded for voluntarily choosing to take an alternative path to alleviate traffic congestion. The proposed system is implemented using vehicular ad hoc networks, which eliminate the need for installing a costly electronic toll collection system. We propose a new virtual currency called T-Coin (traffic coin), that is used to reward the vehicles for their positive attitude. T-Coin is also used in the tender between vehicles to manage the road reservation process. The proposed system uses dynamic pricing to adapt to peak-hour traffic congestion. Using simulated traffic on a real map of Beijing city, we prove the usefulness of T-Coin as a traffic congestion pricing system.

1. Introduction

According to a recent urban transportation report, in the USA, the economic loss caused by traffic congestion in terms of both fuel consumption and travel time delay was estimated at USD $121 billion in 2011 and is expected to reach USD $199 billion by 2020 [1]. In addition to its economic losses, traffic congestion is considered to be a significant contributor to CO2 emissions and global warming [2]. Traffic congestion is one of the most challenging problems that industrial and scientific communities are trying to solve nowadays.

There are two kinds of traffic congestion alleviation systems, physical-based systems and policy-based systems [3]. Physical-based systems involve changing the city road network structure to alleviate the congestion, such as creating new routes, adding more lanes, grade separation, and ramp signaling. Policy-based systems refer to the rules and regulations enacted by the authorities to reduce traffic congestion. There are many types of policies that can help to reduce traffic congestion which include the following: (1) Parking restrictions involve imposing more fees for parking in congested roads; (2) road space rationing involves preventing some types of vehicles from driving during a certain time or under certain circumstances or in certain areas, which can be based on plate number or other criteria such as passenger properties as workers, residents, disabled …etc.; (3) congestion pricing involves charging vehicles for using the roads. The congestion pricing system charges the vehicles for the use of certain roads (congested roads) during a certain time of the day such as peak hours. It is considered to be one of the most effective policy-based congestion alleviation techniques. There are two classes of congestion pricing, static pricing and dynamic pricing. Static pricing has no temporal dimension, thus, the pricing is fixed for using certain roads regardless of the time, which is not effective because it overcharges the vehicles for using an empty road in some cases, whereas dynamic pricing charges the vehicles for using certain roads only during certain times (usually congestion time). However, the main disadvantage of dynamic congestion pricing is that the system does not encourage the users to participate in the congestion alleviation process, because the road commuter is the main entity that is affected by the congestion and charging them for using the roads will make things worse.

Singapore was the first country that introduced the congestion pricing system in 1998 [4]. The system charges vehicles from 7:00 a.m. to 9:30 a.m. and from 5:30 p.m. to 10:30 p.m. during weekdays. Smart cards (CashCard) based on radio frequency identification (RFID) are used to detect and charge the vehicles. Similarly, the London congestion charging system was introduced in 2003 [5]. The system charges any private vehicle that drives into a congestion charge zone within weekdays from 7:00 a.m. to 6:00 p.m. on weekdays. These zones are made of a circle with a 2.7 km radius in the London central-city area. The city of Stockholm also implemented such a system in 2007 [6]. Many other cities wanted to introduce a congestion pricing system, but they failed to do so as a result of the lack of public support, and therefore political acceptability, that is, because they have focused on punishing vehicles that use certain roads during peak hours [7]. However, from a psychological perspective, it has been proven that rewards encourage drivers to willingly avoid congested roads [8].

Far from that, the emergence of vehicular ad hoc networks (VANETs) has provided a new class of congestion alleviation systems. VANETs can provide enhanced communication that supports both vehicle-to-vehicle (V2V) and vehicle-to-infrastructure (V2I) communications; VANETs can efficiently collect and report traffic updates from-and-to vehicles, as well as roadside units (RSUs). The collected real-time traffic information can be utilized for freeway traffic flow management, path planning, and vehicle localization. VANETs are applied in many traffic-related applications, such as collision avoidance [9], congestion alleviation [10], cyber-physical systems [11], Internet of Vehicles [12,13], and even mobile social media [14].

In this paper, we propose a new congestion pricing system based on reward and punishment policies, where the vehicles are rewarded for voluntarily choosing to take an alternative path to alleviate the traffic congestion. In addition, we propose a new virtual currency called T-Coin (traffic coin), that is used to reward the vehicles for their positive attitude. T-Coin is also used in the tender between vehicles to manage the road reservation process. The proposed system uses dynamic pricing to adapt to peak-hour traffic congestion. Using simulated traffic on a real map of Beijing city, we have proven the usefulness of T-Coin as a traffic congestion pricing system.

Our main contributions can be summarized as follows:

• We propose a traffic control system that is based on road reservations, and therefore the proposed system ensures that the congestion never takes place;
• T-Coin is based on reward and punishment to encourage the drivers to take alternative paths that could alleviate traffic congestion;
• The path reservation can be traded among vehicles through a tender process, which prioritizes urgent path requests;
• A dynamic pricing model based on road length, road importance, and current traffic congestion is proposed.

The remainder of the paper is organized as follows: In Section 2, we present previous related works on congestion pricing and traffic optimization; in Section 3, we explain the main rules of the proposed system; in Section 4, the modeling details of the proposed system are presented; Section 5 presents the performance evaluation and simulation details; whereas in Section 6, the result of the simulation is analyzed; and finally, in Section 7, we conclude the paper and give some future directions.

2. Related Works

Many works have discussed congestion pricing systems. In this section, we review the most relevant works that have investigated the topic.

De Palma et al. [3] surveyed the methods and technologies for congestion pricing of roads. Congestion pricing using optimal control theory was discussed in [15], where the authors presented a mathematical model for dynamic congestion pricing. The proposed model was realized using queuing theory, traffic conservation law, and fundamental macroscopic relationships. They proposed a cost function and used the Hamilton–Jacobi–Bellman equation to derive an optimal control law that used real-time information to determine an optimal tolling price. Marefat et al. [16] discussed the feasibility of using VANET instead of the traditional radio frequency identification (RFID) to implement congestion pricing and proved the superiority of the VANET-based pricing system, as the RFID-based systems suffer from several limitations such as low data rate, low transmission range, as well as other communication drawbacks such as delay, tag and reader collisions, signal fading, and interception. The proposed system is evaluated using simulation tools, specifically NS-2, SUMO, and TraNS. Kachroo et al. [17] studied the control design of dynamic congestion pricing as a way to implement traffic assignments to satisfy a given objective. The proposed design made use of the optimal control theory and permitted the modeling of tolled and non-tolled routes or lanes. A logit-based model links the toll cost and driver choices. An optimal tolling control law was realized based on the Hamilton–Jacobi–Bellman equation. Zhou et al. [18] proposed a framework to model the lane and path choices and dynamically estimated the toll cost according to the current traffic conditions. In the proposed method, the high-occupancy toll lanes can better use the road resources by letting low-occupancy vehicles pay a toll and drive in the high-occupancy vehicle lanes. Whereas Tscharaktschiew et al. [19] investigated the effects of the switch in automated driving mode on the road congestion pricing and vice versa. They discussed the relationship between the autonomous driving level, marginal travel price, and road capacity, while other works have discussed the drivers’ privacy and malicious vehicle detection in congestion pricing systems. Bouchelaghem et al. [20] proposed a reliable and secure road pricing system, which detects evasive drivers that avoid paying the toll. The proposed method works under a complete distributed threshold-based control system to reveal dishonest drivers that are trying to avoid paying their tolls. Following the detection phase, the malicious drivers are reported to the traffic control server to apply the relevant punishment. The proposed system is evaluated by means of simulation based on two main metrics, storage and communication overheads. Jardí-Cedó et al. [21] proposed an electronic road pricing (ERP) system, made especially for cities with multifare low-emission zones. The purpose of the proposed system is to reveal fraudulent vehicles and preserve the drivers’ privacy.

Zhang et al. introduced DIFTOS [22], a complete distributed and infrastructure-free congestion alleviation system for VANET, in which the city map is represented as a hierarchy of distributed vehicular servers. The clusters of cars that are satiated in the congested road intersections act as virtual servers, in this way, DIFTOS does not depend on any centralized traffic control server and does not rely on internet connectivity or roadside units. Jeong et al. [23] presented a traffic optimization system named SAINT (self-adaptive interactive navigation tool). SAINT is customized for traffic optimization using cloud-based vehicular networks, in which individual network nodes submit the congestion status within their travel paths to the centralized vehicular cloud. On the basis of the submitted reports by the network nodes, the traffic control center uses a mathematical model to compute the global optimized path for each vehicle with respect to other network nodes. SAINT was applied by Shen et al. [24] for an emergency management framework called SAINT+, which used vehicular-to-vehicular communication to decrease the response time of emergency services in case of traffic accidents. Pan et al. [25] introduced DIVERT for vehicular networks which is a distributed rerouting and congestion avoidance system. DIVERT uses the vehicles to help the server compute the optimal paths, and therefore the rerouting decisions are possible to perform in real time. However, DIVERT is not a completely infrastructure-free system because it still depends on a centralized server through 4G internet connectivity to coordinate the computing between vehicles.

However, the proposed system significantly differs from the abovementioned congestion alleviation systems in many aspects.

Table 1. Features comparison between T-Coin and state-of-the-art systems.

	System	T-Coin	DIFTOS	SAINT	DIVERT
Feature
Traffic Control Center		Centralized server	Hierarchal distributed vehicular servers	Centralized server	Distributed servers
Road reservation strategy		First come first served + Tender process	First come first served	First come first served	First come first served
Communication infrastructure dependency (V2I+4G)		Infrastructure required	Infrastructure not required	Infrastructure required	Infrastructure partially required
Rerouting strategy		Yes	Yes	Yes	Yes
Quota allocation		Yes	Yes	No	No
Driver decides rerouting path		Yes	No	No	No
Virtual currency		Yes	No	No	No
Destination-aware rerouting prioritization		Yes	No	No	No

shows a comparison in terms of the offered features and architectural design of each system.

3. System Policies

In this section, we explain the rules and policies of the proposed system.

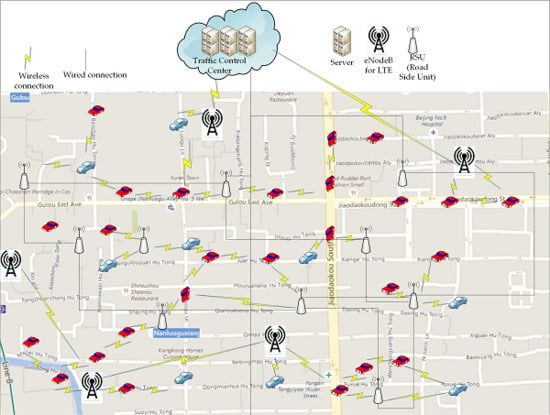
3.1. Vehicular Navigation Architecture

The required infrastructure and vehicular communication equipment of the proposed system, as shown in Figure 1, are presented as follows:

• Traffic Control Center (TCC) TCC is a server that manages the path reservation process. It maintains the road reservation matrix (RRM) that contains the information about the number of reserved, as well as free, positions in each road segment during different time slots. The TCC updates traffic statistics such as average speed per road segment and vehicle arrival rate and is also responsible for computing road pricing and managing T-Coin transactions between vehicles in the case of the tender process. For a large-scale road network, a single TCC is not able to maintain the traffic updates for such a huge number of vehicles. To solve this scalability problem, the road network could be segmented into multiple regions, where each region is managed by its own TCC, and the TCCs communicate with each other to resolve cross regional paths. The design of the TCC server is left as future work.
• Roadside Unit (RSU) An RSU is a wireless gateway that connects the vehicles to the wired network (i.e., the Internet). The RSU and the vehicles communicate through dedicated short-range communication (DSRC). Generally, RSUs are deployed near the intersection and they are connected to each other using a wired network. RSUs are considered to be the backbone of the communication network that connects the wirelessly connected vehicles to the TCC.
• eNodeB In the case of RSU failure or disconnectivity between the RSU and the vehicle due to the DSRC range limit, the vehicles could also connect to the TCC through eNodeB which is a base station that connects the vehicle to the 4 G-LTE cellular network. It enables the vehicles to access the TCC in a ubiquitous way.
• Vehicles To communicate with RSUs and eNodeBs, all the vehicles are equipped with a DSRC communication device embedded in their on-board unit (OBU). They are also equipped with a GPS-based navigation system that has a digital roadmap. The Vehicles report the updates about their travel experience in road segments and at intersections along their travel path to the traffic control center. Since the travel paths are very sensitive information, all the communications between vehicles and the server are encrypted.

3.2. T-Coin Balance

To implement the congestion pricing system, we have proposed a new virtual currency called T-Coin (traffic coin) that is used to reward and punish the vehicles for their behaviors; in addition, T-Coin is used as a currency in the tender between vehicles to manage the road reservation process. Vehicles can acquire T-Coin using one of the following ways: (1) By directly buying it in exchange with real currencies such as USD, EUR, RMB, …, etc.; or (2) by earning it as a reward for their good behaviors, such as their desire to take an alternative path, other than their shortest path, to alleviate the traffic congestion; or (3) by selling their road reservations to other vehicles that have urgent situations using a tender process.

3.3. Road Reservation Policy

To avoid traffic congestion on city roads, the roads’ capacity is divided into two parts (traffic quotas). The first quota can be reserved free of charge. When the free traffic quota is fully reserved, vehicles who choose to use the road need to pay a specific amount of T-Coin to reserve the road. The roads are reserved using a first-come first-served policy. In other words, roads are reserved for the first vehicles that express their desire to use them. When a new vehicle joins the network, it sends a path request that contains its source and destination’s GPS coordinates to the server. The latter computes the shortest path, as well as the free path (the shortest path that uses only free of charge traffic quota) from the source to the destination. The server does this by estimating the arrival time to each road segment in both paths, thus the server can estimate the expected traffic flow in each road segment during different time periods.

3.4. Reward and Punishment Policy

After computing the shortest path ((2) in Figure 2) and the free path ((1) in Figure 2), the driver decides which path the vehicle takes. If the vehicle chooses to take the shortest path, it is punished for using a congested road during rush hour and has to pay, in T-Coin, the sum of all the paid traffic quota in each road segment in its shortest path, whereas if the vehicle chooses to take the free path, it is rewarded in T-Coin, estimated by the difference of travel delays between the shortest path and the free path.

3.5. Traffic Tender

In addition to the shortest path and the free path, the server also recommends a set of roads, named critical roads, that are fully reserved, but in the case that they were free, they would greatly decrease the travel delay from source to destination. In this case, the driver is willing to pay to use these roads. It calls for a traffic tender on these road segments. The tender follows the hidden envelope best price model, in which the vehicle broadcasts a message with the critical road segments’ IDs to express its willingness to pay T-Coins to use these roads. The tender request message also includes the deadline of the tender. After receiving the tender offers, if the vehicle (driver) confirms the offered price, it sends a path update to the server, and the confirmed bidders receive the specified T-Coin amounts. The detailed steps of road reservation and traffic tender process is descripted in Figure 3.

3.6. Misbehaviors Punishment

The proposed system is based on the road reservation process, which ensures that road segments are used within their capacity. In order to use a road segment, the road segment must be within the pre-reserved path that was assigned to the vehicle by the TCC. Any violation of the road reservation process leads to road congestion. Therefore, vehicles that violate the reservation policy and use the roads without prior reservations are punished by reducing their T-Coin balance, or other legal punishment by the authorities.

4. System Model

In this section, we explain the modeling details of the proposed system. It is worth mentioning that the modeling of city map graph network, traffic flow, and travel delay modeling have been adapted from our previous work, i.e., DIFTOS [22].

4.1. Map Modeling

To facilitate the computation of the shortest path, the map of the studied city is represented as a directed weighted graph. Let $\mathit{G}=\left(\mathit{I},\mathsf{\Omega },\mathbf{V}\right)$ be a directed weighted graph that represents the road network of the studied city. Let $\mathsf{\Omega }$ be the set of directed road segments, and I be the set of road segment intersections. While $\mathit{V}$ denote the set of vehicles in the city map. The road segments are bidirectional with one lane or more in each direction.

4.2. Traffic Flow and Travel Delay

To model the traffic flow and travel delay, the temporal representation is modeled as a set of consecutive time intervals $\mathit{T}=\left\{{\mathit{t}}_{\mathbf{1}},{\mathit{t}}_{\mathbf{2}},\dots ,{\mathit{t}}_{\mathit{n}}\right\}$. The traffic condition on a given road is determined by measuring the traffic flow in that road during the corresponding time slot. The traffic flow in the road section ${\mathit{r}}_{\mathit{i},\mathit{j}}$ in the time interval $\mathit{t}$ is represented as ${\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{t}}$ and is computed by calculating the mean of the speed ${\mathsf{\vartheta }}_{\mathit{i},\mathit{j}}^{\mathit{t}}$ of all the vehicles running in the traffic flow on this road section within the time interval $\mathit{t}$ [26], see Equation (1):

$$x_{i,j}^t= E\left({\vartheta }_{i,j}^t\left(v_k\right) \right).$$

(1)

${\mathsf{\vartheta }}_{\mathit{i},\mathit{j}}^{\mathit{t}}\left({\mathit{v}}_{\mathit{k}}\right)$ denotes the velocity of the vehicle ${\mathit{v}}_{\mathit{k}}$ in the road section ${\mathit{r}}_{\mathit{i},\mathit{j}}$ within the time interval $\mathit{t}$. To determine the mean velocity of traffic flow, the average velocity of all vehicles on the road section during the time interval is computed. In this regard, we assume that during each time interval, the traffic situation on a given road section is uniform. The data of the average speed for every road section is determined based on the vehicles’ travel experience reports, as well as the vehicular traffic calculation using the roads’ loop detectors [27].

Let ${\mathit{d}}_{\mathit{i},\mathit{j}}$ be the delay period required to cross ${\mathit{r}}_{\mathit{i},\mathit{j}}$, ${\mathit{d}}_{\mathit{i},\mathit{j}}$ is the ceiled number of time intervals necessary for a vehicle to pass the road section ${\mathit{r}}_{\mathit{i},\mathit{j}}$ that its length is ${\mathit{l}}_{\mathit{i},\mathit{j}}$ and the traffic situation ${\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{t}}$, noting that ${\mathit{d}}_{\mathit{i},\mathit{j}}$ also encompass the waiting time at the intersection ${\mathit{\omega }}_{\mathit{j}}$ that the vehicle wait to get out of intersection $\mathit{j}$ before passing to the following road segment ${\mathit{r}}_{\mathit{j},\mathit{k}}$. Thus, the crossing travel delay for the road section ${\mathit{r}}_{\mathit{i},\mathit{j}}$ is calculated as in Equation (2):

$${\mathrm{d}}_{\mathrm{i},\mathrm{j}}=\raisebox{1ex}{${\mathrm{l}}_{\mathrm{i},\mathrm{j}}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{x}}_{\mathrm{i},\mathrm{j}}^{\mathrm{t}}$}\right.+{\mathsf{\omega }}_{\mathrm{j}}.$$

(2)

Within a given time interval ${\mathit{t}}_{\mathit{x}}$, any road segment ${\mathit{r}}_{\mathit{i},\mathit{j}}$ is affiliated with a weight, represented as ${\mathit{w}}_{\mathit{i},\mathit{j}}\left(\mathit{x}\right)$, that is updated dynamically in each time interval based on the road reservation process, and it can be calculated as shown in Equation (3):

$${\mathrm{w}}_{\mathrm{i},\mathrm{j}}\left(\mathrm{x}\right)={\mathrm{C}}_{\mathrm{i},\mathrm{j}}-{\mathrm{Ř}}_{\mathrm{i},\mathrm{j}}\left(\mathrm{x}\right).$$

(3)

${\mathrm{Ř}}_{\mathit{i},\mathit{j}}\left(\mathit{x}\right)$ is the count of occupied positions in the road section ${\mathit{r}}_{\mathit{i},\mathit{j}}$ during time interval ${\mathit{t}}_{\mathit{x}}$.

${\mathit{C}}_{\mathit{i},\mathit{j}}$ denotes the capacity of the road section, ${\mathit{r}}_{\mathit{i},\mathit{j}}$, that is the maximum count of vehicles that can simultaneously pass the road section ${\mathit{r}}_{\mathit{i},\mathit{j}}$ so that the road is still not congested. Let ${\mathit{V}}_{\mathit{i},\mathit{j}}=\left({\mathit{v}}_{\mathit{i},\mathit{j}}^{\mathit{1}},{\mathit{v}}_{\mathit{i},\mathit{j}}^{\mathbf{2}},\dots ,{\mathit{v}}_{\mathit{i},\mathit{j}}^{\mathit{n}}\right)$ be a group of vehicles that are passing through the road section ${\mathit{r}}_{\mathit{i},\mathit{j}}$ at the same time, we consider ${\mathit{r}}_{\mathit{i},\mathit{j}}$ as a congested road section if Equation (4) is satisfied, that is to say, if the difference of the accumulated link delay time of all vehicles in ${\mathit{V}}_{\mathit{i},\mathit{j}}$ and the delay time of ${\mathit{r}}_{\mathit{i},\mathit{j}}$ multiplied by the number of vehicles in the group $\mathit{n}$ is more than or equal to the road congestion threshold $\mathsf{\epsilon }$,

$${\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{n}}{\mathrm{d}}_{\mathrm{i},\mathrm{j}}^{\mathrm{k}}-\left(\mathrm{n}\times {\mathrm{d}}_{\mathrm{i},\mathrm{j}}\right) \ge \mathsf{\epsilon }$$

(4)

where ${\mathit{d}}_{\mathit{i},\mathit{j}}^{\mathit{i}}$ is the link delay time of vehicle ${\mathit{v}}_{\mathit{i}}$ when passing through ${\mathit{r}}_{\mathit{i},\mathit{j}}$.

4.3. Path Reservation Process

4.3.1. Road Reservation Matrix

Let $\mathsf{\Omega }$ be the set of all road segments within the city map $\mathsf{\Omega }=\left\{{\mathit{r}}_{\mathbf{0}},{\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}},\dots ,{\mathit{r}}_{\mathit{N}-\mathbf{1}}\right\}$, and $\mathit{T}$ is a series of successive time intervals $\mathit{T}=\left\{{\mathit{t}}_{\mathbf{0}},{\mathit{t}}_{\mathbf{1}},{\mathit{t}}_{\mathbf{2}},\dots ,{\mathit{t}}_{\mathit{M}-\mathbf{1}}\right\}$, the procedure of reservation of $\mathsf{\Omega }$ during $\mathit{T}$ is maintained by keeping track of the road reservation matrix, denoted as ${\mathit{M}}_{\mathsf{\Omega },\mathit{T}}={\left({\mathit{w}}_{\mathit{r},\mathit{t}}\right)}_{\mathit{m}\times \mathit{n}}$, where ${\mathit{w}}_{\mathit{r},\mathit{t}}$ is the weight of the road section ${\mathit{r}}_{\mathit{i},\mathit{j}}$ during time interval $\mathit{t}$. The road reservation matrix includes the weights of every road section of $\mathsf{\Omega }$, within every time intervals in $\mathit{T}$, as the weights are updated dynamically with regard to the road demands and reservation process, ${\mathit{M}}_{\mathsf{\Omega },\mathit{T}}$ is maintained and updated by the TCC.

4.3.2. Traffic Quota Management

As mentioned earlier, the roads’ capacity is divided into two quotas (free quota and paid quota). The free quota can be reserved free of charges. When the free traffic quota is fully reserved, vehicles who choose to use the road need to pay a specific amount of T-Coin to reserve the road. The capacity of the paid traffic quota changes dynamically according to the road demand in the near past (the previous time slots), the more the road demand increases, the more its paid traffic quota increases. To model the traffic quotas dynamic segmentation, we proposed a traffic quota allocation algorithm. The proposed algorithm is inspired by TCP’s congestion control algorithm AIMD (additive increase multiplicative decrease) and is presented in Algorithm 1.

Algorithm 1. Congestion aware traffic quota allocation.

1: $\sigma =\lceil C_{i,j}/100\rceil$

2:      if $(M_{r_{i,j},t}< Q_{i,j}^T)$ then

3:         $\delta \leftarrow (M_{r_{i,j},t}-Q_{i,j}^T)$

4:         $Q_{i,j}^c\left(t+1\right)\leftarrow Q_{i,j}^c\left(t\right)+\delta$

5:      else

6:         if ($Q_{i,j}^c\left(t\right)< Q_{i,j}^T$) then

7:           $Q_{i,j}^c\left(t+1\right)\leftarrow Q_{i,j}^c\left(t\right)-\sigma$

8:         end if

9:      end if

Where $Q_{i,j}^T$ is the paid quota threshold. It is a fixed constant that is to mark the limit of the paid traffic quota, when the road demand surpasses this threshold, the paid quota for this road segment will increase dynamically based on the future road demand. $Q_{i,j}^c$ is the currently paid traffic quota, $\sigma$ is the additive increase parameter and we have set it as 1% of the total capacity of the road segment, and $\delta$ is the multiplicative decrease factor which we have set as the number of vehicles that are using the paid traffic quota.

4.4. Dynamic Congestion Pricing

4.4.1. Punishment Pricing

One of the first questions that is raised by the system users is “what is the price of using a given road?” This question cannot be answered directly because we have used multifactor dynamic pricing for the paid road reservation. Our proposed pricing strategy basically depends on the following three factors: (1) the length of the road segment, (2) the road demand during the reservation request time slot, and (3) the importance of the road in the vehicle’s path. The dynamic pricing function is defined in Equation (5):

$$\begin{gathered} {\mathsf{\phi }}_{\mathrm{i},\mathrm{j}}^{\mathrm{v}}\left(\mathrm{t}\right)=\mathrm{f}\left({\mathrm{l}}_{\mathrm{i},\mathrm{j}}\right)\times \mathrm{g}\left({\mathrm{Q}}_{\mathrm{i},\mathrm{j}}^{\mathrm{p}}\left(\mathrm{t}\right)\right)\times \mathrm{h}\left({\mathrm{r}}_{\mathrm{i},\mathrm{j}}^{\mathrm{v}}\left(\mathrm{t}\right)\right) \\ ={\tilde{l}}_{i,j}\times {\tilde{d}}_{i,j}\left(t\right)\times {\tilde{r}}_{i,j}^v\left(t\right) \end{gathered}$$

(5)

where $\mathrm{f}\left({\mathrm{l}}_{\mathrm{i},\mathrm{j}}\right)$ are the pricing functions that map the road length to the equivalent amount in T-Coin,

$$\begin{gathered} \mathrm{f}\left({\mathrm{l}}_{\mathrm{i},\mathrm{j}}\right)\to { \tilde{\mathrm{l}}}_{\mathrm{i},\mathrm{j}} \\ {\tilde{\mathrm{l}}}_{\mathrm{i},\mathrm{j}}={\mathrm{l}}_{\mathrm{i},\mathrm{j}}\times \mathsf{\tau } \end{gathered}$$

(6)

where $\tau$ is the road toll rate and is determined by the local authorities. In our simulation, we assumed that $\tau =1\raisebox{1ex}{$\mathrm{TCoin}$}\!\left/ \!\raisebox{-1ex}{$km$}\right.$.

$\mathrm{g}\left({\mathrm{Q}}_{\mathrm{i},\mathrm{j}}^{\mathrm{p}}\left(\mathrm{t}\right)\right)$ is the road demand function, which is the linear transformation of the traffic demand on the road $r_{i,j}$ during time slot $t$ (the value of ${\mathrm{Q}}_{\mathrm{i},\mathrm{j}}^{\mathrm{p}}\left(\mathrm{t}\right)$ presented in Algorithm 1), to the road demand factor, denoted as ${\tilde{d}}_{i,j}\left(t\right)$.

$$\begin{gathered} \mathrm{g}\left({\mathrm{Q}}_{\mathrm{i},\mathrm{j}}^{\mathrm{p}}\left(\mathrm{t}\right)\right)\to {\tilde{\mathrm{d}}}_{\mathrm{i},\mathrm{j}}\left(\mathrm{t}\right) \\ 1<{\tilde{d}}_{i,j}\left(t\right)<2 \\ {\tilde{\mathrm{d}}}_{\mathrm{i},\mathrm{j}}\left(\mathrm{t}\right)=\frac{({\mathrm{c}}_{\mathrm{i},\mathrm{j}}-{\mathrm{Q}}_{\mathrm{i},\mathrm{j}}^{\mathrm{p}}\left(\mathrm{t}\right))}{{\mathrm{c}}_{\mathrm{i},\mathrm{j}}}+1 \end{gathered}$$

(7)

$\mathrm{h}\left({\mathrm{r}}_{\mathrm{i},\mathrm{j}}^{\mathrm{v}}\left(\mathrm{t}\right)\right)$ is the road importance function, it represents the importance of the road, $r_{i,j}$, in the vehicle’s, $v$’s, path toward its destination; $h$ computes the best alternative path from intersection $i$ to $v$’s destination point, denoted as ${\ddot{p}}_{i,s}^r\left(t\right)$; the output of $h$ is the importance factor, denoted as ${\tilde{r}}_{i,j}^v\left(t\right)$, and is computed based on the delay ratio of ${\ddot{p}}_{i,s}^r\left(t\right)$ and $p_{i,s}\left(t\right)$, as shown in Equation (8). In other words, if the delay of the alternative path is double the delay if vehicle $v$ takes the road $r_{i,j}$, then this road is considered as a critical road for vehicle $v$, and the importance factor will be 1, thus it does not increase the total cost ${\phi }_{i,j}^v\left(t\right)$.

$$\begin{gathered} \mathrm{h}\left({\mathrm{r}}_{\mathrm{i},\mathrm{j}}^{\mathrm{v}}\left(\mathrm{t}\right)\right)\to {\tilde{\mathrm{r}}}_{\mathrm{i},\mathrm{j}}^{\mathrm{v}}\left(\mathrm{t}\right) \\ 1<{\tilde{r}}_{i,j}^v\left(t\right)<2 \\ {\tilde{\mathrm{r}}}_{\mathrm{i},\mathrm{j}}^{\mathrm{v}}\left(\mathrm{t}\right)=\left\{\begin{array}{cc}\hspace{1em}\hspace{1em}1,& \frac{\mathrm{d}\left({\ddot{\mathrm{p}}}_{\mathrm{i},\mathrm{s}}^{\mathrm{r}}\left(\mathrm{t}\right)\right)}{\mathrm{d}\left({\mathrm{p}}_{\mathrm{i},\mathrm{s}}\left(\mathrm{t}\right)\right)}>2\\ \frac{\mathrm{d}\left({\ddot{\mathrm{p}}}_{\mathrm{i},\mathrm{s}}^{\mathrm{r}}\left(\mathrm{t}\right)\right)}{\mathrm{d}\left({\mathrm{p}}_{\mathrm{i},\mathrm{s}}\left(\mathrm{t}\right)\right)},& \mathrm{else}\end{array}\right. \end{gathered}$$

(8)

4.4.2. Reward Pricing

The reward for choosing to avoid the congested path is denoted as ${\mathsf{\delta }}_{i,j}^v\left(t\right)$ and is computing as shown in Equation (9):

$${\mathsf{\delta }}_{\mathrm{i},\mathrm{j}}^{\mathrm{v}}\left(\mathrm{t}\right)=\left\{\begin{array}{c}{\mathrm{w}}_{\mathrm{i},\mathrm{j}}\left(\mathrm{t}\right)> {\mathrm{Q}}_{\mathrm{i},\mathrm{j}}^{\mathrm{p}}\left(t\right),{\mathsf{\delta }}_{\mathrm{i},\mathrm{j}}^{\mathrm{v}}\left(\mathrm{t}\right)=\frac{\mathrm{f}\left({\mathrm{l}}_{\mathrm{i},\mathrm{j}}\right)\times \mathrm{g}\left({\mathrm{Q}}_{\mathrm{i},\mathrm{j}}^{\mathrm{p}}\left(\mathrm{t}\right)\right)}{\mathrm{h}\left({\mathrm{r}}_{\mathrm{i},\mathrm{j}}^{\mathrm{v}}\left(\mathrm{t}\right)\right)}\\ \mathrm{else},{\mathsf{\delta }}_{\mathrm{i},\mathrm{j}}^{\mathrm{v}}\left(\mathrm{t}\right)=0\end{array}\right.$$

(9)

5. Performance Evaluation

In this section, we present the evaluation baselines, metrics, and the simulation parameters.

5.1. Baselines

To test the performance of the proposed system we have compared the performance of the following baselines:

Dijkstra Fixed T-Coin (DFT) Since Dijkstra shortest path algorithm as a most intuitive path assignment method, we implement a system (hereafter referred to as DFT) that uses the Dijkstra algorithm to determine the shortest path from the starting point to the destination point. The vehicle will go through that path regardless of the traffic conditions within the roads of the path, where each road segment has a fixed traffic quota.

Fixed Pricing T-Coin (FP T-Coin) To test the usefulness of adaptive pricing and quota allotment functions of the proposed system, we have implemented a static version of the proposed system (hereafter abbreviated as FP T-Coin) and make it as a baseline, in which we make the paid traffic quota as a fixed amount, thus, the paid quota will remain the same regardless of the traffic congestion.

Adaptive Pricing T-Coin (AP T-Coin) This is the proposed system (hereafter abbreviated as AP T-Coin).

5.2. Performance Metrics

We have considered the following metrics to be evaluated and compared with the performance of the abovementioned baselines:

Additional Distance (traveled distance/shortest distance) This metric is used to measure the additional distance that the vehicle has traveled as compared with the distance of its shortest path from the starting point to the destination point. In other words, we compute the ratio of the actual traveled distance from the starting point to the destination point as compared with the distance from the starting point to the destination point using the shortest path. We denote the additional distance of the vehicle $v_i$ as $AD\left(v_i\right)$, see Equation (10), and the total additional distance of all vehicles is computed in Equation (11).

$$\mathrm{AD}\left(\mathrm{v}\right)= \frac{{{\displaystyle \sum }}_{\mathrm{i}=0}^{\mathrm{m}-1}{\mathrm{l}}_{\mathrm{i}}^{\mathrm{f}}}{{{\displaystyle \sum }}_{\mathrm{i}=0}^{\mathrm{n}-1}{\mathrm{l}}_{\mathrm{i}}^{\mathrm{s}}},$$

(10)

where ${\mathrm{p}}_{\mathrm{i}}^{\mathrm{s}}=\left\{{\mathrm{r}}_1^{\mathrm{s}},{\mathrm{r}}_2^{\mathrm{s}},\dots ,{\mathrm{r}}_{\mathrm{n}}^{\mathrm{s}}\right\}$ and ${\mathrm{p}}_{\mathrm{i}}^{\mathrm{f}}=\left\{{\mathrm{r}}_1^{\mathrm{f}},{\mathrm{r}}_2^{\mathrm{f}},\dots ,{\mathrm{r}}_{\mathrm{m}}^{\mathrm{f}}\right\}$ are the shortest path and the shortest free path of the vehicle $v_i$, respectively, $l_i^f$ and $l_i^s$ are the lengths of road $r_i^f$ and road $r_i^s$, respectively.

$$\mathrm{AD}\left(\mathrm{V}\right)=\frac{{{\displaystyle \sum }}_{\mathrm{i}=0}^{\mathrm{p}-1}\mathrm{AD}\left({\mathrm{v}}_{\mathrm{i}}\right)}{\mathrm{p}},$$

(11)

where $V=\left\{v_0,v_1,\dots ,v_{p-1}\right\}$ is the set of the simulated vehicles.

Additional Time (traveling time/estimated traveling time) This metric is used to measure the additional time that the vehicles have consumed in order to reach their final destination as compared with the initial estimated time of the shortest path. In other words, we compute the ratio of the actual traveling time from the starting point to the destination point, and the traveling time starting point to the destination point using the shortest path. We denote the additional time of vehicle $v_i$ as $AT\left(v_i\right)$, and it can be computed as in Equation (12), and the total additional time of all vehicles is computed as in Equation (13).

$$\mathrm{AT}\left(\mathrm{v}\right)= \frac{{{\displaystyle \sum }}_{\mathrm{i}=0}^{\mathrm{m}-1}{\mathrm{d}}_{\mathrm{i}}^{\mathrm{f}}}{{{\displaystyle \sum }}_{\mathrm{i}=0}^{\mathrm{n}-1}{\mathrm{d}}_{\mathrm{i}}^{\mathrm{s}}},$$

(12)

where $p_i^s=\left\{r_1^s,r_2^s,\dots ,r_n^s\right\}$ and $p_i^f=\left\{r_1^f,r_2^f,\dots ,r_m^f\right\}$ are the shortest path and the shortest free path of the vehicle $v_i$, respectively, and $d_i^f$ is the travel delay of road $r_i^f$, and $d_i^s$ is the travel delay of road $r_i^s$.

$$\mathrm{AT}\left(\mathrm{V}\right)=\frac{{{\displaystyle \sum }}_{\mathrm{i}=0}^{\mathrm{p}-1}\mathrm{AT}\left({\mathrm{v}}_{\mathrm{i}}\right)}{\mathrm{p}},$$

(13)

where $V=\left\{v_0,v_1,\dots ,v_{p-1}\right\}$ is the set of vehicles in the city.

T-Coin Gain This metric is used to measure the total gained T-Coin, in which we compute the total gained T-Coin from paid traffic punishments and the total lost T-Coin that was given as a reward for alleviating congestion, see Equation (14):

$$\mathrm{G}={{\displaystyle \sum }}_{\mathrm{r}=0}^{\mathrm{n}-1}{\mathrm{P}}_{\mathrm{r}}-{{\displaystyle \sum }}_{\mathrm{r}=0}^{\mathrm{n}-1}{\mathrm{R}}_{\mathrm{r}}.$$

(14)

5.3. Evolution Parameters

In the performance evaluation, we investigated the impact of vehicle density on system performance. The vehicle density is the number of vehicles involved in the simulation, and it is the most important parameter because it is the direct cause of road congestion. Each time we tested the system under different vehicle density values and observed the effect on the system’s performance, by increasing this parameter to high values we could evaluate the robustness and scalability of the system under heavy traffic conditions.

5.4. Simulation Environment

The simulation was performed on a real map of a part of Beijing city. The simulated map was extracted from OpenStreetMap [28]. The area of 4.5 km² was extracted by specifying the GPS coordinates of the desired area. The road network was extracted from the raw map using the simulation of urban mobility platform SUMO [29], see Figure 4. The proposed system was simulated using Omnet++ network simulator by implementing vehicular behaviors with the vehicular framework Veins [30]. The simulation parameters are depicted in

Table 2. Simulation parameters.

Parameters	Description
Network Simulator	Omnet++5
Traffic Simulator	Sumo 0.27.1
Map Information	OpenStreetMap
Simulated Location	Beijing
Simulated area	$4.5 \mathrm{k}{\mathrm{m}}^2$

. During the simulation, three modules ran simultaneously. Veins was responsible for the network simulation, while SUMO ran the road traffic simulation and sumo-launched acted as a broker between the two modules. SUMO dynamically updates the traffic-related values through the Traci interface, as shown in Figure 5.

The details of the simulation tools and the city map are presented in Table 1 and Table 2. While a detailed description of the wireless communication model used in the simulation is described in

Table 3. Wireless communication parameters.

Parameter	Value
PHY model	802.11 p
Channel frequency	5.890e9 Hz
Propagation model	Two ray
MAC model	EDCA
Propagation distance	450 m
Maximum hop	15
Fading model	Jakes model rayleigh fading
Shadowing model	LogNormal
Antenna model	Omnidirectional
Transmission power	20 mW

.

The vehicles joined the network and were randomly placed at one intersection as a starting position and moved toward another randomly selected intersection as the ending position, however, we adjusted the fringe factor to 10, which means edges that were at the fringe of the network were 10 times more likely to be chosen as the start or endpoint of a trip, which helped us to model a long trip. Moreover, the minimum trip distance was set to double of the average road length, because a meaningful route should have at least two consecutive roads, and the traffic lights were also set as static, which means every traffic light had a fixed duration regardless of the traffic conditions. That allowed us to estimate the expected arrival time in the road reservation process. Vehicles traveled toward their destinations with a velocity of 30 to 60 km/h. The presented results are the average of 100 simulation runs.

6. Results Discussion

First, we evaluated the three systems (DFT, FPT, and APT), in terms of AD, AT, and TG, under different density scenarios, the results of density test are presented in Figure 6, Figure 7 and Figure 8. As shown in Figure 6, in low-density scenarios (under 500 vehicles), the AT of the three systems is almost negligible. However, starting from medium-density (500 to 3000) and high-density (3000 to 9000) scenarios, all of the three schemes’ AT increase relative to the density increase, but at different rates. The DFT’s AT increases dramatically with the increase of vehicle density, to reach an AT of 2.2 at the highest density scenario (9000), that is to say, at 9000 vehicles density, on average the vehicle’s traveling time to its destination is as high as 220% as compared with the initial estimated time of the shortest path, that is because vehicles under DFT scheme always choose the shortest path even if it’s congested. Unlike DFT, FTP’s and APT’s AT moderately increase to reach 1.5 at the highest density scenario (9000), which is 50% less than FTP’s, because some vehicles choose to take the free of charge path rather than the paid congested roads, which helps to alleviate the congestion and shorten the vehicle’s travel time, thus reducing the average AT.

In Figure 7, the AD of the three schemes in different density scenarios is presented. In the low-density scenarios (under 750), the AD of the three schemes is negligible, but in the medium- and high-density scenarios, FTP’s and APT’s AD increase moderately to reach 1.6 at the highest density, because the alternative free paths are usually longer than the shortest path. However, DFT has no AD even in very high-density scenarios, because the shortest path is always taken. Some could argue that DFT is preferable since it has no AD. It is true that the distance in DFT is optimum and the vehicle does not have to travel additional distances to avoid the congestion, nonetheless, this comes at the cost of the enormous increase in the travel time, as shown in Figure 6. In other words, in our proposed system, there is an increase in terms of additional distance because some of the vehicles are willing to drive an additional distance and arrive early, for example, some prefer to drive an additional 2 KM and arrive in 15 minutes, rather than travel 1 KM and arrive in 30 minutes and pay T-Coins.

In Figure 6 and Figure 7, FPT and APT have almost the same performance, however, Figure 8 shows the superiority of our proposed scheme APT. In the low-density scenarios (up to 1200) the T-Coin gain of the three schemes is almost negligible, that is, due to the low traffic at the roads, the paid traffic quota is never reached; however, in the medium-density traffic scenarios (3000 to 5000), the T-Coin gain of the three schemes increases relative to the density increase, but at different rates. However, in the high-density scenarios (5000 to 9000), while DFT’s and FPT’s T-Coin gain stabilize at 450, that is, due to their static paid traffic quota. However, APT gain increases dramatically, due to its dynamic quota allocation and pricing. Figure 9 shows the additional traveled time by changing the percentage of drivers’ decisions to take the alternative free paths. From Figure 9, we can notice the negative correlation between the percentage of drivers’ decisions to take alternative free paths and the additional traveled time. This proves that the more drivers are willing to take the alternative path the shorter the average traveled time.

In addition to the comparison with T-Coin’s variants, we have also compared it with the following congestion alleviation systems, DIFTOS [22], SAINT [23], and DIVERT [25]. We have compared the simulated systems based on two metrics, the average travel time of all the simulated vehicles and the computational cost performed by the traffic center servers. Figure 10 shows the average travel time of each system in different traffic density settings. Throughout different traffic conditions, we observe that T-Coin has the shortest travel time as compared with the other systems, which is due to T-Coin’s alternative paths rerouting strategy. DIFTOS and DIVERT performs better than SAINT, due to their distributed architecture that allows updating the assigned routes frequently without contacting the central traffic server, which is the case with SAINT. Figure 11 shows the computational cost in the traffic center server for each system in different traffic conditions. Although T-Coin has the best performance in terms of computing cost and DIFTOS has the worst performance, it is worth mentioning that the computing in DIFTOS is distributed among many clusters of vehicular servers that are spread throughout the city map, unlike the case of SAINT and T-Coin where the traffic center server is centralized, and DIVERT that has a hybrid server architecture.

7. Conclusions

In this work, we have proposed a new congestion pricing system based on reward and punishment policies, where the vehicles are rewarded for voluntarily choosing to take an alternative path to alleviate the traffic congestion. The proposed system is implemented using vehicular ad hoc networks, which eliminate the need for installing a costly electronic toll collection system. We propose a new virtual currency called T-Coin (traffic coin), that is used to reward the vehicles for their positive attitude. T-Coin is also used in the tender between vehicles to manage the road reservation process. The proposed system uses dynamic pricing to adapt to peak-hour traffic congestions. Using simulated traffic on a real map of Beijing city, we have proven the usefulness of T-Coin as a traffic congestion pricing system. We have proven through extensive simulation that the proposed system reduces the travel time and encourages the drivers to take alternative non-congested paths.

However, the proposed system could be improved in many aspects, which we have left as future directions:

• In this work, we assumed the static management of the traffic lights, incorporating a dynamic traffic lights management system with T-Coin is one of our future directions.
• The proposed system has been proven to be efficiency in alleviating traffic congestion, however, the vehicle’s path represents very private information, if disclosed by a malicious node during the communication between the vehicle and the traffic control center. Therefore, an in-depth study of the security and privacy of the T-Coin system is one of our future directions.
• In the proposed system, the traffic control system is considered to be a centralized server. Changing the server model to a distributed vehicular server, where the server’s computational responsibility is performed by the vehicles themselves, is one of our future directions.