Periodic DFTB for Supported Clusters: Implementation and Application on Benzene Dimers Deposited on Graphene
Abstract
:1. Introduction
2. Methods
2.1. DFTB
- ; the atomic orbital energies of the isolated atom ;
- , which only depends on the distance between the two corresponding atomic centers: .
2.2. DFTB for Periodic Systems
3. Computational Details
3.1. DFTB Calculations
3.2. DFT Calculations
4. Benchmark Calculations: Graphene and Graphite
5. Graphene Supported Benzene and Benzene Dimers
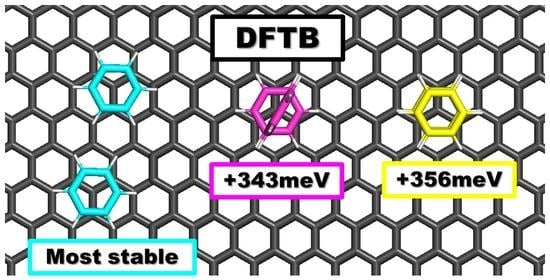
5.1. Benzene Supported on Graphene
5.2. Benzene Dimers in Vacuum
5.3. Benzene Dimers Supported on Graphene
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sadowska, M.; Cieśla, M.; Adamczyk, Z. Nanoparticle deposition on heterogeneous surfaces: Random sequential adsorption modeling and experiments. Colloids Surf. A Physicochem. Eng. Asp. 2021, 617, 126296. [Google Scholar] [CrossRef]
- Li, L.; Plessow, P.N.; Rieger, M.; Sauer, S.; Sánchez-Carrera, R.S.; Schaefer, A.; Abild-Pedersen, F. Modeling the migration of platinum nanoparticles on surfaces using a kinetic Monte Carlo approach. J. Phys. Chem. C 2017, 121, 4261–4269. [Google Scholar] [CrossRef]
- Rochefort, A.; Vernisse, L.; Gómez-Herrero, A.C.; Sánchez-Sánchez, C.; Martín-Gago, J.A.; Chérioux, F.; Clair, S.; Coraux, J.; Martínez, J.I. Role of the structure and reactivity of Cu and Ag surfaces in the formation of a 2D Metal–Hexahydroxytriphenylene network. J. Phys. Chem. C 2021, 125, 17333–17341. [Google Scholar] [CrossRef]
- Bruix, A.; Margraf, J.; Andersen, M.; Reuter, K. First-principles-based multiscale modelling of heterogeneous catalysis. Nat. Catal. 2019, 2, 659–670. [Google Scholar] [CrossRef]
- Abidi, N.; Lim, K.R.G.; Seh, Z.W.; Steinmann, S.N. Atomistic modeling of electrocatalysis: Are we there yet? WIREs Comput. Mol. Sci. 2021, 11, e1499. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, G.; Si, Y.; Liu, M. Surface modeling of photocatalytic materials for water splitting. Phys. Chem. Chem. Phys. 2022, 24, 1237–1261. [Google Scholar] [CrossRef] [PubMed]
- Vilan, A.; Cahen, D. Chemical modification of semiconductor surfaces for molecular electronics. Chem. Rev. 2017, 117, 4624–4666. [Google Scholar] [CrossRef] [PubMed]
- Shahmoradi, A.; Ahangari, M.G.; Jahanshahi, M.; Mirghoreishi, M.; Fathi, E.; Mashhadzadeh, A.H. Removal of methylmercaptan pollution using Ni and Pt-decorated graphene: An ab-initio DFT study. J. Sulfur Chem. 2020, 41, 593–604. [Google Scholar] [CrossRef]
- Li, M.; Zhu, H.; Wei, G.; He, A.; Liu, Y. DFT calculation and analysis of the gas sensing mechanism of methoxy propanol on Ag decorated SnO2 (110) surface. RSC Adv. 2019, 9, 35862–35871. [Google Scholar] [CrossRef] [Green Version]
- Soini, T.M.; Rösch, N. Size-dependent properties of transition metal clusters: From molecules to crystals and surfaces–computational studies with the program ParaGauss. Phys. Chem. Chem. Phys. 2015, 17, 28463–28483. [Google Scholar] [CrossRef] [PubMed]
- Porezag, D.; Frauenheim, T.; Köhler, T.; Seifert, G.; Kaschner, R. Construction of tight-binding-like potentials on the basis of density-functional theory: Application to carbon. Phys. Rev. B 1995, 51, 12947–12957. [Google Scholar] [CrossRef] [PubMed]
- Seifert, G.; Porezag, D.; Frauenheim, T. Calculations of molecules, clusters, and solids with a simplified LCAO-DFT-LDA scheme. Int. J. Quantum Chem. 1996, 58, 185–192. [Google Scholar] [CrossRef]
- Elstner, M.; Seifert, G. Density functional tight binding. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20120483. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spiegelman, F.; Tarrat, N.; Cuny, J.; Dontot, L.; Posenitskiy, E.; Martí, C.; Simon, A.; Rapacioli, M. Density-functional tight-binding: Basic concepts and applications to molecules and clusters. Adv. Phys. X 2020, 5, 1710252. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aradi, B.; Hourahine, B.; Frauenheim, T. DFTB+, a sparse matrix-based implementation of the DFTB method. J. Phys. Chem. A 2007, 111, 5678–5684. [Google Scholar] [CrossRef] [PubMed]
- Koskinen, P.; Makinen, V. Density-functional tight-binding for beginners. Comput. Mater. Sci. 2009, 47, 237–253. [Google Scholar] [CrossRef] [Green Version]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Walker, R.C.; Crowley, M.F.; Case, D.A. The implementation of a fast and accurate QM/MM potential method in Amber. J. Comput. Chem. 2008, 29, 1019–1031. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berendsen, H.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. cp2k: Atomistic simulations of condensed matter systems. WIREs Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef] [Green Version]
- Heine, T.; Rapacioli, M.; Patchkovskii, S.; Frenzel, J.; Koster, A.; Calaminici, P.; Duarte, H.A.; Escalante, S.; Flores-Moreno, R.; Goursot, A.; et al. deMonNano. 2009. Available online: http://demon-nano.ups-tlse.fr (accessed on 9 March 2022).
- Peeters, E.; Hony, S.; Van Kerckhoven, C.; Tielens, A.G.G.M.; Allamandola, L.J.; Hudgins, D.M.; Bauschlicher, C.W. The rich 6 to 9 μm spectrum of interstellar PAHs. Astron. Astrophys. 2002, 390, 1089–1113. [Google Scholar] [CrossRef] [Green Version]
- Rapacioli, M.; Joblin, C.; Boissel, P. Spectroscopy of polycyclic aromatic hydrocarbons and very small grains in photodissociation regions *. Astron. Astrophys. 2005, 429, 193–204. [Google Scholar] [CrossRef]
- Podeszwa, R.; Bukowski, R.; Szalewicz, K. Potential energy surface for the benzene dimer and perturbational analysis of pi-pi interactions. J. Phys. Chem. A 2006, 110, 10345–10354. [Google Scholar] [CrossRef] [PubMed]
- Rapacioli, M.; Spiegelman, F.; Talbi, D.; Mineva, T.; Goursot, A.; Heine, T.; Seifert, G. Correction for dispersion and coulombic interactions in molecular clusters with density functional derived methods: Application to polycyclic aromatic hydrocarbon clusters. J. Chem. Phys. 2009, 130, 244304. [Google Scholar] [CrossRef] [PubMed]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, H.; York, D.; Cui, Q.; Elstner, M. Extension of the self-consistent-charge density-functional tight-binding method: Third-order expansion of the density functional theory total energy and introduction of a modified effective coulomb interaction. J. Phys. Chem. A 2007, 111, 10861–10873. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhu, T.; Cramer, C.; Truhlar, D. New class IV charge model for extracting accurate partial charges from wave functions. J. Phys. Chem. A 1998, 102, 1820–1831. [Google Scholar] [CrossRef]
- Michoulier, E.; Ben Amor, N.; Rapacioli, M.; Noble, J.A.; Mascetti, J.; Toubin, C.; Simon, A. Theoretical determination of adsorption and ionisation energies of polycyclic aromatic hydrocarbons on water ice. Phys. Chem. Chem. Phys. 2018, 20, 11941–11953. [Google Scholar] [CrossRef]
- Dontot, L.; Spiegelman, F.; Zamith, S.; Rapacioli, M. Dependence upon charge of the vibrational spectra of small Polycyclic Aromatic Hydrocarbon clusters: The example of pyrene. Eur. Phys. J. D 2020, 74, 216. [Google Scholar] [CrossRef]
- Simon, A.; Rapacioli, M.; Michoulier, E.; Zheng, L.; Korchagina, K.; Cuny, J. Contribution of the density-functional-based tight-binding scheme to the description of water clusters: Methods, applications and extension to bulk systems. Mol. Simul. 2019, 45, 249–268. [Google Scholar] [CrossRef]
- Slater, J.C.; Koster, G.F. Simplified LCAO method for the meriodic motential mroblem. Phys. Rev. 1954, 94, 1498–1524. [Google Scholar] [CrossRef]
- Zhechkov, L.; Heine, T.; Patchkovskii, S.; Seifert, G.; Duarte, H.A. An efficient a posteriori treatment for dispersion interaction in density-functional-based tight binding. J. Chem. Theory Comput. 2005, 1, 841–847. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements. J. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for Ab Initio Total-Energy Calc. Using A Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Lebedeva, I.V.; Lebedev, A.V.; Popov, A.M.; Knizhnik, A.A. Comparison of performance of van der Waals-corrected exchange-correlation functionals for interlayer interaction in graphene and hexagonal boron nitride. Comput. Mater. Sci. 2017, 128, 45–58. [Google Scholar] [CrossRef] [Green Version]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, Y.X. Can all nitrogen-doped defects improve the performance of graphene anode materials for lithium-ion batteries? Phys. Chem. Chem. Phys. 2013, 15, 16819–16827. [Google Scholar] [CrossRef] [PubMed]
- Lebègue, S.; Harl, J.; Gould, T.; Ángyán, J.G.; Kresse, G.; Dobson, J.F. Cohesive properties and asymptotics of the dispersion interaction in graphite by the random phase approximation. Phys. Rev. Lett. 2010, 105, 196401. [Google Scholar] [CrossRef] [PubMed]
- Spanu, L.; Sorella, S.; Galli, G. Nature and strength of interlayer binding in graphite. Phys. Rev. Lett. 2009, 103, 196401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cooper, D.R.; D’Anjou, B.; Ghattamaneni, N.; Harack, B.; Hilke, M.; Horth, A.; Majlis, N.; Massicotte, M.; Vandsburger, L.; Whiteway, E.; et al. Experimental review of graphene. ISRN Condens. Matter Phys. 2012, 2012, 501686. [Google Scholar] [CrossRef] [Green Version]
- Bosak, A.; Krisch, M.; Mohr, M.; Maultzsch, J.; Thomsen, C. Elasticity of single-crystalline graphite: Inelastic x-ray scattering study. Phys. Rev. B 2007, 75, 153408. [Google Scholar] [CrossRef] [Green Version]
- Trucano, P.; Chen, R. Structure of graphite by neutron diffraction. Nature 1975, 258, 136–137. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Zhou, K.G.; Xie, K.F.; Zeng, J.; Zhang, H.L.; Peng, Y. Tuning the electronic structure and transport properties of graphene by noncovalent functionalization: Effects of organic donor, acceptor and metal atoms. Nanotechnology 2010, 21, 065201. [Google Scholar] [CrossRef]
- Berland, K.; Hyldgaard, P. Analysis of van der Waals density functional components: Binding and corrugation of benzene and C60 on boron nitride and graphene. Phys. Rev. B 2013, 87, 205421. [Google Scholar] [CrossRef] [Green Version]
- Ershova, O.V.; Lillestolen, T.C.; Bichoutskaia, E. Study of polycyclic aromatic hydrocarbons adsorbed on graphene using density functional theory with empirical dispersion correction. Phys. Chem. Chem. Phys. 2010, 12, 6483–6491. [Google Scholar] [CrossRef] [Green Version]
- Otyepková, E.; Lazar, P.; Čépe, K.; Tomanec, O.; Otyepka, M. Organic adsorbates have higher affinities to fluorographene than to graphene. Appl. Mater. Today 2016, 5, 142–149. [Google Scholar] [CrossRef] [Green Version]
- Zacharia, R.; Ulbricht, H.; Hertel, T. Interlayer cohesive energy of graphite from thermal desorption of polyaromatic hydrocarbons. Phys. Rev. B 2004, 69, 155406. [Google Scholar] [CrossRef] [Green Version]
- Rajesh, C.; Majumder, C.; Mizuseki, H.; Kawazoe, Y. A theoretical study on the interaction of aromatic amino acids with graphene and single walled carbon nanotube. J. Chem. Phys. 2009, 130, 124911. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.X. A dispersion-corrected DFT study on adsorption of battery active materials anthraquinone and its derivatives on monolayer graphene and h-BN. J. Mater. Chem. A 2014, 2, 8910–8917. [Google Scholar] [CrossRef]
- Yu, Y.X. Binding energy and work function of organic electrode materials phenanthraquinone, pyromellitic dianhydride and their derivatives adsorbed on graphene. ACS Appl. Mater. Interfaces 2014, 6, 16267–16275. [Google Scholar] [CrossRef] [PubMed]
- Kratzer, P.; Neugebauer, J. The basics of electronic structure theory for periodic systems. Front. Chem. 2019, 7, 106. [Google Scholar] [CrossRef] [PubMed] [Green Version]


| Methods | d | d | d |
|---|---|---|---|
| DFTB-D1 ** | 1.430 ± 0.001 | 1.429 ± 0.001 | 3.383 ± 0.001 |
| DFTB-D2 | 1.426 ± 0.001 | 1.425 ± 0.001 | 3.131 ± 0.001 |
| DFTB-D1 ** | 1.421 [34] | 1.421 [34] | 3.38 [34] |
| DFT-D3 | 1.425 ± 0.001 | 1.424 ± 0.001 | 3.488 ± 0.001 |
| PW91-OBS | 1.4226 [43] | ||
| RPA | 1.42 * [44] | 3.34 * [44] | |
| QMC | 1.42 * [45] | 3.426 * [45] | |
| Expt | 1.42 [46] | 1.422 [47,48] | 3.356 [47,48] |
| Method | a1 | a2 | a3 | a4 |
|---|---|---|---|---|
| DFTB-D1 | −0.639 | −0.652 | −0.654 | −0.651 |
| DFTB-D2 | −0.439 | −0.448 | −0.447 | −0.451 |
| DFT-D3 | −0.428 | −0.450 | −0.453 | −0.450 |
| LDA [49] | −0.16 | −0.23 | −0.24 | |
| B97X-D [51] | −0.47 | |||
| optB86b-vdw [52] | −0.5 | |||
| vdW-DF1 [50] | −0.49 | |||
| vdW-DF2 [50] | −0.43 | |||
| Expt. Saturated Adsorption Enthalpy [52] | −0.5 |
| Method | a1 | a2 | a3 | a4 |
|---|---|---|---|---|
| DFTB-D1 | 3.15 | 3.13 | 3.13 | 3.14 |
| DFTB-D2 | 3.08 | 3.07 | 3.08 | 3.05 |
| DFT-D3 | 3.47 | 3.38 | 3.36 | 3.42 |
| B97X-D [51] | 3.36 | 3.30 | 3.35 | |
| vdW-DF1 [50] | 3.6 | |||
| vdW-DF2 [50] | 3.5 | |||
| MP2 [54] | 3.33 |
| Method | T-Shaped | PD | SE | |
|---|---|---|---|---|
| DFTB-D1 | Csoa | −0.126 | −0.194 | −0.192 |
| DFTB-D1-WMull | Csoa | −0.140 | −0.162 | −0.148 |
| DFTB-D2 | T | −0.099 | −0.135 | −0.132 |
| DFTB-D2-WMull | T | −0.113 | −0.104 | −0.086 |
| DFT-D3 | Csoa | −0.146 | −0.152 | −0.106 |
| T | −0.138 | |||
| CCSD(T) [25] | Csoa | −0.12 | −0.12 | −0.07 |
| SAPT [25] | Csoa | −0.12 | −0.12 | −0.08 |
| DFTB-D2-WMull | DFT-D3 | |||||||
|---|---|---|---|---|---|---|---|---|
| T | PD * | SE | T | PD | SE | |||
| −0.586 | ↳ | −0.929 | −0.573 | −0.605 | −0.624 | −0.938 | −0.583 | |
| −0.473 | ↳ | - | −0.487 | −0.467 | −0.473 | - | −0.478 | |
| −0.135 | ↳ | −0.478 | −0.122 | −0.156 | −0.175 | −0.489 | −0.134 | |
| 0.316 | ↳ | −0.027 | 0.329 | 0.294 | 0.275 | −0.039 | 0.316 | |
| Z-separation | 3.03 | ↳ | 3.00 | 3.02/6.53 | 3.38 | 3.39/6.91 | 3.40/3.40 | 3.39/7.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rapacioli, M.; Tarrat, N. Periodic DFTB for Supported Clusters: Implementation and Application on Benzene Dimers Deposited on Graphene. Computation 2022, 10, 39. https://doi.org/10.3390/computation10030039
Rapacioli M, Tarrat N. Periodic DFTB for Supported Clusters: Implementation and Application on Benzene Dimers Deposited on Graphene. Computation. 2022; 10(3):39. https://doi.org/10.3390/computation10030039
Chicago/Turabian StyleRapacioli, Mathias, and Nathalie Tarrat. 2022. "Periodic DFTB for Supported Clusters: Implementation and Application on Benzene Dimers Deposited on Graphene" Computation 10, no. 3: 39. https://doi.org/10.3390/computation10030039
APA StyleRapacioli, M., & Tarrat, N. (2022). Periodic DFTB for Supported Clusters: Implementation and Application on Benzene Dimers Deposited on Graphene. Computation, 10(3), 39. https://doi.org/10.3390/computation10030039