CFD Simulation and Optimisation of a Low Energy Ventilation and Cooling System
Abstract
:1. Introduction
2. Previous Related Work
2.1. CFD Simulation of Wind Towers


2.2. CFD Simulation of Heat Transfer Devices

2.3. CFD Optimisation of Natural Ventilation Systems
3. CFD Methodology
3.1. Design Geometry


3.2. Mesh Generation and Verification

3.3. Boundary Conditions

3.4. Solution Convergence



4. Experimental Methodology



5. Results and Discussion
5.1. Validation of Computational Model

5.2. Airflow Distribution

5.3. Airflow Supply Rate
| Inlet Speed [m/s] | CFD Supply Rate [L/s] | CFD Supply Rate [L/s/occupant] | Building Regulation [L/s/occupant] | CFD [L/s/m2] Area = 25 m2 |
|---|---|---|---|---|
| 0.50 | 65.00 | 4.33 | 10.00 | 2.60 |
| 1.00 | 145.00 | 9.67 | 10.00 | 5.80 |
| 2.00 | 325.00 | 21.67 | 10.00 | 13.00 |
| 3.00 | 485.00 | 32.33 | 10.00 | 19.40 |
| 4.00 | 695.00 | 46.33 | 10.00 | 27.80 |
| 5.00 | 840.00 | 56.00 | 10.00 | 33.60 |
| Inlet Speed [m/s] | CFD Supply Rate [L/s] | CFD Supply Rate [L/s/occupant] | Building Regulation [L/s/occupant] | CFD [L/s/m2] Area = 25 m2 |
|---|---|---|---|---|
| 0.50 | 100.00 | 6.67 | 10.00 | 4.00 |
| 1.00 | 200.00 | 13.33 | 10.00 | 8.00 |
| 2.00 | 430.00 | 28.67 | 10.00 | 17.20 |
| 3.00 | 610.00 | 40.67 | 10.00 | 24.40 |
| 4.00 | 870.00 | 58.00 | 10.00 | 34.80 |
| 5.00 | 1090.00 | 72.67 | 10.00 | 43.60 |
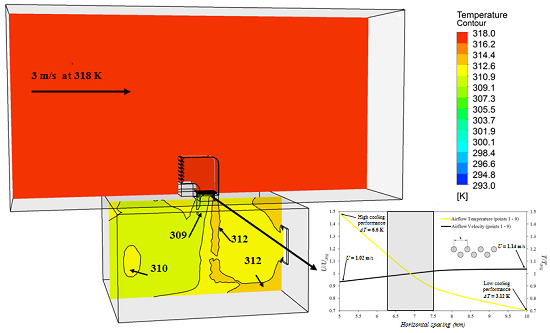
5.4. Temperature Distribution



5.5. Determining the Optimum Heat Transfer Device Spacing

6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bouchahm, Y.; Bourbia, F.; Belhamri, A. Performance analysis and improvement of the use of wind tower in hot dry climate. Renew. Energy 2011, 36, 898–906. [Google Scholar] [CrossRef]
- WBCSD. Energy Efficiency in Buildings: Facts & Trends; Atar Roto Presse: Satigny, Switzerland, 2008. [Google Scholar]
- Sofotasiou, P.; Hughes, B.R.; Calautit, J.K. Qatar 2022: Facing the FIFA World Cup climatic and legacy challenges. Sustain. Cities Soc. 2015, 14, 16–30. [Google Scholar] [CrossRef]
- Bahadori, M.N. Passive cooling systems in Iranian architecture. Sci. Am. 1978, 238, 144–154. [Google Scholar] [CrossRef]
- Hughes, B.R.; Calautit, J.K.; Ghani, S.A. The Development of Commercial Wind Towers for Natural Ventilation: A Review. Appl. Energy 2012, 92, 606–627. [Google Scholar] [CrossRef]
- O’Connor, D.; Calautit, J.K.; Hughes, B.R. A Study of Passive Ventilation Integrated with Heat Recovery. Energy Build. 2014, 82, 799–811. [Google Scholar] [CrossRef]
- Linden, P.F. The fluid mechanics of natural ventilation. Ann. Rev. Fluid Mech. 1999, 31, 201–238. [Google Scholar] [CrossRef]
- Bahadori, M.N. An improved design of wind towers for natural ventilation and passive cooling. Sol. Energy 1985, 35, 119–129. [Google Scholar] [CrossRef]
- Yaghoubi, M.A.; Sabzevari, A.; Golneshan, A.A. Wind Towers—Measurement and Performance. Sol. Energy 1991, 47, 97–106. [Google Scholar] [CrossRef]
- Hughes, B.R.; Mak, C.M. A study of wind and buoyancy driven flows through commercial wind towers. Energy Build. 2011, 43, 1784–1791. [Google Scholar] [CrossRef]
- Hughes, B.R.; Ghani, S.A. A numerical investigation into the effect of Windvent louvre external angle on passive stack ventilation performance. Build. Environ. 2010, 45, 1025–1036. [Google Scholar] [CrossRef]
- Liu, S.C.; Mak, C.M.; Niu, J.L. Numerical Evaluation of Louver Configuration and Ventilation Strategies for the Windcatcher System. Build. Environ. 2011, 46, 1600–1616. [Google Scholar] [CrossRef]
- Montazeri, H. Experimental and numerical study on natural ventilation performance of various multi-opening wind catchers. Build. Environ. 2011, 46, 370–378. [Google Scholar] [CrossRef]
- Calautit, J.K.; Chaudhry, H.N.; Hughes, B.R.; Ghani, S.A. Comparison between evaporative cooling and a heat pipe assisted thermal loop for a commercial wind tower in hot and dry climatic conditions. Appl. Energy 2013, 101, 740–755. [Google Scholar] [CrossRef]
- Gan, G.; Riffat, S.B. Naturally ventilated buildings with heat recovery: CFD simulation of thermal environment. Build. Serv. Eng. Res. Technol. 1997, 18, 67–75. [Google Scholar] [CrossRef]
- Hughes, B.R.; Chaudhry, H.N.; Calautit, J.K. Passive energy recovery from natural ventilation air streams. Appl. Energy 2014, 113, 127–140. [Google Scholar] [CrossRef]
- Calautit, J.K.; Hughes, B.R.; Chaudhry, H.N.; Ghani, S.A. CFD analysis of a heat transfer device integrated wind tower system for hot and dry climate. Appl. Energy 2013, 112, 576–591. [Google Scholar] [CrossRef]
- Stavrakakis, G.; Koukou, M.; Vrachopoulos, M.; Markatos, N. Natural cross-ventilation in buildings: Building-scale experiments, numerical simulation and thermal comfort evaluation. Energy Build. 2008, 40, 1666–1681. [Google Scholar] [CrossRef]
- Stavrakakis, G.; Zervas, P.; Sarimveis, H.; Markatos, N. Development of a computational tool to quantify architectural-design effects on thermal comfort in naturally ventilated rural houses. Build. Environ. 2010, 45, 65–80. [Google Scholar] [CrossRef]
- Zhou, L.; Haghighat, F. Optimization of ventilation system design and operation in office environment, Part I: Methodology. Building and Environment. Build. Environ. 2009, 44, 651–656. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, G.; Bjerg, B. Investigation of Response Surface Methodology for Modelling Ventilation Rate of a Naturally Ventilated Building. Build. Environ. 2012, 54, 174–185. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, G.; Bjerg, B. Assessments of Experimental Designs in Response Surface Modelling Process: Estimating Ventilation Rate in Naturally Ventilated Livestock Buildings. Energy Build. 2013, 62, 570–580. [Google Scholar] [CrossRef]
- Lal, S. Experimental, CFD simulation and parametric studies on modified solar chimney for building ventilation. Appl. Sol. Energy 2014, 50, 37–43. [Google Scholar] [CrossRef]
- Calautit, J.K.; O’Connor, D.; Hughes, B.R. Determining the optimum spacing and arrangement for commercial wind towers for ventilation performance. Build. Environ. 2014, 82, 274–287. [Google Scholar] [CrossRef]
- Yin, Y.; Xu, W.; Gupta, J.; Guity, A.; Marmion, P.; Manning, A.; Gulick, B.; Zhang, X.; Chen, Q. Experimental Study on Displacement and Mixing Ventilation Systems for a Patient Ward. HVAC&R Res. 2010, 15, 1175–1191. [Google Scholar] [CrossRef]
- Aliabadi, A.; Faghani, E.; Tjong, H.; Green, S. Hybrid Ventilation Design for a Dining Hall Using Computational Fluid Dynamics (CFD). In Proceedings of the CSME International Congress 2014, Toronto, ON, Canada, 2014.
- Chen, Q. Using computational tools to factor wind into architectural environment design. Energy Build. 2004, 36, 1197–1209. [Google Scholar] [CrossRef]
- ANSYS® Academic Research. ANSYS FLUENT User’s Guide Release 14.0. Available online: https://www.ansys.com (accessed on 1 January 2014).
- Calautit, J.K.; Hughes, B.R.; Ghani, S.A. A Numerical Investigation into the Feasibility of Integrating Green Building Technologies into Row Houses in the Middle East. Archit. Sci. Rev. 2013, 56, 279–296. [Google Scholar] [CrossRef]
- Calautit, J.K.; Hughes, B.R. Wind tunnel and CFD study of the natural ventilation performance of a commercial multi-directional wind tower. Build. Environ. 2014, 80, 71–83. [Google Scholar] [CrossRef]
- Calautit, J.K. Integration and Application of Passive Cooling within a Wind Tower. Ph.D. Thesis, University of Leeds, Leeds, UK, 2013. [Google Scholar]
- Calautit, J.K.; Hughes, B.R.; Ghani, S.A. Numerical investigation of the integration of heat transfer devices into wind towers. Chem. Eng. Trans. 2013, 34, 43–48. [Google Scholar]
- Chung, T. Computational Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Calautit, J.K.; Hughes, B.R. Measurement and prediction of the indoor airflow in a room ventilated with a commercial wind tower. Energy Build. 2014, 84, 367–377. [Google Scholar] [CrossRef]
- Calautit, J.K.; Hughes, B.R. Integration and application of passive cooling within a wind tower for hot climates. HVAC&R Res. 2014, 20, 722–730. [Google Scholar] [CrossRef]
- Calautit, J.K.; Chaudhry, H.N.; Hughes, B.R.; Sim, L.F. A validated design methodology for a closed-loop subsonic wind tunnel. J. Wind Eng. Ind. Aerodyn. 2014, 125, 180–194. [Google Scholar]
- Cermak, J.E.; Isyumov, N. Wind Tunnel Studies of Buildings and Structure; ASCE Publications: Virginia, USA, 1999. [Google Scholar]
- Linden, P.F.; Cooper, P. Multiple sources of buoyancy in a naturally ventilated enclosure. J. Fluid Mech. 1996, 311, 177–192. [Google Scholar] [CrossRef]
- Building Regulations 2000: Approved Document F1A: Means of Ventilation. Available online: https://www.planningportal.gov.uk (accessed on 1 January 2014).
- Seppänen, O.A.; Fisk, W.J.; Mendell, M.J. Association of ventilation rates and CO2 concentrations with health and other responses in commercial and institutional buildings. Indoor Air 1999, 9, 226–252. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calautit, J.K.; O'Connor, D.; Sofotasiou, P.; Hughes, B.R. CFD Simulation and Optimisation of a Low Energy Ventilation and Cooling System. Computation 2015, 3, 128-149. https://doi.org/10.3390/computation3020128
Calautit JK, O'Connor D, Sofotasiou P, Hughes BR. CFD Simulation and Optimisation of a Low Energy Ventilation and Cooling System. Computation. 2015; 3(2):128-149. https://doi.org/10.3390/computation3020128
Chicago/Turabian StyleCalautit, John Kaiser, Dominic O'Connor, Polytimi Sofotasiou, and Ben Richard Hughes. 2015. "CFD Simulation and Optimisation of a Low Energy Ventilation and Cooling System" Computation 3, no. 2: 128-149. https://doi.org/10.3390/computation3020128
APA StyleCalautit, J. K., O'Connor, D., Sofotasiou, P., & Hughes, B. R. (2015). CFD Simulation and Optimisation of a Low Energy Ventilation and Cooling System. Computation, 3(2), 128-149. https://doi.org/10.3390/computation3020128