Electron Density and Its Relation with Electronic and Optical Properties in 2D Mo/W Dichalcogenides
Abstract
:1. Introduction
2. Computational Details
3. 2D Multilayers
3.1. Stability, Electronic, and Optical Properties
3.2. Electron Density Analysis
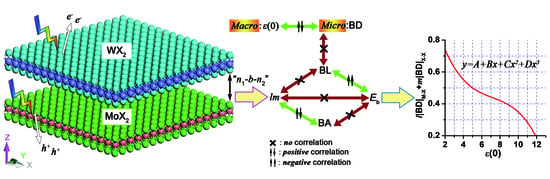
4. 2D Heterostructure
4.1. Stability, Electronic, and Optical Properties
4.2. Electron Density Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Novoselov, K.S. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jariwala, D.; Davoyan, A.R.; Wong, J.; Atwater, H.A. Van der Waals Materials for Atomically-Thin Photovoltaics: Promise and Outlook. ACS Photonics 2017, 4, 2962–2970. [Google Scholar] [CrossRef] [Green Version]
- Brahma, M.; Kabiraj, A.; Saha, D.; Mahapatra, S. Scalability assessment of Group-IV mono-chalcogenide based tunnel FET. Sci. Rep. 2018, 8, 5993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chhowalla, M.; Shin, H.S.; Eda, G.; Li, L.-J.; Loh, K.P.; Zhang, H. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 2013, 5, 263–275. [Google Scholar] [CrossRef] [PubMed]
- Lukowski, M.A.; Daniel, A.S.; Meng, F.; Forticaux, A.; Li, L.; Jin, S. Enhanced Hydrogen Evolution Catalysis from Chemically Exfoliated Metallic MoS 2 Nanosheets. J. Am. Chem. Soc. 2013, 135, 10274–10277. [Google Scholar] [CrossRef] [PubMed]
- Long, M.; Wang, P.; Fang, H.; Hu, W. Progress, Challenges, and Opportunities for 2D Material Based Photodetectors. Adv. Funct. Mater. 2019, 29, 1803807. [Google Scholar] [CrossRef]
- Xu, M.; Liang, T.; Shi, M.; Chen, H. Graphene-Like Two-Dimensional Materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef]
- Wu, F.; Li, Q.; Wang, P.; Xia, H.; Wang, Z.; Wang, Y.; Luo, M.; Chen, L.; Chen, F.; Miao, J.; et al. High efficiency and fast van der Waals hetero-photodiodes with a unilateral depletion region. Nat. Commun. 2019, 10, 4663. [Google Scholar] [CrossRef] [Green Version]
- Tan, C.; Lai, Z.; Zhang, H. Ultrathin two-dimensional multinary layered metal chalcogenide nanomaterials. Adv. Mater. 2017, 29, 1701392. [Google Scholar] [CrossRef]
- Jariwala, D.; Marks, T.J.; Hersam, M.C. Mixed-dimensional van der Waals heterostructures. Nat. Mater. 2017, 16, 170–181. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H. Electronic band structures of Molybdenum and Tungsten dichalcogenides by the GW approach. J. Phys. Chem. C 2012, 116, 7664–7671. [Google Scholar] [CrossRef]
- Wang, S.; Tian, H.; Ren, C.; Yu, J.; Sun, M. Electronic and optical properties of heterostructures based on transition metal dichalcogenides and graphene-like zinc oxide. Sci. Rep. 2018, 8, 12009. [Google Scholar] [CrossRef] [PubMed]
- Py, M.A.; Haering, R.R. Structural destabilization induced by lithium intercalation in MoS 2 and related compounds. Can. J. Phys. 1983, 61, 76–84. [Google Scholar] [CrossRef]
- Huang, H.H.; Fan, X.; Singh, D.J.; Chen, H.; Jiang, Q.; Zheng, W.T. Controlling phase transition for single-layer MTe2 (M = Mo and W): modulation of the potential barrier under strain. Phys. Chem. Chem. Phys. 2016, 18, 4086–4094. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Medhekar, N.V.; Shenoy, V.B. Bonding Charge Density and Ultimate Strength of Monolayer Transition Metal Dichalcogenides. J. Phys. Chem. C 2013, 117, 15842–15848. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.-F.; Zeng, Z. Roles of Mass, Structure, and Bond Strength in the Phonon Properties and Lattice Anharmonicity of Single-Layer Mo and W Dichalcogenides. J. Phys. Chem. C 2015, 119, 18779–18789. [Google Scholar] [CrossRef]
- Voiry, D.; Mohite, A.; Chhowalla, M. Phase engineering of transition metal dichalcogenides. Chem. Soc. Rev. 2015, 44, 2702–2712. [Google Scholar] [CrossRef]
- Wilson, J.A.; Yoffe, A.D. The transition metal dichalcogenides discussion and interpretation of the observed optical, electrical and structural properties. Adv. Phys. 1969, 18, 193–335. [Google Scholar] [CrossRef]
- Heising, J.; Kanatzidis, M.G. Exfoliated and Restacked MoS2 and WS2: Ionic or Neutral Species? Encapsulation and Ordering of Hard Electropositive Cations. J. Am. Chem. Soc. 1999, 121, 11720–11732. [Google Scholar] [CrossRef]
- Eda, G.; Fujita, T.; Yamaguchi, H.; Voiry, D.; Chen, M.; Chhowalla, M. Coherent Atomic and Electronic Heterostructures of Single-Layer MoS2. ACS Nano 2012, 6, 7311–7317. [Google Scholar] [CrossRef]
- Cheng, X.; Li, Y.; Shang, J.; Hu, C.; Ren, Y.; Liu, M.; Qi, Z. Thickness-dependent phase transition and optical behavior of MoS2 films under high pressure. Nano Res. 2018, 11, 855–863. [Google Scholar] [CrossRef]
- Kumar, A.; Ahluwalia, P.K. Electronic structure of transition metal dichalcogenides monolayers 1H-MX2 (M = Mo, W; X = S, Se, Te) from ab-initio theory: new direct band gap semiconductors. Eur. Phys. J. B 2012, 85, 186. [Google Scholar] [CrossRef]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically Thin MoS 2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [Green Version]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Kim, J.; Chim, C.-Y.; Galli, G.; Wang, F. Emerging Photoluminescence in Monolayer MoS 2. Nano Lett. 2010, 10, 1271–1275. [Google Scholar] [CrossRef]
- Ruppert, C.; Aslan, O.B.; Heinz, T.F. Optical properties and band gap of single- and few-layer MoTe2 crystals. Nano Lett. 2014, 14, 6231–6236. [Google Scholar] [CrossRef]
- Latzke, D.W.; Zhang, W.; Suslu, A.; Chang, T.-R.; Lin, H.; Jeng, H.-T.; Tongay, S.; Wu, J.; Bansil, A.; Lanzara, A. Electronic structure, spin-orbit coupling, and interlayer interaction in bulk MoS 2 and WS 2. Phys. Rev. B 2015, 91, 235202. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.; Lin, J.; Wang, X.; Shi, G.; Lei, S.; Lin, Z.; Zou, X.; Ye, G.; Vajtai, R.; Yakobson, B.I.; et al. Vertical and in-plane heterostructures from WS2/MoS2 monolayers. Nat. Mater. 2014, 13, 1135–1142. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Wu, S.; Sanchez, A.M.; Peters, J.J.P.; Beanland, R.; Ross, J.S.; Rivera, P.; Yao, W.; Cobden, D.H.; Xu, X. Lateral heterojunctions within monolayer MoSe2–WSe2 semiconductors. Nat. Mater. 2014, 13, 1096–1101. [Google Scholar] [CrossRef]
- Lee, C.-H.; Lee, G.-H.; van der Zande, A.M.; Chen, W.; Li, Y.; Han, M.; Cui, X.; Arefe, G.; Nuckolls, C.; Heinz, T.F.; et al. Atomically thin p–n junctions with van der Waals heterointerfaces. Nat. Nanotechnol. 2014, 9, 676–681. [Google Scholar] [CrossRef] [Green Version]
- Amin, B.; Singh, N.; Schwingenschlögl, U. Heterostructures of transition metal dichalcogenides. Phys. Rev. B 2015, 92, 075439. [Google Scholar] [CrossRef] [Green Version]
- Kahn, E.; Liu, M.; Zhang, T.; Liu, H.; Fujisawa, K.; Bepete, G.; Ajayan, P.M.; Terrones, M. Functional hetero-interfaces in atomically thin materials. Mater. Today 2020, 37, 74–92. [Google Scholar] [CrossRef]
- Gupta, A.; Sakthivel, T.; Seal, S. Recent development in 2D materials beyond graphene. Prog. Mater. Sci. 2015, 73, 44–126. [Google Scholar] [CrossRef]
- Wang, X.; Sun, Y.; Liu, K. Chemical and structural stability of 2D layered materials. 2D Mater. 2019, 6, 042001. [Google Scholar] [CrossRef]
- Li, J.; Huang, L.; Hou, J.; Wu, X.; Niu, J.; Chen, G.; Gong, J.; Kong, Y.; Xiao, X. Effects of substrate orientation and solution movement in chemical bath deposition on Zn(O,S) buffer layer and Cu(In,Ga)Se2 thin film solar cells. Nano Energy 2019, 58, 427–436. [Google Scholar] [CrossRef]
- Luo, Z.; Ouyang, Y.; Zhang, H.; Xiao, M.; Ge, J.; Jiang, Z.; Wang, J.; Tang, D.; Cao, X.; Liu, C.; et al. Chemically activating MoS2 via spontaneous atomic palladium interfacial doping towards efficient hydrogen evolution. Nat. Commun. 2018, 9, 2120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Zhou, F.; Zhang, S.; Liang, Y.; Wang, R. Engineering MoS 2 Basal Planes for Hydrogen Evolution via Synergistic Ruthenium Doping and Nanocarbon Hybridization. Adv. Sci. 2019, 6, 1900090. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, D.; Ye, K.; Moses, O.A.; Xu, W.; Liu, D.; Song, P.; Wu, C.; Wang, C.; Ding, S.; Chen, S.; et al. Engineering the In-Plane Structure of Metallic Phase Molybdenum Disulfide via Co and O Dopants toward Efficient Alkaline Hydrogen Evolution. ACS Nano 2019, 13, 11733–11740. [Google Scholar] [CrossRef] [PubMed]
- Su, L.; Yu, Y.; Cao, L.; Zhang, Y. Effects of substrate type and material-substrate bonding on high-temperature behavior of monolayer WS2. Nano Res. 2015, 8, 2686–2697. [Google Scholar] [CrossRef]
- Ghorbani-Asl, M.; Zibouche, N.; Wahiduzzaman, M.; Oliveira, A.F.; Kuc, A.; Heine, T. Electromechanics in MoS2 and WS2: nanotubes vs. monolayers. Sci. Rep. 2013, 3, 2961. [Google Scholar] [CrossRef] [Green Version]
- Kou, L.; Frauenheim, T.; Chen, C. Nanoscale Multilayer Transition-Metal Dichalcogenide Heterostructures: Band Gap Modulation by Interfacial Strain and Spontaneous Polarization. J. Phys. Chem. Lett. 2013, 4, 1730–1736. [Google Scholar] [CrossRef]
- Zhao, Y.-H.; Yang, F.; Wang, J.; Guo, H.; Ji, W. Continuously tunable electronic structure of transition metal dichalcogenides superlattices. Sci. Rep. 2015, 5, 8356. [Google Scholar] [CrossRef] [Green Version]
- Klimeš, J.; Bowler, D.R.; Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 2009, 22, 022201. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Tang, H.; Shahi, C. Origin of the size-dependence of the equilibrium van der Waals binding between nanostructures. J. Chem. Phys. 2018, 148, 074110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, G.-X.; Tkatchenko, A.; Paier, J.; Appel, H.; Scheffler, M. van der Waals interactions in ionic and semiconductor solids. Phys. Rev. Lett. 2011, 107, 245501. [Google Scholar] [CrossRef] [Green Version]
- Ci, P.; Chen, Y.; Kang, J.; Suzuki, R.; Choe, H.S.; Suh, J.; Ko, C.; Park, T.; Shen, K.; Iwasa, Y.; et al. Quantifying van der Waals Interactions in Layered Transition Metal Dichalcogenides from Pressure-Enhanced Valence Band Splitting. Nano Lett. 2017, 17, 4982–4988. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X–H F–Y systems. J. Chem. Phys. 2002, 117, 5529–5542. [Google Scholar] [CrossRef]
- Mitroy, J.; Safronova, M.S.; Clark, C.W. Theory and applications of atomic and ionic polarizabilities. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 202001. [Google Scholar] [CrossRef]
- Atkins, P.W.; De Paula, J. Atkins’ Physical Chemistry, 9th ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 2010; ISBN 978-0-19-954337-3. [Google Scholar]
- Morita, K.; Davies, D.W.; Butler, K.T.; Walsh, A. Modeling the dielectric constants of crystals using machine learning. J. Chem. Phys. 2020, 153, 024503. [Google Scholar] [CrossRef]
- Hu, X.; Kou, L.; Sun, L. Stacking orders induced direct band gap in bilayer MoSe2-WSe2 lateral heterostructures. Sci. Rep. 2016, 6, 31122. [Google Scholar] [CrossRef] [Green Version]
- Terrones, H.; López-Urías, F.; Terrones, M. Novel hetero-layered materials with tunable direct band gaps by sandwiching different metal disulfides and diselenides. Sci. Rep. 2013, 3, 1549. [Google Scholar] [CrossRef]
- Wang, F.; Wang, J.; Guo, S.; Zhang, J.; Hu, Z.; Chu, J. Tuning coupling behavior of stacked heterostructures based on MoS2, WS2, and WSe2. Sci. Rep. 2017, 7, 44712. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J. WIEN2k: An Augmented Plane Wave Local Orbitals Program for Calculating Crystal Properties; Karlheinz Schwarz; Technische Universität Wien: Vienna, Austria, 2001; ISBN 3-9501031-1-2. [Google Scholar]
- Wu, Z.; Cohen, R.E. More accurate generalized gradient approximation for solids. Phys. Rev. B 2006, 73, 235116. [Google Scholar] [CrossRef] [Green Version]
- Tran, F.; Blaha, P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Zeng, F.; Zhang, W.-B.; Tang, B.-Y. Electronic structures and elastic properties of monolayer and bilayer transition metal dichalcogenides MX 2 ( M = Mo, W; X = O, S, Se, Te): A comparative first-principles study. Chin. Phys. B 2015, 24, 097103. [Google Scholar] [CrossRef] [Green Version]
- Otero-de-la-Roza, A.; Johnson, E.R.; Luaña, V. Critic2: A program for real-space analysis of quantum chemical interactions in solids. Comput. Phys. Commun. 2014, 185, 1007–1018. [Google Scholar] [CrossRef]
- Jiang, P.; Boulet, P.; Record, M.-C. A DFT study of the electronic, optical and topological properties of free and biaxially strained CuIn1−xAlxSe2. J. Mater. Chem. C 2019, 7, 5803–5815. [Google Scholar] [CrossRef]
- Jiang, P.; Record, M.-C.; Boulet, P. First-principles calculations on CuInSe2/AlP heterostructures. J. Mater. Chem. C 2020, 8, 4732–4742. [Google Scholar] [CrossRef]
- Gusakova, J.; Wang, X.; Shiau, L.L.; Krivosheeva, A.; Shaposhnikov, V.; Borisenko, V.; Gusakov, V.; Tay, B.K. Electronic Properties of Bulk and Monolayer TMDs: Theoretical Study Within DFT Framework (GVJ-2e Method). Phys. Status Solidi A 2017, 214, 1700218. [Google Scholar] [CrossRef]
- Yang, H.; Boulet, P.; Record, M.-C. A rapid method for analyzing the chemical bond from energy densities calculations at the bond critical point. Comput. Theor. Chem. 2020, 1178, 112784. [Google Scholar] [CrossRef]
- Gatti, C. Chemical bonding in crystals: new directions. Z. Für Krist. - Cryst. Mater. 2005, 220. [Google Scholar] [CrossRef]
- Kowalczyk, S.P.; Cheung, J.T.; Kraut, E.A.; Grant, R.W. CdTe-HgTe (-1-1-1) heterojunction valence-band discontinuity: A common-anion-rule contradiction. Phys. Rev. Lett. 1986, 56, 1605–1608. [Google Scholar] [CrossRef]
- Kang, J.; Tongay, S.; Zhou, J.; Li, J.; Wu, J. Band offsets and heterostructures of two-dimensional semiconductors. Appl. Phys. Lett. 2013, 102, 012111. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Zunger, A. Identification of potential photovoltaic absorbers based on first-principles spectroscopic screening of materials. Phys. Rev. Lett. 2012, 108, 068701. [Google Scholar] [CrossRef]












| Equation Order | R2 | AIC | BIC | A | B | C | D | |
|---|---|---|---|---|---|---|---|---|
| [MX2]n=1 | 1st | 0.685 | −36.76 | −37.17 | −2.59 × 10−2 | 3.39 × 10−1 | ||
| 2nd | 0.974 | −49.68 | −50.3 | 3.26 × 10−2 | 1.78 × 10−1 | −3.32 × 10−2 | ||
| 3rd | 0.999 | −67.74 | −68.58 | 1.07 × 100 | −8.54 × 10−1 | 3.04 × 10−1 | −3.61 × 10−2 | |
| [MX2]n=2 | 1st | 0.917 | −29.4 | −29.82 | −4.66 × 10−2 | 5.56 × 10−1 | ||
| 2nd | 0.993 | −44.34 | −44.96 | 1.63 × 10−1 | 1.32 × 10−1 | −1.96 × 10−1 | ||
| 3rd | 0.996 | −56.68 | −57.51 | 8.75 × 10−1 | −3.69 × 10−1 | 9.45 × 10−2 | −8.46 × 10−3 | |
| [MX2]n=3 | 1st | 0.823 | −21.89 | −22.31 | −5.90 × 10-2 | 4.71 × 10−1 | ||
| 2nd | 0.882 | −22.84 | −23.46 | 7.91 × 10−2 | 9.25 × 10−2 | −1.40 × 10−2 | ||
| 3rd | 0.999 | −60.44 | −61.27 | 1.85 × 100 | −5.47 × 10−1 | 9.55 × 10−2 | −6.10 × 10−3 | |
| Bulk | 1st | 0.870 | −27.53 | −27.94 | −2.76 × 10−2 | 3.81 × 10−1 | ||
| 2nd | 0.948 | −27.36 | −27.98 | 7.98 × 10−1 | −9.49 × 10−3 | −1.66 × 10−3 | ||
| 3rd | 0.999 | −54.23 | −55.06 | 1.09 × 100 | −2.30 × 10−1 | 2.89 × 10−2 | −1.34 × 10−3 | |
| WX2/MoX2 | 1st | 0.876 | −102.3 | −100.3 | −5.46 × 10−2 | 5.63 × 10−1 | ||
| 2nd | 0.900 | −104.9 | −101.9 | 3.87 × 10−1 | 2.40 × 10−2 | −8.45 × 10−3 | ||
| 3rd | 0.940 | −114.7 | −110.7 | −5.82 × 10−1 | 6.98 × 10−1 | −1.60 × 10−1 | 3.03 × 10−3 |
| WX2/MoX2 | N° | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| lm | 0.06 | 1.96 | 5.30 | 1.88 | 0.02 | 3.36 | 5.19 | 3.30 | 0.04 | |
| Top [WX2]n=2 | X | S | Se | Te | S | Se | Te | S | Se | Te |
| N° | 1′ | 2′ | 3′ | 4′ | 5′ | 6′ | 7′ | 8′ | 9′ | |
| Sign | - | - | - | + | - | - | + | + | - | |
| Bottom [MoX2]n=2 | X | S | S | S | Se | Se | Se | Te | Te | Te |
| N° | 1′’ | 2′’ | 3′’ | 4′’ | 5′’ | 6′’ | 7′’ | 8′’ | 9′’ | |
| sign | + | + | + | - | + | + | - | - | + |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, P.; Record, M.-C.; Boulet, P. Electron Density and Its Relation with Electronic and Optical Properties in 2D Mo/W Dichalcogenides. Nanomaterials 2020, 10, 2221. https://doi.org/10.3390/nano10112221
Jiang P, Record M-C, Boulet P. Electron Density and Its Relation with Electronic and Optical Properties in 2D Mo/W Dichalcogenides. Nanomaterials. 2020; 10(11):2221. https://doi.org/10.3390/nano10112221
Chicago/Turabian StyleJiang, Pingping, Marie-Christine Record, and Pascal Boulet. 2020. "Electron Density and Its Relation with Electronic and Optical Properties in 2D Mo/W Dichalcogenides" Nanomaterials 10, no. 11: 2221. https://doi.org/10.3390/nano10112221
APA StyleJiang, P., Record, M. -C., & Boulet, P. (2020). Electron Density and Its Relation with Electronic and Optical Properties in 2D Mo/W Dichalcogenides. Nanomaterials, 10(11), 2221. https://doi.org/10.3390/nano10112221