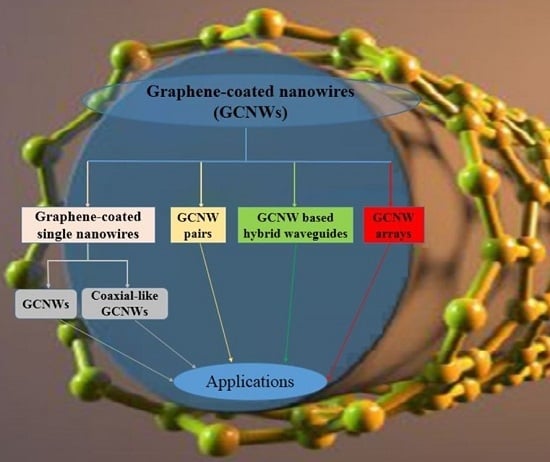
Graphene-Coated Nanowire Waveguides and Their Applications
Abstract
:1. Introduction
2. Surface Conductivity of Graphene
3. GCNW Waveguides
3.1. Graphene-Coated Single Nanowires
3.1.1. GCNWs
3.1.2. Coaxial-like GCNWs
3.2. GCNW Pairs
3.3. GCNW-Based Hybrid Waveguides
3.4. GCNW Arrays
4. Applications of GCNWs
4.1. Photonic Devices
4.2. Ultrafast Optical Modulators
4.3. Nonlinear Optics
4.3.1. Saturable Absorber in Fiber Lasers
4.3.2. Optical Bistability
4.3.3. Other Nonlinear Effects
4.4. Optical Cloaking
4.5. Other Applications
5. Conclusions and Perspective
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GCNWs | Graphene-coated nanowires |
| THz | Terahertz |
| SPs | Surface plasmons |
| 1/2/3D | One/two/three-dimensional |
| TM | Transverse-magnetic |
| TE | Transverse-electric |
| FWHM | Full width at half maximum |
| RGO | Reduced graphene oxide |
| Neff | Effective mode index |
| f0 | Frequency |
| λ0 | Wavelength in vacuum |
| μc | Chemical potential of graphene |
| LP | Propagation length |
| R | Radius of dielectric nanowire |
| εd | Permittivity of dielectric nanowire |
References
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef]
- Ozbay, E. Plasmonics: Merging photonics and electronics at nanoscale dimensions. Science 2006, 311, 189–193. [Google Scholar] [CrossRef] [PubMed]
- Zayats, A.V.; Smolyaninov, I.I.; Maradudin, A.A. Nano-optics of surface plasmon polaritons. Phys. Rep. 2005, 408, 131–314. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Sorger, V.J.; Oulton, R.F.; Ma, R.M.; Zhang, X. Toward integrated plasmonic circuits. MRS Bull. 2012, 37, 728–738. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.T.; Choi, S.Y. Graphene-based plasmonic waveguides for photonic integrated circuits. Opt. Express 2011, 19, 24557–24562. [Google Scholar] [CrossRef]
- Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; Van Duyne, R.P. Biosensing with plasmonic nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef]
- Ma, R.M.; Oulton, R.F.; Sorger, V.J.; Zhang, X. Plasmon lasers: Coherent light source at molecular scales. Laser Photonics Rev. 2012, 7, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Koppens, F.H.L.; Chang, D.E.; García de Abajo, F.J. Graphene plasmonics: A platform for strong light–matter interactions. Nano Lett. 2011, 11, 3370–3377. [Google Scholar] [CrossRef] [Green Version]
- Argyropoulos, C. Enhanced transmission modulation based on dielectric metasurfaces loaded with graphene. Opt. Express 2015, 23, 23787–23797. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vakil, A.; Engheta, N. Transformation optics using graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dai, Y.; Zhu, X.; Mortensen, N.A.; Zi, J.; Xiao, S. Nanofocusing in a tapered graphene plasmonic waveguide. J. Opt. 2015, 17, 065002. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Zhang, X.; Ma, Z.; Cai, W.; Wang, L.; Xu, J. Surface plasmon modes in graphene wedge and groove waveguides. Opt. Express 2013, 21, 32432–32440. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zhu, Y.Y.; Zhang, K.; Wu, H.W.; Peng, R.W.; Fan, R.H.; Wang, M. Plasmonic band structures in doped graphene tubes. Opt. Express 2017, 25, 12081–12089. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zeng, Y.; Xu, X.; Chen, X.; Zhou, Z.; Shi, P.; Yi, Z.; Ye, X.; Xiao, S.; Yi, Y. Plasmonic absorption enhancement in elliptical graphene arrays. Nanomaterials 2018, 8, 175. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Guan, X.; Zhu, X.; Hu, H.; Bozhevolnyi, S.I.; Oxenløwe, L.K.; Jin, K.J.; Mortensen, N.A.; Xiao, S. Efficient electro-optic modulation in low-loss graphene-plasmonic slot waveguides. Nanoscale 2017, 9, 15576–15581. [Google Scholar] [CrossRef] [Green Version]
- Gonçalves, P.A.D.; Dias, E.J.C.; Xiao, S.; Vasilevskiy, M.I.; Mortensen, N.A.; Peres, N.M.R. Graphene plasmons in triangular wedges and grooves. ACS Photonics 2016, 3, 2176–2183. [Google Scholar] [CrossRef] [Green Version]
- Jabbarzadeh, F.; Habibzadeh-Sharif, A. Double V-groove dielectric loaded plasmonic waveguide for sensing applications. J. Opt. Soc. Am. B 2019, 36, 690–696. [Google Scholar] [CrossRef]
- Ansell, D.; Radko, I.P.; Han, Z.; Rodriguez, F.J.; Bozhevolnyi, S.I.; Grigorenko, A.N. Hybrid graphene plasmonic waveguide modulators. Nat. Commun. 2015, 6, 8846. [Google Scholar] [CrossRef]
- Hao, R.; Jiao, J.; Peng, X.; Zhen, Z.; Dagarbek, R.; Zou, Y.; Li, E. Experimental demonstration of a graphene-based hybrid plasmonic modulator. Opt. Lett. 2019, 44, 2586–2589. [Google Scholar] [CrossRef] [PubMed]
- Gubin, M.Y.; Leksin, A.Y.; Shesterikov, A.V.; Prokhorov, A.V.; Volkov, V.S. All-plasmonic switching effect in the graphene nanostructures containing quantum emitters. Nanomaterials 2020, 10, 122. [Google Scholar] [CrossRef] [Green Version]
- Ono, M.; Hata, M.; Tsunekawa, M.; Nozaki, K.; Sumikura, H.; Chiba, H.; Notomi, M. Ultrafast and energy-efficient all-optical switching with graphene-loaded deep-subwavelength plasmonic waveguides. Nat. Photonics 2020, 14, 37–43. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Nie, X.; Shen, F.; Zhou, H.; Zhou, Q.; Gao, J.; Guo, K. Actively tunable terahertz switches based on subwavelength graphene waveguide. Nanomaterials 2018, 8, 665. [Google Scholar] [CrossRef] [PubMed]
- Pei, C.; Yang, L.; Wang, G.; Wang, Y.; Jiang, X.; Hao, Y.; Li, Y.; Yang, J. Broadband graphene/glass hybrid waveguide polarizer. IEEE Photonics Technol. Lett. 2015, 27, 927–930. [Google Scholar] [CrossRef]
- Hu, X.; Wang, J. Ultrabroadband compact graphene–silicon TM-pass polarizer. IEEE Photon. J. 2017, 9, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Wu, D.; Tian, J.; Li, L.; Yang, R. Plasmon induced transparency and refractive index sensing in a new type of graphene-based plasmonic waveguide. Opt. Commun. 2018, 412, 41–48. [Google Scholar] [CrossRef]
- Luongo, G.; Giubileo, F.; Genovese, L.; Iemmo, L.; Martucciello, N.; Di Bartolomeo, A. I-V and C-V Characterization of a High-Responsivity Graphene/Silicon Photodiode with Embedded MOS Capacitor. Nanomaterials 2017, 7, 158. [Google Scholar] [CrossRef] [Green Version]
- Hosseininejad, S.E.; Neshat, M.; Faraji-Dana, R.; Lemme, M.; Bolívar, P.H.; Cabellos-Aparicio, A.; Alarcón, E.; Abadal, S. Reconfigurable THz plasmonic antenna based on few-layer graphene with high radiation efficiency. Nanomaterials 2018, 8, 577. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Ren, G.; Zhu, B.; Liu, H.; Lian, Y.; Jian, S. Analytical model for plasmon modes in graphene-coated nanowire. Opt. Express 2014, 22, 24322–24331. [Google Scholar] [CrossRef]
- Gao, Y.; Ren, G.; Zhu, B.; Wang, J.; Jian, S. Single-mode graphene-coated nanowire plasmonic waveguide. Opt. Lett. 2014, 39, 5909–5912. [Google Scholar] [CrossRef] [PubMed]
- Kuzmin, D.A.; Bychkov, I.V.; Shavrov, V.G.; Temnov, V.V.; Lee, H.I.; Mok, J. Plasmonically induced magnetic field in graphene-coated nanowires. Opt. Lett. 2016, 41, 396–399. [Google Scholar] [CrossRef] [PubMed]
- Teng, D.; Wang, K.; Li, Z.; Zhao, Y. Graphene-coated nanowire dimers for deep subwavelength waveguiding in mid-infrared range. Opt. Express 2019, 27, 12458–12469. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, L.; Yin, H.; Zhang, M.; Su, H.; Li, I.L.; Liang, H. Graphene-coated nanowires with a drop-shaped cross section for 10 nm confinement and 1 mm propagation. Opt. Lett. 2017, 42, 2078–2081. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.P.; Zhai, X.; Wang, L.L.; Li, H.J.; Xie, F.; Lin, Q.; Xia, S.X. Analysis of mid-infrared surface plasmon modes in a graphene-based cylindrical hybrid waveguide. Plasmonics 2016, 11, 703–711. [Google Scholar] [CrossRef]
- Heydari, M.B.; Samiei, M.H.V. Plasmonic graphene waveguides: A literature review. arXiv 2018, arXiv:1809.09937. [Google Scholar]
- Zhang, Q.; Li, X.; Hossain, M.M.; Xue, Y.; Zhang, J.; Song, J.; Liu, J.; Turner, M.D.; Fan, S.; Bao, Q.; et al. Graphene surface plasmons at the near-infrared optical regime. Sci. Rep. 2014, 4, 6559. [Google Scholar] [CrossRef]
- Cao, K.; Feng, S.; Han, Y.; Gao, L.; Ly, T.H.; Xu, Z.; Lu, Y. Elastic straining of free-standing monolayer graphene. Nat. Commun. 2020, 11, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Guo, M.; Qian, Y.; Qi, H.; Bi, K.; Chen, Y. Experimental measurements on the thermal conductivity of strained monolayer graphene. Carbon 2020, 157, 185–190. [Google Scholar] [CrossRef]
- Jabbarzadeh, F.; Heydari, M.; Habibzadeh-Sharif, A. A comparative analysis of the accuracy of Kubo formulations for graphene plasmonics. Mater. Res. Exp. 2019, 6, 086209. [Google Scholar] [CrossRef]
- Oulton, R.F.; Sorger, V.J.; Genov, D.A.; Pile, D.F.P.; Zhang, X. A hybrid plasmonic waveguide for subwavelength confinement and long-range propagation. Nat. Photonics 2008, 2, 496–500. [Google Scholar] [CrossRef] [Green Version]
- Buckley, R.; Berini, P. Figures of merit for 2D surface plasmon waveguides and application to metal stripes. Opt. Express 2007, 15, 12174–12182. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Yao, J.; Xu, W. Terahertz photonic states in semiconductor–graphene cylinder structures. Opt. Lett. 2012, 37, 960–962. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Liu, X.; Qiu, W.; Ma, Y.; Huang, Y.; Wang, J.-X.; Qiang, K.; Pan, J.-Q. Surface-plasmon-polariton whispering-gallery mode analysis of the graphene monolayer coated InGaAs nanowire cavity. Opt. Express 2014, 22, 5754–5761. [Google Scholar] [CrossRef] [PubMed]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Alvarez-Melcon, A. Surface plasmons in graphene cylindrical waveguides. In Proceedings of the 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI), Memphis, TN, USA, 6–11 July 2014. [Google Scholar]
- Cao, T.; Tian, L.; Liang, H.; Qin, K.-R. Reconfigurable, graphene-coated, chalcogenide nanowires with a sub-10-nm enantioselective sorting capability. Microsyst. Nanoeng. 2018, 4, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, B.; Meng, C.; Yang, Z.; Li, W.; Lin, S.; Gu, T.; Guo, X.; Wang, D.; Yu, S.; Wong, C.W.; et al. Graphene coated ZnO nanowire optical waveguides. Opt. Express 2014, 22, 24276–24285. [Google Scholar] [CrossRef]
- He, X.; Zhang, X.; Zhang, H.; Xu, M. Graphene covered on microfiber exhibiting polarization and polarization-dependent saturable absorption. IEEE J. Sel. Top. Quant. 2014, 20, 55–61. [Google Scholar]
- Zhu, B.; Ren, G.; Gao, Y.; Yang, Y.; Lian, Y.; Jian, S. Graphene-coated tapered nanowire infrared probe: A comparison with metal-coated probes. Opt. Express 2014, 22, 24096–24103. [Google Scholar] [CrossRef]
- Stockman, M.I. Nanofocusing of optical energy in tapered plasmonic waveguides. Phys. Rev. Lett. 2004, 93, 137404. [Google Scholar] [CrossRef] [Green Version]
- Zhu, B.; Ren, G.; Gao, Y.; Yang, Y.; Wu, B.; Lian, Y.; Jian, S. Nanofocusing in the graphene-coated tapered nanowire infrared probe. J. Opt. Soc. Am. B 2015, 32, 955–960. [Google Scholar] [CrossRef]
- Davoyan, A.R.; Engheta, N. Salient features of deeply subwavelength guiding of terahertz radiation in graphene-coated fibers. ACS Photonics 2016, 3, 737–742. [Google Scholar] [CrossRef]
- Cong, X.; Huang, Y.; Zhang, M.; Su, H.; Li, I.L.; Liang, H. Graphene-coated nanowires with drop-shaped cross section for the low loss propagation of THz waves with sub-micron mode widths. Laser Phys. Lett. 2018, 15, 096001. [Google Scholar] [CrossRef]
- Teng, D.; Wang, K.; Li, Z.; Zhao, Y.; Zhao, G.; Li, H.; Wang, H. Graphene-coated elliptical nanowires for low loss subwavelength terahertz transmission. Appl. Sci. 2019, 9, 2351. [Google Scholar] [CrossRef] [Green Version]
- Cheng, X.; Xue, W.-R.; Wei, Z.-Z.; Dong, H.-Y.; Li, C.-Y. Mode characteristic analysis of optical waveguides based on graphene-coated elliptical dielectric nanowire. Acta Phys. Sin. 2019, 68, 058101. [Google Scholar]
- Wu, Z.; Ning, T.; Li, J.; Zhang, M.; Su, H.; Li, I.L.; Liang, H. Tunable photonic-like modes in graphene-coated nanowires. Opt. Express 2019, 27, 35238–35244. [Google Scholar] [CrossRef] [PubMed]
- Cuevas, M.; Riso, M.A.; Depine, R.A. Complex frequencies and field distributions of localized surface plasmon modes in graphene-coated subwavelength wires. J. Quant. Spectrosc. Radiat. Transf. 2016, 173, 26–33. [Google Scholar] [CrossRef]
- Kuzmin, D.A.; Bychkov, I.V.; Shavrov, V.G.; Kotov, L.N. Transverse-electric plasmonic modes of cylindrical graphene-based waveguide at near-infrared and visible frequencies. Sci. Rep. 2016, 6, 26915. [Google Scholar] [CrossRef]
- Liu, J.-P.; Zhai, X.; Xie, F.; Wang, L.-L.; Xia, S.-X.; Li, H.-J.; Luo, X.; Shang, X.-J. Analytical model of mid-infrared surface plasmon modes in a cylindrical long-range waveguide with double-layer graphene. J. Light. Technol. 2017, 35, 1971–1979. [Google Scholar] [CrossRef]
- Zhao, T.; Hu, M.; Zhong, R.; Chen, X.; Zhang, P.; Gong, S.; Zhang, C.; Liu, S. Plasmon modes of circular cylindrical double-layer graphene. Opt. Exp. 2016, 24, 20461–20471. [Google Scholar] [CrossRef]
- Cheng, X.; Xue, W.R.; Wei, Z.Z.; Dong, H.Y.; Li, C.Y. Mode analysis of a confocal elliptical dielectric nanowire coated with double-layer graphene. Opt. Commun. 2019, 452, 467–475. [Google Scholar] [CrossRef]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Alu, A.; Alvarez-Melcon, A. Electrically and magnetically biased graphene-based cylindrical waveguides: Analysis and applications as reconfigurable antennas. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 951–960. [Google Scholar] [CrossRef]
- Mbonye, M.; Mendis, R.; Mittleman, D.M. A terahertz two-wire waveguide with low bending loss. Appl. Phys. Lett. 2009, 95, 233506. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Cao, Q.; Teng, D.; Zhu, M.; Wang, K. Perturbative solution for terahertz two-wire metallic waveguides with different radii. Opt. Express 2015, 23, 27457–27473. [Google Scholar] [CrossRef] [PubMed]
- Zhu, B.; Ren, G.; Yang, Y.; Gao, Y.; Wu, B.; Lian, Y.; Wang, J.; Jian, S. Field enhancement and gradient force in the graphene-coated nanowire pairs. Plasmonics 2015, 10, 839–845. [Google Scholar] [CrossRef]
- Zhai, L.; Xue, W.; Yang, R.; Han, L. Propagation properties of nano dielectric parallel lines coated with graphene. Acta Opt. Sin. 2015, 35, 1123002. [Google Scholar] [CrossRef]
- Peng, Y.-L.; Xue, W.-R.; Wei, Z.-Z.; Li, C.-Y. Mode properties analysis of graphene-coated asymmetric parallel dielectric nanowire waveguides. Acta Phys. Sin. 2018, 67, 038102. [Google Scholar]
- Wu, D.; Tian, J. Study on the plasmonic characteristics of bow-tie type graphene-coated nanowire pair. Optik 2018, 156, 689–695. [Google Scholar] [CrossRef]
- Teng, D.; Wang, K.; Huan, Q.; Zhao, Y.; Tang, Y. High-performance transmission of surface plasmons in graphene-covered nanowire pairs with substrate. Nanomaterials 2019, 9, 1594. [Google Scholar] [CrossRef] [Green Version]
- Raad, S.H.; Atlasbaf, Z.; Zapata-Rodríguez, C.J. Multi-frequency near-field enhancement with graphene-coated nano-disk homo-dimers. Opt. Express 2019, 27, 37012–37024. [Google Scholar] [CrossRef]
- Kim, J.T.; Yu, Y.-J.; Choi, H.; Choi, C.-G. Graphene-based plasmonic photodetector for photonic integrated circuits. Opt. Express 2014, 22, 803–808. [Google Scholar] [CrossRef]
- Hajati, M.; Hajati, Y. High-performance and low-loss plasmon waveguiding in graphene-coated nanowire with substrate. J. Opt. Soc. Am. B 2016, 33, 2560–2565. [Google Scholar] [CrossRef]
- Hajati, M.; Hajati, Y. Plasmonic Characteristics of two vertically coupled graphene-coated nanowires integrated with substrate. Appl. Opt. 2017, 56, 870–875. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Tian, J.; Yang, R. Study of mode performances of graphene-coated nanowire integrated with triangle wedge substrate. J. Nonlinear Opt. Phys. Mater. 2018, 27, 1850013. [Google Scholar] [CrossRef]
- Sun, M.; Tian, J.; Lan, X.; He, Z.; Liu, J. Transmission properties of two vertically coupled double-graphene-coated nanowires integrated with substrate. Optik 2019, 185, 242–247. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Liu, D.; Xia, X. Active manipulating propagation in the graphene hybrid plasmonic waveguides in mid-infrared region. In Electro-Optical and Infrared Systems: Technology and Applications XIII; SPIE: Edinburgh, UK, 2016. [Google Scholar]
- Zhou, X.; Zhang, T.; Chen, L.; Hong, W.; Li, X. A graphene-based hybrid plasmonic waveguide with ultra-deep subwavelength confinement. J. Light. Technol. 2014, 32, 4199–4203. [Google Scholar] [CrossRef]
- Liu, J.-P.; Zhai, X.; Wang, L.-L.; Li, H.-J.; Xie, F.; Xia, S.-X.; Shang, X.-J.; Luo, X. Graphene-based long-range SPP hybrid waveguide with ultra-long propagation length in mid-infrared range. Opt. Express 2016, 24, 5376–5386. [Google Scholar] [CrossRef]
- Chen, M.; Sheng, P.; Sun, W.; Cai, J. A symmetric terahertz graphene-based hybrid plasmonic waveguide. Opt. Commun. 2016, 376, 41–46. [Google Scholar] [CrossRef]
- Ye, L.; Sui, K.; Liu, Y.; Zhang, M.; Liu, Q.H. Graphene-based hybrid plasmonic waveguide for highly efficient broadband mid-infrared propagation and modulation. Opt. Express 2018, 26, 15935–15947. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Liu, H.; Wang, S.; Cai, M.; Ma, L. Optical transport properties of graphene surface plasmon polaritons in mid-infrared band. Crystals 2019, 9, 354. [Google Scholar] [CrossRef] [Green Version]
- Cui, J.; Sun, Y.; Wang, L.; Ma, P. Graphene plasmonic waveguide based on a high-index dielectric wedge for compact photonic integration. Optik 2016, 127, 152–155. [Google Scholar] [CrossRef]
- He, X.; Ning, T.; Lu, S.; Zheng, J.; Li, J.; Li, R.; Pei, L. Ultralow loss graphene-based hybrid plasmonic waveguide with deep-subwavelength confinement. Opt. Express 2018, 26, 10109–10118. [Google Scholar] [CrossRef] [PubMed]
- He, X.Q.; Ning, T.G.; Pei, L.; Zheng, J.J.; Li, J.; Wen, X.D. Tunable hybridization of graphene plasmons and dielectric modes for highly confined light transmit at terahertz wavelength. Opt. Express 2019, 27, 5961–5972. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Ning, T.; Zheng, J.; Li, J.; Pei, L.; Wu, B. Deep-subwavelength light transmission in hybrid graphene-dielectric slot waveguide. J. Opt. 2019, 21, 095001. [Google Scholar] [CrossRef]
- Wan, P.; Yang, C.; Liu, Z. Channel hybrid plasmonic modes in dielectric-loaded graphene groove waveguides. Opt. Commun. 2018, 420, 72–77. [Google Scholar] [CrossRef]
- Molina, M.I.; Kivshar, Y.S. Discrete and surface solitons in photonic graphene nanoribbons. Opt. Lett. 2010, 35, 2895–2897. [Google Scholar] [CrossRef] [Green Version]
- Kou, Y.; Förstner, J. Discrete plasmonic solitons in graphene-coated nanowire arrays. Opt. Express 2016, 24, 4714–4721. [Google Scholar] [CrossRef] [Green Version]
- Meng, P.; Zhao, D.; Zhong, D.; Liu, W. Topological plasmonic modes in graphene-coated nanowire arrays. Opt. Quant. Electron. 2019, 51, 156. [Google Scholar] [CrossRef]
- Wei, Z.-Z.; Xue, W.-R.; Peng, Y.-L.; Cheng, X.; Li, C.-Y. Mode characteristics of waveguides based on three graphene-coated dielectric nanowires. Acta Opt. Sin. 2019, 39, 0124001. [Google Scholar]
- Wei, Z.-Z.; Xue, W.-R.; Peng, Y.-L.; Cheng, X.; Li, C.-Y. Modes characteristics analysis of THz waveguides based on three graphene-coated dielectric nanowires. Acta Phys. Sin. 2018, 67, 108101. [Google Scholar]
- Ghaemi, H.F.; Thio, T.; Grupp, D.E.; Ebbesen, T.W.; Lezec, H.J. Surface plasmons enhance optical transmission through subwavelength holes. Phys. Rev. B 1998, 58, 6779–6782. [Google Scholar] [CrossRef] [Green Version]
- Cao, Q.; Lalanne, P. Negative role of surface plasmons in the transmission of metallic gratings with very narrow slits. Phys. Rev. Lett. 2002, 88, 057403. [Google Scholar] [CrossRef] [Green Version]
- Fei, Z.; Rodin, A.S.; Andreev, G.O.; Bao, W.; McLeod, A.S.; Wagner, M.; Zhang, L.M.; Zhao, Z.; Thiemens, M.; Dominguez, G.; et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 2012, 487, 82–85. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Badioli, M.; Alonso-González, P.; Thongrattanasiri, S.; Huth, F.; Osmond, J.; Spasenović, M.; Centeno, A.; Pesquera, A.; Godignon, P.; et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 2012, 487, 77–81. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, W.; Shu, J.; Qiu, C.; Xu, Q. Excitation of plasmonic waves in graphene by guided-mode resonances. ACS Nano 2012, 6, 7806–7813. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.; Dong, Z.; Yang, J.K.W.; Wang, Q.J. Plasmon excitation on flat graphene by s-polarized beams using four-wave mixing. Opt. Express 2015, 23, 7809–7819. [Google Scholar] [CrossRef]
- Nikitin, A.Y.; Alonso-González, P.; Hillenbrand, R. Efficient coupling of light to graphene plasmons by compressing surface polaritons with tapered bulk materials. Nano Lett. 2014, 14, 2896–2901. [Google Scholar] [CrossRef] [Green Version]
- Xia, S.-X.; Zhai, X.; Wang, L.-L.; Liu, J.-P.; Li, H.-J.; Liu, J.-Q.; Pan, A.-L.; Wen, S.-C. Excitation of surface plasmons in graphene-coated nanowire arrays. J. Appl. Phys. 2016, 120, 103104. [Google Scholar] [CrossRef]
- Asgari, S.; Kashani, Z.G.; Granpayeh, N. Tunable nano-scale graphene-based devices in mid-infrared wavelengths composed of cylindrical resonators. J. Opt. 2018, 20, 045001. [Google Scholar] [CrossRef]
- Cao, T.; Li, Y.; Tian, L.; Liang, H.; Qin, K. Fast switching “on/off“ chiral surface plasmon polaritons in graphene-coated Ge2Sb2Te5 nanowire. ACS Appl. Nano Mater. 2018, 1, 759–767. [Google Scholar] [CrossRef]
- Gan, X.; Zhao, C.; Wang, Y.; Mao, D.; Fang, L.; Han, L.; Zhao, J. Graphene-assisted all-fiber phase shifter and switching. Optica 2015, 2, 468–471. [Google Scholar] [CrossRef]
- Jalas, D.; Petrov, A.; Eich, M.; Freude, W.; Fan, S.; Yu, Z.; Baets, R.; Popović, M.; Melloni, A.; Joannopoulos, J.D.; et al. What is—And what is not—An optical isolator. Nat. Photonics 2013, 7, 579–582. [Google Scholar] [CrossRef]
- Pae, J.-S.; Im, S.-J.; Ri, C.-S.; Ho, K.-S.; Song, G.-S.; Han, Y.-H.; Herrmann, J. Magnetoplasmonic isolators based on graphene waveguide ring resonators. Phys. Rev. B 2019, 100, 041405. [Google Scholar] [CrossRef]
- Kou, J.; Chen, J.; Chen, Y.; Xu, F.; Lu, Y. Platform for enhanced light–graphene interaction length and miniaturizing fiber stereo devices. Optica 2014, 1, 307–310. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Yin, X.; Ulin-Avila, E.; Geng, B.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef]
- Li, W.; Chen, B.; Meng, C.; Fang, W.; Xiao, Y.; Li, X.; Hu, Z.; Xu, Y.; Tong, L.; Wang, H.; et al. Ultrafast all-optical graphene modulator. Nano Lett. 2014, 14, 955–959. [Google Scholar] [CrossRef]
- Chen, J.-H.; Zheng, B.-C.; Shao, G.-H.; Ge, S.-J.; Xu, F.; Lu, Y.-Q. An all-optical modulator based on a stereo graphene–microfiber structure. Light Sci. Appl. 2015, 4, e360. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, L.; Zhang, S.; Cao, T.; Alù, A.; Ruan, S.; Qiu, C.-W. Gate-programmable electro-optical addressing array of graphene-coated nanowires with sub-10 nm resolution. ACS Photonics 2016, 3, 1847–1853. [Google Scholar] [CrossRef]
- He, X.; Liu, Z.-B.; Wang, D.; Yang, M.; Liao, C.R.; Zhao, X. Passively mode-locked fiber laser based on reduced graphene oxide on microfiber for ultra-wide-band doublet pulse generation. J. Light. Technol. 2012, 30, 984–989. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, M.; Liu, H.; Zheng, X.-W.; Ning, Q.-Y.; Luo, A.-P.; Luo, Z.-C.; Xu, W.-C. Dual-wavelength rectangular pulse Yb-doped fiber laser using a microfiber-based graphene saturable absorber. Opt. Express 2014, 22, 10906–10913. [Google Scholar] [CrossRef]
- Liu, X.M.; Yang, H.R.; Cui, Y.D.; Chen, G.W.; Yang, Y.; Wu, X.Q.; Yao, X.K.; Han, D.D.; Han, X.X.; Zeng, C.; et al. Graphene-clad microfibre saturable absorber for ultrafast fibre lasers. Sci. Rep. 2016, 6, 26024. [Google Scholar] [CrossRef] [Green Version]
- Yao, B.C.; Rao, Y.J.; Huang, S.W.; Wu, Y.; Feng, Z.Y.; Choi, C.; Liu, H.; Qi, H.F.; Duan, X.F.; Peng, G.D.; et al. Graphene Q-switched distributed feedback fiber lasers with narrow linewidth approaching the transform limit. Opt. Express 2017, 25, 8202–8211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.-F.; Zhang, J.-H.; Peng, X.-L.; Mao, X.-F. Generation and evolution of multiple operation states in passively mode-locked thulium-doped fiber laser by using a graphene-covered-microfiber. Chin. Phys. B 2018, 27, 084215. [Google Scholar] [CrossRef]
- Li, D.; Zhu, J.; Jiang, M.; Li, D.; Wu, H.; Han, J.; Sun, Z.; Ren, Z. Active–passive Q-switched fiber laser based on graphene microfiber. Appl. Phys. B 2019, 125, 203. [Google Scholar] [CrossRef]
- Almeida, V.R.; Lipson, M. Optical bistability on a silicon chip. Opt. Lett. 2004, 29, 2387–2389. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Wang, H.; Zheng, B.; Dehdashti, S.; Li, E.; Chen, H. Bistable scattering in graphene-coated dielectric nanowires. Nanoscale 2017, 9, 8449–8457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, K.; Gao, L. Optical bistability in graphene-wrapped dielectric nanowires. Opt. Express 2017, 25, 13747–13759. [Google Scholar] [CrossRef]
- Feng, Q.-Y.; Yao, B.-C.; Zhou, J.-H.; Xia, H.-D.; Fan, M.-Q.; Zhang, L.; Wu, Y.; Rao, Y.-J. Four-wave-mixing generated by femto-second laser pumping based on graphene coated microfiber structure. Acta Phys. Sin. 2015, 64, 184214. [Google Scholar]
- Gao, Y.; Shadrivov, I.V. Second harmonic generation in graphene-coated nanowires. Opt. Lett. 2016, 41, 3623–3626. [Google Scholar] [CrossRef]
- Gao, Y.; Shadrivov, I.V. Nonlinear coupling in graphene-coated nanowires. Sci. Rep. 2016, 6, 38924. [Google Scholar] [CrossRef]
- Kuzmin, D.A.; Bychkov, I.V.; Shavrov, V.G.; Temnov, V.V. Giant faraday rotation of high-order plasmonic modes in graphene-covered nanowires. Nano Lett. 2016, 16, 4391–4395. [Google Scholar] [CrossRef] [Green Version]
- Cai, W.; Chettiar, U.K.; Kildishev, A.V.; Shalaev, V.M. Optical cloaking with metamaterials. Nat. Photonics 2007, 1, 224–227. [Google Scholar] [CrossRef] [Green Version]
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chan, C.T.; Sheng, P. Transformation optics and metamaterials. Nat. Mater. 2010, 9, 387–396. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.-Y.; Alù, A. Atomically thin surface cloak using graphene monolayers. ACS Nano 2011, 5, 5855–5863. [Google Scholar] [CrossRef]
- Naserpour, M.; Zapata-Rodríguez, C.J.; Vuković, S.M.; Pashaeiadl, H.; Belić, M.R. Tunable invisibility cloaking by using isolated graphene-coated nanowires and dimers. Sci. Rep. 2017, 7, 12186. [Google Scholar] [CrossRef]
- Fesenko, V.I.; Shcherbinin, V.I.; Tuz, V.R. Multiple invisibility regions induced by symmetry breaking in a trimer of subwavelength graphene-coated nanowires. J. Opt. Soc. Am. A 2018, 35, 1760–1768. [Google Scholar] [CrossRef]
- Shcherbinin, V.I.; Moskvitina, Y.K.; Fesenko, V.I.; Tuz, V.R. Dual-polarized all-angle cloaking of a dielectric nanowire by helical graphene ribbons. Phys. Rev. B 2019, 100, 035428. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Zhang, D.; Zhang, B.; Luo, Y. Interaction between graphene-coated nanowires revisited with transformation optics. Opt. Lett. 2017, 42, 2890–2893. [Google Scholar] [CrossRef]
- Yang, Y.; Shi, Z.; Li, J.; Li, Z.-Y. Optical forces exerted on a graphene-coated dielectric particle by a focused Gaussian beam. Photon. Res. 2016, 4, 65–69. [Google Scholar] [CrossRef]
- Wei, B.; Jian, S. Multiple modes plasmon-induced-transparency and slow light effect in a compact graphene coated nanowire waveguide system. Opt. Commun. 2017, 402, 66–72. [Google Scholar] [CrossRef]
- Arruda, T.J.; Bachelard, R.; Weiner, J.; Courteille, P.W. Tunable Fano resonances in the decay rates of a pointlike emitter near a graphene-coated nanowire. Phys. Rev. B 2018, 98, 245419. [Google Scholar] [CrossRef] [Green Version]
- Olivo, J.; Cuevas, M. Enhanced energy transfer via graphene–coated wire surface plasmons. J. Quant. Spectrosc. Radiat. Transf. 2019, 239, 106655. [Google Scholar] [CrossRef] [Green Version]













© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, D.; Wang, K.; Li, Z. Graphene-Coated Nanowire Waveguides and Their Applications. Nanomaterials 2020, 10, 229. https://doi.org/10.3390/nano10020229
Teng D, Wang K, Li Z. Graphene-Coated Nanowire Waveguides and Their Applications. Nanomaterials. 2020; 10(2):229. https://doi.org/10.3390/nano10020229
Chicago/Turabian StyleTeng, Da, Kai Wang, and Zhe Li. 2020. "Graphene-Coated Nanowire Waveguides and Their Applications" Nanomaterials 10, no. 2: 229. https://doi.org/10.3390/nano10020229
APA StyleTeng, D., Wang, K., & Li, Z. (2020). Graphene-Coated Nanowire Waveguides and Their Applications. Nanomaterials, 10(2), 229. https://doi.org/10.3390/nano10020229