1. Introduction
The widespread application of nanoporous materials in several fields, such as chromatography, membrane separation, catalysis, etc., has lead to a growing interest in the accurate description of the thermodynamic behavior of fluids confined in nanopores [
1,
2,
3,
4,
5,
6]. The pressure of a nanoconfined fluid is one of the most important thermodynamic properties which is needed for an accurate description of the flow rate, diffusion coefficient, and the swelling of the nanoporous material [
7,
8,
9,
10]. Various approaches for calculating the pressure of a fluid in a nanopore have been proposed [
1,
11,
12,
13]. The main difficulty of the pressure calculation arises from the ambiguous definition of the pressure tensor inside porous materials due to the presence of curved surfaces and confinement effects [
7,
14,
15]. Traditional thermodynamic laws and concepts, such as Gibbs surface dynamics, Kelvin equation, etc., may not be applicable at the nano-scale [
16]. In the past decade, several methods were reported using different simulation techniques i.e., classical density functional theory [
17,
18], equation of state modeling [
19], etc., to model the behavior of fluids in confinement.
Recently, Galteland et al. [
11] reported a new approach for the calculation of pressure in nanoporous materials using Hill’s thermodynamics for small systems [
20]. In this approach, two different pressures are needed to account for confinement effects in nanoporous materials: the differential pressure
P, and the integral pressure
. In an ensemble of small systems, the differential pressure times the volume change of the small systems is equal to the work exerted on the surroundings by the volume change. The differential pressure corresponds to the macroscopic pressure and does not depend on the size of the system. The addition of a small system to an ensemble of small systems exerts work on the surroundings which is equal to the integral pressure times the volume of the added small system. The differential and integral pressures are different for small systems and become equal in the thermodynamic limit. For a system with volume
V, the two pressures are related by [
11,
20]:
As shown in Equation (
1), the two pressures are different only when the integral pressure
depends on the volume of the system. Galteland et al. [
11] performed equilibrium and non-equilibrium molecular dynamics simulations of Lennard–Jones (LJ) fluids in a face-centered lattice of spherical grains representing a porous medium. Using Hill’s thermodynamics of small systems [
20] and the additive property of the grand potential, Galteland et al. [
11] defines the compressional energy (
) of the representative elementary volume (REV) in the simulations as follows:
where
is the integral pressure of volume V,
and
are the integral pressure and volume of the fluid,
and
are the integral pressure and volume of the grain particles, and the
and
are the integral surface tension and surface area between the fluid and grain particles. Based on the obtained results, it was concluded that the definition of two pressures is needed to calculate the pressure of the fluid in nanoporous medium.
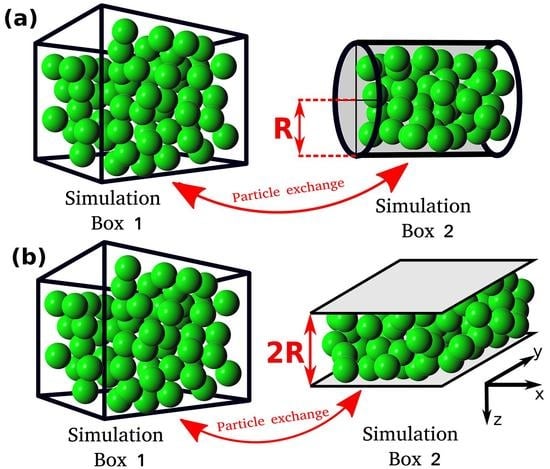
In this study, the relation between the differential and integral pressure is investigated by performing Monte Carlo (MC) simulations of LJ fluids. The simulations are carried out in a modified Gibbs ensemble, using two simulation boxes in equilibrium with each other. One box represents the bulk fluid, while the other simulation box represents the nanoconfined system, including walls that interact with the fluid particles, as shown in
Figure 1. The effect of confinement on the integral pressure is investigated by considering different fluid-wall interaction strengths and pore geometries, namely, a cylinder and a slit pore. To investigate the relation between the differential and integral pressure, the difference of the two pressures,
, and the ratio of driving forces for mass transport,
, are computed. In
Section 2, the devised ensemble and the equations used to calculate the pressure and energy of the system are presented. In
Section 3, a rigorous derivation of the used expression to compute the ratio of driving forces is shown. In
Section 4, the results for the different differential pressures and pore geometries are shown. In
Section 5, our conclusions are summarized.
2. Simulation Details
All MC simulations are carried out using an in-house simulation code. The MC simulations consist of two simulation domains, Simulation Box 1 and Simulation box 2 (see
Figure 1). Throughout the manuscript the terms Simulation Box 1 and 2 are used to refer to the two domains, however, simulation domain 2 does not correspond to an actual box. The total number of particles in the system,
, is fixed and particles can be exchanged between the simulation boxes. Box 1 is cubic and has periodic boundary conditions imposed in all directions. Box 1 represents a bulk fluid. The differential pressure,
P, and temperature,
T, in Simulation Box 1 are imposed, while the volume,
, and the number of particles,
, can fluctuate. Simulation Box 2 is a cylinder or a slit pore with a fixed volume
. The size of the cylinder and the slit pore are defined by the radius,
R, and by the distance between the two parallel planes,
, respectively (
Figure 1). In Box 2, periodic boundary conditions are applied only in the axial direction for the cylinder and in the x and y directions for the slit pore (see
Figure 1). Box 2 represents the confined fluid which has an integral pressure
. In Simulation Box 2, the volume,
, and temperature
T are imposed, while the number of particles
can fluctuate by exchanging particles with Box 1. The instantaneous integral pressure fluctuates, and by definition [
20] its ensemble average,
, will be equal to
P only for macroscopic systems (
). The ensemble used is a variation of the
-Gibbs ensemble [
21]. The main difference between the ensemble used in this work and the conventional
-Gibbs ensemble is that in our simulations the volume of Box 2 is fixed [
21]. Essentially, Box 2 corresponds to the grand canonical ensemble with the reservoir explicitly modeled in Box 1. This computational setup was also used in other studies, i.e., A. Z. Panagiotopoulos et al. [
21], P. Bai et al. [
22], etc.
In the MC simulations, three types of trial moves are used: translation, volume change, and particle exchange. The translation and particle exchange trial moves are used in both simulation boxes, while volume change trial moves are only performed in Simulation Box 1. The acceptance rules of the trial moves can be found elsewhere [
23]. The particle exchange trial move, ensures that Box 1 and Box 2 are in chemical equilibrium, i.e., the chemical potentials of the two boxes are equal (
). The chemical potentials of the boxes are defined as the sum of the ideal and excess chemical potentials of the fluid in the respective box (
). The ideal gas chemical potentials (
) are calculated based on the density and temperature of the fluid. The excess chemical potential (
) can be calculated using different methods, i.e., Widom’s test particle insertion method [
23], Contionous Fractional Component Monte Carlo method [
24,
25], Bennet acceptance ratio method [
26], etc. Although the Bennet acceptance ratio method is computationally more efficient than the Widom’s test particle insertion method, the Widom’s test particle method is sufficient for the systems considered in this study. Separate simulations are carried out using different cylinder radii
R, while imposing
(in reduced units) in Box 1. In
Figure 2, the chemical potential of Box 1 and Box 2 (
Figure 2a), as well as the density of Box 1 and Box 2 (
Figure 2b), are shown as a function of the cylinder radius at
. As can be seen from
Figure 2a, the chemical potentials of Box 1 and Box 2 are equal within the uncertainties of the simulations.
In all simulations, the total potential energy,
U, is calculated using the 12-6 LJ interaction potential:
where
is the potential energy due to interaction between the fluid particles, and
represents the potential energy contribution from the interactions between the fluid particles and the wall of Box 2.
in both simulation boxes is calculated according to:
where
is the distance of particle
i and
j,
makes the interaction potentially continuous at the cut-off distance (
), and
,
are the LJ parameters. In the past, several studies were reported using different types of interaction potentials to model the fluid-solid interactions in confined spaces [
22,
27,
28]. Since the aim of this study is to show the difference between the differential and integral pressures and not to simulate some specific adsorption system, only two types of interaction potentials are considered for the interaction of fluid particles with the wall in Simulation Box 2. In the first case, the wall has only repulsive interactions with the fluid particles. The potential energy contribution of this type is calculated based on the Weeks–Chandler–Andersen potential [
29]:
where
is the number of particles in Box 2,
is the closest distance of particle
i from the walls, and
and
are the LJ parameters for the interaction between the wall and the fluid particles. In the second case, the attractive interactions between the wall and fluid particles are taken into account using the traditional form of the 12-6 LJ interaction potential:
where
makes the interaction potential continuous at the cut-off distance, and
and
are the LJ parameters.
The expression for calculating the integral pressure in Box 2 is as follows [
30]:
where
represents the contribution of the fluid-fluid interaction to the integral pressure,
is the Boltzmann constant, and
represents the contribution of the fluid-wall interaction to the integral pressure. The
, and
terms represent the virial contributions of the integral pressure. The terms are calculated based on the virial theorem [
7], i.e., using the derivative of the potential energy function with respect to
r. The pressure term
is calculated as follows [
7]:
The third term in Equation (
7) represents the pressure contribution related to the interactions of the LJ particles with the wall of Box 2. The term
for the repulsive wall potential is derived based on Equation (
5) [
7]. The following expression is obtained:
The following expression is used to calculate the
when the wall has also attractive interactions with the fluid [
7]:
By comparing Equations (
8)–(
10), it can observed that the multiplication factor 48 in Equation (
8) is replaced by the factor 24 in Equations (
9) and (
10). This difference means that only 50 % of the fluid-wall interactions are taken into account at the calculation of the
term [
7]. In the MC simulations, Equations (
7)–(
10) yield instantaneous values from which ensemble averages are computed, i.e.,
.
In all simulations, the LJ parameters of the fluid particles are
,
, and the cut-off radius is
for the fluid-fluid interactions. Regardless of the type of interaction potential used to calculate the interaction of the fluid particles and the wall in Simulation Box 2, the LJ parameter,
is used. In the case of the purely repulsive wall potential, the LJ parameter
is used. In case of the attractive wall potential, five different values for the
LJ parameters are considered:
. In this study, all of the reported parameters are in dimensionless units. The LJ interactions are truncated and shifted (i.e., no tail corrections are applied). To avoid phase transitions, the temperature is fixed at
[
31,
32].
3. Theory
To investigate the difference between the differential and integral pressures, the ratio
is calculated. The term
is the ratio of the pressure gradient for mass transport in the bulk phase,
, and in the confined space
(see
Figure 3). Essentially, the ratio of driving forces,
, equals the ratio of transport coefficients when either
P or
is used as driving force for mass transport in the corresponding transport equation.
is referred to as the ratio of driving forces throughout this work. One possible approach to compute the ratio of driving forces is to perform simulations at different imposed differential pressures and calculate the difference in the differential and integral pressures. To avoid the necessity of performing several simulations, in this study the ratio of driving forces is calculated based on the fluctuation theory. Using this approach, the ratio of driving forces can be obtained by performing a single simulation.
To obtain an expression for
, the partition function of the system is needed [
23]:
where C is a constant,
,
is the number of particles in Box 1,
is total number of particles in the simulation,
is the volume of Box 1,
is the volume of Box 2, and
U is the potential energy. The ensemble average of a thermodynamic property
X can be obtained using:
Therefore, to obtain the expression for
, the following relation is used:
By switching the order of the integration and differentiation, the following expression is obtained:
The final expression in Equation (
14) is essentially the cross correlation between
and
. In this study, this expression is used to calculate the ratio of driving forces.
5. Conclusions
In this study, the new approach reported by Galteland et al. [
11] is used to investigate the effects of confinement on a fluid in a nanopore by performing MC simulations. The simulations are carried out in a variation of the Gibbs ensemble with two simulation boxes in chemical equilibrium. One of the simulation boxes represents the bulk fluid with differential pressure
P, and the other a slit or cylindrical pore with repulsive or attractive wall interaction potential. In case of the attractive wall potentials, several scenarios are considered for the strength of the interaction between the wall and the fluid particles. The effect of confinement is investigated for three differential pressures,
0.2, 2.0, 6.0, corresponding to gas (
) and liquid phases (
). It is concluded that the difference between the differential and integral pressure
, for all studied cases, approaches 0 when
R→∞. It is shown that the increase in the interaction strength between the wall and the fluid particles has smaller effect on the difference in the pressures,
, as the differential pressure increases. Based on the work of Galteland et al. [
11], the difference of the differential and integral pressure is related to the effective surface tension between the fluid particles and wall of the pore. It is shown that the effective surface tension does not depend on the curvature of the wall. It is found that by considering a bulk fluid in equilibrium with a cylindrical or slit nanopore, the ratio of driving forces for mass transport in the bulk phase is larger than in the nanopore (
) for small pore sizes. As
R increases,
approaches 1, i.e., the fluid in the pore behaves more like a bulk fluid. This clearly shows that the approximation that
does not hold on the nanoscale.